一维PT对称非厄米自旋轨道耦合Su-Schrieffer-Heeger 模型的拓扑性质*

李家锐 王梓安 徐彤彤 张莲莲 公卫江

(东北大学理学院,沈阳 110819)

理论上分析了受自旋指标调控并施以增益和损耗复势能的一维非厄米自旋轨道耦合Su-Schrieffer-Heeger(SSH)模型的拓扑性质和能谱特性.发现虚势能导致体系的拓扑非平庸区出现能谱虚化,而在拓扑平庸区发生 PT 相变.此外,虚势能和自旋轨道耦合共同作用使得拓扑平庸区中发生拓扑相变,并且拓扑非平庸区变宽.能谱结果显示,虚势能和自旋轨道耦合对于体系的零能态有明显的调控作用,主要在于出现了4 种局域性、数目均不同的零能态.这说明虚势能和自旋轨道耦合对体系的能带结构的特殊调节效果.本文有助于理解 PT 对称非厄米系统的拓扑相变行为.

1 引言

多年来,具有空间和时间反演组合对称性(PT对称性)的非厄米哈密顿量一直是量子物理领域的研究热点.PT对称性的概念最早是在1998 年由Bender 和Boettcher 提出的,他们发现在PT对称破缺发生之前,系统能够出现纯实数的本征能谱[1].随着非厄米和拓扑量子物理的发展,PT对称拓扑量子物理已经成为一个重要的研究方向[2-5].

在众多非厄米PT对称体系的结构中,Su-Schrieffer-Heeger (SSH)模型是最基本、最重要的体系之一[6-8].所谓的一维SSH 模型是一种具有交替跳跃系数的一维两能带晶格[9-12].在厄米情况下,通过调节胞内和胞间跃迁系数的比值,在布里渊区的边界处会出现能隙闭合再打开的过程,即拓扑相变[13].在开边界条件下,拓扑非平庸区的能隙中会出现局域在系统两端的零能边缘态.正因为SSH 模型清晰的拓扑特性,被视为非厄米拓扑量子物理的重要研究对象.朱保刚等[14]研究了在模型两端具有增益和损耗虚势能的PT对称非厄米SSH 模型.发现虚势能的加入会导致体系的拓扑平庸区和非平庸区表现出不同的特性.在拓扑平庸区中,虚势能会导致系统经历自发的PT对称破缺转变.而在拓扑非平庸区,仅会出现自发的PT对称破缺相.随后,许多课题组致力于研究PT对称非厄米SSH 模型的性质,讨论了自发PT对称破缺,添加次近邻耦合、拓扑相位以及奇异点和拓扑边态[15-21].在此基础之上,其他复杂结构也得到讨论,如PT对称的三聚体晶格、Kitaev 模型、六角蜂窝晶格等[22-25].

虽然在自然界中找不到特殊的PT对称系统,但实验上可以等效实现.如利用光波导通道可以得到具有增益和损耗效果的复势能[26],利用光学微腔或单向隐形Bragg 光栅结构实现PT对称[27,28].PT对称光学和拓扑光子学的发展直接推动了PT对称拓扑系统的发展.除了光学系统之外,在声学领域[29]以及LRC 电路中也能实现PT对称[30,31].

随着自旋轨道耦合体系研究的深入,有研究组指出自旋轨道耦合对厄米体系的拓扑性质具有重要影响和驱动作用[32-34].受此启发,本文拟设计一个复杂的体系,即在一维自旋轨道耦合SSH 模型的基础上施加与自旋方向相关的虚势能.目的在于,研究虚势能和自旋轨道耦合对一维自旋轨道耦合SSH 模型拓扑性质的共同驱动作用.研究发现,随着虚势能的增加,体系发生自发PT对称破缺.此外,虚势能和自旋轨道耦合共同作用会诱导拓扑平庸区发生相变,使得拓扑非平庸相的范围增加.在此过程中,两种参数对拓扑非平庸区也产生了不同特性的零能态.所有现象都表明了虚势能和自旋轨道耦合对非厄米自旋轨道耦合SSH 模型拓扑性质、边缘态特征等因素具有丰富的调控作用.

2 理论模型

本文提出的非厄米一维自旋轨道耦合SSH 模型是由Nc个原胞组成的一维链,具体结构如图1所示.体系哈密顿量表示为

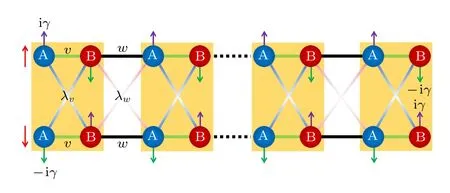
图1 非厄米自旋轨道SSH 模型示意图.A 和B 表示两种晶格,紫色上箭头和绿色下箭头分别表示具有增益和损耗的虚势能 iγ 和 - iγ,浅绿色线和黑色线分别表示胞内跃迁v 和胞间跃迁w,蓝色线和粉色线表示胞内自旋轨道耦合跃迁 λ υ 和胞间自旋轨道耦合跃迁λwFig.1.Schematic diagram of the non-Hermitian spin-orbit SSH model.A and B represent two kinds of lattices,and purple-up and green-down arrows represent imaginary potentials iγ and - iγ,respectively.Light-green and black lines denote intracell hopping v and intercell hopping w,and the blue and pink lines describe the intracell spin-orbit coupling λ υ and the intercell spin-orbit coupling λ w .

右侧第一项H0表示一维自旋轨道耦合SSH 模型的哈密顿量:

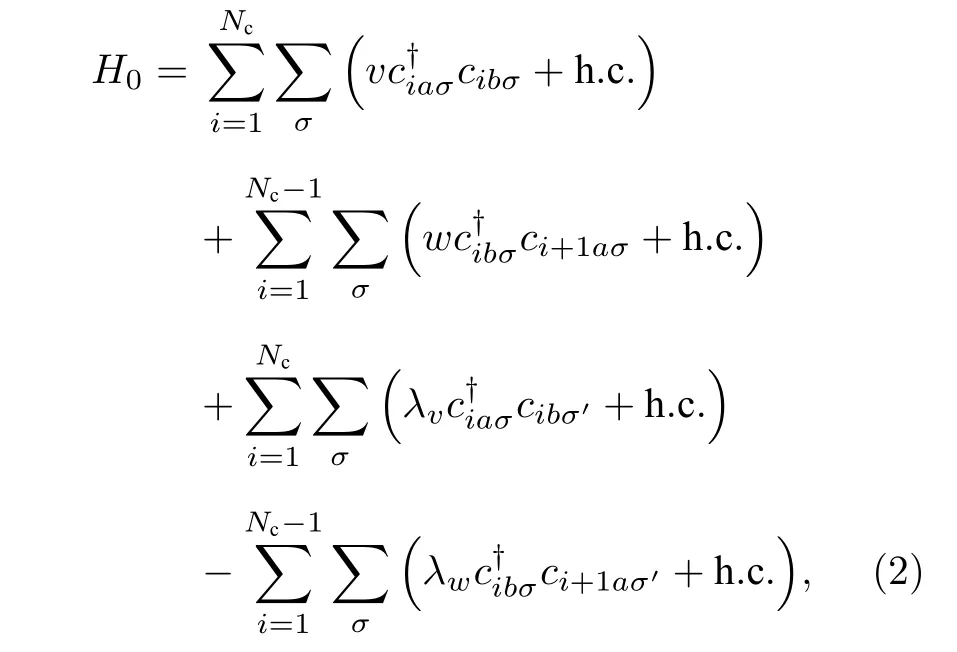
(2)式右侧第二项U描述在位能处引入能量增益和损耗来实现的虚势能项,其哈密顿量写为

2.1 对称性

哈密顿量的对称性决定了具有拓扑结构的系统中对称保护的拓扑相位.因此,应首先关注体系的对称性,以呈现自旋轨道耦合SSH 模型的拓扑性质.利用泡利矩阵,(5)式可以改写成:

根据所满足的对称性,可以将拓扑体系分类[35,36].可以推断厄米情况下本体系属于BDI 类,而在非厄米情况下属于非厄米系统38 种拓扑分类中的BDI†类,具体分类结果如表1 所列.以往的结论[35]表明,一维BDI 类体系存在类拓扑不变量.

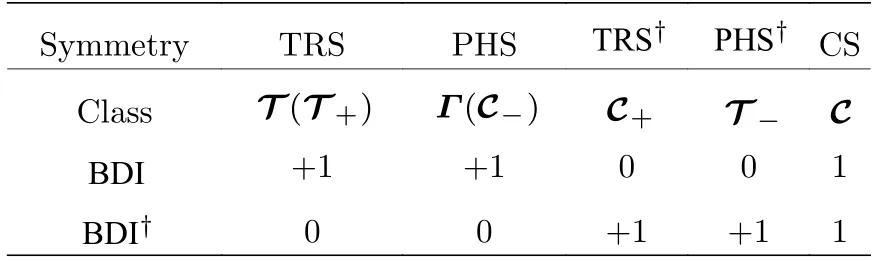
表1 厄米和非厄米情况的 B DI 和 B DI† 类Table 1. The B DI and B DI† classes for Hermitian and non-Hermitian Hamiltonians.

2.2 能带结构与拓扑相变

需要强调的是,只从对称性的角度确定体系的拓扑性质是不够准确的.下面计算一维非厄米自旋轨道耦合SSH 模型的能带结构,探究体系的拓扑相变条件.将(5)式的哈密顿量进行对角化处理,可以得到动量空间能带表达式:

通过能带表达式(9)能够发现,当k=±π 时中间两条能带发生闭合,此时λ,δ和t之间满足条件δ=±λ/t.同样,当三者满足δ=±t/λ时,中心能带在k=0处发生能隙闭合.如图2(a)和图2(b)所示的λ=0.3 时的能谱.可以发现,当δ=0.3 时中间两条能带在k=±π 相 交,而 当δ=3.333 时能隙 在k=0处闭合,与理论推导结果一致.

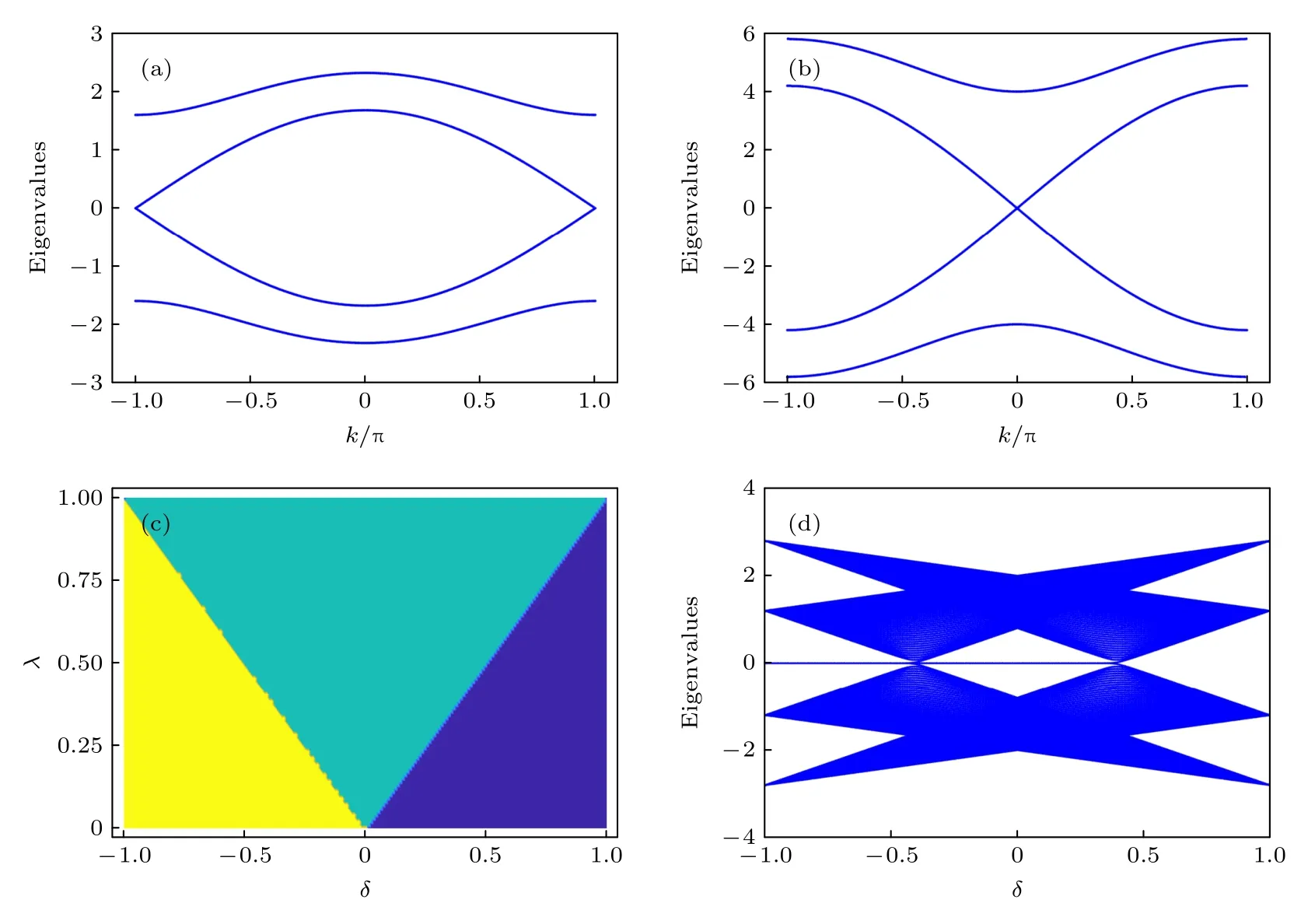
图2 (a),(b) 厄米情况下,体系的 动量空 间能谱 图,λ =0.3 (a) δ =0.4 ;(b) δ =2.5 .(c) 动量空 间相图,其中黄 色对应Z=2π,绿色对应 Z =π 以及紫色对应 Z =0 .(d) 体系能谱随着二聚化参量 δ 的变化Fig.2.(a),(b) The energy spectra of system in the momentum space under the Hermitian condition with λ =0.3 : (a) δ =0.4 ;(b) δ =2.5 .(c) Phase diagram in the momentum space,where yellow region corresponds to Z =2π,green region corresponds to Z=π,and purple corresponds to Z =0 .(d) Energy spectrum with the change of dimerization parameter δ .

根据 B DI 类对称性的结论,体系存在Z类拓扑不变量.将动量空间哈密顿量转换为非对角形式,代入拓扑不变量表达式

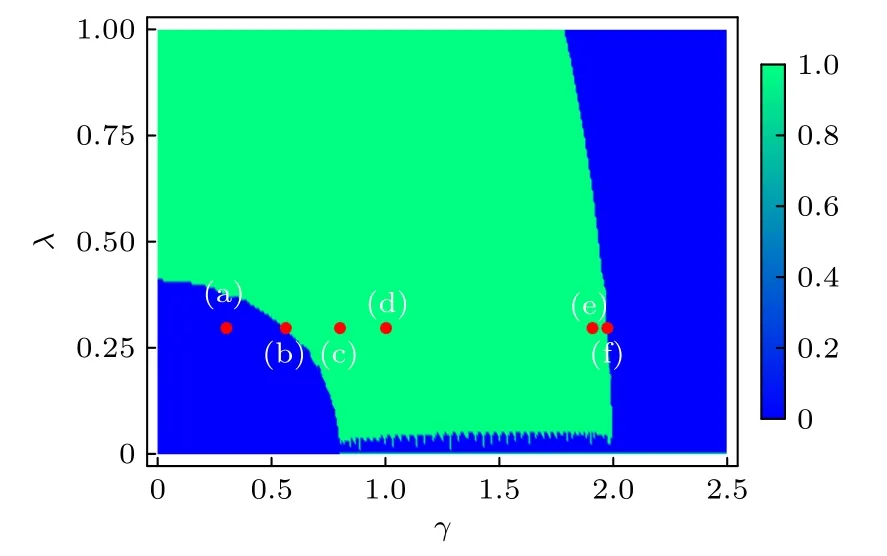
图3 随 γ 和 λ 变化的拓扑相图.蓝色对应 Z =π 的拓扑非平庸相,绿色区域表示=0 的拓扑平庸相.相关参数为 δ =0.4 以 及t=1.0Fig.3.Topological phase diagram with changes in γ and λ .Blue region corresponds to the topologically non-trivial phase of =π,and green region represents the topologically trivial phase of Z =0 .Relevant parameters are taken to be δ =0.4 and t =1.0 .

3 数值结果与讨论

基于上述理论推导,接下来从动量空间和坐标空间出发,详细讨论非厄米一维自旋轨道SSH 模型的能带结构.为方便计算,整篇文章中取t=1.0 .

图4 给出了在动量空间中非厄米一维自旋轨道耦合SSH 模型的能谱.参数设置为λ=0.3 和δ=0.4,对应厄米情况下的拓扑平庸区.从图4 可以发现,随着γ的增加,体系确实经历了两次相变过程,这意味着虚势能在调控体系的拓扑属性方面扮演了重要角色.具体来说,从图4(a)和图4(b)可以观察到,当γ增加至时,中间两条能带在k=±π处相遇.在这个过程中发生了拓扑相变,与(11)式结果一致.随着γ继续增加,闭合的能隙重新打开.在γ=0.8 时(如图4(c)),上下两条能带在k=±π 处相交,此时简并点能量为|E|=2λ.当γ＞2δt时,虚势能使简并点劈裂成两个与PT对称性破缺相关的奇异点,此时出现能量虚部.当γ ≈1.986 时,能隙重新在k=0 处闭合,且闭合点的能级虚部 I m(E)=0 (如图4(e)).这说明了体系发生第二次相变,而且条件与(12)式一致.随着非厄米势能的增加,两个奇异点继续移动,复能区逐渐扩展到中心.在γ=2t=2.0 时,两个奇异点在k=0处合并,虚部在k=0 处形成狄拉克锥,此时实部能量为E=±2δλ(如图4(f)).最后,γ＞2t时,整个体系的能量全部为复数,不再存在奇异点.根据以上结果,可以确定虚势能在非厄米自旋轨道耦合SSH 模型中诱导出了丰富的能带结构.

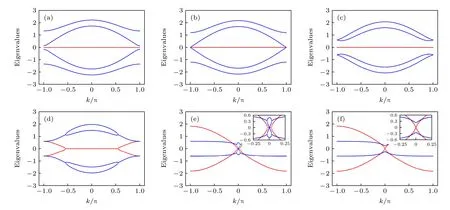
图4 不 同虚势能 γ 的能带结构 (a) γ =0.3 ;(b) γ =/5 ;(c) γ =0.8 ;(d) γ =1.0 ;(e) γ ≈1.986 ;(f) γ = 2 .0 .对 应于图3中标出的各个位置.蓝线表示能量的实部,红线对应于虚部.其他参数为λ=0.3和δ=0.4Fig.4.Band structures for different values of imaginary potentialγ: (a)γ=0.3;(b)γ=/5 ;(c) γ = 0 .8 ;(d) γ =1.0 ;(e) γ ≈1.986 ;(f) γ =2 .Correspond to the respective points in Fig.3.The blue lines indicate the real part of energy,and the red lines correspond to the imaginary part.Other parameters are λ =0.3 and δ =0.4 .

接下来讨论开边界情况下体系的能谱结构,相关参数取λ=0.3 .根据厄米情况的结论知道,当δ ∈[-1.0,-0.3] 时,存在四重简并零能,而在δ ∈[-0.3,0.3]时表现为二重简并零能,剩下区域δ ∈[0.3,1]为拓扑平庸区.

图5 给出的是在Nc=50 的条件下能带的实部和虚部.由(11)式和(12)式可知,非厄米情况下体系在和δ3(4)=处会发生相变.从能量的实部和虚部图中可以发现,虚势能对于体系的拓扑非平庸和平庸相的体态和零能态具有不同的调控作用.首先,对于拓扑平庸区而言(厄米 0.3＜δ＜1),随着γ的增加,由虚势能诱导的零能态区域逐渐变宽.当γ=1.908 时,达到拓 扑相变条件δ1,在δ ∈[0.3,1.0]全区间内存在零能态(如图5(e)).在整个过程中新产生的零能态无虚部出现.而在拓扑非平庸区(厄米δ∈[-1.0,0.3])中,虚势能对两个非平庸相的作用效果不同.虚势能的加入导致厄米的四重简并零能态出现虚部,即E=0±ib,说明该阶段发生PT对称破缺,而原来二重简并的状态仍表现为纯实数的零能.γ的增加使满足δ2的拓扑相变点逐渐靠近δ=-1.0,导致原来四重零能态区域减小,二重零能态区域逐渐增大.另外,在δ ∈[-δ2,0] 中出现从体态析出的孤立态.随着δ趋近于-1.0,孤立态也逐渐进入到零能态中并伴有能量虚部,形成具有纯实零能又有纯虚能的混合六能态区域.由于该部分的零能态不是由于能隙闭合再打开产生,推断其不具有拓扑性.当γ=2.0 时,拓扑相变的破缺导致体系不再存在拓扑相,仅存在具有虚势能的能态.对于体态,在-γ/2＜δ ＜γ/2范围内体态有虚部出现,发生PT对称破缺,而其余区域的体态均为实数.以图5(d)为例,当γ=2.0时,整个参数空间的体态都有虚部.基于以上结果,可以发现虚势能对于开边界条件下的的能带结构和拓扑态具有明显的调控作用.

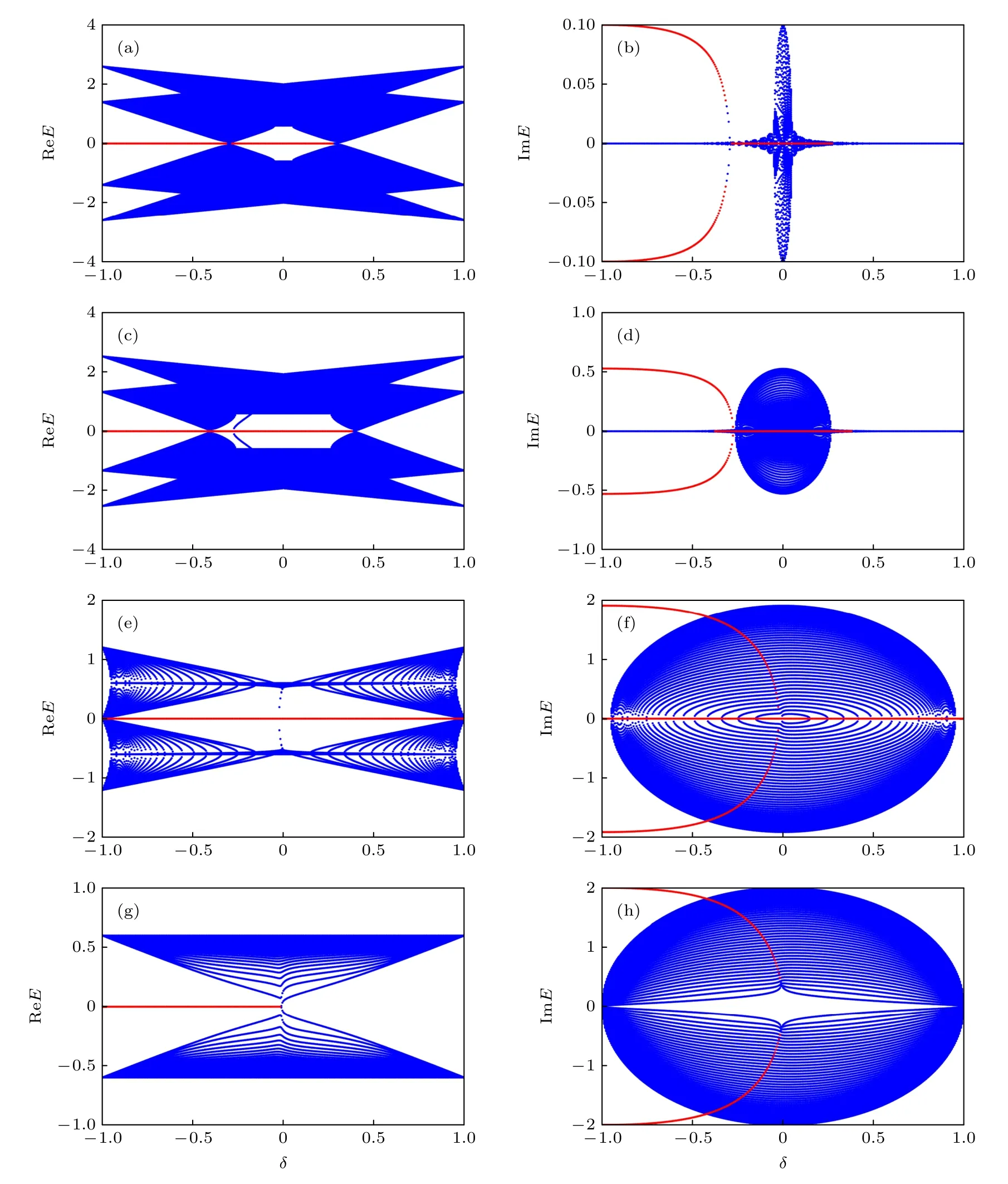
图5 开边界情况下,不同 δ 的能量实部和虚部 (a),(b) γ =0.1 ;(c),(d) γ =/5 ;(e),(f) γ ≈1.908 ;(g),(h) γ =2.0 .左侧显示能量的实部,右侧对应于能量的虚部.其他参数设为 λ =0.3 .图中红线代表零能态的实部和虚部Fig.5.Real and imaginary parts of energy for different δ : (a),(b) γ =0.1 ;(c),(d) γ =/5 ;(e),(f) γ ≈ 1 .908 ;(g),(h)γ=2.0.Left panel shows the real part of energy,and the right corresponds to the imaginary part of energy.Other parameters are λ=0.3.The red lines denote the real and imaginary parts of zero energy states.

为了更好地描述体系中零模的特征,图6(a)—(d)依次给出了δ=-0.7,δ=-0.32,δ=-0.23 及δ=0.32时的本征能谱和波函数概率密度.可以观察到,不同区域的零能态呈现出异样的特征.具体在于,当δ=-0.7 时,在能隙中存在四个纯虚能态.图6(a)概率密度谱中(i) 和(iii)对应 0 +0.514i,(ii)和(iv)对应 0-0.514i .由于虚势能的加入导致本征能量变为复数,四个态都呈现局域在晶格的左端或右端的趋势,并且相同能量的两个态的局域性相反.图6(b)对应δ=-0.32 的结果.可以看出,能隙中存在六个态,其中四个有虚能量,两个能量为纯实数.从前面的结果可知,有能量虚部的态是由体态中析出的孤立态导致的,不具有拓扑性.从概率密度可以发现,两个纯实零能态(i)局域在系统的两端.四个能量为 0 +0.271i (ii)和 0-0.271i (iii)的态也呈现局域在系统两端的趋势.为了确定从体系析出的孤立态情况,图6(c)给出了δ=-0.23 的结果.从能谱可以观察到,新产生的孤立态是二重简并的,在能隙中间形成纯实能的二重简并零能态.从概率密度可知,孤立态和零能态一样,都呈现局域在系统两端的趋势.然而,与孤立态产生的零能模相比(图6(b)中(ii)和(iii)),局域性相对较弱.最后,当γ=0.32 时,虚势能的加入导致原有的拓扑平庸区的间隙中出现局域在系统两端的二重简并零能态,如图6(d)所示.综上所述,虚势能的加入导致原来的拓扑平庸区的间隙中出现局域在系统两端的二重简并零能态,而随着体态析出的二重简并孤立态进入到零能态中,导致原有二重实零能态变为六个态.这说明虚势能可以让体系的零能态呈现出更加有趣的现象.

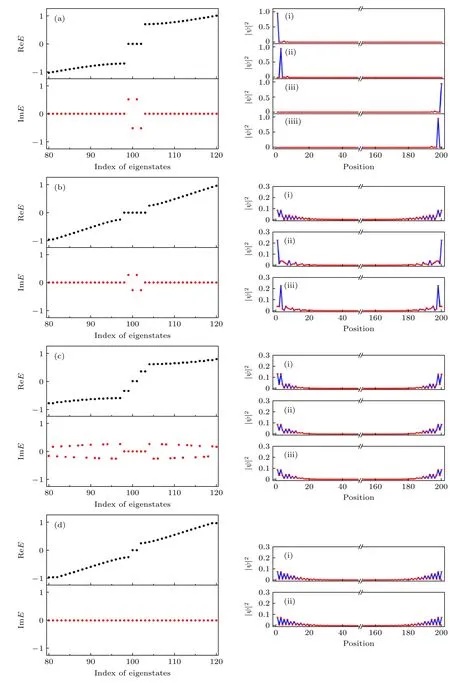
图6 开边界条件下的能谱和概率密度谱 (a) δ =-0.7 ;(b) δ =-0.32 ;(c) δ =-0.23 ;(d) δ =0.32 .其他参数设为λ=0.3以及γ=/5Fig.6.Energy and probability density spectra with open boundary conditions: (a) δ =-0.7 ;(b) δ =-0.32 ;(c) δ =-0.23 ;(d)δ=0.32.The other parameters are λ=0.3 andγ=/5 .

下面讨论虚势能强度γ对不同区域能谱结构的影响,如图7 所示.其中图7(a)和图7(b)对应δ=-0.4,图7(c)和图7(d)对应δ=-0.2 以及图7(e)和图7(f)对应δ=0.4 .它们分别描述厄米体系中四重简并、二重简并的拓扑非平庸区和拓扑平庸区.从图7(a)和图7(b)可以发现,在γ＜2δt=0.8 区间内体态能量为实数,而γ＞0.8 区间内体态能量有虚部出现.对于零能态,只要γ不等于零,它的本征能量立刻呈现出虚部,导致体系一直PT破缺.此外,在两次拓扑相变点＜1.986之间,虚势能驱动了新的纯实零能态出现;当γ＞1.986,有虚势能驱动的拓扑相变破缺,纯实零能态消失.在δ=-0.2 的情况 下(图7(c)和 图7(d)),当γ ＜0.4 时,整个体系处于严格的PT对称;当γ ＞0.4时,由于体态能量存在虚部,因此发生PT对称破缺.除此之外,随着γ的增加,可以看到确实从体态中析出二重简并孤立态.由于孤立态产生的零能加入,导致在γ＞1.4 后出现混合六能态区.直到第二次拓扑相变之后,体系的零能转变为四重纯虚能态.最后,对δ=0.4 的情况,如图7(e),(f)所示,体系经历PT相 变,即 在γ＞0.8 处发生PT对称破缺.此外还能发现,在两次拓扑相变之间的间隙中出现有二重拓扑零能态.基于以上结果可以看出,对于厄米情况下不同类型的拓扑相,虚势能会对零能和体态产生不同的作用效果.

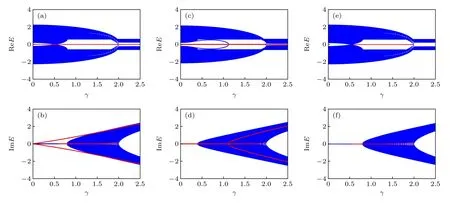
图7 γ 变化对能量实部和虚部的影响 (a),(b) δ =-0.4 ;(c),(d) δ =-0.2 ;(e),(f) δ =0.4 .左侧显示能量的实部,右侧对应于能量的虚部.其他参数为 λ =0.3 .图中红线代表零能态的实部和虚部Fig.7.Real and imaginary parts of energy for different γ : (a),(b) δ =-0.4 ;(c),(d) δ =-0.2 ;(e),(f) δ = 0 .4 .Left panel shows the real part of energy,and the right corresponds to the imaginary part.Other parameters are λ =0.3 .The red lines describe the real and imaginary parts of zero energy states,respectively.

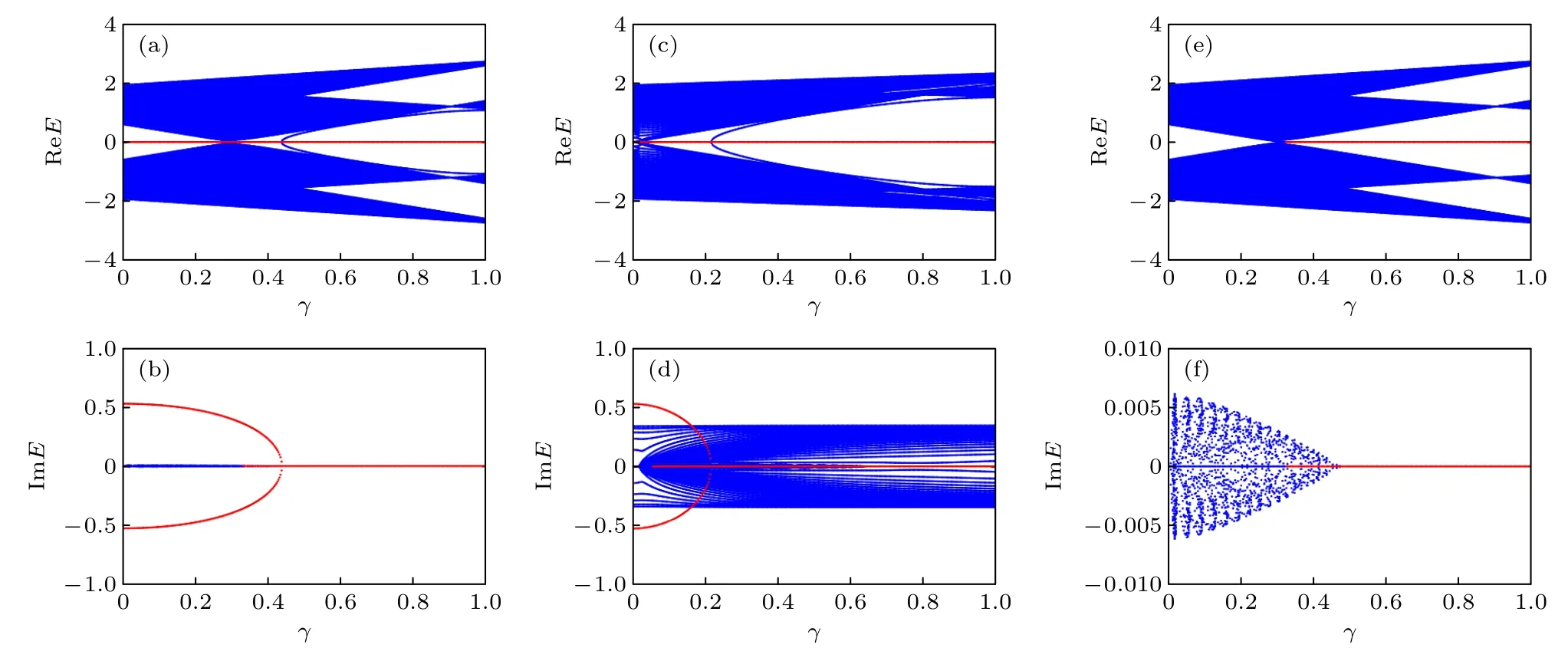
图8 不同λ导致的能量实部和虚部(a),(b)δ=-0.4;(c),(d) δ=-0.2 ;(e),(f) δ =0.4 .左侧显示能量的实部,右侧对应于能量的虚部.参数设置为γ=/5.图中红线代表零能态的实部和虚部Fig.8.Real and imaginary parts of energy for different λ : (a),(b) δ =-0.4 ;(c),(d) δ =-0.2 ;(e),(f) δ = 0 .4 .Left panel shows the real part of energy,and the right corresponds to the imaginary part.Other parameters are γ =/5 .The red lines describe the real and imaginary parts of zero energy states,respectively.

4 结论

本文在一维自旋轨道耦合SSH 模型中,通过施加具有增益和损耗的虚势能来构造一维PT对称体系,着重考察了由虚势能和自旋轨道耦合驱动的拓扑相变以及零能态的特性.结果发现,自旋轨道耦合和虚势能的作用导致体系出现了丰富而有趣的现象.首先,虚势能的加入让拓扑非平庸体系发生自发PT对称破缺,而在拓扑平庸区中可以观察到PT对称相变,即从严格PT对称到PT对称破缺.其次,虚势能和自旋轨道耦合的共同作用导致非平庸区中出现不同特性、不同数量的零能态:I) 四个能量为 0±ib型的能态;II) 由于从体态析出的二重孤立态进入零能态中而产生的具有二重纯实零能态和四个纯虚能态的混合六能态区域;III) 具有纯实零能的二重简并零能态.对于拓扑平庸区而言,虚势能和自旋轨道耦合共同作用使厄米情况下的拓扑平庸区发生拓扑相变,在平庸区的间隙中出现二重纯实数零能态,拓宽了体系的拓扑非平庸区.相信以上结果有助于探究PT对称非厄米系统的拓扑相变行为,同时为探究非厄米零能态的种类和性质提供了理论支持.