复杂系统中的层次结构提取与分析*

范开宇 刘艳华 杨培才 吴吉哲 王革丽†

1) (大连市气象局,大连 116001)

2) (中国科学院大气物理研究所,中层大气和全球环境探测重点实验室,北京 100029)

3) (黑龙江省气象服务中心,哈尔滨 150036)

4) (蒙阴县气象局,蒙阴 276200)

气候系统是一个非平稳复杂系统的事实已经得到了广泛认同,产生这种非平稳性质的根本原因在于气候系统存在的层次结构,处于高层系统中的外强迫信号随时间发生变化,造成了大气运动的非平稳现象.慢特征分析法可以从快变的非平稳信号中提取慢变的外强迫信号,并已应用于气候系统的归因分析中.本文利用慢特征分析法提取改进的Henon 映射模型构造的非平稳时间序列以及北京月平均气温的外强迫信号,并且使用小波变换方法对外强迫信号的尺度特征及物理背景机理进行分析.结果表明,气候系统受到长周期的外强迫信号与短周期外强迫信号的共同作用.同时,长周期的外强迫信号影响短周期外强迫信号.该工作有助于理解气候系统的层次结构特征.

1 引言

近些年,随着气候系统平稳性的改变不断被证实,气候系统是一个非平稳复杂系统的事实已经得到了广泛的认同[1-5].外强迫因子随时间发生变化是导致气候系统非平稳性质产生的根本原因.外强迫因子如何影响气候系统一直受到科学家的关注.复杂系统的内部一般都包含着层次结构,而这种非平稳现象的发生正是由于层次结构的存在[6-10].对气候系统来说,处于高层系统的外强迫随时间发生变化,在大气运动中引发了非平稳现象.所以,如何从气候信息中提取出外强迫驱动因子,并对提出的外强迫因子进行分析,对提高人们对气候过程本质的认识以及发展新的建模理论具有至关重要的意义.

慢特征分析法(slow feature analysis,SFA)是一种非监督的学习方法,它起源于生物视觉领域,它能够从给定的快变非平稳序列中提取出缓慢变化的外强迫信号.Konen 和Koch[11]通过一系列实验发现,SFA 方法提取出的信号分量只是一个单一的变化最慢的外强迫信号,它可能包含了所有外强迫信号分量.潘昕浓等[12]通过构建层次结构系统模型来测试SFA 方法提取外强迫信号的能力,取得了成功.对于SFA 方法的探索与应用为理想非平稳模型外强迫信号提取提供了新的方法手段,也为气候系统驱动力物理机理的研究提供了新的方向.杨培才等[13]使用SFA 方法对北半球的月平均气温时间序列外强迫进行了重建,利用小波变换技术分析了外强迫的尺度特征,并探究了背后的物理机理,推断太阳22 a 磁周期(the Hale cycle)和大西洋多年代际振荡(atlantic multidecadal oscillation,AMO)的影响.王革丽等[14]利用SFA 方法对Arosa 臭氧观测资料的外强迫进行了提取,重建的外强迫信号的小波分析表明,存在着两个明显的周期,可能对应着太阳活动和北大西洋涛动(north atlantic oscillation,NAO),体现了太阳与海洋活动对臭氧浓度变化的显著影响.

本文将在Henon 映射模型中加入具有层次结构的外强迫信号,构造非平稳复杂系统来测试SFA 方法的提取能力.并以北京月平均气温时间序列为例,利用SFA 方法,对其进行外强迫的提取,结合小波变换对北京月平均气温时间序列外强迫的尺度结构与可能存在的物理机理进行分析,探寻其中的层次结构.

2 SFA 简介

SFA 是由Wiskott 和Sejnowski[15]提出的一种信号处理方法,它可以在一个已知的复杂多维时间序列中得到一个缓慢变化的信号分量.SFA 方法可以保证从一般的有限维度函数空间中获取全局最优解,并且在模拟的过程中,能够依据原始信号的大小与尺寸对输出结果进行合理有效的调整[16].SFA 方法是在Packard 状态空间重构理论[17]与Takens 嵌入定理[18]的思想上建立的,经过函数空间重构,再经过标准化、非线性扩展、球化以及主分量分析等一系列处理,将原始信号向变化最慢的方向投射,得到的这个分量即可视为原始信号的外强迫信号.下面对慢特征分析法的主要算法步骤进行简要介绍.

重构后的序列长度N=n-m+1 .

然后,利用(1)式中产生的一阶项和二阶项进行非线性扩展,得到一个k维的函数空间H(t) :

方便起见,记为

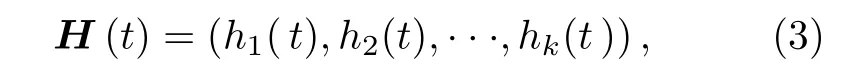
进行积分,求得输出信号:

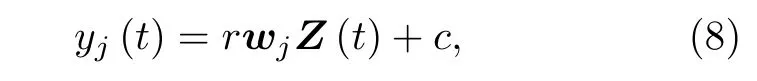
(8)式中r与c均为常数.选取最小的特征值λ,将对应的权重向量w代入到(8)式中,即可得到原始信号最慢变的分量信号,即外强迫信号.由于在积分的过程中产生了常数r与c,所以通过SFA 方法获取的外强迫信号与真实的外强迫相比,相差一个放大因子和平移因子.

3 模型实验

Henon 映射是一种可以产生混沌的动态系统,它仅包含一个非线性项,因此它是高维非线性映射中最简单的映射[19].它的动力学方程为

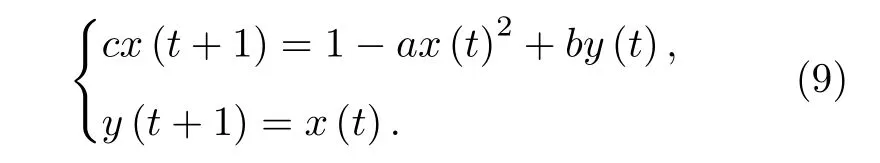
Henon 映射的收敛性只与参数a和b有关,与初值无关.最经典的Henon 映射是令参数a=1.4,b=0.3,此时系统可进入混沌状态.

Lyapunov 指数是用来判断非线性系统存在混沌运动的特征数值之一,可以衡量系统动态特性.当系统存在一个Lyapunov 指数为正数时,系统一定处于混沌状态,在实际应用中,通常把最大Lyapunov 指数的正负作为判断指标[20,21].本文将最大Lyapunov 指数作为判断系统模型是否处于混沌状态的判据.

利用正弦函数,将小周期的正弦信号作为基频信号,将大周期的正弦信号作为调制信号,构造一个具有层次结构的时变参数,设置基频信号

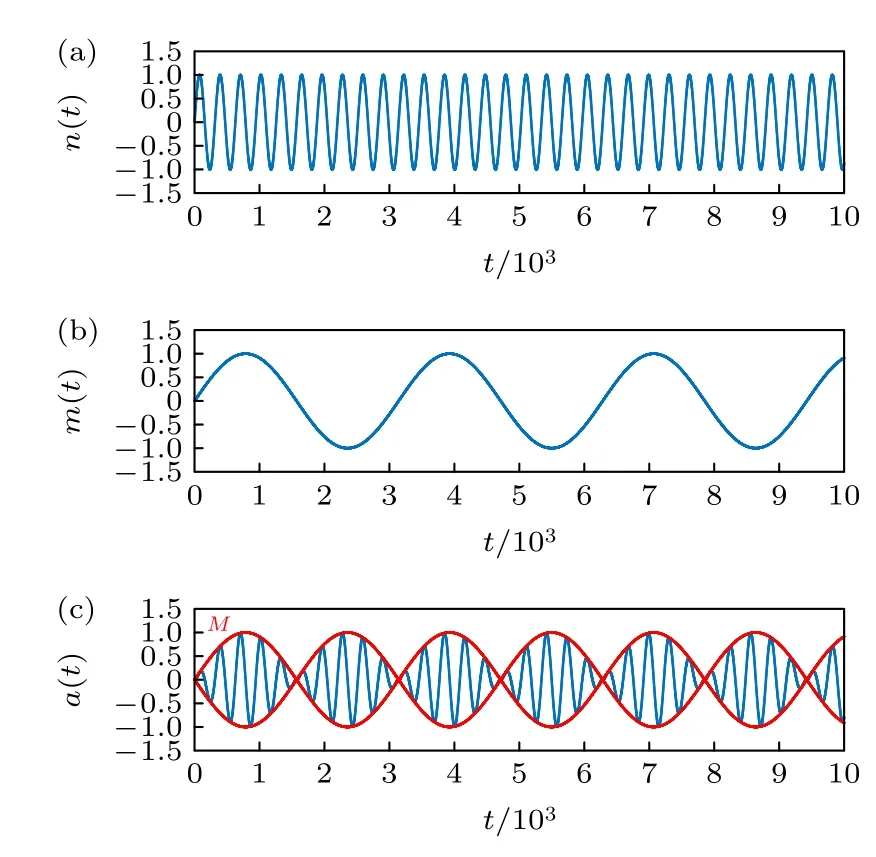
图1 (a) 基频信号 { n(t)} ;(b) 调制信号 { m(t)} ;(c) 时变参数 { a(t)} (蓝线)与其调制信号(包络)M(红线)Fig.1.(a) Fundamental frequency signal { n(t)} ;(b) modulation signal { m(t)} ;(c) time-varying parameter{a(t)}(blue line) and its modulation signal (envelope) M (red line).

将{a(t)}作为外强迫信号,并代入Henon 映射模型{y(t)}中[22]:

将时变参数{a(t)}迭代10000 次得到序列记 为{s1(t)}t=1,2,···,10000,然后将{s1(t)}作为外强迫信号代入(13) 式中,迭代10000 次得到{y(t)}t=1,2,···,10000.选 取{y(t)}的第一 维序列{y1(t)}进行系统动态特征的判断,经计算{y1(t)}前600 步的最大Lyapunov 指数λ=0.3938,说明{y1(t)}处于混沌状态.截取{y1(t)}后5000 个数据作为非平稳时间序列模型进行外强迫信号提取(图2(b)),嵌入维数m=13,时滞系数τ=1,得到外强迫信号{as1(t)}如图2(c)所示.可以看到,外强迫信号{as1(t)}是一个明显的调幅信号,其信号包络即为调制信号M.将提取出的外强迫信号{as1(t)}与真实外强迫信号{s1(t)}进行比较,发现提取的{as1(t)}缺少一个放大因子,对其进行标准化处理后再与真实外强迫信号进行比较,二者变化趋势具有较好的一致性,相关系数可以达到0.98(图2(d)).

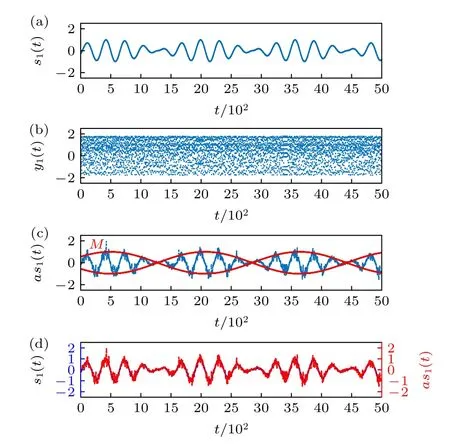
图2 (a) 真实外强迫信号 { s1(t)} ;(b) 非平稳时间试验序 列 { y1(t)} ;(c) SFA 方法提 取得到 的外强 迫{as1(t)}(蓝线)及其包络 M(红线);(d) 外强迫 { as1(t)} (红线)及真实外强迫信号 { s1(t)} (蓝线)比较Fig.2.(a) The true driving force signal { s1(t)} ;(b) the testing non-stationary time series { y1(t)} ;(c) the driving force signal extracted by SFA method { as1(t)} (blue line)and its modulation signal (envelope) M (red line);(d) the driving force signal extracted by SFA method{as1(t)}(red line) and the true driving force signal { s1(t)} (blue line).

从外强迫信号的提取实验中可以看到,利用快变信号作为基频信号,慢变信号作为调制信号生成具有层次结构的外强迫信号,将其加入到Henon映射模型中构造非平稳的混沌系统.利用SFA 方法可以成功将外强迫信号提取出来,提取出的外强迫信号层次结构清晰完整,基频信号和调频信号与系统的外强迫初始信号一致.

4 气温时间序列的外强迫重建与分析

在前期的工作中,我们重建了北京月平均气温距平时间序列的外强迫信号,测试了SFA 方法对嵌入维数选取的敏感性,结果表明,在一定范围内选取不同的嵌入维数,提取得到的外强迫信号差别不大.并结合小波分析对外强迫信号所包含的周期、尺度特征进行了讨论[23].从外强迫信号的6 个特征尺度中,找到了与太阳22 a 磁周期(the Hale cycle)、太阳11 a 黑子周期(the Schwabe cycle)以及东太平洋赤道海区海表温度周期对应的尺度分量,并发现这些特征尺度间存在着谐波关系(如表1 所列).本文将在前期工作的基础上,进一步对这些外强迫信号的尺度特征及可能的物理机理进行深入分析,分析过程如图3.

图3 北京月平均气温外强迫信号的提取与分析流程图Fig.3.Flow chart of extraction and analysis of driving force signal of monthly mean temperature of Beijing.

表1 北京月平均气温时间序列外强迫信号小波分析周期频率及谐波关系Table 1. Periods and frequencies of the driving force signal of temperature extracted by SFA method of Beijing.

利用带通滤波器,将各个尺度对应的信号分量提取出来,如图4(a)—图4(f)中黑色曲线所示,这些信号分量揭示了外强迫信号各个尺度在时域上的基本特征.从图4 可以看到,除了S5和S6尺度分量外,其他尺度分量的振幅都受到调制信号的调制.因此,考虑利用正弦函数来绘制信号包络,恢复这些调制信号,结果如图4(a)—图4(f)中蓝色曲线.这些调制信号的周期远比尺度分量自身的周期大得多,它们的相位变化反映出对应尺度分量的能量变化.其中,尺度分量S2的调制信号可用正弦函数近似表示为

类似于S2,尺度分量S3和S4的调制信号可以近似表示为

M3和M4这两个调制信号反映了尺度分量S3和S4振幅在时域上的变化特征.在1986 年S3和S4的振幅达到最小,在1986 年前振幅减小,此后振幅增大.它们与S2振幅变化呈相反趋势.通过观察,尺度分量S1同样受到一个周期性的调制信号调制,这个调制信号可以近似表示为

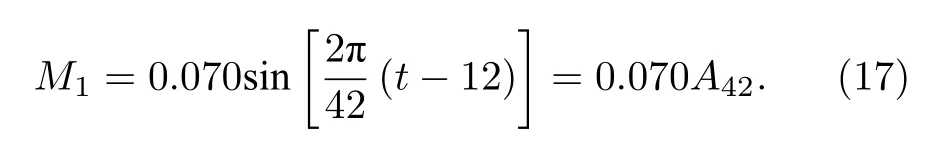
从图4(a)可以看出,尺度分量S1的振幅存在准42 年周期振荡,在1955,1976 和1997 这三个年份,振幅达到最大.在1965,1986 和2007 三个年份振幅达到最小.

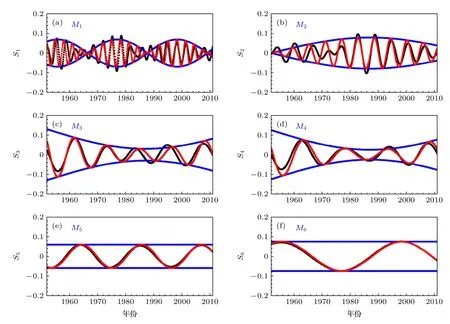
图4 (a)—(f)北京月平均气温外强迫信号特征尺度 S 1 — S 6 对应的信号分量Fig.4.(a)—(f) Signal components corresponding to the characteristic scale S 1 — S 6 of the driving force signal of monthly mean temperature in Beijing.

尺度分量S5和S6的振幅较为稳定,为固定常数,M5=0.06,M6=0.075 .

利用以上调制信号M1—M6,我们尝试对尺度分量S1—S6进行拟合,并记为(n=1,2,···,6),具体表述如下:

模拟的尺度分量信号—如图4(a)—(f)中的红色曲线.将模拟信号与实际尺度分量进行比较,相关系数记为R,标准差之比记为Ds′/Ds,具体结果见表2 所列.

表2 模拟尺度分量 — 与真实尺度分量信号 S 1 — S 6 比较Table 2. Comparison of analog scale component signal — and real scale component signal S 1 — S 6 .

表2 模拟尺度分量 — 与真实尺度分量信号 S 1 — S 6 比较Table 2. Comparison of analog scale component signal — and real scale component signal S 1 — S 6 .

值得注意的是,在实验的过程中发现尺度分量S1的调制信号M1周期为42 a 左右,这与尺度分量S6的周期十分接近.通过对比观察,发现M1与S6曲线变化趋势基本一致,如图5 所示.对二者进行比较表明它们的相关系数达到0.98.

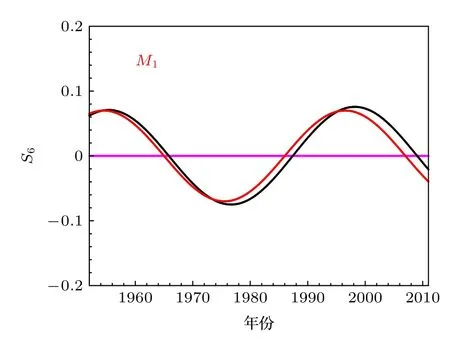
图5 尺度分量 S 6 (黑线)与调制信号 M 1 (红线)比较Fig.5.Comparison of scale component signal S 6 (black line) and modulated signal M 1 (red line).

将尺度分量S6作为尺度分量S1的调制信号,对S1进行拟合,结果如图6 所示.图6 中黑色曲线为尺度分量S1,蓝色曲线为调制信号,即尺度分量S6,红色曲线为利用分量S6拟合的分量信号,记为.表示为

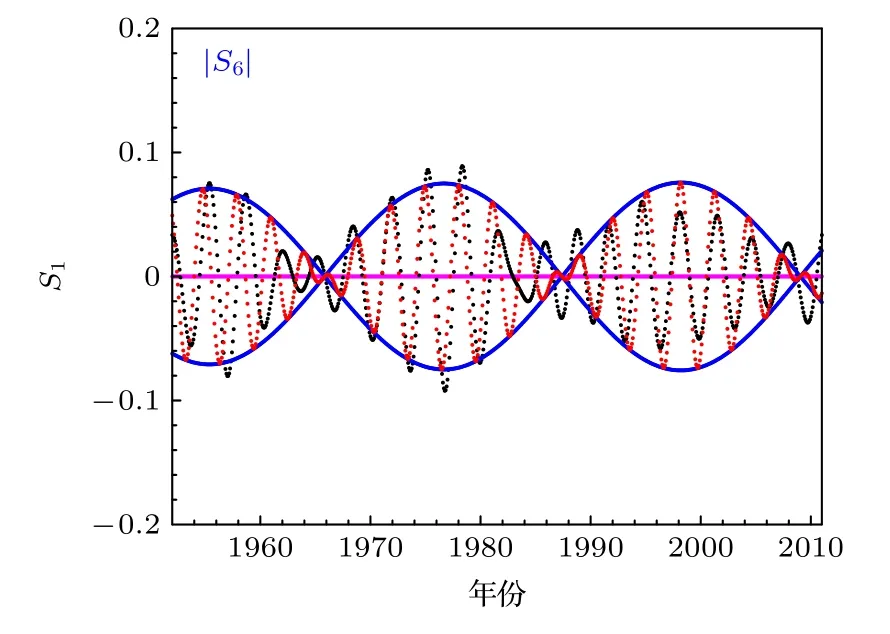
图6 利用尺 度分量 S 6 (蓝 线)来拟合 尺度分 量 S 1 (黑线)得到结果 (红线)Fig.6.Use the scale component signal S 6 (blue line) to simulate the scale component signal S 1 (black line) to obtain the result (red line).

S1分量的物理背景被认为是东太平洋赤道区海表温度的周期变化,S6分量的物理背景被认为是与太阳黑子周期有关,S6分量可以看作是S1分量的调制信号,且二者共用作用北京月平均气温温度时间序列,这样的结果体现了气候系统的层次结构,如图7 所示.长周期的外强迫信号与短周期外强迫信号共同作用于气候系统.同时,长周期的外强迫信号也影响短周期外强迫信号.

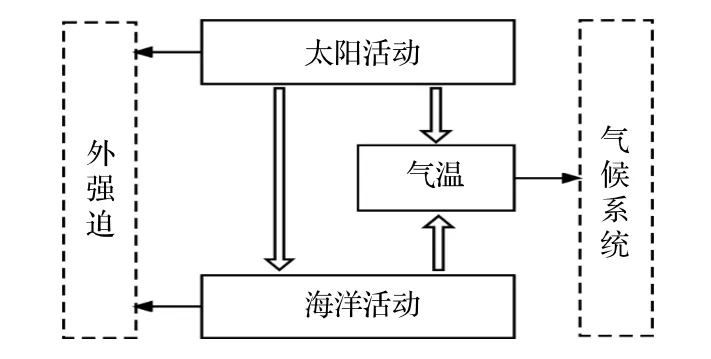
图7 气候系统的层次结构示意图Fig.7.Schematic diagram of the hierarchy of the climate system.

5 结论与展望

本文将具有层次结构的外强迫信号加入Henon 映射模型中,构造非平稳复杂系统来测试SFA 方法的提取能力.并将北京月平均气温作为真实气候要素时间序列进行外强迫的提取和分析,结合小波变换技术对外强迫的尺度结构与可能存在的物理机理进行分析,探寻其中的层次结构,主要结论如下.

1)在Henon 映射模型外强迫提取实验中加入包含快变和慢变这样具有层次结构的外强迫信号,SFA 方法可以从非平稳的Henon 映射模型中提取出快变信号,它的包络表现为慢变信号;提取出的外强迫信号与真实外强迫的相关系数达到0.98.

2)在对北京月平均气温时间序列的外强迫信号提取实验中,通过利用小波变换技术分析发现,北京月平均气温时间序列的外强迫信号存在6 个明显的特征周期,可推断其中的11.6 a,21.3 a 和42.7 a 周期代表了太阳活动,3.2 a 周期代表了海洋活动,它们共同作用于气候系统.

3)利用正弦函数对外强迫信号6 个尺度分量进行模拟表明,外强迫信号尺度分量的振幅受到调制信号的调制,调制信号的相位变化反映出对应尺度分量的能量变化.其中,42 a 周期的尺度分量与3.2 a 周期尺度分量的调制信号具有较高的相似程度.利用42 a 周期的尺度分量作为调制信号对3.2 a周期的尺度分量进行拟合,相关系数达0.588,可以揭示出气候系统的层次结构.长周期的外强迫信号与短周期外强迫信号共同作用于气候系统,同时,长周期的外强迫信号还在影响短周期外强迫信号.

本文的工作有助于理解气候系统的层次结构和驱动成因,以及驱动因子间复杂的相互作用.SFA 方法在实际应用中,嵌入维数和时滞参数的选取还没有一个普适方法.对于嵌入维数来说,可以通过敏感性实验来考察提取的效果.在一定范围内,嵌入维数的选取对结果影响不大,还会增加计算时间,损耗序列长度;对于时滞参数的选取,还需要更多的探索,目前只能依靠经验和大量试探进行选取.另外,在不同的时间尺度上,存在的耦合层次关系是否不同.特别是,如何结合气候系统内在物理机理的理解,进一步探究气候系统的层次结构特征以及影响因子之间的相互作用.这些问题需要在今后的研究工作中继续探索.