一类非线性互补问题的新修正谱梯度投影方法

林 婷，柯艺芬，张 振，马昌凤

(1.福建师范大学数学与统计学院，福建，福州 350117；2.中国科学院大学计算地球动力学重点实验室，北京 100049)

考虑如下形式的非线性互补问题(NCP)：求x∈Rn，满足

x≥0,f(x) ≥0,xTf(x)=0,

(1)

非线性互补问题在运筹学[1-2]、工程设计[3-4]和经济均衡[4-5]等方面有许多重要的应用，并发展了许多求解非线性互补问题的数值方法.

近年来，光滑函数法在求解NCP问题上引起了广泛的关注[6]，主要原因是其优越的数值性能．光滑函数法的思想是使用一个光滑函数将非线性互补问题(1)重新表述为光滑方程组，在迭代步中使用牛顿法近似求解光滑方程组.

在光滑函数中,Fischer-Burmeister (FB)函数受到广泛的关注.FB函数的定义如下

其中(a，b)∈R2.

然而，由于在牛顿法中求解雅可比矩阵及其逆矩阵需要大量的计算工作，因此求解光滑方程组代价是昂贵的．为了减少计算量，无导数法以及梯度法是目前比较有效的方法.

Jiang[7]利用平方FB函数转化的等价非线性方程组，在非线性映射方向可微且强单调情况下建立了一种无导数下降法；Mangasarian 等[8]通过最小化隐式拉格朗日函数，给出了强单调NCP的无导数下降方法，并建立了该方法的全局收敛性；Ma 等[9-10]提出了求解NCP的光滑Broyden-like 方法，该方法基于光滑逼近的FB 函数，并利用了无导数线搜索规则，证明了该算法在适当的条件下具有全局和超线性收敛性.

最近，Yu 等[11]提出了一类求解凸约束的非线性单调方程的改进谱梯度投影方法，其步长由长Barzilli-Borwein (BB)步长和短BB步长的凸组合决定，该算法具有良好的数值性能.

基于上述工作的启发，本文提出了一类求解非线性互补问题的新修正谱梯度投影方法．首先，将问题(1)重新表述为一个基于FB 函数的单调且利普希兹连续的非线性方程组．然后，结合线搜索方案[12]和多元谱梯度投影方法[13]以及改进谱梯度投影方法[11]，对得到的单调非光滑系统提出了一种新修正谱梯度投影方法，并对所提出的方法建立了全局收敛性．通过数值算例，表明了所提出算法的有效性.

本文符号说明如下:‖·‖记为欧几里得范数,〈·,·〉记为欧几里得内积,(·)T记为向量或矩阵的转置,[n]∶={1，2，…，n}.

1 等价非线性方程组的建立

为了便于建立和分析本文的主要结果，先给出如下定义.

(x-y)T(f(x)-f(y))≥0.

(xi-yi)(fi(x)-fi(y)) ≥0,∀i∈[n].

‖F(x)-F(y)‖ ≤L‖x-y‖.

(b) 问题(1)中的fi(i∈[n]) ，存在一个正常数L满足

|fi(x)-fi(y)|≤L|xi-yi|, ∀x,y∈Rn.

设

F(x)∶=x+f(x)-g(x),

(2)

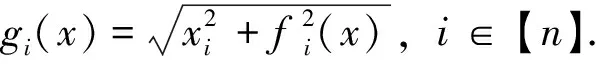
定理1若f(x) 是一致P0-映射，则式(2)定义的F(x) 是单调的.

证明 对于所有x，y∈Rn，i∈[n]，考虑以下两种情况.

若xi=yi=0，显然有(xi-yi)(fi(x)-Fi(y))=0.

若xi≠0 或yi≠0，则有

可得

和

根据假设条件，有

和

(xi-yi)(fi(x)-fi(y)).

因此，有

(xi-yi)(fi(x)-Fi(y))=(xi-yi)[(xi+fi(x)-gi(x))-(yi+fi(y)-gi(y))]=

(xi-yi)2+(xi-yi)(fi(x)-fi(y))-(xi-yi)(gi(x)-gi(y))=

由上述证明，有

证毕．

定理2若fi(x)满足假设1，那么由式(2)定义的F(x)是利普希兹连续的.

证明 对于任意的x，y∈Rn,i∈[n],令u=(xi，fi(x))T,v=(yi,fi(y))T,e= (1,1)T，则有

φFB(xi，fi(x))=φFB(u)=‖u‖-eTu,

和

φFB(yi，fi(y))=φFB(v)=‖v‖-eTv.

由于fi(x)满足假设1，则有

|Fi(x)-Fi(y) |=|φFB(u)-φFB(v) |=

|‖u‖-eTu-‖v‖+eTv|≤

因此，有

证毕.

根据定理1 和定理2，在假设1 的条件下，求解问题(1) 等价于求解一个基于FB 函数的单调且利普希兹连续的非线性方程组

F(x)=0.

(3)

2 算法

采用许多有效的算法来解决由问题(1) 转化的等价的非线性方程组(3)，如牛顿法、无导数法和梯度法．由于在牛顿法中求解雅可比矩阵及其逆矩阵需要大量的计算工作，因此求解光滑方程组代价是昂贵的．为了减少计算量，无导数法和梯度法是目前比较有效的方法．在本节中，提出了一种新修正谱梯度投影方法(New Modified Gradient Projection Method，简称NMGPM)来解决问题(1)．该方法结合了线搜索技术[12]和多元谱梯度投影方法[13]以及改进谱梯度投影方法[11].

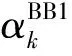
(4)

(5)

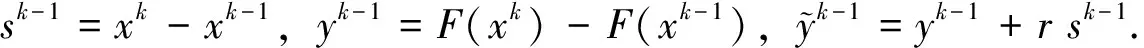
进一步，结合线搜索方案[12]和多元谱梯度投影方法[13]，得出如下算法.

算法1(NMGPM 算法)

步0 给定ε>0,x0∈Rn，设σ,β∈(0,1),α0=1,r∈[0,1],置k∶=0.

步1 若‖F(xk)‖≤ε，停止，并接受xk为近似解.

步2 计算搜索方向

dk=-αkF(xk).

(6)

步3 计算zk=xk+θkdk，其中θk∶=βmk,mk是最小的非负整数使得

-F(xk+θkdk)Tdk≥σγkθk‖dk‖2,

(7)

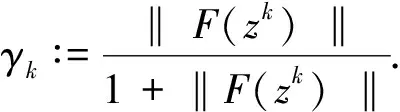
步4 更新迭代

(8)

步5 选取λk∈[0,1]，更新谱向量

(9)

步6 置k:=k+1，转步1.

下面引理说明算法1适定.

引理1在假设1 下，对于所有的k≥1 ，存在一个非负数mk满足算法1.

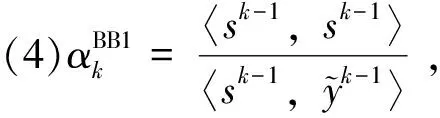
(10)

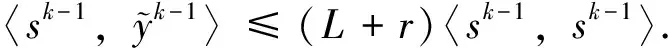
(11)

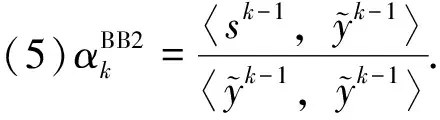
(L2+Lr+(L+r)r)〈sk-1，sk-1〉=(L+r)2〈sk-1，sk-1〉.

由αk的定义式(9)，可得

(12)

下面用反证法证明结论．假设存在k0≥1 使得式(7)不满足任意的非负整数m，即

-〈F(xk0+βmdk0) ，dk0〉<σγk0βm‖dk0‖2.

-〈F(xk0) ，dk0〉 ≤0.

(13)

然而，由dk的定义式(6)和式(12)，有

(14)

这与式(13)矛盾.证毕.

3 全局收敛性

引理2[14]设F(x) 是单调的，且x，z∈Rn使得F(z)T(x-z)>0．设x*为F(x)=0 的一个解并且

那么有

‖x+-x*‖2≤ ‖x-x*‖2-‖x+-x‖2.

定理3在假设1下，设序列 {xk} 由算法1 生成，且ε=0，则有

证明 根据假设1，f(x) 是一致P0-映射，所以F(x) 是单调的．由算法1 中的式(7)，有

F(zk)T(xk-zk)=-βmkF(zk)Tdk≥σγkβmk‖dk‖2>0.

由引理2 有

‖xk+1-x*‖2≤‖xk-x*‖2-‖xk+1-xk‖2,

(15)

其中x*是F(x)=0 的解．因此，{ ‖xk-x*‖ } 是一个递减序列．对于所有k≥1，有‖xk-x*‖ ≤ ‖x0-x*‖，意味着 {xk} ⊂{x∈Rn：‖x-x*‖ ≤ ‖x0-x*‖ }．因此， {xk} 是一个有界序列．因为F(x) 是连续的，{ ‖F(xk) ‖} 是有界的.

(16)

由式(16)， {dk} 也是有界的且 {zk} 也是有界的．因此，存在常数M>0 使得对于任意的k，有 ‖F(zk) ‖ ≤M．

由式(15)，有

(17)

由式(8)，有

定理4在假设1下，设序列 {xk} 由算法1 生成，且ε=0， 则序列 {xk} 收敛到某个点x*使得F(x*)=0.

证明 由定理3，有

(18)

由算法1和式(12)，有

(19)

由式(16)， {dk} 是有界的．下面分两种情况证明.

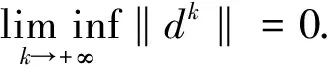
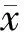
当

由式(19)，有

由式(18)，可得

由算法1 ，有

-〈F(xk+βmk-1dk) ，dk〉<σγkβmk-1‖dk‖2.

(20)

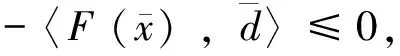
(21)

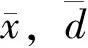
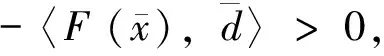
4 数值实验

为了测试所提出的NMGPM方法的数值性能，本节给出了一些初步的数值结果.

首先讨论凸组合系数λk的选择，并为数值实验做了准备．最简单的方案是在所有迭代中固定λk，即在[0,1] 内选择一个常量作为λk的值．对于所有的k，分别设置λk=0.1，0.3，0.618和0.9．实验中则选择实验效果最好的λk作为最后的结果.

将算法1 与多元谱梯度投影法(简称MSGP)[13]和改进的梯度投影法(简称MGP)[15]进行了比较.在MATLAB R2018a软件上进行数值实验．若 ‖F(xk)‖ ≤10-5，则终止运行.

算法参数设置如下：

(1) 对于MSGP算法，设置ρ=0.5，σ=0.001，=10-10，r=0.01,

其中τ=10-8，且

(3)对于NMGPM算法，设置α0=1,β=0.618,σ=0.01,r=0.001．

所有的实验起始点为x0=rand(n，1)，实验结果为5 次实验的平均值.

下面给出具体实例.

例1函数f(x)的组成部分描述如下

fi(x)=ln(xi)-sin(|xi-2|)，i∈[n].

例2函数f(x)的组成部分描述如下

fi(x)=exi-1，i∈[n].

例3函数f(x)的组成部分描述如下

例4函数f(x)的组成部分描述如下

例5函数f(x)的组成部分描述如下

fi(x)=2xi-sin(|xi|)，i∈[n].

例6函数f(x)的组成部分描述如下

fi(x)=xi-sin(|xi-1|)，i∈[n].

例7函数f(x)的组成部分描述如下

表1给出了例2-7的数值结果.

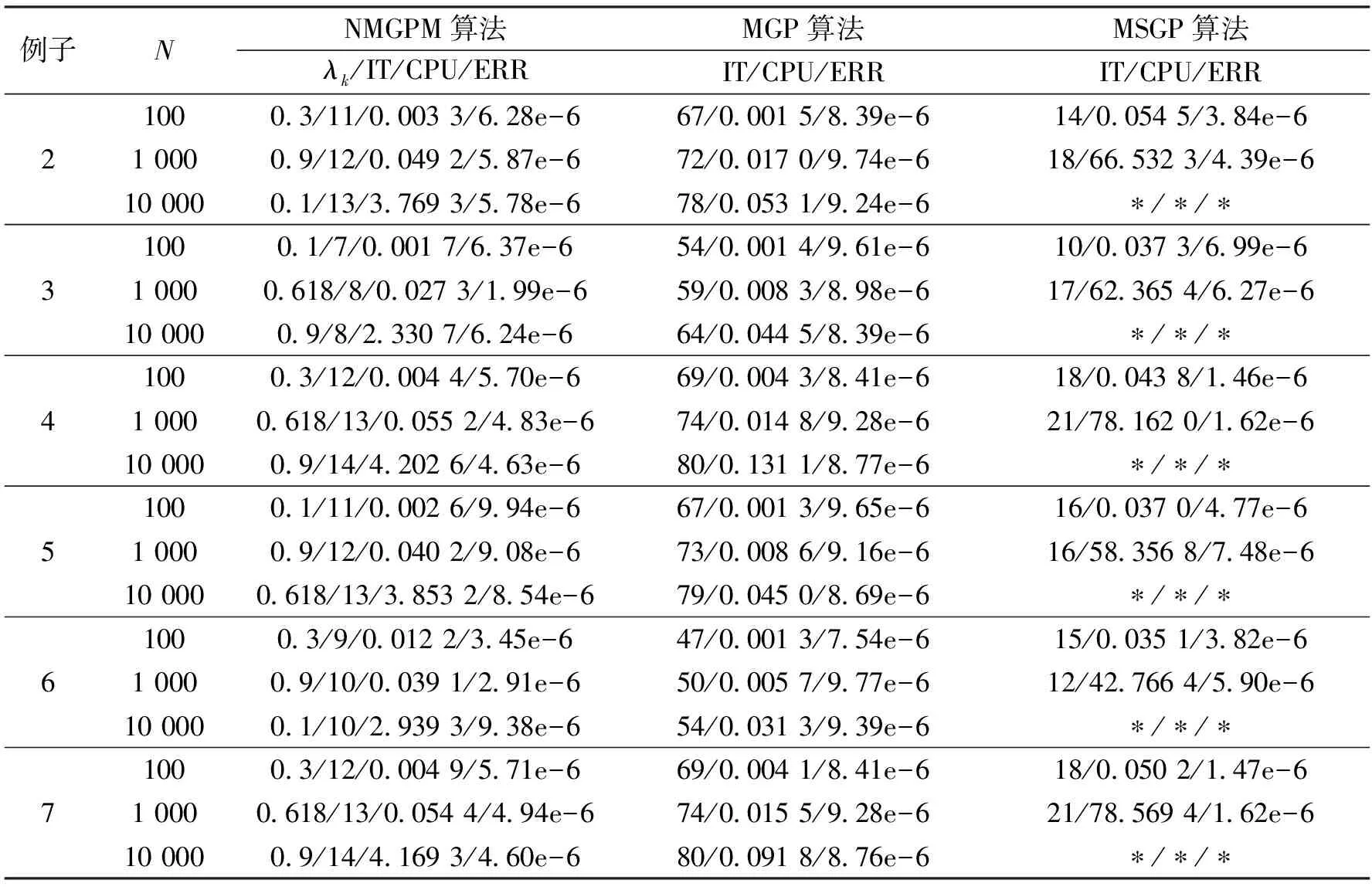
表1 例2-7的数值结果Tab.1 The numerical results for examples 2-7

图1 例1中λk与IT关系图Fig.1 The relationship between λk and IT for example 1

图1给出了例1的数值结果.λk的取值会影响NMGPM算法的迭代次数，对算法的数值性能产生影响，因此需要选择适合的λk.

数值结果表明，对于例2-7，所提出的NMGPM方法与MSGP方法相比，在CPU 时间上有明显的改进，因为MSGP方法中需要对谱梯度αk的每个元素进行赋值，需要花费一定的时间.而NMGPM方法直接对αk进行整体的赋值，花费的时间更少.3 种方法中MGP方法使用的时间最少，原因是NMGPM方法有MGP方法中没有的线搜索技术，在线搜索步中寻找mk的过程需要花费一定的时间.MSGP方法在阶数为10 000时没有结果，原因是算法运行过程中对谱梯度αk的每个元素进行赋值，阶数越高花费的时间越多，在阶数为10 000时需要花费超过1 000 s的CPU时间.

在迭代次数方面，所提出的NMGPM方法的次数最少，与MSGP方法比较相差较小，与MGP比较有明显的减少．并且NMGPM方法的迭代次数在实验阶数10 倍增长的情况下没有明显的增长,原因是NMGPM方法使用一种新的线搜索方法，找到了3 种算法中最优的下降方向,因此NMGPM方法的迭代次数最小.

在误差方面，3 种方法都达到了终止条件中的要求，无明显差别.

总体来说，NMGPM 方法在CPU 时间和迭代次数上都有良好的表现，尤其在迭代次数上有明显优势，该算法对于求解非线性互补问题是有效的.

5 结论

本文将非线性互补问题重新表述为非线性方程组，并研究了一定假设条件下，得到的非线性方程组中映射的单调性与利普希兹连续性．在此基础上，提出了一种新修正的谱梯度投影方法来求解NCP，并建立了该方法的全局收敛性．与原来的多元谱梯度投影方法相比，所提出的NMGPM 算法中谱向量的更新方案成本更低，线搜索规则提高了数值性能．与改进的梯度投影法相比，所提出的NMGPM 算法具有更少的迭代步数，新的线搜索规则发挥了很大作用．初步的数值结果表明，该方法优于现有的一些方法，对于求解非线性互补问题是有效的．然而，所提出的NMGPM 算法中λk的选择还有待进一步改进，若能找到最优的λk，相信算法的性能会有更好的表现.