表面介质阻挡放电起始演化过程研究

孙伟铭

重庆大学输配电装备及系统安全与新技术国家重点实验室 重庆 400044

引言

表面介质阻挡放电（surface dielectric barrier discharge，SDBD）在航空航天、流动控制领域有广泛的应用前景[1-5]。SDBD激励器应用于机翼表面能产生沿表面发展的放电通道，产生离子风，诱导气流的发展，减少阻力、增加升力[6-7]，故了解SDBD的放电通道发展过程对其在流动控制方面的应用有重要意义。

近年来，很多学者致力于SDBD通道发展过程的仿真研究，得到不同的结果。如Boeuf等研究SDBD发展过程中发现，放电通道在高压电极上边缘激发，以类似半圆轨迹沿介质表面发展[8]；Peng等也发现放电通道起始于高压电极上边缘，在发展过程中放电通道未完全附在介质表面[9]；而Zhu等研究得到不同的结果，发现放电通道在高压电极下边缘激发，紧贴介质表面发展[10]；此外，Chen等得到与Zhu等类似的结果[11]。对比上述学者的研究成果发现，SDBD的放电起始位置不同导致放电通道的起始发展方向不同，影响放电通道的演化路径。当放电通道在高压电极上边缘被激发时，放电起始发展方向为右上方，使通道在演化过程中未完全附在介质表面；当放电通道在高压电极下边缘激发时，放电沿介质方向并紧贴介质表面发展，因此放电的起始位置决定了放电初始发展方向[12]，影响放电通道演化路径。放电通道的起始位置由SDBD起始演化过程决定，目前针对SDBD起始演化过程的报道相对较少，故开展SDBD起始演化过程的研究对放电通道的演化路径的理解有重要意义。

因此，本文构建了二维仿真模型，对SDBD的放电演化过程展开研究，分析放电起始位置的影响因素。

1 数值模型

1.1 几何参数

本研究基于COMSOL Multiphysics软件建立了二维仿真模型，如图1所示。阻挡介质为环氧树脂，其相对介电常数εr为2.4，厚度为1mm。高压电极在介质的上表面，长度为0.5mm，厚度为0.05mm。高压电极的右上角做圆角处理，曲率半径为0.05mm。地电极位于阻挡介质的另一侧，在模型中地电极被等效为2mm的线段以降低计算难度。高压电极右边缘与地电极的左边缘对齐，即电极之间的水平间距为0mm。x、y轴如图1所示，将高压电极右下角端点定义为O(0,0)，电极上边缘的点(-0.033,0.047)定义为P0。

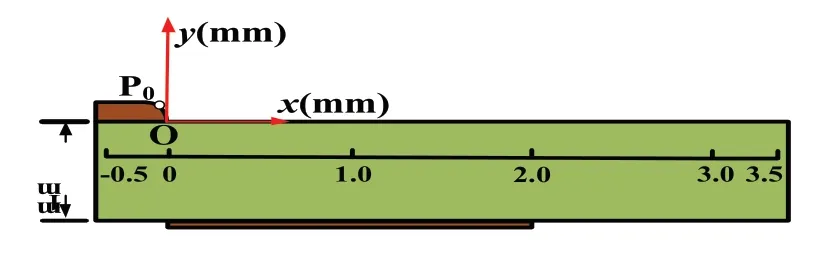
图1 SDBD的二维仿真模型

1.2 控制方程

仿真模型中涉及的控制方程包含粒子连续性方程、电子能量守恒方程和泊松方程。忽略电子对流的影响，粒子连续性方程表示为：

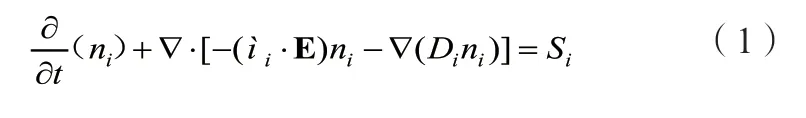
式中：ni为粒子i的数密度，包含电子、离子和中性粒子；μi和Di分别为粒子i的迁移率和扩散系数；E为电场；Si为粒子源项，表示反应中粒子生成量与消耗量的净值，表示为：

Ci,r和Ri,r分别为反应r中粒子i的化学计量常数和反应速率。

电子能量大小受电场强度的影响，直接决定电子与中性粒子之间碰撞速率大小，是研究放电发展的重要参数。电子能量守恒方程为：

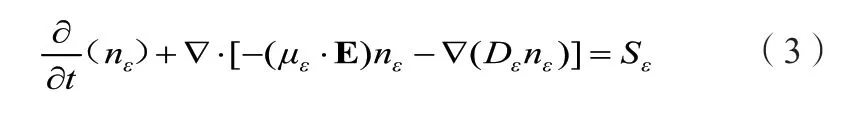
式中：nε为电子能量密度；με和Dε分别为电子能的迁移率和扩散系数；Sε为电子能量源项。

电子迁移率μe、电子扩散系数De、电子能迁移率με和电子能扩散系数Dε满足爱因斯坦方程：

式中：Te为电子温度，泊松方程用以计算电场和电势。

式中：V为电势；ε0和εr分别为真空中的介电常数、相对介电常数；ρq为空间电荷密度。

1.3 边界条件及化学反应

求解域的所有外部边界设置为零电荷条件，表达式为:

因在放电过程中介质表面有电荷沉积，介质表面的边界条件设置为表面电荷积累：

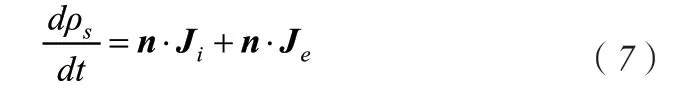
其中，ρs为表面电荷密度，n·Ji、n·Je分别为沿法线方向的离子电流分量和电子电流分量。阻挡介质设置为电荷守恒。

空气作为一种混合气体，包含几十种粒子，涉及数百个化学反应[13]。本模型主要对SDBD的起始过程进行研究，而非分析具体粒子的时空演化规律，因此用反应集代替复杂的反应以降低计算难度。化学反应集如表1所示，涉及电离、附着、复合反应等。反应集中涉及的中性粒子用A表示，发生电离产生的正离子和附着反应生成的负离子分别用p、n表示[14]，e为电子。

表1 模型中的反应

1.4 计算区域与初始值

模型的计算区域包含放电区域与介质区域，计算区域的宽度为4mm，与介质的宽度一致，高度为2.5mm。计算域的网格剖分情况如图2所示，由于介质表面不仅存在粒子间的反应，还涉及表面反应，故对介质表面的网格加密。在模型中最大网格单元为16μm，最小网格单元为2μm，调试结果与[15]保持在同一量级。

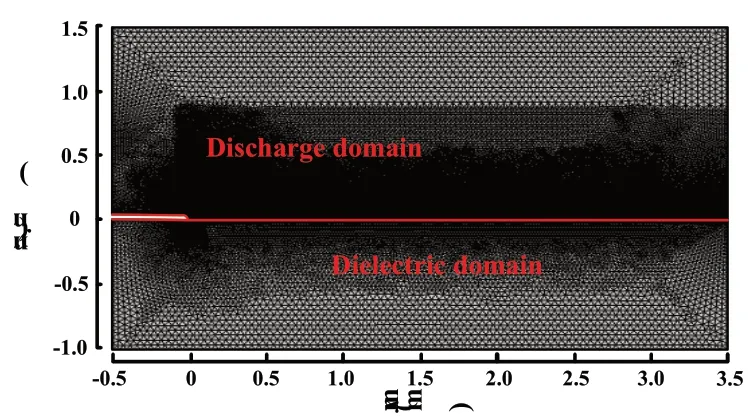
图2 模型的网格剖分结果

初始气体温度为293.15K；气体压强为760托；驱动电压为正极性三角脉冲波，上升时间和半高宽分别为70ns与100ns，幅值为9kV，如图3所示；介质的介电常数为0.24；介质表面的二次电子发射系数为0.01；初始电子密度为3×1010/m3[16]，为使空气在初始条件下处于电中性，带电粒子密度设置为3×1010/m3。

图3 正极性三角脉冲波

2 结果与讨论

计算得到的放电通道演化路径如图4所示，在高压电极施加高压脉冲时气隙中会产生电离波，在电离波的影响下通道起始于高压电极的上边缘并沿介质发展，与Peng等的结果相似。对放电阶段的划分，即将0-t0作为放电起始阶段，t0为放电起始时间，由于9ns时放电通道已激发，故t0＜9ns。因放电起始位置是放电时通道在电极表面被激发的位置，故研究放电起始位置前需先对放电起始时间t0进行判定。

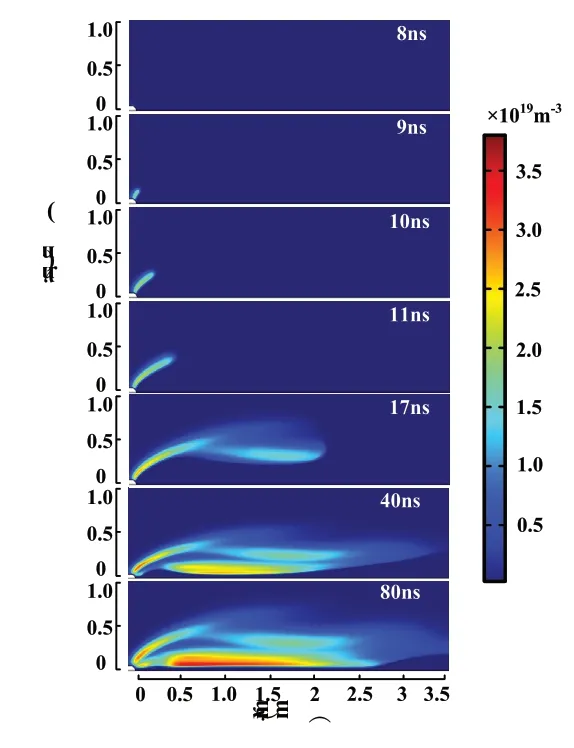
图4 不同时刻下空间电子数密度分布

2.1 放电起始时间

在以往的研究中，对SDBD放电时间的判定主要依据放电电流[17]。放电电流由两部分组成，位移电流与传导电流，即：

it为放电电流；id为位移电流，位移电流不是电荷定向移动形成的电流，而是电位移矢量对时间的偏导数，即ic为传导电流，其大小与电场力作用下发生定向移动的电荷相关，具体数值通过高压电极表面的电荷通量Q对时间t的偏导数计算，即

传导电流的变化不是瞬时性的，而是在放电通道形成过程中逐渐增大，因此从放电电流角度对放电时间进行判断与实际放电时间会存在偏差。放电通道形成会使电场分布发生畸变[18]，而放电通道从电极表面激发，因此从电极表面的电场分布开展对放电起始时间的研究。

图5所示为5~8ns时刻高压电极表面的电场强度分布，x为对应位置的横坐标。结果表明，因放电结构的缘故，电极表面的电场分布不均匀，电场随x增大而增强，最强电场在x=0mm的O点取得。8ns之前，随着电压增大，电极表面的电场整体增强。8ns时电极表面的电场强度分布发生改变：在-0.5mm＜x＜-0.05mm，电场随x增大减弱至0.04kV/cm；在-0.05mm＜x＜-0.022mm，电场随x增大呈先增强后减弱的变化趋势，形成电场强度分布曲线“上凸”，在x=-0.033mm处电场强度取得3.25kV/cm的极大值点；当-0.022mm＜x＜0mm时，随着x增大，电场逐渐增强，8ns时在O点处电场最强，为91.3kV/cm。

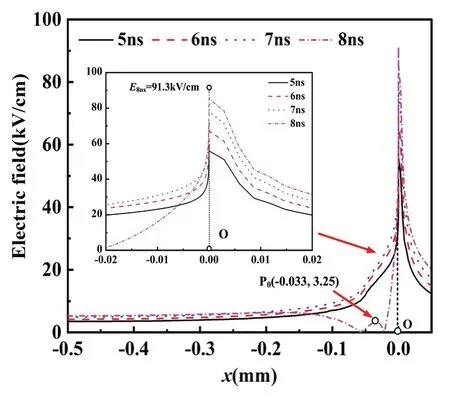
图5 不同时刻下高压电极表面的电场分布

8ns时电极表面电场分布发生畸变，其原因为从电极表面激发的放电通道等同于高压电极的延伸[19]，可视为电极表面的形貌改变，放电位置处出现“凸起”，此时的结构与锯齿有些相似。由于锯齿尖端的放电要强于两侧[20]，即电场在尖端更强。因此，放电通道的形成会使放电位置附近的电场分布出现“凸起”的特性。

为验证上述结论，对放电时的放电通道等效，绘制如图6（a）-（b）所示的草图，对其电场进行仿真，（a）、（b）分别为未放电、放电时的SDBD结构。由于本过程旨在了解通道的激发对电极表面电场的影响，因此对放电通道的几何等效并未严格按照通道演化结果绘制。选用圆心在（-0.025,0.035），半径为0.01mm的圆被电极表面截取部分，模拟刚从高压电极表面被激发通道的二维界面。因放电通道内部的电导率很高，忽略通道内部的阻抗，将其等效为导体。高压电极、地电极、阻挡介质等参数与2.1中模型的几何参数保持一致，高压电极上施加的电压8ns时的电压900V，电极表面电场分布的仿真结果如图6（c）所示。

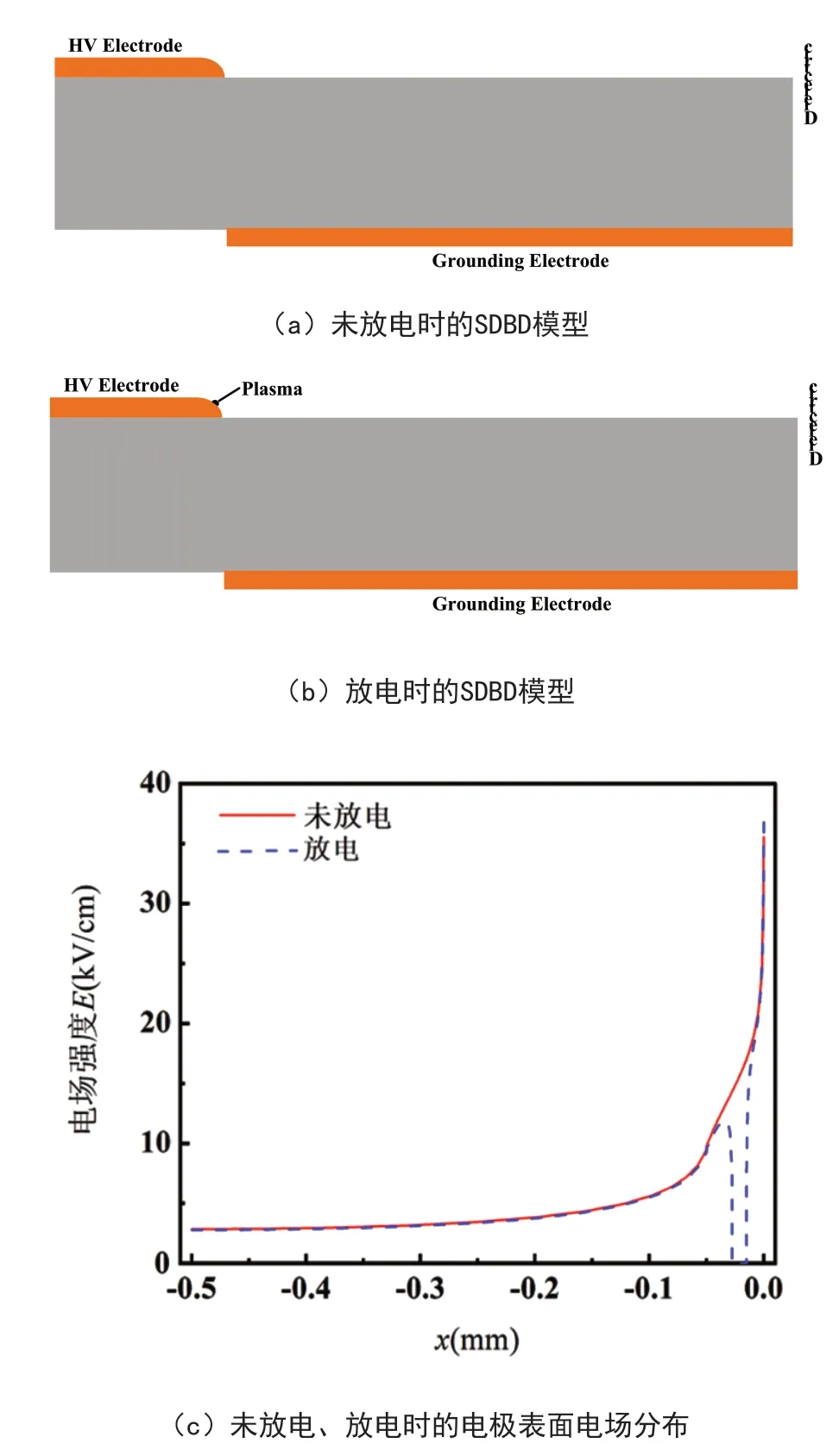
图6 放电通道的激发时高压电极表面电场分布

电极表面电场分布的仿真结果如图6（c）所示，结果表明，当有放电通道从高压电极表面激发时，电极表面的电场分布发生畸变，电场分布曲线会出现一个“凸起”，与图5中8ns时高压电极表面的电场分布曲线对应，验证了前文中提出的结论。由于对放电通道的等效忽略了其内部阻抗，因此在出现“凸起”后电场强度迅速减弱，电场结果与图5中的8ns时电极表面电场分布存在略微的偏差。

2.2 放电起始位置

放电通道的起始位置直接决定放电初始发展方向，影响通道从高压电极发出后短时间内的演化路径[21]，是研究放电起始过程的重要因素，但目前有关放电起始位置的深入研究鲜有报道。在电子数达到一定数量时发生放电[22]，即放电位置处的电子数达到最大，故通过对高压电极表面电子数密度分布进行分析来展开对放电位置的研究。

图7所示为6~9ns时高压电极表面的电子数密度分布，6ns时电压很低，电场强度弱，导致电离过程产生的电子数少，故电极表面的电子数密度曲线紧贴x轴。在7ns-8ns，随着电压增大，电场增强，产生的电子数更多，使高压电极表面的电子数整体增多，8ns时在高压电极表面x=-0.033mm的对应位置处电子数密度达到最大，为1.01×1018/m3，与Kourtzanidis[23]中的结果相近。9ns时，高压电极表面的最大电子数密度相较于8ns时有所减小。这是由于在放电未从高压电极演化出时，碰撞电离过程最强的区域位于放电起始位置附近，当放电通道向外演化后，在流注头部的电离程度最强[24-25]，这也印证了2.1节中对放电时间的判断。

图7 不同时刻下高压电极表面的电子数密度分布

对比5~8ns电场强度在电极表面的分布规律发现，在放电通道形成过程中，电场一直在高压电极右下角的点O（0，0）处最强。然而，放电通道却发生在高压电极上边缘的P0（-0.033，0.047），这与电场较强的地方更易激发放电这一规律相悖。

对此，结合气体放电的本质解释，气体放电是由电离过程引起，其中碰撞电离占主要部分，碰撞电离与参与的电子数、电场强度均呈正相关[26]。图8所示为未放电时的电场分布矢量，假设在未施加电压时，空间中的电子进行热运动均匀分布。施加电压后，空间中的电子在电场的作用下沿着电场线的反方向朝高压电极运动，在阳极表面附近发生碰撞电离。因此，从高压电极表面各位置发出的电场线，在空气中长度与运动至该位置处的电子数呈正相关，各位置的电场强度决定了电子发生碰撞电离的概率。结合图7中8ns时的电子数密度分布和图8所示的电场线可知，虽然O点的电场强于P0点，但运动至P0处的电子数远高于O点，因此放电起始于P0。

图8 未放电时的空间电场矢量分布

3 结束语

本文研究了不同时刻下高压电极表面的电场强度分布，判断出放电起始时间。此外，还通过对不同时刻下高压电极表面的电子数密度分布进行研究，分析了放电起始位置，并对放电起始位置进行了解释，得出以下结论：

SDBD结构发生放电时，高压电极表面的电场分布会发生畸变，放电位置附近的电极表面电场强度曲线会出现“凸起”的特征。这是由于发生放电时，放电通道的激发可视为高压电极的延伸，等效于电极表面形貌的改变，此时与锯齿电极有些相似。由此可通过电极表面电场分布曲线出现“凸起”的特征来判定放电起始时间。

SDBD的起始位置与常见的针板电极结构的放电位置不同，针板电极结构的放电发生在电场最强的尖端，而SDBD的起始位置在电场较弱的P0点，并非电场最强的O点。这是因为放电主要受碰撞电离过程的影响，碰撞电离是电子在电场作用下沿电场线的反方向运动，并在高压电极表面发生碰撞电离，因此碰撞电离程度与参加电离的电子数和电场强度均呈正相关。假设在未施加电压时，空间中的电子进行热运动均匀分布。当施加电压时。汇集于P0、O两点的电子数正比于从P0、O两点发出的电场线在空气中的长度，据图7可知P0点处聚集的电子数远大于O点，因此在P0点处发生放电，而非O点。