基于贝叶斯网络的重载汽车液力变矩器可靠性分析

林昊 佟维妍

沈阳工业大学化工过程自动化学院 辽宁 辽阳 111000

引言

液力变矩器是重载汽车的核心部分，其工作时能够让重载汽车在行驶过程中免于车体振动或转动影响一直处于水平向和垂直向位置上。同时，它能够在各种恶劣环境下，实现增大力矩，在保证速度的同时还能够让重载汽车实现无级变速。所以，液力变矩器的好坏决定了重载汽车的运行能力。

由于液力变矩器本身结构复杂，对其进行可靠性分析十分必要。但是目前液力变矩器的可靠性分析停留在系统和部件各类性能指标上，且依靠技术人员的知识和经验，过于主观。因此，本文提出了一种以主观经验为辅的可靠性分析方法——模糊贝叶斯网络，对重载汽车中的液力变矩器进行可靠性分析。

1 理论知识

1.1 可靠性分析基本知识

近年来，随着世界各国对可靠性分析的重视，各国政府在可靠性分析上投入了大量时间和精力进行研究，最终应用到各个技术领域。可靠性分析按时间可大致分为萌芽阶段、普及阶段、成熟阶段：①萌芽阶段：该阶段可追溯到20世纪30至40年代。因此，人们在电子设备上率先进行了可靠性分析。②普及阶段：到了60年代，可靠性分析已经从电子、工程等领域逐步扩展到各个领域，也从军事行业逐步转到了民用领域。到了70年代，可靠性分析在国际上受到广泛的关注，并向着国际的趋势发展[1]。③成熟阶段：从80年代开始，可靠性技术的影响已经非常的广泛，继而向着更深层次更广泛的应用方向去研究。进入90年代，可靠性分析工作逐渐加深，并与维修性相结合。

可靠性分析常用的方法有：马尔科夫过程分析法、蒙特卡洛分析法、贝叶斯网络方法等。①尔科夫过程分析法：马尔可夫过程是由俄国数学家马尔可夫将概率论与统计与可靠性分析相结合提出来的方法，该方法主要通过研究系统的“状态”与“状态”之间相互转移对系统进行可靠性分析。1992年J.B. Dugan教授以空间站和空中交通管理等系统为研究背景，将Markov理论和组合数学应用到一起，构建了基于Markov故障树模型。②尔科夫过程分析法：马尔可夫过程是由俄国数学家马尔可夫将概率论与统计与可靠性分析相结合提出来的方法，该方法主要通过研究系统的“状态”与“状态”之间相互转移对系统进行可靠性分析。1992年J.B. Dugan教授以空间站和空中交通管理等系统为研究背景，将Markov理论和组合数学应用到一起，构建了基于Markov故障树模型。③贝叶斯网络：贝叶斯网络继承了故障树的特点和优点，通过搭建有向无环图对设备进行可靠性分析。近些年经过众多专家、学者的完善以及数学和各种算法的发展使其成为对系统进行可靠性分析的重要和核心方法[2-3]。

1.2 贝叶斯网络

贝叶斯网络（BN），又称信度网络。BN通常以变量的节点及把连接这些节点的有向边组合在一起形成一有向无环图（DAG）的形式出现。其中，随机变量就是DAG的所有节点，如果两个或更多个节点有一定关系，则将他们用单向箭头连接起来，它们之间的密切程度用条件概率表（CPT）表示。因为节点是各种抽象变量的载体，所以无论是否有控制因素的存在，无论这些节点对应的变量是离散的还是连续的，BN都可以准确地描述和处理它们所对应的不确定概率性问题，也可以从这些模糊、缺失或不确定的知识或数据中进行正反推理。

设M=（A,B）是一有向无环图，其中字母A表示所有节点的集合，B表示有向无环图的集合，令X=为图形节点i代表的随机变量，则其联合概率分布为：

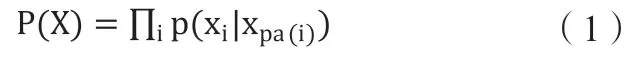
式中，X为M的一贝叶斯网络，节点i的原因由pa(i)表示。

1.3 模糊贝叶斯网络

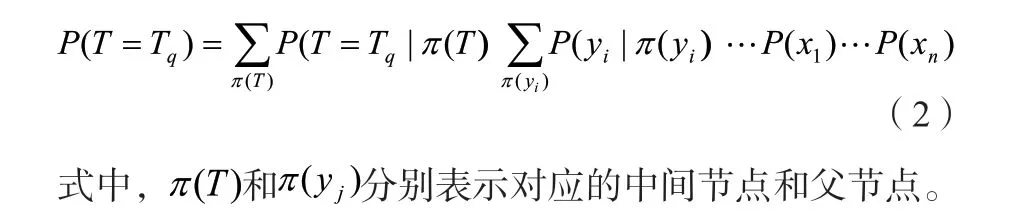
1.3.2 父节点的确定。本文引入{非常低（VL），低（L），偏低（ML），中等（M），偏高（MH），高（H），非常高(VH)}这七种自然语言变量作为模糊贝叶斯网络中父节点的故障率，具体含义如表1所示。

表1 事件发生的语义值及相应的三角模糊数

将表1中的数据与专家权重相乘，得到模糊概率，其公式如下：

最后解模糊，设通过公式3得到的结果为[a，b，c]，解模糊得：

2.4 可靠性分析

计算后验概率，目的是在系统发生故障后，求出各基本事件发生的故障率，从而对系统的父节点进行可靠性分析，对提高系统的可靠性具有实际的意义。

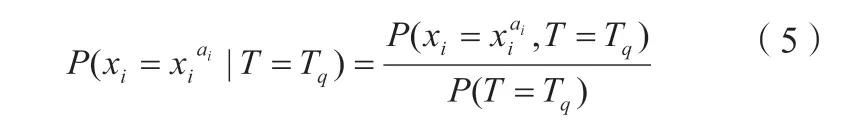
3 实例仿真

由于液力变矩器过于复杂，因此本文仅对重载汽车中的液力变矩器进行可靠性分析。通过专家经验法搭建液力变矩器的模糊贝叶斯网络，其结构如图1所示。

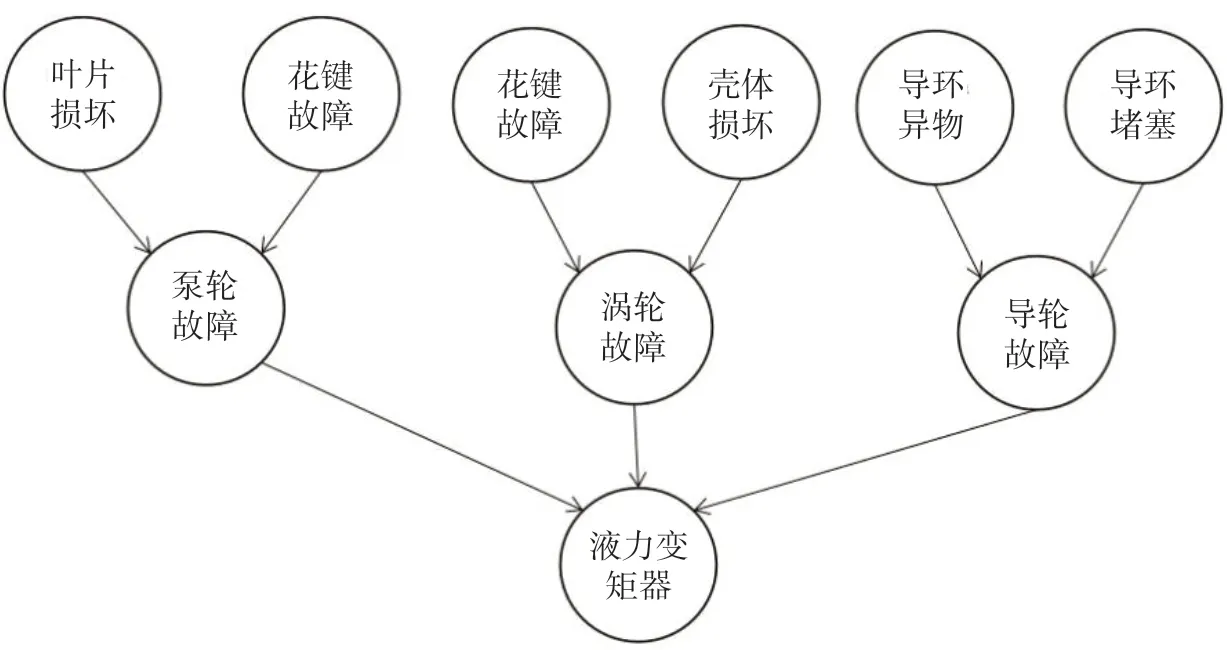
图1 半自动工况下工作下贝叶斯网络

将表1、公式3和公式4相结合得到模糊贝叶斯网络其结果如图2所示。

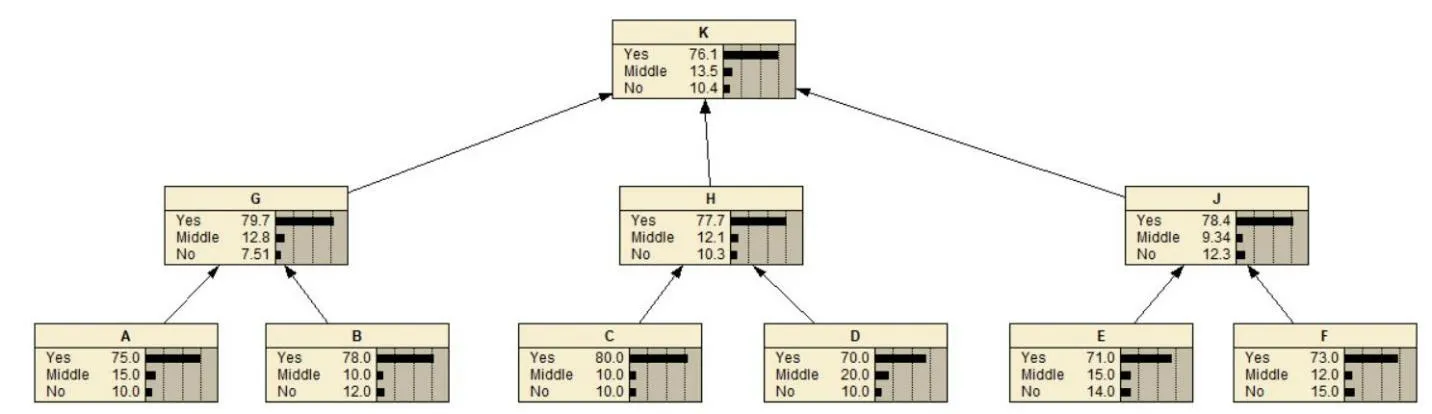
图2 子节点的故障率

图2中，字母A到字母K分别表示叶片损坏、泵轮花键故障、涡轮花键故障、壳体损坏、导环异物、导环堵塞、泵轮故障、涡轮故障、导轮故障、电机放大机、液力变矩器。Yes、middle和No分别表示无故障、轻微故障和完全故障三种情况下的故障率，从图可知，当该系统轻微故障率是0.135，完全故障是0.104。

4 结束语

由公式5可以计算出该系统的后验概率，之后对液力变矩器的工况系统进行可靠性分析，得到以下结论：

当系统处于轻微故障时，其后验概率排序为A＞D＞E＞C＞F＞B。由此可知，系统处于轻微故障时，泵轮叶片易损坏、涡轮壳体易损坏和导环出现异物。因此，在短时工作时要注意对上述三种设备进行定期检修和维护。

当设备处于完全故障时，其后验概率排序为C＞E＞A＞D＞F＞B。由此可知，系统处于完全故障时，涡轮花键易故障、导环有异物和泵轮叶片容易故障。因此，在长时间工作时要注意对上述三种设备进行定期检修和维护。