电力系统振荡对距离保护影响的仿真分析

纪静，梁毅

（1.重庆邮电大学，重庆，400065；2.华为技术有限公司，广东深圳，518129）

0 引言

距离保护由于其稳定性好、灵敏度高等优点，被广泛应用于输电线路继电保护中。当电力系统中出现输电线路输送功率超过极限值造成静态稳定破坏，或者电网发生短路故障，切除大容量的发电、输电或变电设备，负荷瞬间发生较大突变等造成电力系统暂态稳定破坏时，都将引起电力系统振荡[1]。此时，有可能造成距离保护的误动。因为振荡时由于功角的周期性变化，系统中各点的电压、线路电流、功率大小和方向以及距离保护的测量阻抗均会呈现周期性的变化[2]，从而造成保护误动。振荡现象自电网建设以来就没有得到真正解决，虽然这不是故障，但其带来的危害有时会比短路更为严重。

本文通过仿真分析研究电力系统振荡对线路距离保护的影响，并对振荡闭锁以及振荡过程再故障的解决方案进行建模仿真。

1 电力系统振荡时的电气量特点

■ 1.1 振荡的概念

电力系统振荡是指发生在电力系统或发电厂间、功率角出现在0～360°之间大幅度周期性摆动的现象。电力系统振荡属于系统的不正常运行，因而一般输电线路上都会配备有自动调节恢复装置，当振荡发生时能够自行调节、稳定振荡。但振荡可能会造成保护误动，切除重要的输电线路，造成严重后果[3]。

■ 1.2 电力系统振荡时电压、电流的特点

图1所示是一个简单双侧电源电力系统，设系统两侧的等效电动势和幅值相等，相角差为δ，两侧电源间总阻抗为Z∑=ZM+ZN+ZL，ZM、ZN分别为M、N两侧系统的等值阻抗，ZL为输电线路阻抗。

图1 简单双侧电源电力系统

文献[4]给出了该系统母线M和N的电压有效值以及线路中电流有效值的变化曲线，如图2(a)、2(b)所示。由图可见：电压和电流有效值呈现周期性变化的特点。

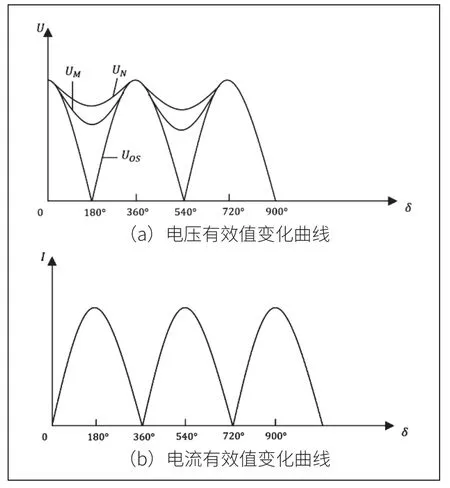
图2 系统振荡时的电压和电流

■ 1.3 电力系统振荡时测量阻抗的特点

当电力系统振荡时，从母线M处测得的测量阻抗为[4]：

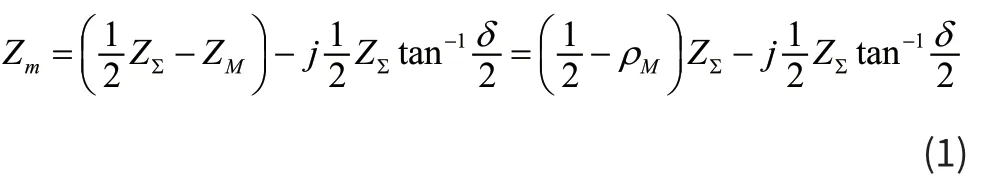
由式(1)可得，当系统振荡时，保护安装处M的测量阻抗由两部分构成：和。为振荡中心到保护安装处的线路阻抗，只与振荡中心到保护安装处的相对位置有关；而第二部分垂直于ZΣ，并随着δ的变化而变化，即测量阻抗也呈周期性变化。

2 电力系统振荡及距离保护的仿真分析

本文以图3所示系统为例进行振荡对距离保护的影响分析。系统两侧电源分别为EM、EN，电压等级为10kV。输电线路设为三段，分别为AB、BC、CD，每一段输电线路两侧都设置有距离保护。输电线路的单位正序阻抗为：Z1=0.21+j0.31Ω/km。

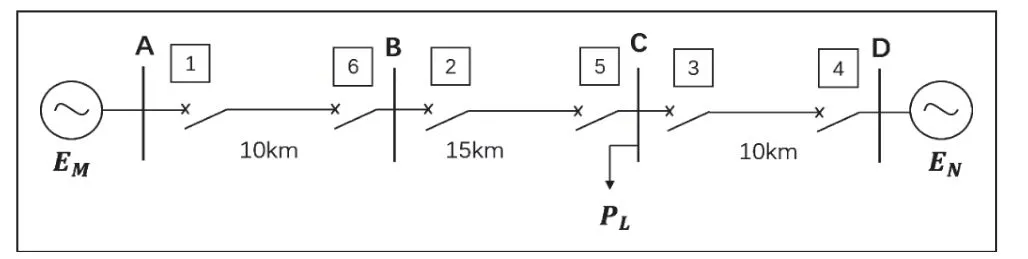
图3 双侧电源系统距离保护算例

为便于分析计算，三段距离保护都选用方向圆特性阻抗继电器。

阻抗继电器有两种接线方式：0°接线方式和带零序补偿的接线方式[5]，发生相间短路时用0°接线方式，发生相地短路时用带零序补偿的接线方式，本文将两种接线方式相配合，即可实现完整的距离保护。

为了模拟系统振荡，在图3所示系统中设置电源EM的频率fM为50Hz，EN的频率fN为55Hz。测量母线A处的电流，如图4所示。当系统发生振荡时，测量保护1处的测量阻抗变化情况，如图5所示。

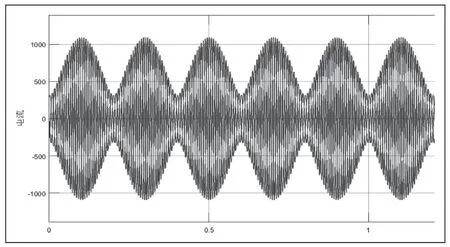
图4 电力系统发生振荡时母线A处的电流波形

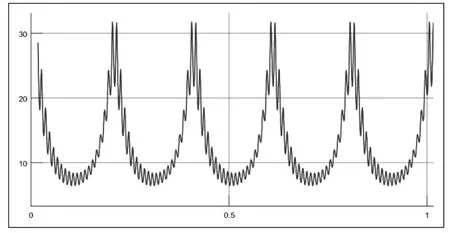
图5 系统振荡时测量阻抗的变化波形

由图4可见：系统振荡时，电流幅值发生了周期性变化。由图5可见：系统振荡时，测量阻抗出现很大的周期性波动，从而可能在某个时刻低于整定阻抗，进入保护动作区，造成保护误动。

图6是系统振荡时阻抗继电器的动作信号波形，1表示继电器动作，可见，阻抗继电器出现了周期性地动作和返回，即距离保护出现误动。

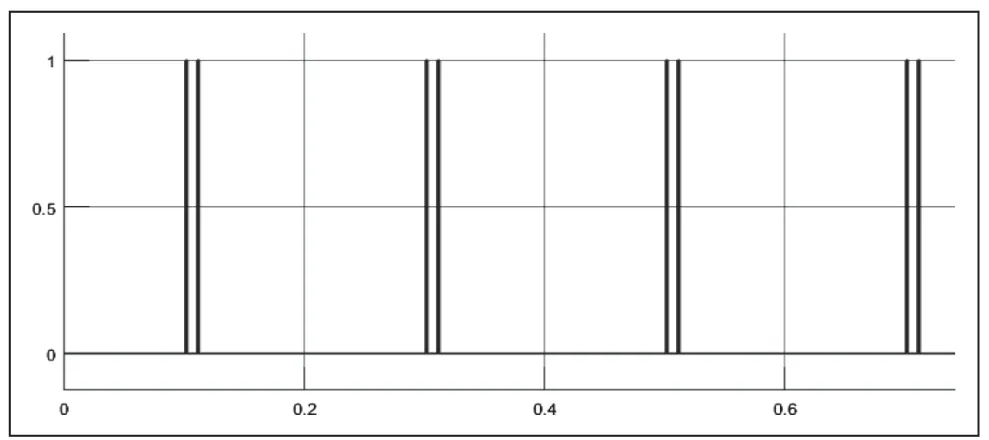
图6 振荡时阻抗继电器的动作信号波形

3 振荡闭锁措施及再故障的解决方案

■ 3.1 振荡闭锁措施

由上文分析可知，系统振荡会导致距离保护误动，因此，实际系统应增加振荡闭锁措施。由于在电力系统发生短路时，测量阻抗Zm由负荷阻抗ZL突变为短路阻抗Zk，变化速度很快；而在振荡时，测量阻抗Zm由负荷阻抗ZL慢慢变成振荡中心到保护安装处的线路阻抗，其速率与δ的变化速率一致[4]。因此，本文利用测量阻抗变化速率的不同构成振荡闭锁元件。

增加振荡闭锁元件以后，仿真结果如图7所示。在系统发生振荡期间，即使阻抗继电器的动作条件能够满足，振荡闭锁元件判断出这并不是故障，即不开放保护，因此，保护不会误动。

图7 电力系统振荡时继电器的动作信号波形

■ 3.2 振荡过程再故障的解决方案

当振荡过程再故障时，继电保护系统应能准确识别出故障状态，并可靠动作。假设再故障为不对称短路时，可用以下判据作为重新开放保护的条件[4]：

当系统正常运行时，没有负序和零序电流，式(2)不会成立；当系统发生振荡时，由于三相对称，式(2)也不会成立；当系统在振荡过程中发生不对称故障时，总会存在负序电流，甚至是零序电流，式(2)被满足，从而再次开放保护。

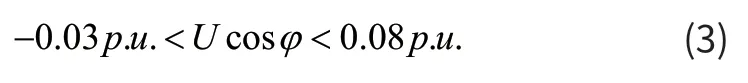
式中，φ为电流落后于电压的相角；p.u.为标幺值。

Ucosφ为电压相量在电流相量方向上的投影，是一个标量。当发生三相短路时，若忽略系统阻抗和输电线路中的电阻，则Ucosφ近似等于故障点处的电弧电压Uarc，其值一般不超过额定电压UN的6%，且与故障距离无关，基本不随时间的变化而变化，式(3)一直满足。在系统发生振荡时，Ucosφ近似等于振荡中心的电压，当φ变化到180°时，该电压值会很小，可能满足式(3)，而当φ变化到其他角度时，该电压值就会很大，式(3)不满足。这便是式(3)所表现出的振荡与三相短路的差异。

■ 3.3 振荡过程再故障的仿真分析

（1）不对称短路的仿真分析

基于振荡过程再故障的解决方案，建立不对称短路的故障判定元件仿真模型，保持系统振荡状态不变，假设线路AB首端（距离母线A处2km）在0.5s发生AB两相短路，m取0.5。仿真波形如图8、图9所示。

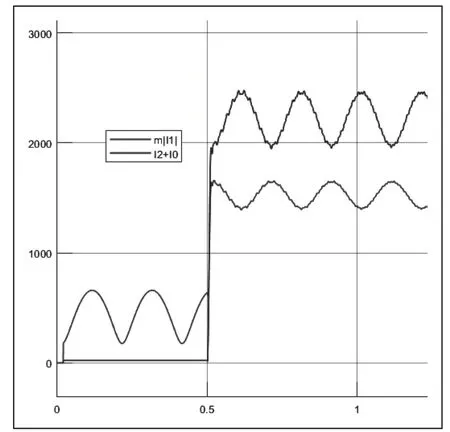
图8 振荡时再发生不对称故障时的仿真结果

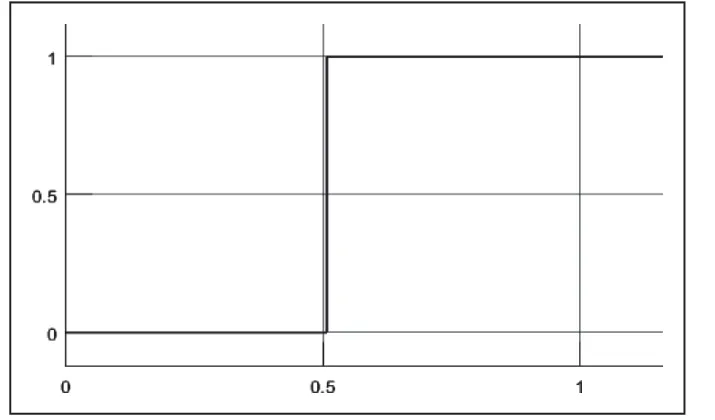
图9 振荡过程中再发生不对称故障时继电器的动作信号波形

由上图可以看到，振荡过程中再发生不对称短路时，只要故障不切除，式(5)就会一直满足，因此继电器动作信号始终为1，保护能够重新开放，及时切除故障。

（2）三相对称短路的仿真分析

在距离保护模型基础上增加三相对称短路的故障判别元件后，假设两侧电动势频率为fM=50Hz，fN=51Hz，当系统发生振荡时，式(3)的仿真结果如图10所示，可以看出，Ucosφ数值变化幅度非常大，式(3)只会在很短的时间内满足，该时间低于0.1s。

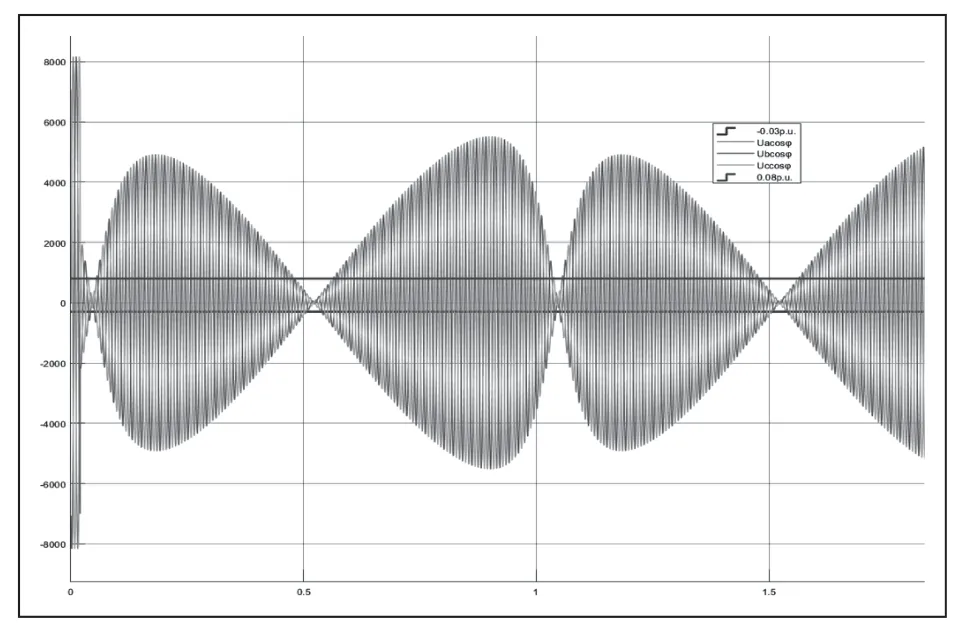
图10 系统振荡时式Ucosφ数值的仿真结果

保持系统振荡状态，在线路AB首端设置三相对称短路，得到Ucosφ数值的仿真结果如图11所示。由图可见：式(3)能够一直被满足，直至故障切除。

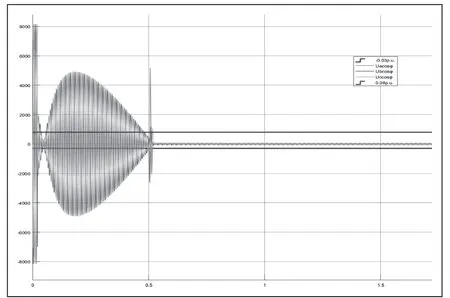
图11 振荡过程中发生三相对称故障时式Ucosφ数值的仿真结果

基于以上分析，将延时模块设置为0.1s。仿真得到继电器的动作信号如图12所示。由图可见：当振荡过程中再发生三相对称故障时，故障发生0.1s后，式(3)还满足，则重新开放保护，保护装置动作，将故障切除。

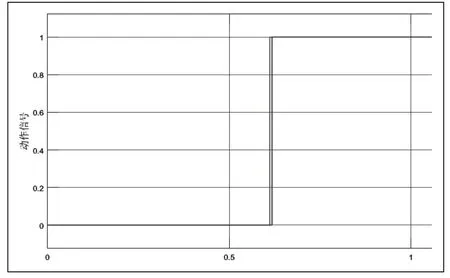
图12 振荡过程中发生三相对称故障时继电器的动作信号波形

4 总结

随着电力系统规模的不断发展，网络结构愈加复杂，发生振荡等不正常运行的情况越来越多，因此，研究振荡过程保护闭锁方案以及再故障的判别方案具有重要意义。本文建立距离保护仿真模型，通过改变电源频率模拟电力系统振荡过程，仿真分析了振荡过程中继电器的动作信号，仿真结果表明：利用阻抗变化率快慢区别系统是故障还是振荡，原理简单，易于实现，且准确可靠；而振荡过程中再发生不对称或者对称短路时，本文采用的判别方案也能够准确识别并开放保护，及时将故障切除，确保距离保护的可靠性。