粤北山区某泥石流风险的精细化评价研究
2022-09-13何宏伟温汉辉何利平
何宏伟,温汉辉,何利平
(广东省有色金属地质局九四〇队,广东·清远 511520)
广东山地面积约占全省土地面积的三分之二,随着城市建设的不断推进,在极端天气、强震和人类活动等多因子耦合作用下,泥石流灾害爆发的频率居高不下。基于此,建立基于动力过程的泥石流风险评估体系,定量识别潜在泥石流风险等级,是山区城市发展规划的迫切需要。
危险性是指灾害发生的可能性、规模和强度。目前泥石流危险性评估以逐渐由经验公式法、物理实验法和统计类比法,发展到以数值模拟为主[1],如:基于FLO-2D对汶川地震后的都江堰龙溪河流域内的12条泥石流沟灾害进行了数值反演分析,综合得出了该地区的泥石流灾害危险图[2];对不同降雨频率下的泥石流进行数值模拟,并表明溃决/非溃决型泥石流的冲出量比值能达2.88倍[3];构建了基于灾害动力过程的风险评估与风险制图方法,进一步提出可用于泥石流减灾防灾风险调控技术[4]。泥石流的易损性是指承灾体可能遭受地质灾害破坏的严重程度,有学者总结了国外对易损性的定义和评估方法,将泥石流灾害的潜在受害者类型分为财产(经济)和人口(生命)两大基本类型,并结合中国西南地区的调查和统计数据,建立了拟合资产、人口和易损性的幂函数方程[5];以舟曲泥石流为背景,揭示了受灾体的破坏特征以及破坏模式,并得出泥石流的密度、深度、速度以及与受损建筑物的结构、材料之间的关系[6];基于非线性回归方法,以泥石流的流深及建筑物高度等参数推导出了阿尔卑斯山脉泥石流堆积区内的建筑物易损性的经验性公式[7];以清平乡泥石流为研究对象,将泥石流堆积区的土地类型划分为建筑、道路、农田并建立了其敏感性因子,在此基础上,以经济损失为主要的评价指标,建立了该冲积扇上泥石流受灾体的易损性分布图[8];针对不同计算模型的不确定性,结合现场调查,构建出泥石流强度与房屋建筑的易损度曲线[9]。
本文通过开展不同降雨频率下的泥石流数值分析,获取泥石流的动力学参数(流速、流深、冲击力等),分别分析泥石流易发区的危险性及受灾体易损性,最后采用泥石流风险评价方法,对泥石流易发区的风险性进行定量化评价,为泥石流防灾减灾提供一定的借鉴意义。
1 研究区概况
研究区位于粤北山区某村后山,其地貌类型属丘陵地貌,地势整体西高东低,相对高差100 m左右。山体整体坡度较缓,下部20°~30°,山顶附近较陡40°~50°,山间多沟谷,坡脚为现状村民房屋,地形起伏大,冲沟发育,地形地貌较为复杂,目前主要已形成两条泥石流支沟N1、N2,总流域面积11810 m2(图1)。
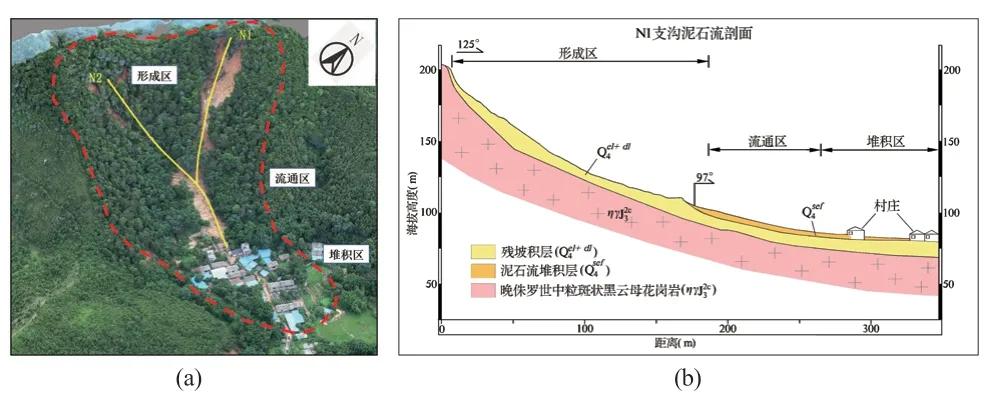
图1 研究区平面(a)与剖面(b)图Fig.1 Plan view (a) and profile section (b) of the study area
2020年6月8日凌晨3时20分,受暴雨影响,该村后山发生泥石流地质灾害(图2)。泥石流裹挟花岗岩块石及树木顺坡面地势低凹处奔流而下,堆积于坡脚村庄内,泥石流一次堆积方量约3000 m3,其规模属于小型。此次泥石流事件冲毁2栋、损毁1栋泥砖房,直接经济损失约80万元,潜在威胁村庄26户157人生命财产安全。

图2 泥石流裹挟的块石(a)与冲垮的房屋(b)Fig.2 Boulders carried (a) and collapsed houses (b) by the debris flow
2 基于动力学模型的泥石流强度分析
2.1 模型构建原理
采用深度积分连续介质力学方法分析上述泥石流运动过程[10]。对x、y、z方向上的质量和动量守恒方程可以表示为:
其中:ρ代表流体的密度;h是流体深度;u和v分别代表流体速度在x和y方向的分量;(τzx)b和(τzy)b分别代表zx和zy方向上的切应力;z是地形标高;kap是侧向土压力系数。
Voellmy模型广泛应用于泥石流数值模拟。基础摩擦应力τ由Voellmy模型计算如下:
其中:μ是摩擦系数,ξ是湍流系数,V是泥石流的平均速度。
公式(1)~(3)由Massflow软件进行求解,其是基于深度积分连续介质力学原理和改进的MacCormack-TVD有限差分方法,该方法在保证计算精度的同时简化了计算过程,极大缩减了计算时间与计算内存需求,所以被广泛运用于地表流灾害数值分析领域。除此之外Massflow采用Fortran语言进行编程,可以进行二次开发。用户可以结合自身研究对象特点对本构模型进行优化,使模型更贴合研究对象[11]。
本文数值模拟的地形数据由无人机倾斜摄影测量获取的高精度地形(分辨率0.05 m),数值模拟网格设置为2 m。泥石流危险评价所用的参数值根据不同重现期的泥石流灾害进行设定。我们使用两个步骤来确定泥石流的参数,第一步参考以往相关研究成果[12-13],基底摩擦系数μ的参考取值范围为0.1~0.3,湍流系数ζ对应的参考取值范围为100~300 m/s2。第二步根据第一步所获取的参数取值范围,利用反演的方法确定具体的计算参数,见表1所示。

表1 数值模拟参数Table 1 Numerical simulation of parameters
2.2 动力学参数设定
泥石流重度采用现场配浆法测定,将浆体准确配置成泥石流运动时的状态,再结合浆体体积计算浆体重度。计算公式如下:

式中:γc是泥石流重度(t/m3);Gc是配置泥石流浆体重量(t);V为泥石流浆体体积(m3)。根据现场配浆结果得到泥石流重度为1.9 t/m3。
采用雨洪法计算泥石流的峰值流量。该方法假定泥石流与降雨同时发生,且具有相同的重现期。泥石流峰值流量(QC)可用以下公式估算。

其中:D是堵塞系数,与沟道的淤积程度有关;φ是泥石流容重的修正系数,定义为:
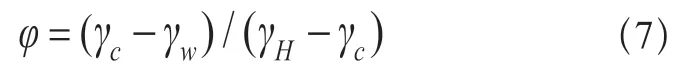
其中:γc为泥石流的密度(kN/m3),γw为水的密度(10 kN/m3),γH为泥石流固体物质密度(26.5 kN/m3)。
洪峰流量(QB)根据《泥石流灾害防治工程勘察规范》(T/GAGHP 006-2018),计算公式如下:

其中:QB(1%)为百年一遇的洪峰流量。F为流域面积(km2),对于研究区,峰值流量(QB)和不同重现期的流量可由以下公式确定:QB(2%)=0.8QB(1%),QB(5%)=0.5QB(1%),QB(5%)=0.3QB(1%)。
3 泥石流灾害的风险评价方法
3.1 危险性评价方法
泥石流对承灾体的破坏能力主要体现在两个方面:淤埋破坏能力以及冲击破坏能力。基于有关评价技术方案[14],提出一套结合最大流体深度以及最大冲击动量的双因素评价模型来定量化评价泥石流的破坏能力(危险性)。这个模型将泥石流强度划分为:极高、高、中、轻度危险区(表2)。

表2 泥石流危险性分区标准Table 2 Criteria for zoning of hazard of the debris flow
3.2 易损性评价方法
易损性指所研究的地质灾害以一定强度发生时对潜在承灾体可能造成的损失程度,常用0-1之间的数字来表征。此外,据相关研究结果[15],表明承灾体易损性可综合采用社会易损性和物质易损性来表示。最后结合研究区的实际情况,采用社会易损性和物质易损性两个指标建立人口和建筑易损性评价体系对泥石流易损性开展研究。
(1)易损性指标选取
由于研究区承灾体结构较简单,本文选取研究区内人口损失(社会易损性)和建筑物的经济价值(物质易损性)作为指标因素进行易损性评价。
(2)易损性评价计算模型
为使两种指标能置于同一数量级上进行比较,需利用公式对其进行转换,结合单沟小流域泥石流易损性的计算公式,研究区泥石流的易损性评价计算模型如下[16]:
式中:V为易损性(0-1);FV1为建筑物的经济价值指标V1(万元)的转换函数(0-1);FV2为人口损失指标V2(人/km2)的转换函数(0-1)

式中:V1为建筑物的经济价值指标;A为建筑物单层的面积(m2);F为建筑物的层数;I为建筑物的造价(元/m2)
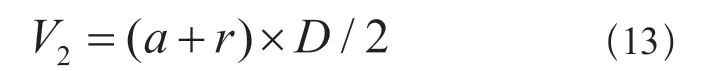
式中:V2为人口损失指标;a为≤13岁的儿童以及≥60岁的老人所占比例(%);r为研究区5年内的人口自然增长率(‰);D为每栋建筑物的人口密度(人/km2)。
(3)易损性指标分析
通过逐户实地调查及参考当地建筑工程造价,研究区建筑物单价取值见表3。

表3 建筑单价取值表Table 3 Values of the construction unit price
利用每栋建筑物的人口数量及年龄结构,计算得到a的值,并结合该地区国家统计数据以及询问当地村民获取的数据,研究区村庄的人口自然增长率取值1.29%。人口密度则通过建筑物的总人口除以建筑物的面积得到。
3.3 风险评价方法
泥石流灾害风险评价是将危险性评价结果与受灾体易损性评价结果进行耦合得到,本文泥石流风险评价方法采用联合国风险计算公式R(风险性)=H(危险性)×V(易损性)将泥石流的危险性及易损性结果进行耦合,计算出不同重现期泥石流风险度值,再通过分区标准将村庄的承灾体划分为不同风险区,具体明确地展示出风险水平。
参考有关研究[17-19],首先将危险区分区图低、中、高、极高危险性分别赋值为1、2、3、4,同时将易损性分区图低、中、高、极高易损性分别赋值为1、2、3、4;再运用ArcGIS栅格计算器将危险性和易损性图层进行赋值计算得到泥石流威胁区域内不同承灾体的风险度值,最后通过风险计算公式计算风险度,计算标准见图3,当R>9时,属于极高风险;当4<R 9,属于高风险;当2<R 4,属于中风险;当R<2,属于低风险。
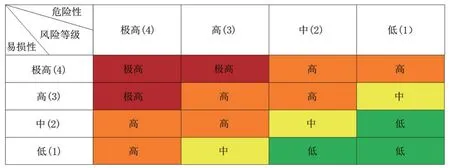
图3 泥石流定量风险评价标准Fig.3 Criteria for quantitative risk assessment of the debris flow
4 结果分析
4.1 模型验证
村庄后山属于典型的沟道型泥石流,根据现场调查访问、泥石流监测及视频资料分析,将启动点设置在1#断面(启动点1)处和2#断面(启动点2)处,在启动点处设值流量过程线。为简单起见,将流量过程线简化为概化五边形模型进行计算,根据现场调查访问将流量过程线持续时间T设置为300 s,泥石流最终堆积图如图4所示。
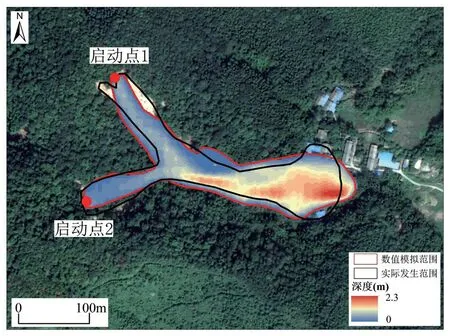
图4 泥石流反演结果对比Fig.4 Comparison between results of back analyses of the debris flow
为验证数值结果的准确性和合理性,结合相关研究成果[20],使用Ω开展数值模型的验证分析,Ω表示模拟结果和实际发生的泥石流堆积体的重叠程度,Ω=2表示完美的重叠,Ω= -2表示没有重叠,其中Ω的定义如下:
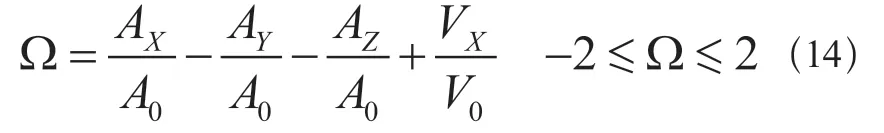
式中:AX表示正确判断面积,AY表示错误判断面积,AZ表示缺失判断面积,VX正确判断的区域,A0表示现场调查面积,V0表示现场调查体积。
经计算Ω=1.44,精度为72%,表明此次泥石流数值计算结果与现场调查结果较为一致,证明该套数值模拟参数和模型能较好应用于泥石流灾害数值计算。
4.2 泥石流危险性评价结果
采用已验证的计算参数和数值模型开展不同重现期泥石流灾害数值模拟。数值模拟结果表明:不同重现期泥石流均对村庄造成严重威胁,其主要区别在于泥石流运动过程中运动速度v、运动深度h及堆积区面积和堆积深度不同(图5)。其中10年一遇最大堆积深度1.8 m,20年一遇泥石流堆积区堆积深度一般介于0.1~2 m,最大堆积深度2 m,主要威胁约6栋房屋;50年一遇泥石流堆积区堆积深度一般介于0.1~2.3 m,最大堆积深度2.3 m,主要威胁约19栋房屋;100年一遇泥石流堆积区堆积深度一般介于0.1~2.7 m,主要威胁约26栋房屋。根据数值模拟的结果,在不同重现期下大量泥石流主要沿沟道淤积,相对来说,村庄北部区域则处于相对安全位置。

图5 不同重现期泥石流堆积深度图Fig.5 Depth of debris flow accumulation with different recurrence intervals
各重现期泥石流的最大速度云图如图6所示,从图中可以看出10年一遇、20年一遇、50年一遇、100年一遇,最大速度分别为5.5 m/s、5.7 m/s、6.0 m/s、6.7 m/s,随着降雨量的增大,泥石流最大速度逐渐增大,且最大速度出现在泥石流中部位置。

图6 不同重现期泥石流速度云图Fig.6 Cloud map of debris flow velocity with different recurrence intervals
基于3.1节泥石流最大流深h和最大冲击动量hv的双因素分区标准,并使用ArcGIS软件中栅格处理工具将泥石流危险性划分为极高、高、中和低四种危险区,见图7。
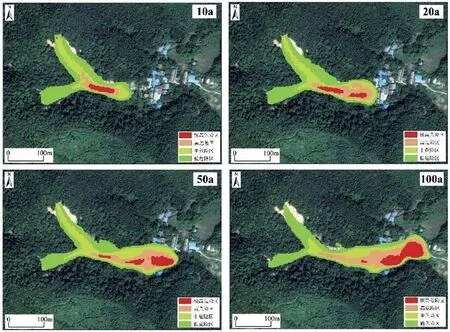
图7 不同重现期泥石流危险性分区图Fig.7 Zoning of debris flow hazards with different recurrence intervals
根据数值计算结果流深和动量综合考虑泥石流淤埋破坏和冲击破坏能力,定量评价不同重现期泥石流危险性,见表4所示。模拟结果表明:10年一遇危险性相对较小,20年一遇、50年一遇、100年一遇的泥石流灾害均会对村庄建筑物、道路和农田造成较为严重的危害,其中20年一遇极高危险区和高危险区面积分别为1300 m2和3384 m2,中危险区和低危险区面积分别为5640 m2和10872 m2;50年一遇极高危险区和高危险区面积分别为2164 m2和4272 m2,中危险区和低危险区面积分别为9120 m2和9856 m2;100年一遇极高危险区和高危险区面积分别为3816 m2和6028 m2,中危险区和低危险区面积分别为6196 m2和10680 m2。
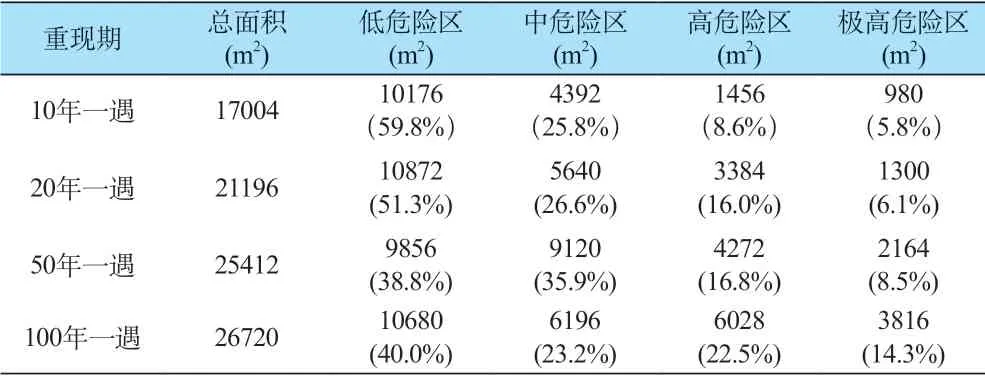
表4 不同重现期泥石流危险区统计表Table 4 Statistics of debris flow caution areas with different recurrence intervals
4.3 易损性评价结果
易损性评价结果计算主要有三步:首先根据现场调查的建筑物、人口等数据分别代入公式(12)和(13)得出建筑物的经济价值指标V1和人口损失指标V2的值;再将V1和V2分别代入公式(10)和(11),得出建筑易损性指标的函数转换值FV1和人口易损性指标的函数转换值FV2,计算结果见表5。从表中可以看出人口易损性相比建筑易损性的数值较低,建筑易损性主要集中在0.4~0.6,人口易损性主要集中在0.1~0.3。

表5 易损性指标分布表Table 5 Distribution of vulnerability indicators
根据现场调查访问,村庄人口分布结果分布见图8a,建筑结构结果分布见图8b;最后将FV1和FV2带入公式(9)中,得到研究区承灾体易损性综合评价结果8c,通过GIS统计可知,极高易损性建筑面积为721 m2,高易损性建筑面积为3156 m2,中易损性建筑面积为1133 m2,低易损性建筑面积为221 m2。从结果可以看出易损性与建筑物结构类型及人口数量密切相关,结构越差,人口越多则易损性越高。
4.4 风险评价结果
通过上述泥石流风险评价方法对研究区风险性进行划分,得到了不同重现期泥石流定量风险评价结果,见表6及图9所示,具体明确地展示了不同承灾体的风险水平。模拟结果表明:10年一遇泥石流风险区面积17004 m2,其中高风险区占比5.0%,中风险区占比9.3%,低风险区占比85.7%,主要威胁农田;20年一遇泥石流风险区面积21401 m2,其中极高风险区占比0.6%,分布建筑物1栋,高风险区占比7.1%,分布建筑物2栋,中风险区占比16.0%,分布建筑物2栋,低风险区占比76.3%,分布建筑1栋;50年一遇泥石流风险区面积为26112 m2,其中极高风险区占比4.1%,分布建筑物6栋,高风险区占比11.5%,分布建筑物7栋,中风险区占比14.1%,分布建筑物3栋,低风险区占比70.3%,分布建筑物3栋;100年一遇泥石流风险区面积为27754 m2,其中极高风险区占比5.6 %,分布建筑物9栋,高风险区占比18.1%,分布建筑物10栋,中风险区占比18.7%,分布建筑物5栋,低风险区占比57.6%,分布建筑物2栋。随着降雨频率的增加,受威胁的房屋逐渐增加,因此,建议完善沟内拦挡治理措施及加强泥石流监测预警工作。

表6 不同重现期泥石流风险区统计Table 6 Statistics of debris flow risk areas with different recurrence intervals

图9 不同重现期泥石流风险分区图Fig.9 Risk of the debris flow with different recurrence intervals
5 结论
本文以深度积分连续介质力学方法作为泥石流动力学过程的定量化获取手段,建立耦合泥石流淤埋深度和冲击动量的泥石流强度评价指标,考虑人口和建筑易损性构建泥石流风险评价体系,主要得出以下结论:
(1)基于N-S方程构建泥石流运动演进物理模型,使用该动力学模型对此次泥石流反演结果与现场调查结果较为一致,在此基础上对不同重现期(10年一遇、20年一遇、50年一遇和100年一遇)泥石流灾害进行数值计算。结果表明:随着降雨强度的增加,危险面积由17004 m2增加至26720 m2,其中百年一遇极高危险区、高危险区、中危险区和低危险区面积分别占比14.3%、22.5%、23.2%和40.0%。
(2)根据统计的建筑物和人口数据,研究区一层砌体结构建筑物占92%,每栋建筑物的人口数量在3~6人左右,以幼老年人为主。易损性主要受建筑物结构类型及人口数量影响,由综合考虑建筑物结构类型和人口的易损性评价模型得极高易损性房屋5栋,高易损性房屋15栋,中易损性房屋4栋,低易损性房屋2栋。
(3)根据风险评价的结果,10年一遇泥石流主要威胁对象为农田;而20年一遇、50年一遇、100年一遇泥石流则会对建筑物造成威胁,其中20年一遇泥石流位于极高风险区建筑物1栋,高风险区建筑物2栋,中风险区建筑物2栋,低风险区建筑物1栋;50年一遇泥石流位于极高风险区建筑物6栋,高风险区建筑物7栋,中风险区建筑物3栋,低风险区建筑物3栋;100年一遇泥石流位于极高风险区建筑物9栋,高风险区建筑物10栋,中风险区建筑物5栋,低风险区建筑物2栋。建议完善沟内拦挡治理措施及加强泥石流监测预警工作。
