小区开放对交通影响的微元建模及评价*
2022-09-13张为苗张其斌
张为苗,张其斌△,王 娜,李 婷,封 蕾
(1.甘肃省计算中心,甘肃 兰州 730030;2.甘肃省云计算重点实验室,甘肃 兰州 730030)
随着城市的发展,城市人口和车辆的增加,道路交通阻塞问题日益显著。对此,国务院发布《关于进一步加强城市规划建设管理工作的若干个意见》,其中第十六条关于推广街区制,原则上不再建设封闭住宅小区,已建成的住宅小区和单位大院要逐步开放等意见,引起了广泛关注和讨论。在此背景下,针对小区开放前后周边交通情况,探讨小区开放后对周边道路通行的影响具有重要的意义。
受周围环境的影响,通行力与小区周边诸多因素有关,不能一概而论。小区开放后,一方面小区周边可用来通行的道路面积增加,可有效缓解道路交通阻塞问题;另一方面道路面积的增加可能导致岔路的增多,交叉路口的车辆也会增多,反而加剧交通阻塞。
本研究针对小区开放前后周边交通的情况,探讨了小区开放后对周边道路通行的影响。用模糊数学法建立了一个关于交通拥挤度的模糊数学推理评价指标体系,根据交通拥挤度[1]的取值判断小区开放之后对小区周围道路的影响;基于微元法的思想建立了车辆通行的数学模型,并用该模型定量分析三种典型类型的小区开放对周边道路通行的影响。
1 模型假设
1)假设不考虑小区的地理位置。
2)假设MSFi=507pcu/h。
3)假设车辆在小区附近的输入量等于输出量。
4)假设某小区及附近路段的服务水平在某特定时刻内是相同的。
5)假设驾驶员对车辆行驶速度的影响忽略不计。
6)假设小区内部的小路不允许机动车辆经过。
2 符号说明
本文通过数学模型建立、数据分析、实证举例等方式来研究小区开放对交通的影响。在该过程中将部分概念抽象为数学符号以便于模型的建立和实际问题数学化、公式化的表述。符号及符号含义说明见表1。

表1 符号说明
3 评价指标体系的建立
3.1 建模前的准备
相关名词解释及术语如下:
1)基本通行能力。忽略道路的外在环境包括道路的交通控制、天气情况等影响因素,在一段道路或特殊的横截面上,车道在规定的时间间隔内(一般为15 min),所允许通过的标准车辆的最大小时流率。
2)理想条件。路面状况干净整洁没有障碍物,气候条件适宜驾驶,驾驶员熟悉道路环境。
3.2 模型建立
引入交通拥挤度的概念,交通拥挤度与交通流基本参数有关。由交通拥挤度的评估方法,可选取行驶速度、行车密度、实际车流量与最大交通量的比值,运用模糊数学的方法分析交通流基本现象与交通拥挤现象之间的关系,建立起一个关于交通拥挤度的模糊数学推理评价指标体系。
交通拥挤度的评价方法如下[2]:
科学家Morris.Rothenberg将交通拥挤定义为“一般情况下,在道路服务水平可承受的范围之内,车道上的交通量超过道路所能负荷的最大交通量就是交通拥挤”。当比值小于0.77的时候,道路交通处于饱和状态,大于0.77道路开始发生拥挤现象。将衡量交通是否拥挤的评价指标体系定义为交通拥挤度c,且为0~1的实数。参数c越小,交通越流畅,c越接近于1,那么也就认为交通越拥挤。
选取小区附近机动车辆的行驶速度、行车密度、实际车流量与最大交通量的比值3个交通指标来评价小区开放前后道路通行的拥挤度。将拥挤度与所选取的交通指标建立函数关系:

式中,M代表小区开放前后实际道路通行的拥挤度,λ1,λ2,λ3代表分别对应的权重值,Mv,Mk,Mq分别代表行车速度、行车密度、实际车流量与最大交通量的比值所对应的函数关系。
行车速度v与拥挤度的函数关系函数为Mv:
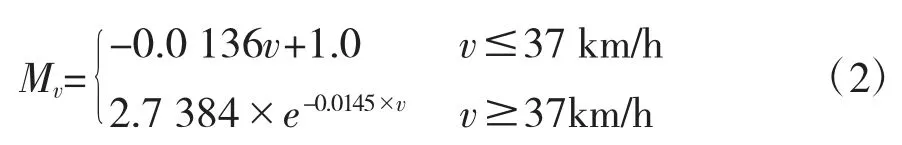
行车密度k与拥挤度的函数关系函数为Mk:
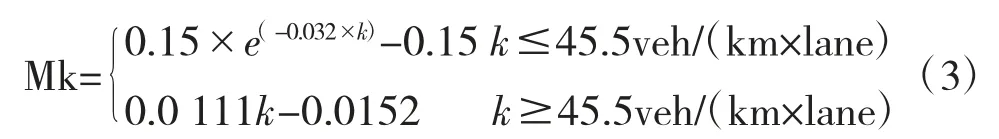
实际车流量与最大交通量的比值q与拥挤度的函数关系函数为Mq:

3.3 结论
因为0≤Mq,Mk,Mv≤1,所以0≤c≤1,根据c的取值可以很好的反映小区开放之后的交通拥挤度,即对小区周围道路交通的影响,见图1。
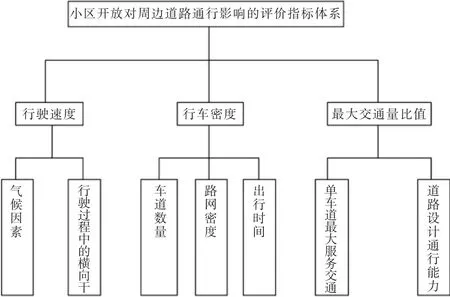
图1 影响交通拥挤度的体系示意图
4 建立车辆通行的数学模型
4.1 模型建立
将车辆的特性、驾驶人员特性、单向车道数等因素抽象化、数学化、模型化[3],得到某特定时段特定地点即该公路截面瞬时的实际通行能力。由于得到的实际通行能力只是某公路段截面瞬时实际通行能力,并不能代表某一区域或路段的连续实际通行能力。若将该连续实际通行能力看作要求的函数,则截面瞬时实际通行能力可看作该函数的一个微元[4-6](一个极小部分,因为其具有可加性、有序性、平权性,所以可以将它看做一个微元)。基于上述分析,可利用微元法将截面瞬时实际通行能力在给定路段长度内积分,得到一个路段的连续实际通行能力。即可得出小区开放对周边道路的通行是有益还是无益。
在该实际问题中,某路段截面的道路实际通行能力:
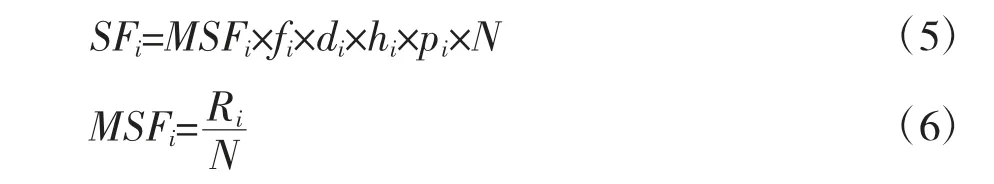
其他参数都为已知常数,所以可将截面实际通行能力简化为SFi=ωRi。,其中ω代表常数。
1)若将某路段的道路实际通行能力看作整体U,将U相应的分成n个部分量△Um,则由SFi的定义可知:

2)部分量SFi可近似表示成SFi(Ri)△Ri,且SFi与SFi(Ri)△Ri之差是△Ri的高阶无穷小,即:
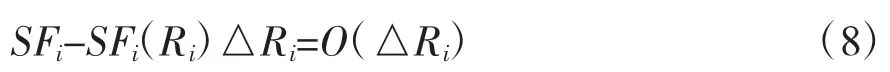
那么,可得所求某一路段道路实际通行能力U的数学模型为:

由于各小区及附近区域的道路条数不同及道路上级别不同,根据现实经验,道路有主干道,次干道等多级干道之分,不同等级的道路对应的各个影响因素的参数也就不为相同。为方便研究分析,建立更一般化的模型,我们将小区周边的各条道路进行标号,用i表示(假设开放小区前附近的道路条数为n1,开放后可通行道路条数为n2)。j代表影响每条道路通行能力参数所对应的等级。
则可建立某路段或区域实际道路通行更一般化模型:

由于开放前后只有道路条数在变,所以得到小区开放前后实际通行能力比:

已知,SFi=MSFi×fi×di×hi×pi×N,
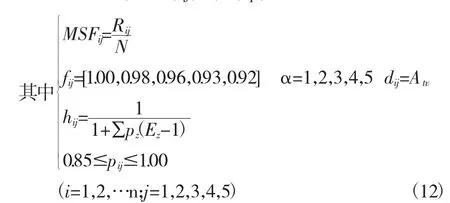
所以用各条道路在某截面瞬时通行能力积分和的平均值表示小区周边所有道路的连续实际通行能力。
道路通行能力是某级服务水平对应的单车道MSFi、fi、di、hi、pi、N这六个元素的乘积,其中:
1)MSFi为是给定等级服务水平对应下的单车道最大交通服务量,Ri为某等级服务水平下车道的总服务量与多车道公路单向车道数之比。具体含义是指服务水平为给定等级的第i条道路中,对应单车道的最大服务交通量。
2)fi分级,见表2。
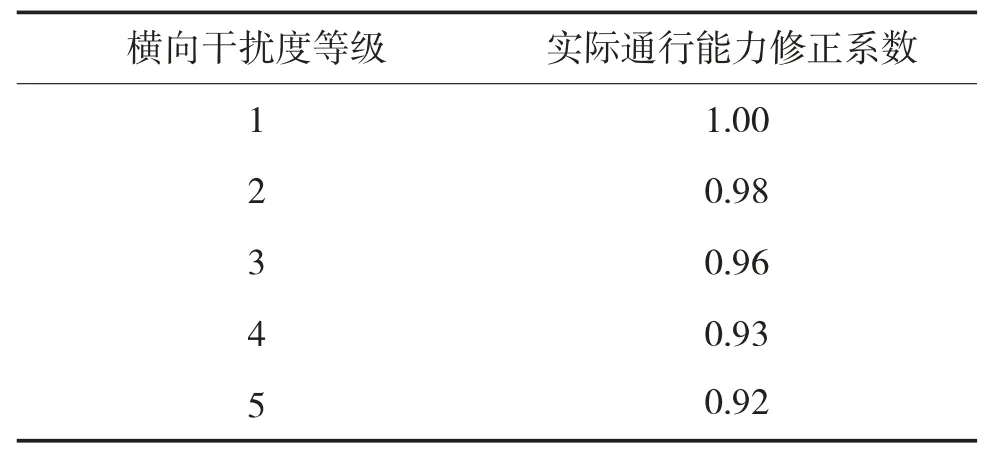
表2 横向干扰影响的修正系数
fi即表示为第i条道路。
3)本研究中用di表示平交路口的密度修正系数,同样考虑到该系数在三个不同层次速度情况下的取值不同,将三个不同速度情况看做是三个不同的速度等级,具体相关关系表3。
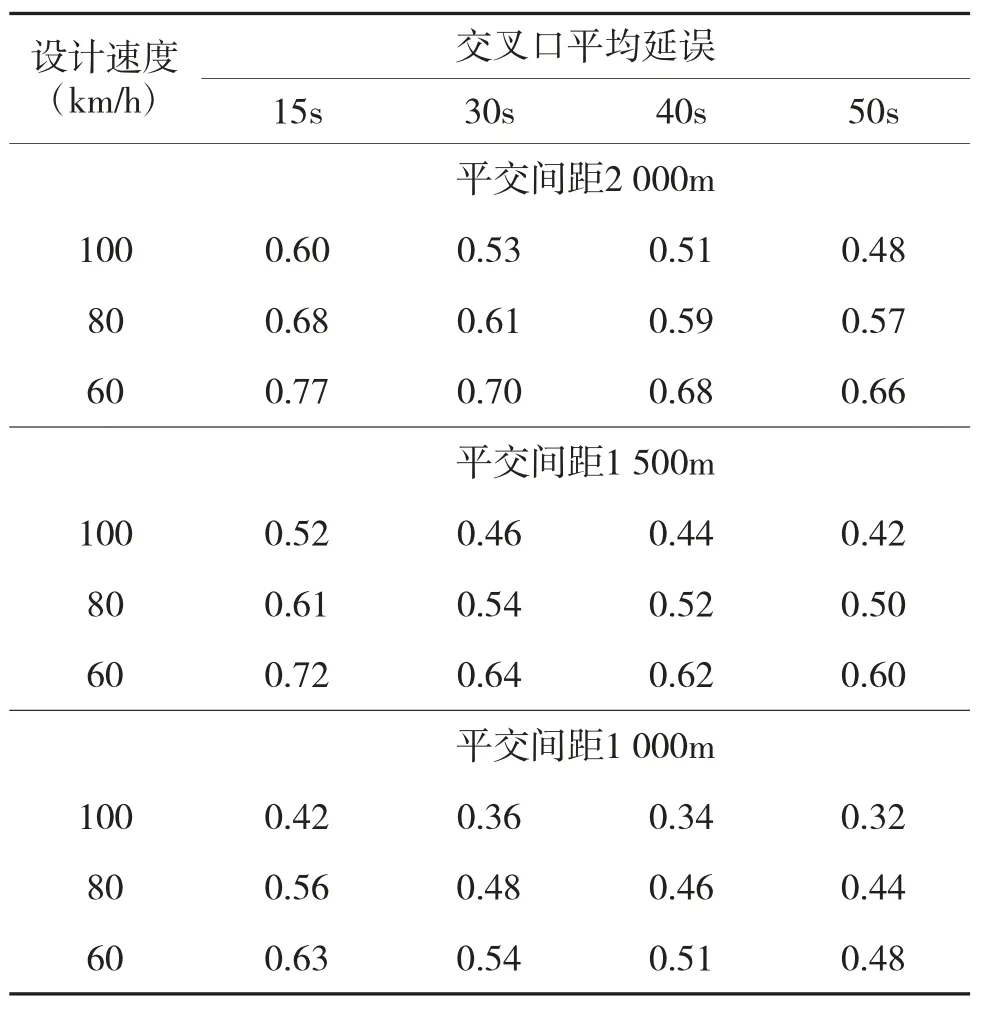
表3 平交路口密度的修正系数
在该条件中,路口的平交间距分别为2 000 m,1 500 m,1000m时交叉口的平均延误时间t分别取15s、30 s、40 s、50 s,车辆通行的速度为ν,分别取100 km/h、80 km/h、60 km/h,则可得到di的取值矩阵Atv,该矩阵的取值分别如下:
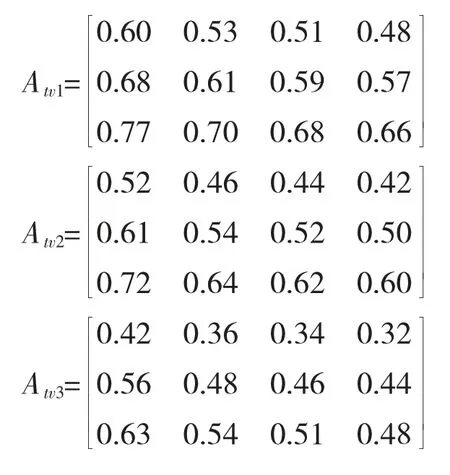
4)hi表达式为车型z的分类说明及各车型的车辆折算系数分别见表4,表5。

表4 多车道公路车型分类
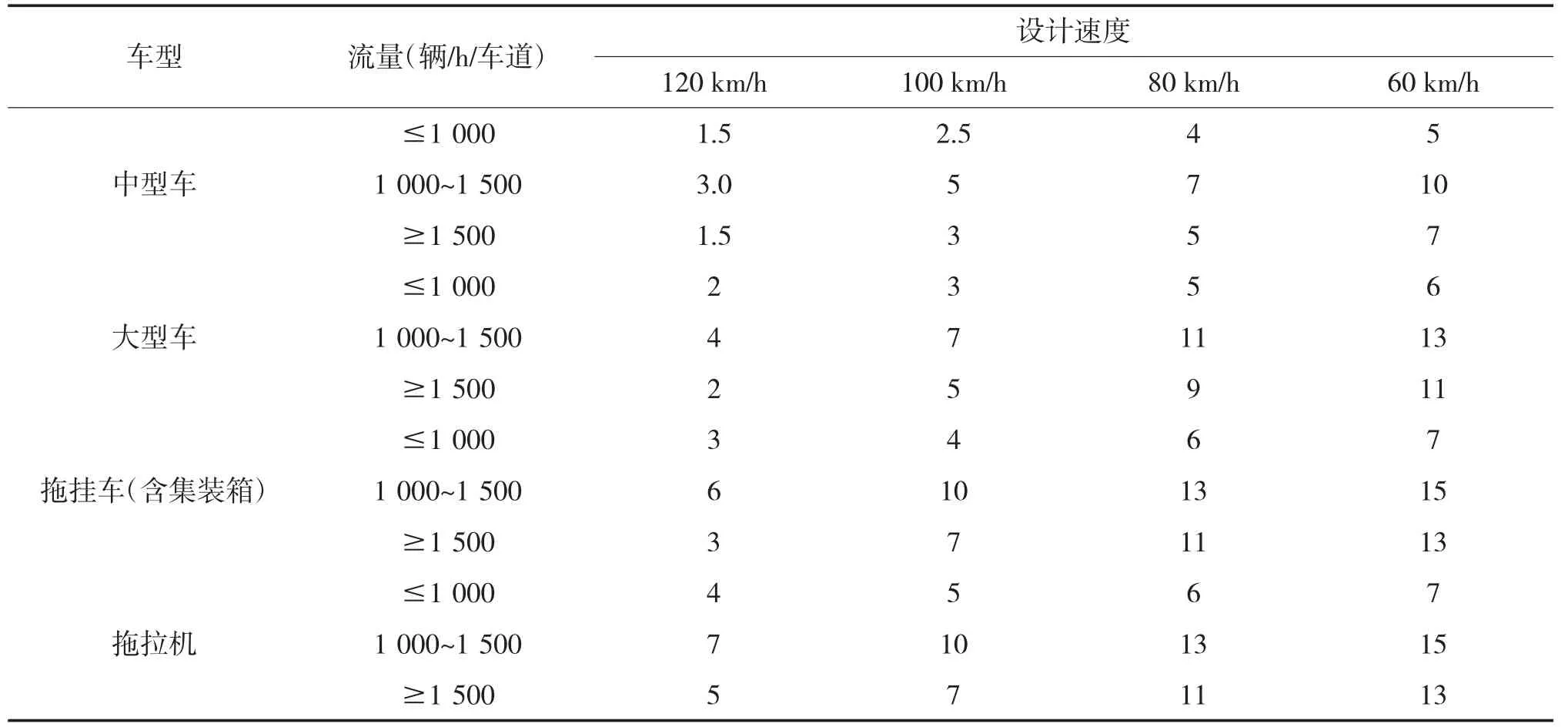
表5 多车道公路车辆折算系数的推荐值
5)多车道公路驾驶中驾驶员总体特征的影响是通过pij来反映的.其取值范围在0.85~1.00。
基于上述分析和条件,可以将小区开放前后所有车道的连续实际通行能力进行比值分析,从而得到小区开放前后连续实际通行能力比的数学模型为:

4.2 分析三种典型类型的小区
根据收集到的小区类型和资料,筛选出三种典型类型的A,B,C[7-8]小区进行比较分析。
(1)田型公路附近小区开放前后对其通行的影响。根据国家标准对小区道路建设的相关要求,该小区的数据分析见表6。
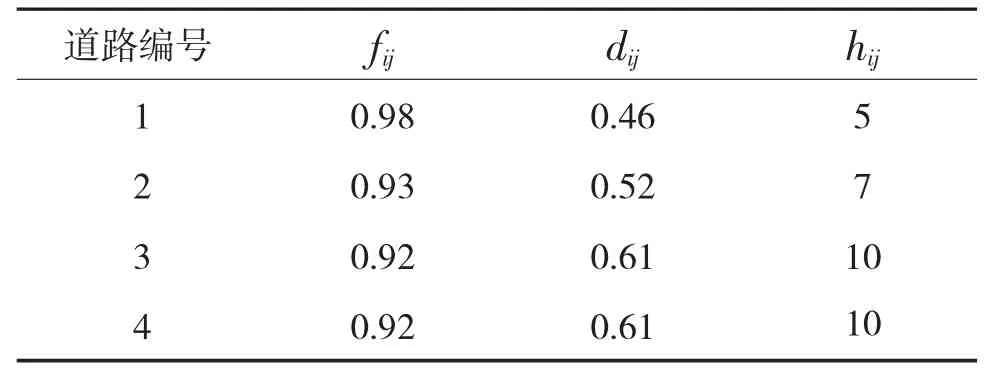
表6 A小区周边道路系数
小区开放前后的示意图见图2,图3。
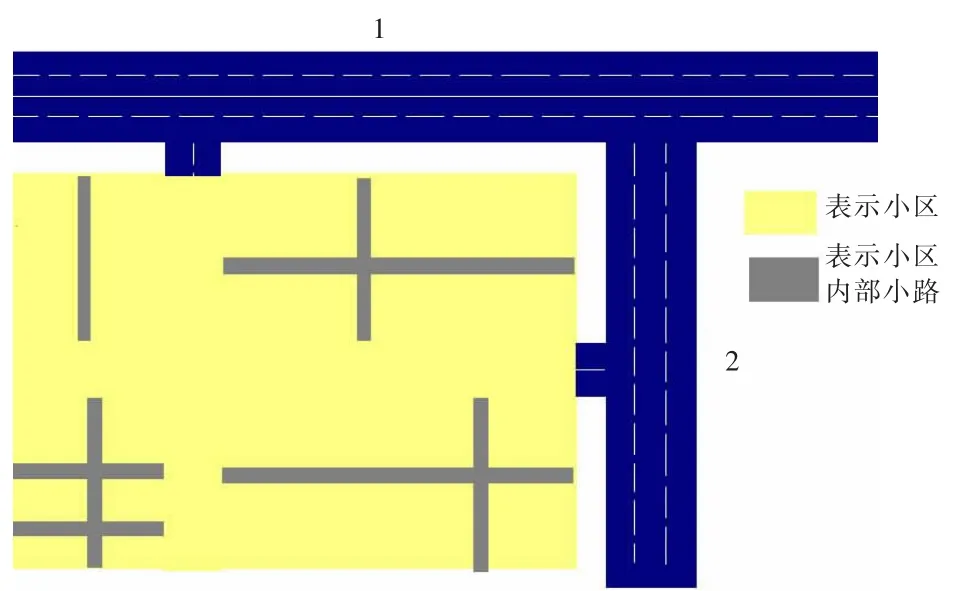
图2 A小区道路开放前
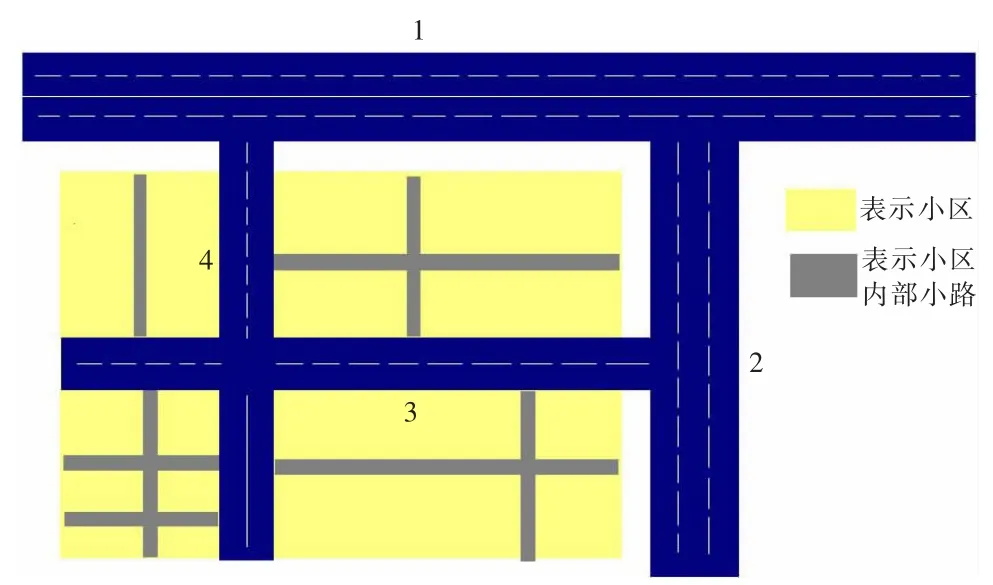
图3 A小区道路开放后
根据评价指标体系的模型,现已知道路单向条数N,假设j级服务水平对应下的单车道最大交通服务量MSFi=507pcu/ h[9-11],将fi,di,hi带入评价指标体系的模型,然后利用Matlab编程计算得到:
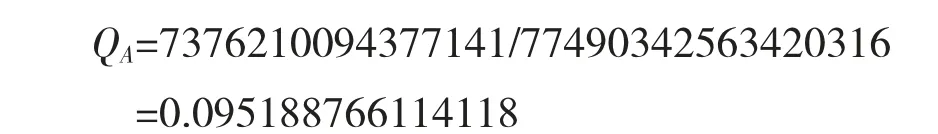
(2)U型公路附近B小区开放前后对其通行的影响,见表7。
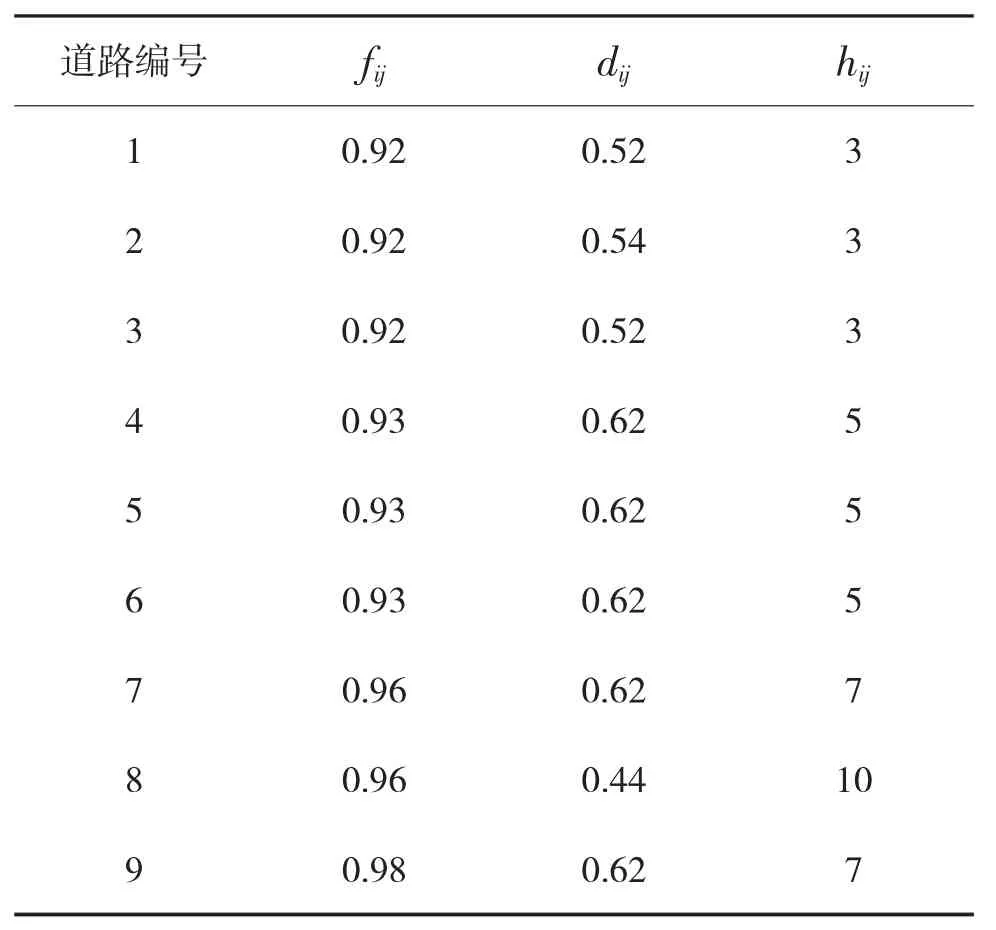
表7 B小区周边道路系数
B小区开放前后的示意图见图4,图5。
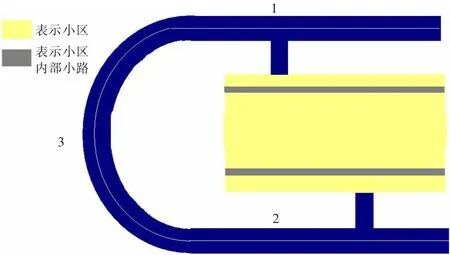
图4 B小区道路开放前
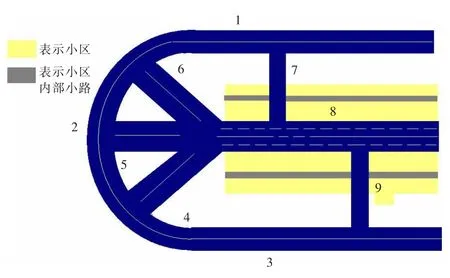
图5 B小区道路开放后
同A小区的计算过程,将数据带入,得到结果为:

(3)环型公路附近C小区开放前后对其通行的影响。
C小区数据见表8。
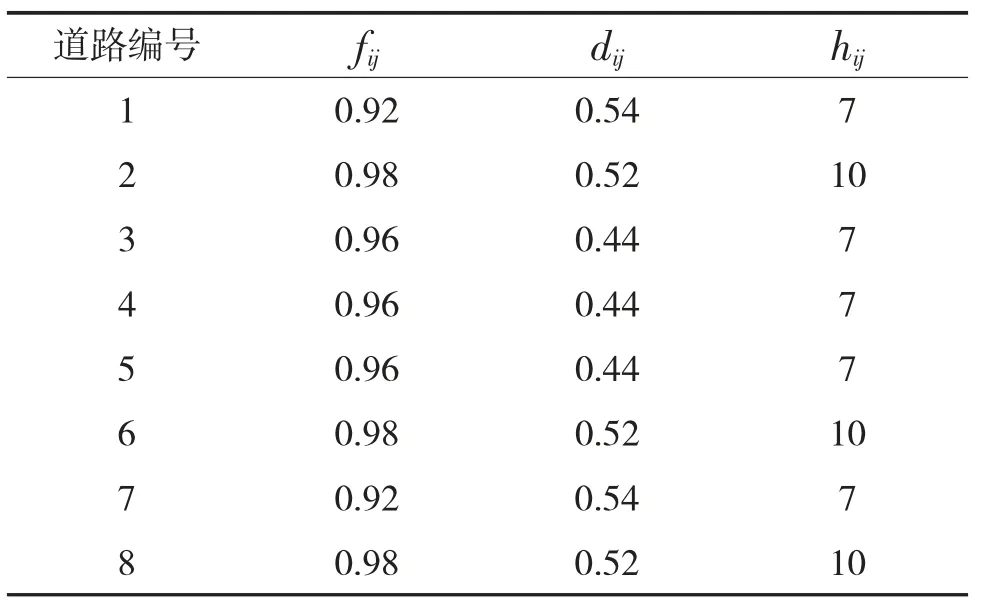
表8 C小区周边道路系数
该小区开放前后示意图见图6,图7。
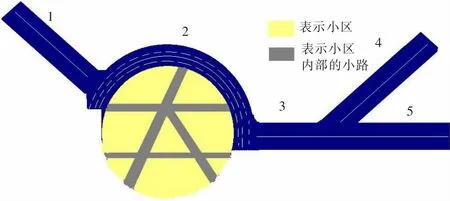
图6 C小区道路开放前
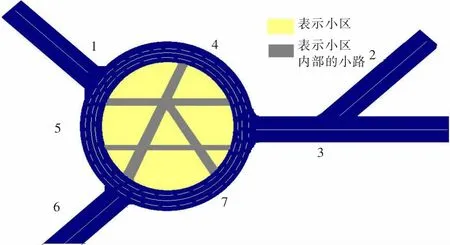
图7 C小区道路开放后
同A,B小区的计算方式,计算可得

4.3 小结
比较A,B,C三小区的小区开放前后实际通行能力比QA,QB,QC可得:QA>QC>QB,即田型公路附近小区开放后对其周边地区通行的影响最差,U型公路附近小区开放后对其周边地区通行的影响最好。
5 结论
本研究针对小区开放前后周边交通的情况,根据交通拥挤度的取值判断小区开放之后对小区周围道路的影响;建立了车辆通行的数学模型,并用该模型定量分析了三种典型类型的小区开放对周边道路通行的影响。得到以下结论:
1)因为0≤Mq,Mk,Mv≤1所以0≤C≤1,根据C的取值可以很好地反映小区开放之后的交通拥挤度,即对小区周围道路交通的影响。
2)比较A,B,C三小区的小区开放前后实际通行能力比QA,QB,QC可得:QA>QC>QB,即田型公路附近小区开放后对其周边地区通行的影响最差,U型公路附近小区开放后对其周边地区通行的影响最好。
6 向交通管理部门提出关于小区开放的合理化建议
根据得出的模型来看,小区周围路段的交通拥挤度由周围车辆的行驶速度、行车密度、实际车流量与最大流量的比值等因素决定[12-14],而这些影响因素也与时间段,如周一到周五的早高峰和晚高峰,即有的小区开放后对附近地区道路通行有有益影响,而有的小区开放后对周围地区的道路通行并无有益影响。所以建议,从目前来看,可在一些大城市内在早晚高峰时段开通一些处于重要路网节点上的小区以缓解交通压力。
要依据小区附近的路网结构来规划是否开放小区以及开放到什么样的程度,由评价指标体系的模型及车辆通行模型求出的结果来看,小区附近的路网越密集,则开放小区对道路通行能力的影响不大;若小区附近的路网越稀疏,则开放小区后对道路通行拥挤情况会起到缓解作用。所以建议开放或半开放稀路网且位于城市核心区的小区。
