肢腿履带足机构抬腿工况动力学分析与实验研究

赵富强，杜 特，常宝玉，牛志刚

（1.太原科技大学重型机械教育部工程研究中心，山西 太原 030024；2.太原理工大学极地工程与装备研究院，山西 太原 030024）

为满足肢腿履带足机构的工作要求，避免其在运行过程中因肢腿部件强度不够而导致结构变形，有必要对其抬腿工况的动力学特性展开研究，以提高其在极端负载条件下的安全稳定性。

目前，对于肢腿履带足机构的研究主要集中在肢腿受力分析方面。苏学满等［1］对一种柔性腿式机器人越障时的动力学问题进行了研究，求得了其柔性腿动作时所需的驱动力矩。程乾等［2］采用拉格朗日法求解得到了电液驱动六足机器人单腿机构各关节在运动过程中的驱动力矩。边兵兵［3］对机械臂进行了刚柔耦合动力学联合仿真，得到了其在不同工况下的受力规律，并预测了其运动规律和应力分布。江维等［4］对带电作业机器人的机械臂进行了动力学建模，推导得到了机械臂的动力学方程，并通过动力学仿真验证了所构建动力学模型的正确性以及机械臂各关节的动态性能。申浩宇等［5］利用解耦的自然正交补方法消除了多自由度串联机器人动力学方程中的约束力，得到了一种高效的反向动力学递推建模方法，并通过编制程序对七自由度串联机器人进行仿真，验证了所提出方法的可靠性和高效性。宁会峰等［6］采用拉格朗日法建立了光伏组件清扫机械臂的动力学方程，并得到了机械臂各关节所受的广义力和力矩，同时通过动力学仿真结果和实验结果的对比为机械臂驱动系统的选择和驱动函数的改进提供了依据。Xie等［7］基于模块化并联机构的运动理论、拉格朗日方程等建立了单驱动六足机器人的动力学模型，研究了其曲柄轴转角与驱动力矩的关系，并通过ADAMS（automatic dynamic analysis of mechanical systems，机械系统动力学自动分析）动力学仿真验证了所构建动力学模型的合理性。Sorin等［8］为实现对六足机器人腿部结构的控制，结合正运动学模型和逆运动学模型，构建了基于拉格朗日法的腿部结构动力学模型，并开展了相应的腿部控制实验。Ding等［9］采用拉格朗日法建立了NOROS-Ⅱ车轮运动时的动力学模型，得到了其在3种不同路径下的俯仰力矩，并利用ADAMS动力学仿真验证了所建立动力学模型的有效性。Staicu［10］利用第二类拉格朗日法求解了某类轮腿式机器人的动力学参数，得到了其驱动轮的扭矩，这为解决其运动控制问题提供了参考。黄鸣辉等［11］运用ADAMS软件和ANSYS软件对作业状态下的挖掘机动臂和斗杆进行了结构强度的瞬态分析，所得结果可为挖掘机工作装置的结构设计提供参考。任志贵等［12］利用基于动平衡方程计算的动载荷谱对液压挖掘机进行了应力瞬态分析，得到了其整体工作装置的动力学特性。邢伟等［13］对巨型机械臂进行了动力学仿真以及动态应力测试，并通过联合仿真验证了该机械臂的可靠性，进一步为大型复杂设备的研发提供了依据。程靖等［14］基于拉格朗日方程建立了闭链双臂空间机器人的动力学模型，结合约束条件获得了其动力学方程，并设计了该机器人的自适应控制方案，完成了对其载荷位置和姿态运动的精确控制。仇鑫等［15］推导并验证了六自由度机器人的正、逆运动学方程，并对其实物样机重要部件的强度进行了校核，同时通过计算得到了实物样机可承受的最大静态载荷，为机器人的动力学控制奠定了基础。刘广军等［16］建立了反铲液压挖掘机的刚-柔耦合动力学模型，并以其各油缸的位移曲线为驱动，通过仿真得到了其动臂和斗杆上各点的应力，并与实际应力测试结果进行对比，验证了仿真结果的正确性。冯豪等［17］提出了整体动态模型与局部子模型相结合的方法，并对挖掘机工作装置进行了瞬态动力学分析，得到了精确的局部应力，并通过理论计算结果与和实验测试结果的对比验证了所提出方法的正确性。

综上所述，笔者拟利用理论推导、动力学仿真和实验相结合的方法对肢腿履带足机构单腿抬起工况进行动力学分析，以验证其结构的安全性与合理性。

1 肢腿履带足机构抬腿工况动力学建模

1.1 肢腿履带足机构结构及其单腿抬起工况

肢腿履带足机构的整体结构如图1所示，主要由上、下面板形状均为正六边形的支撑平台和均布在其各端角位置上的6个肢腿系统（编号为a～f）构成，其可完成复杂的抬腿、越壑和避障等功能。单肢腿系统包括上回转装置、上肢腿、下肢腿、一级电动推杆、二级电动推杆、下回转装置和履带足。其中：上回转装置可实现肢腿在水平方向上的转动；上肢腿在竖直方向上的转动由布置在两侧的一级电动推杆驱动；下肢腿在竖直方向上的转动由1个二级电动推杆驱动，其与下回转装置通过十字轴承连接，以实现履带足的仰俯与侧倾；下回转装置上环形均布着4个压簧（在肢腿抬起过程中可减少履带足晃动）；履带足是实现整个机构平稳行驶的牵引结构。

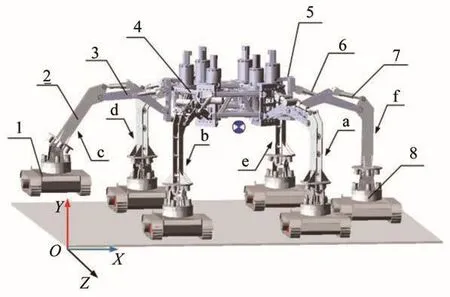
图1 肢腿履带足机构整体结构Fig.1 Overall structure of limb-leg crawler foot mechanism

当肢腿履带足机构抬腿工作时，其抬起腿的结构强度受扭矩的影响最大，故对其抬腿工况的动力学特性进行分析。如图1所示，当肢腿履带足机构位于水平地面且单腿（肢腿c）抬起时，肢腿c的一、二级电动推杆从初始位置收缩到极限位置，使其履带足抬至最高状态，其余5条肢腿均处于支撑状态，此时整个机构的质心位置在x方向上的变化情况如图2所示（质心初始位置为-62.125 mm处）。分析肢腿c在抬起过程中的位姿变化情况，结果如图3所示。其中，1为初始位姿，2为终止位姿。由图可知，在肢腿c抬起过程中，整个肢腿履带足机构的质心会发生偏移：从初始状态开始，电动推杆加速启动导致整个机构的质心沿x正向最大偏移0.14 mm；随着电动推杆的收缩，抬起腿出现晃动，从而导致整个机构的质心偏移；当一、二级电动推杆收缩至极限位置时，整个机构趋于稳定，其质心回到初始位置。

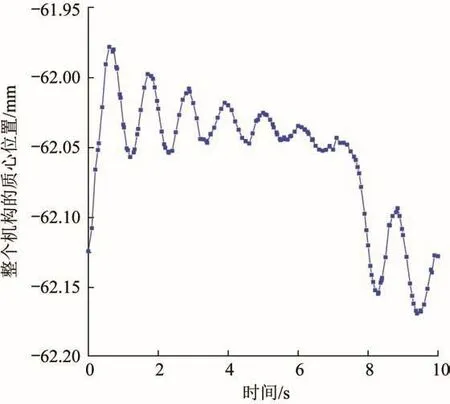
图2 单腿抬起工况下肢腿履带足机构的质心位置（x方向）Fig.2 Centroid position of limb-leg crawler foot mechanism under single leg lifting condition(x direction)

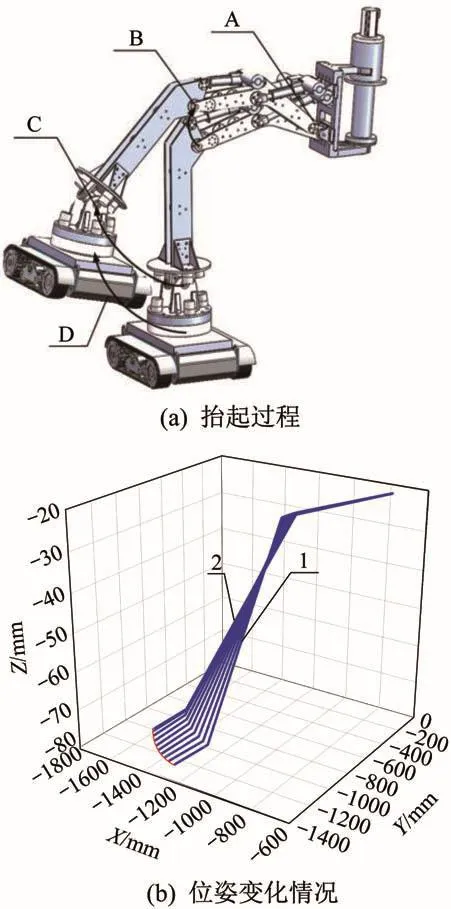
图3 肢腿c的抬起过程及其位姿变化情况Fig.3 Lifting process of leg c and its position and posture changes

1.2 单肢腿系统动力学建模与分析

为了研究在肢腿履带足机构单腿抬起工况下其抬起腿（忽略下回转装置弹簧力作用）关节的受力情况，以便于后续的强度分析，以单肢腿系统为研究对象，采用拉格朗日法［18-19］建立其抬起工况的动力学模型，从而求解其关节的驱动力矩。如图4所示，以上肢腿与上回转装置的铰接点I为原点构建直角坐标系。图中：θ1为上肢腿与水平方向的夹角，θ2为下肢腿与水平方向的夹角；lB为上肢腿的长度；lC为上、下肢腿铰接点M到下肢腿与履带足铰接点Q的距离；l3为履带足质心与铰接点Q的竖直距离。

由图4可得，在单肢腿系统抬起的过程中，其上肢腿的动能TB为：

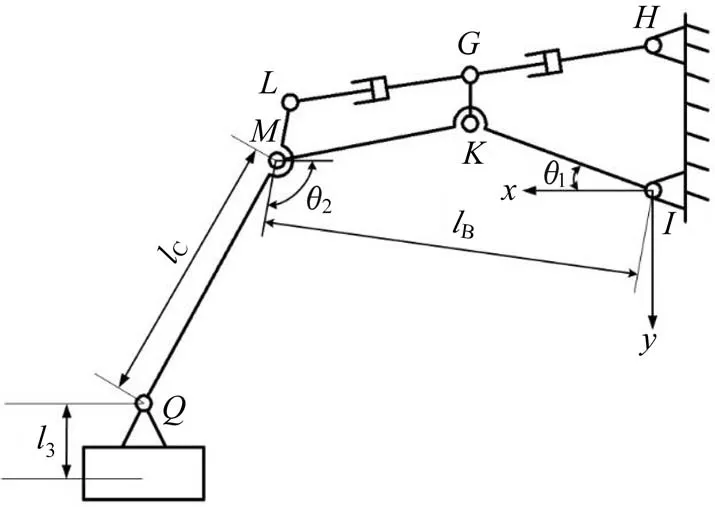
图4 单肢腿系统抬起工况动力学模型Fig.4 Dynamics model of single limb-leg system under lifting condition

式中：mB为上肢腿的质量；l1为上肢腿质心与坐标系原点的距离。

上肢腿的势能VB为：

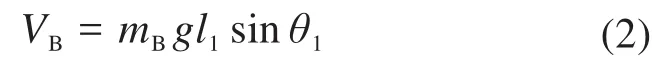
式中：g为重力加速度。

下肢腿的动能TC为：

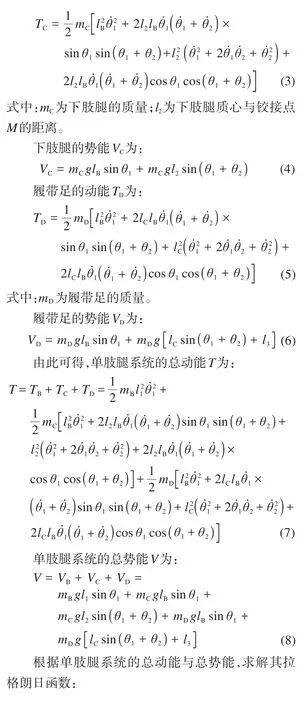
为验证所构建的基于拉格朗日法的单肢腿系统抬起工况动力学模型的正确性，利用ADAMS软件对单肢腿系统抬起工况进行动力学仿真。在开始仿真前，在单肢腿系统的铰接点I、M处分别添加角度驱动，其对应的函数分别为 step（time，0，0，10，0.234 5）和step（time，0，0，10，0.375 9）。提取抬腿周期内单肢腿系统铰接点I、M在不同时刻的角度、角速度和角加速度等运动参数，并将其输入MATLAB软件以求解这2处的驱动力矩。基于ADAMS动力学仿真和MATLAB求解获得的单肢腿系统铰接点I、M处的驱动力矩如表1所示。对比表1中数据可知，在单肢腿系统抬起2 s时，铰接点I、M处驱动力矩的相对偏差较小；随着θ1、θ2的增大，铰接点I、M处驱动力矩的相对偏差增大，但2种求解方式所得结果的变化趋势一致，由此验证了所构建动力学模型的正确性。

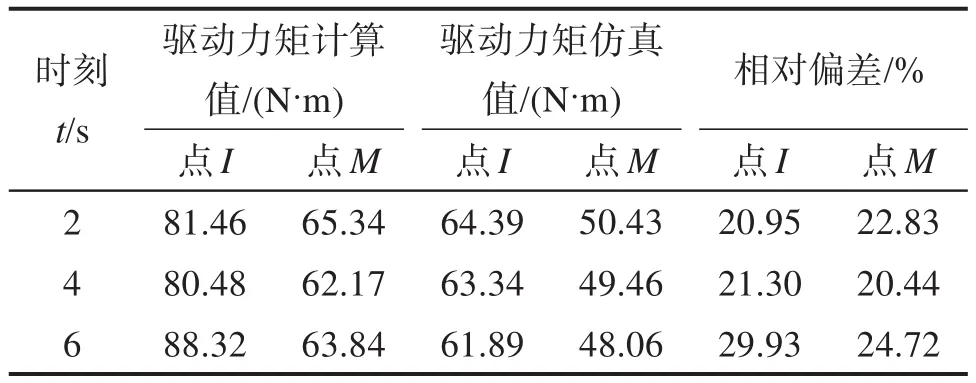
表1 单肢腿系统铰接点I、M处的驱动力矩对比Table 1 Comparison of driving torque at the hinge points I and M of single limb-leg system

2 肢腿履带足机构抬腿工况动力学仿真

为模拟复杂地形下肢腿履带足机构单腿抬起时的受力情况，从而为其肢腿系统的强度校核提供动载荷数据，采用ADAMS软件进行动力学仿真［20］。构建的肢腿履带足机构单腿（肢腿c）抬起工况动力学仿真模型如图5所示。

图5 肢腿履带足机构单腿抬起工况动力学仿真模型Fig.5 Dynamics simulation model of single leg lifting condition of limb-leg crawler foot mechanism

仿真前，在肢腿c的一、二级电动推杆处添加移动副，其余铰接点处添加转动副。根据电动推杆的初始位置，测得肢腿c的一、二级电动推杆分别收缩53 mm和50 mm后可达到极限位置，故按速度方式设置其驱动函数，如表2所示。肢腿履带足机构单腿抬起工况动力学仿真模型的约束参数如表3所示。

表2 肢腿c电动推杆的驱动函数Table 2 Driving function of electric push rod of leg c

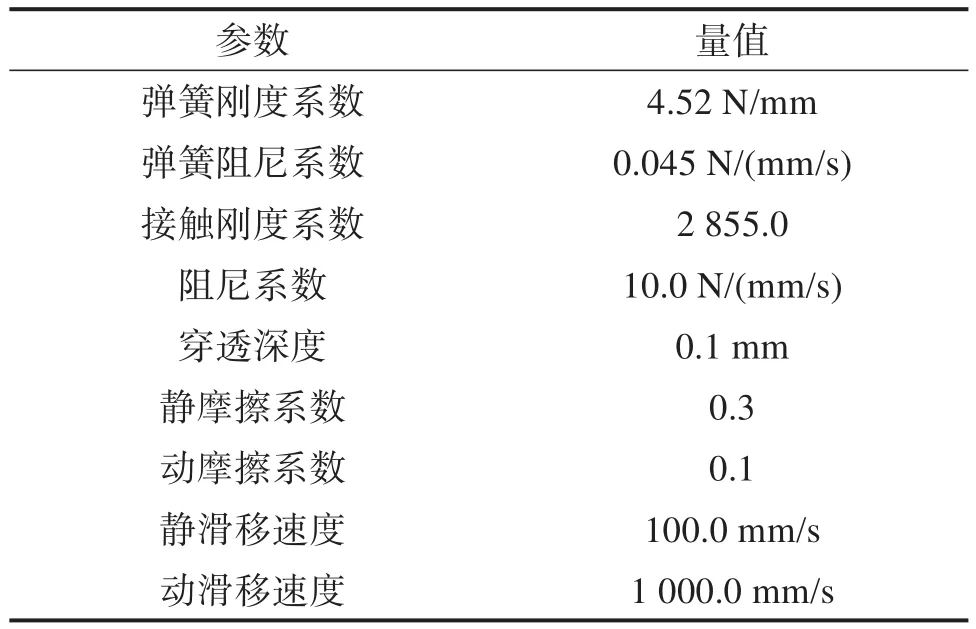
表3 肢腿履带足机构单腿抬起工况动力学仿真模型约束参数Table 3 Constraint parameters of dynamics simulation model of single leg lifting condition of limb-leg crawler foot mechanism

通过提取动力学仿真数据得到肢腿c履带足质心的加速度和其余肢腿（支撑腿）铰接点Q处受力（可反映履带足支撑力的变化趋势）随时间的变化曲线，分别如图6和图7所示。

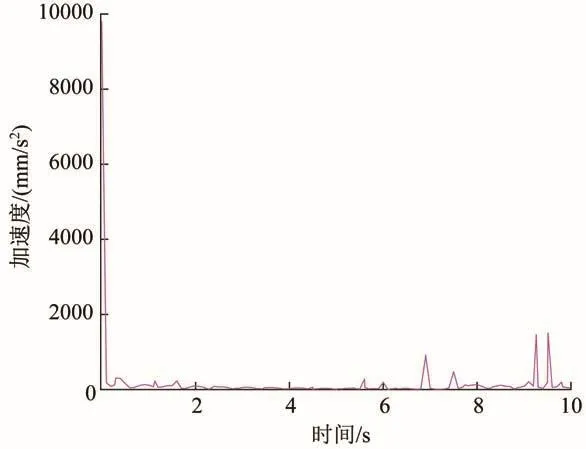
图6 肢腿c履带足质心加速度随时间的变化曲线Fig.6 Variation curve of acceleration of leg c crawler foot centroid with time

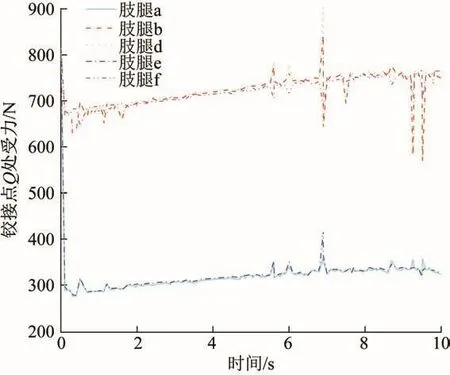
图7 各支撑腿铰接点Q处受力随时间的变化曲线Fig.7 Variation curve of force at hinge point Q of each support leg with time

由图6和图7可知，在肢腿c抬起过程中，其履带足质心处的加速度在不同时刻会发生突变，对应时刻下各支撑腿铰接点Q处的受力也会变化；在肢腿c从开始抬起至0.20 s阶段，由于其电动推杆处于启动阶段，整个肢腿履带足机构的质心在重力作用下瞬间下移且该阶段的速度增量过小，造成其履带足的加速度急剧下降，从而导致肢腿b、d的铰接点Q处受力的下降幅度比肢腿a、e小；在肢腿c抬起的0.22—0.72 s阶段，由于其电动推杆的速度达到最大以及下回转装置的弹簧逐渐被压缩，使得肢腿a、b、d、e的铰接点Q处受力均呈先下降再上升的趋势；在肢腿c抬起的1.10—8.80 s阶段，各支撑腿铰接点Q处的受力出现突变是由肢腿c履带足的运动惯性以及整条肢腿的势能所产生的冲击载荷而导致的；在肢腿c抬起的9.20—9.60 s阶段，其电动推杆的速度均已减小至0 mm/s，下回转装置弹簧的压缩程度以及其运动惯性均已达到最大，这些因素共同导致该阶段各支撑腿铰接点Q处的受力突变。在整个抬腿过程中，由于肢腿f与肢腿b、d共同支撑整个肢腿履带足机构，故其铰接点Q处受力的变化趋势与肢腿b、d的相反或相同且幅度较小。由图7还可知，在肢腿c抬起的整个过程中，肢腿b、d的铰接点Q处受力最大，平均合力为726 N，这是因为肢腿b、d关于肢腿c对称且距离肢腿c最近，在肢腿c抬起过程中，肢腿履带足机构的质心偏向肢腿b、d；同理，肢腿a、e也关于肢腿c对称但其距离肢腿c较远，故其铰接点Q处的受力最小，平均合力为318 N；肢腿f、c位于肢腿履带足机构的横向对称中心线上，其与肢腿b、d分别构成三角支撑状态，以确保在肢腿c抬起过程中整个肢腿履带足机构不会侧翻，其铰接点Q处的受力较肢腿b、d的小，平均合力为718 N。

以肢腿c和受力最大的肢腿d为对象，分析其各铰接点处受力的变化曲线，结果分别如图8和图9所示。

由图8和图9可知，在一、二级电动推杆收缩至极限位置的过程中，肢腿c除铰接点Q处只受重力外，其他铰接点处的受力均与时间呈正比，而肢腿d各铰接点处的受力较平稳；这2条肢腿各铰接点处的受力均在不同时间段出现突变。其中：在5.47—6.10 s阶段，电动推杆收缩使得肢腿c出现振动，因振动产生的冲击载荷造成肢腿铰接点处的受力出现2次突变；在6.80—7.00 s阶段，肢腿铰接点处受力出现突变是因为肢腿c履带足在抬升过程中通过十字轴承向下滑转。当肢腿c抬至最高位置后，其重力全部作用在铰接点H、I处，鉴于一级电动推杆和上肢腿均为二力杆件，故铰接点I、K为肢腿c的受力支撑点；同理，其余5条肢腿承受了整个肢腿履带足机构的重力，其电动推杆处于锁止状态，因此支撑平台的重力作用在其铰接点I处。肢腿c的铰接点I、K处受力的变化趋势大致相同且最大，整体大于肢腿d铰接点I处的受力，该结果与理论分析结果一致。因此，须对抬起腿（肢腿c）进行强度校核，以验证其上、下肢腿在动载荷作用下的安全性与稳定性。

图8 肢腿c各铰接点处的受力情况Fig.8 Force at each hinge point of leg c

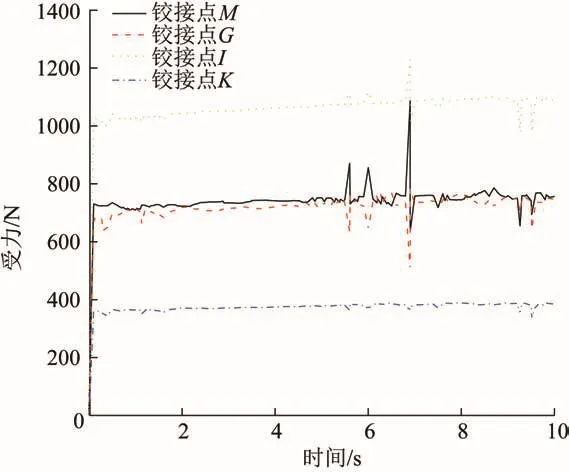
图9 肢腿d各铰接点处的受力情况Fig.9 Force at each hinge point of leg d

3 肢腿履带足机构抬起腿强度校核

3.1 强度有限元模拟

当肢腿履带足机构肢腿c抬至最高位置时，其上肢腿同时受到上回转装置和一级电动推杆的作用力，下肢腿受到二级电动推杆作用力和履带足重力。故在利用有限元软件ABAQUS对肢腿c的强度进行模拟时，将通过动力学仿真得到的动载荷作为边界载荷施加到肢腿上：上肢腿的铰接点G、K完全固定，对铰接点I、M施加动载荷；下肢腿铰接点M完全固定，对铰接点L、Q施加动载荷。鉴于ADAMS软件和ABAQUS软件中坐标系方向不同，对由动力学仿真获得的铰接点I、M、L、Q处x、y、z向的受力Fx、Fy、Fz按式（13）进行转换。

式中：F'x、F'y、F'z分别为有限元模拟中肢腿c各铰接点处x、y、z向的受力。

在ABAQUS软件中分别对肢腿c的上、下肢腿的铰接点I、M、L、Q设置x、y、z向的单位力，并结合式（13）将由ADAMS动力学仿真所得的动载荷数据导入ABAQUS软件，进而实现动态力的加载。通过有限元模拟可得，在抬起工况下肢腿c的上、下肢腿在动载荷作用下的最大应力、最大应变云图分别如图10和图11所示。

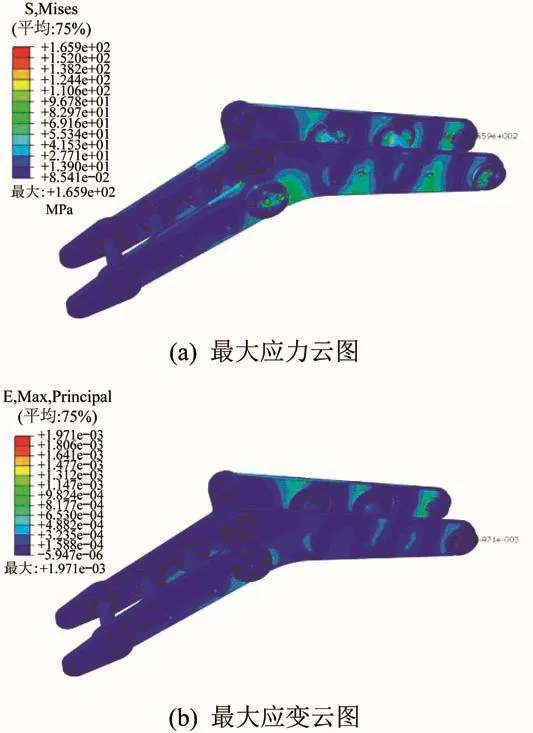
图10 抬起工况下肢腿c上肢腿的最大应力和最大应变云图Fig.10 Nephogram of maximum stress and maximum strain of upper limb of leg c under lifing condition

由图10可知，在抬起工况下，肢腿c上肢腿的最大应力为165.9 MPa，危险截面出现在与受力杆组连接的左侧侧板的最右端限位槽边缘处，该侧板材料为7075铝合金，其屈服极限是505 MPa，则整个上肢腿结构的安全系数为3.04；最大应变出现在右侧侧板的最右端限位槽边缘处。由图11可知，下肢腿的最大应力为122.9 MPa，危险截面出现在上、下肢腿铰接点右侧的受力杆组的中心内孔边缘处，下肢腿的材料为Q345E，其屈服极限是345 MPa，则整个下肢腿结构的安全系数为2.81；最大应变出现在其与上肢腿铰接点附近的右侧侧板限位槽内孔边缘处。综上可知，抬起腿上、下肢腿的强度均满足动载荷作用下的要求。

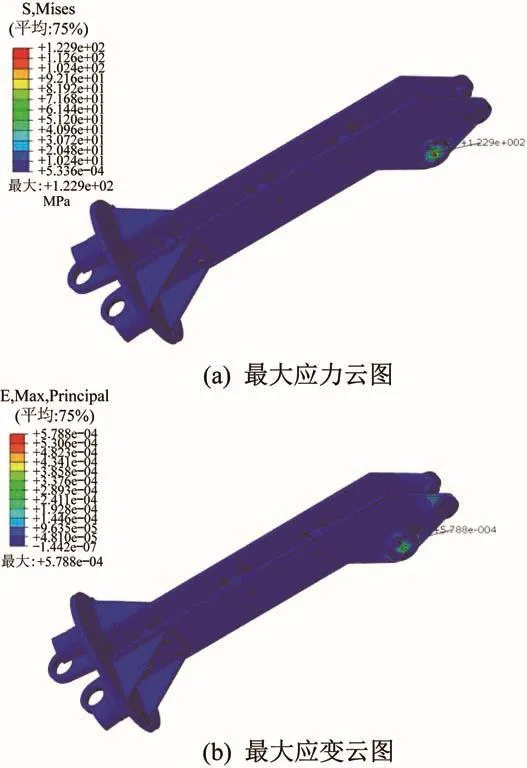
图11 抬起工况下肢腿c下肢腿的最大应力和最大应变云图Fig.11 Nephogram of maximum stress and maximum strain of lower limb of leg c under lifing condition

3.2 应力测试

为测试肢腿履带足机构肢腿系统的抗破坏及抗变形能力，对抬起工况下单肢腿系统的上、下肢腿开展应力测试，以验证有限元模拟结果的正确性。根据有限元模拟结果，在上、下肢腿侧分别选取5个测点（包含最大应力位置）以及在铰接点附近选取10个测点，以开展应力测试实验。在实验前，单肢腿系统的初始状态为一、二级电动推杆部分伸出，使得上肢腿水平、下肢腿与地面垂直；开始实验时，电动推杆在0.20 s内加速到0.5 mm/s后保持匀速，最终在0.20 s内减速收缩至极限位置。通过采样频率为1 000 Hz的JZZ 2019-2557多通道采集仪及型号为BE120-3AA-P500、电阻为（120.6±0.1）Ω、灵敏系数为2.22±0.01的应变片（见图12）共同采集应力数据。

图12 单肢腿系统应力测试现场Fig.12 Stress test site of single limb-leg system

抬起工况下单肢腿系统上、下肢腿的应力测试曲线如图13所示，其中，正值表示受拉，负值表示受压。对比上、下肢腿铰接点处最大应力的模拟值和测试值，结果如表4所示。

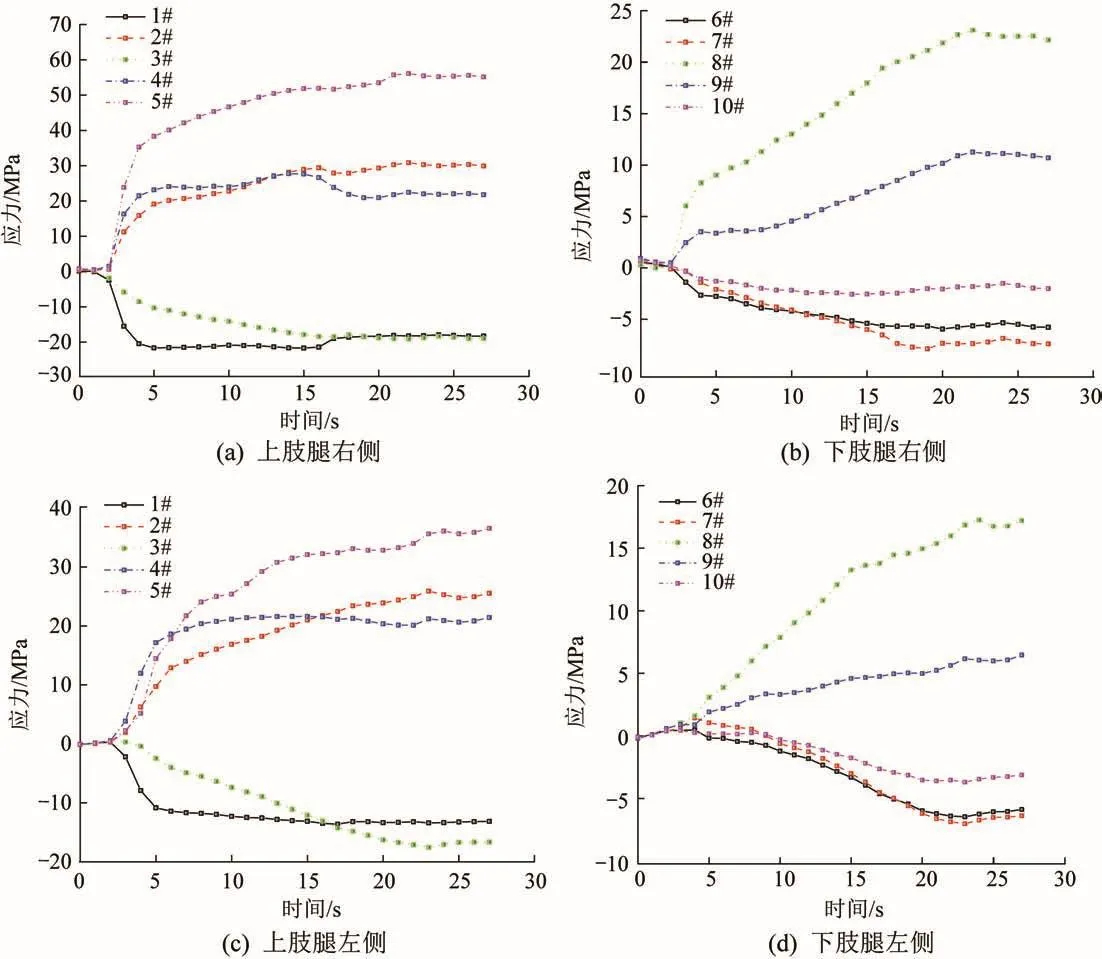
图13 抬起工况下单肢腿系统的应力测试曲线Fig.13 Stress test curve of single limb-leg system under lifting condition

由图12、表4可知，单肢腿系统左、右两侧对称测点的应力变化趋势基本一致且铰接点附近测点的最大应力与模拟结果的相对误差均在18%以内。模拟值与测试值存在误差的原因有：1）电动推杆实际测试速度与仿真的驱动设置存在误差；2）应变片与有限元模型所对应的节点位置不完全一致；3）有限元模型的简化、边界条件的处理方式及数据采集仪的测量误差等。

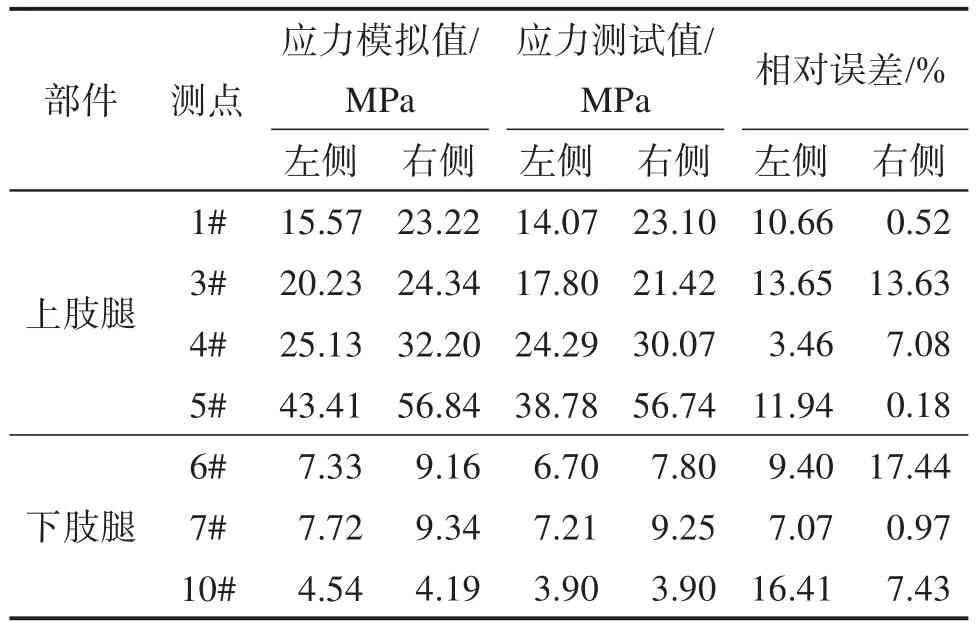
表4 抬起工况下单肢腿系统各测点处最大应力比较Table 4 Comparison of maximum stress at each measuring point of single limb-leg system under lifting condition

4 结 论

针对肢腿履带足机构在单腿抬起工况下的运动特性，建立其单肢腿系统抬起工况的动力学方程，并对肢腿履带足机构进行抬腿工况动力学仿真，分析其抬起腿和支撑腿的受力趋势，得到了受力最大的抬起腿的各铰接点受力情况，并对抬起腿上、下肢腿进行了强度有限元模拟和应力测试，所得结论如下：

1）基于拉格朗日法对单肢腿系统抬起工况进行动力学建模，推导了其上、下肢腿关节驱动力矩的表达式。通过抬腿工况动力学仿真发现，当抬起腿的一、二级电动推杆收缩至极限位置时，受力最大的支撑腿为最靠近抬起腿两侧的肢腿，且抬起腿各铰接点处的整体受力比受力最大的支撑腿还要大；与抬起腿位于横向对称中心线上的支撑腿与受力最大的2条支撑腿所构成的三角支撑状态可使整个肢腿履带足机构在单腿抬起过程中始终保持稳定，结果验证了整个机构在抬腿工况下的稳定性。

2）通过对所受载荷最大的抬起腿的强度进行有限元模拟可得，其上肢腿的最大应力为165.9 MPa，安全系数为3.04；下肢腿的最大应力为122.9 MPa，安全系数为2.81，均满足单腿抬起过程中的强度要求；抬起腿各铰接点处最大应力的模拟值与测试值的最大相对误差均在18%以内，验证了有限元模拟结果的正确性。