基于ISM和GAHP的武器系统选型评价方法
2022-09-09郝坤鹏杨国来张磊葛建立
郝坤鹏, 杨国来, 张磊, 葛建立
(1.南京理工大学 机械工程学院, 江苏 南京 210094; 2.西安昆仑工业(集团)有限责任公司, 陕西 西安 710043)
武器装备研制是一项庞大、复杂的系统工程,涉及诸多学科领域,包含有分系统和设备,其系统结构、指标体系层次复杂,综合评估难度大。同时,在武器装备论证初期,许多指标可能还处于定性描述阶段,量化程度低,这就给多方案择优带来较大困难。为提高方案择优的精准性,有必要应用系统工程理论和方法,对武器系统组成要素之间的关系进行分析,构造系统树状结构图,寻找底层基础要素,对暂时无法量化的指标,利用专家系统,按指标重要性和方案先进性,依据经验进行定量评价,最终确定武器装备综合性能定量评价值,从而找出最优方案,给武器系统论证、选型提供依据。本文提出ISM和GAHP的评价方法,利用ISM构造系统层次结构,利用GAHP进行定量评价,系统地解决了这一问题。
1 基于ISM和GAHP的武器选型评价方法建模
1.1 解释结构模型ISM
1973年,为了分析更复杂的社会经济体系问题,美国J·华费尔教授研究了一种新型方法,称之为解释结构模型(interpretative structural modeling,ISM)。该方法以人类的实践经验和工程理论知识为基础,充分利用计算机辅助设计软件,将复杂的系统进行逐层分解,形成由若干个子系统(要素)构成的多级递推的结构模型,并据此分析各系统构成要素间的相互联系的程度[1]。已有一些文献对此方法在多个领域的应用进行了研究[2-5]。
1.2 灰度层次分析法GAHP
灰度层次分析法(grey analytic hierarchy process,GAHP)是一种量化定性指标的方法,用来反映评价指标的层次结构和每个组件之间的内在联系。运用灰色聚类分析方法,充分挖掘和使用少量的已知信息,尽可能构造完善的数学模型。计算不同聚类指标的白化数,然后对几个灰度级进行综合、归纳,确定所属的聚类,最后得出系统的综合评价[6]。关于GAHP的应用,已有一些相关研究[7-16]。
1.3 武器选型评价方法建模
基于ISM和GAHP的武器选型评价方法主要适用武器系统方案论证初期,是一种定性与定量相结合的方案评价与选择的方法。主要思路是:应用ISM思想,采用头脑风暴与专家评估,确定系统的功能结构与指标层次关系;在此基础上,应用GAHP思想,通过专家组对比决策,获得各指标的评价权重,以及各方案的评分,最后获得各方案的综合评分,从而选出最优方案。
基于ISM和GAHP的武器系统选型评价方法实现流程如下:
1) 选择系统要素S
根据系统概念设计和初步方案设想,经专家组分析和讨论,确定功能要求和技术途径,形成系统要素集S。
S={Si|i=1,2,…,n}
(1)
式中:Si为i个系统要素。
2) 建立邻接矩阵A
邻接矩阵A(adjacency matrix)表达系统要素之间的相互作用关系,经专家组研讨确定。
A=[aij]n×n
(2)

3)建立可达矩阵R
可达矩阵R(reachablity matrix)表达系统要素之间是否可以到达的状态。
R=[rij]n×n
(3)

R可以通过A加上单位矩阵I,按照布尔运算法则得到。
定义Ar-1=(A+I)r-1,若存在
A1≠A2≠…≠Ar-1=Ar,r≤n-1,则
R=Ar-1=Ar
(4)
4) 可达矩阵分级
对于要素Si,R中对应于Si的行中,所有要素为1的列所对应的要素Sj构成Si的可达集R(Si);R中对应于Si的列中,所有要素为1的行所对应的要素Sj组成Si的前因集A(Si)。若
R(Si)=R(Si)∩A(Si)
(5)
则Si为本级中最高级要素,组成集合L1。将L1中的要素从系统要素集中删除,再从余下的要素集中寻找次一级最高要素,直至把所有要素全部完成化级,逐级形成集合L2,L3,…,Lk,则级划分
ΠL(S)={L1,L2,…,Lk}
(6)
依据ΠL(S)要素顺序,对可达矩阵R进行变换,形成新可达矩阵R′
(7)
5) 构建缩减可达矩阵R″
进一步分析可达矩阵R′,若对角子阵Nkk为单位矩阵,表明其无回路;若对角子阵Nkk为满阵,表明其存在回路,在回路中选择一个代表要素,去掉其余要素,获得缩减可达矩阵R″。
6) 构建系统层次结构模型

当所有的子阵处理完毕后,即可获得武器系统层次结构模型,底层元素为武器系统的评估指标集合C
C={ci|i=1,2,…,m}
(8)
式中:ci为第i个评估指标。
7) 确定指标的权系数向量Λ[17]
专家组对待评估目标m变量按其相对重要性两两相互比较打分,构建判断矩阵B
B=[bij]m×m
(9)


根据判断矩阵B,求解权系数向量Λ
Λ=[λ1,λ2,…,λm]T
(10)
式中
获得权系数向量Λ后,需进行一致性判断。其中λmax表示判断矩阵的最大特征值,CR表示一致性指标。分别对其进行计算
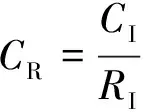
(11)

RI为平稳随机一致性指标[18]。
若CR远远小于0.1,则认为其一致性符合需求,此矩阵具有较好的一致性,得到的权系数值满足要求,否则,需对B进行必要调整。
8) 计算指标评估值矩阵D
获得指标权系数向量Λ后,对待评的p个方案,组织q名专家组按指标集C中各指标要素逐一对待评方案先进性进行打分,最低0分,最高9分,获得指标评估矩阵D

(12)

9) 确定评估灰度f
某受评指标c的评估灰度f主要包含灰度等级数、灰度的灰数、灰度的白化权函数。常用的白化权函数有下述3种[19-20]。
(1) 第一级“高”(e=1),灰数1⨁∈[d1,∞],白化函数为:

(13)
(2) 第二级“中”(e=2),灰数2⨁∈[0,2d2],白化函数为

(14)
(3) 第三级“低”(e=3),灰数3⨁∈[0,d4],白化函数为

(15)
10) 计算灰度矩阵X及灰度系数矩阵T
对某受评指标,应用e个灰度白化函数f,以及指标评估矩阵D,计算其灰色矩阵X(c)
X(c)=[xij]p×e
(16)

指标ci的灰度评估系数矩阵T(c)
T(c)=[tij]p×e
(17)

11) 计算灰色评估矩阵U
依据指标灰度评估系数矩阵T(c),按照最大化原则,可以获得m个指标的p个方案的灰色评估矩阵U
U=[uij]p×m
(18)

12) 计算综合评价值W
综合评价值W
W=UΛ
(19)
2 某机载武器系统选型评价应用示例
1) 选择系统要素
根据某机载武器系统论证需求,成立一个有行业研究经验的论证小组,根据机载武器系统作战需求以及当前技术发展现状,采用头脑风暴等方法,立足作战使用、装备保障、研制可行性等装备全寿命周期的能力需求,提出了24个决策要素,构建了机载武器系统要素集S,见表1。

表1 某机载武器系统要素集
2) 建立邻接矩阵
专家组结合其他同类产品要素作用关系,逐一分析,确定了各要素的作用关系,如S2与S1有关,a21=1,与其他要素无关,a2j=0;建立邻接矩阵A如下

3)建立可达矩阵R
按(4)式进行布尔运算,获得可达矩阵R

4)可达矩阵分级
计算各要素的R(Si)、A(Si)以及R(Si)∩A(Si),详见表2。

表2 某机载武器系统可达集、前因集
按(6)式判断要素层级,依次得到
依据ΠL(S)要素顺序,对可达矩阵R进行变换,形成新可达矩阵R′

5) 构建缩减可达矩阵R″
对可达矩阵R′进行分析,其不存在回路,则缩减可达矩阵R″=R′。
6) 建立结构模型


图1 机载武器系统结构模型
从图1可知,通过解释结构模型的计算、排序,某机载武器系统要素构成了一个4层结构模型。
第1层为综合评价层,由系统要素“综合效能(S1)”构成。综合评价层一般作为决策机关关注重点,用于项目决策及选型。
第2层为能力评价层,表征了全寿命周期的核心能力,由系统要素“作战能力(S2)、装机保障能力(S15)和可研制性(S21)”构成。能力评价层一般作为项目管理机关关注重点,用于项目方案的综合评价及全寿命管控。
第3层为性能评价层,表征了装备战术性能,由系统要素“威力(S9)、精度(S4)、持续作战能力(S5)、可装机性(S16)和适航性(S18)”构成。性能评价层一般作为型号研制总师关注重点,用于装备研制关键参数控制。
第4层为技术评价层,表征了装备战术指标,由系统要素“口径(S3)、初速(S6)、射速(S8)、立靶精度(S7)、自校靶能力(S10)、再射击时间(S11)、备弹量(S14)、寿命(S23)、后坐力(S12)、质量(S17)、综合保障性(S13)、安全性(S24)、技术可行性(S19)、发展潜力(S20)和全寿命周期费用(S22)”构成。技术评价层一般作为装备设计与验收人员关注重点,用于研制过程的技术实现及风险管控。
7) 计算评价指标的权重
对于第一层次“综合效能”的“作战能力、装机保障能力、可研制性”3个要素,组织专家组建立判断矩阵B1
按(10)式计算权Λ1
Λ1=[0.588 9,0.251 9,0.159 3]T
按(11)式计算判断矩阵的最大特征值λmax和一致性指标CR
λmax=3.053 9,CI=0.0270,CR=0.051 8
CR≤0.1,矩阵的一致性满足要求,权系数值可行。
同理计算第二、第三层指标构成要素的权系数,不同之处在于,所得权系数上乘以上一级的权系数,最终获得对第一层的权系数。
Λ21=[0.252 4,0.252 4,0.084 1]T
Λ22=[0.167 9,0.084 0]T
Λ23=[0.115 2,0.030 8,0.013 3]T
Λ311=[0.018 6,0.071 4,0.162 4]T
Λ312=[0.220 8,0.031 5]T
Λ313=[0.007 4,0.020 5,0.056 3]T
Λ321=[0.146 9,0.021 0]T
Λ322=[0.056 0,0.028 0]T
根据层次分析,选择底层要素3,6,8,7,10,11,14,23,12,17,13,24,19,20,22共15个要素进行综合评价,其权系数Λ为
利用权系数Λ绘制指标-权重图,见图2。

图2 机载武器系统指标-权重
从图2可知,初速(S6,0.071 4)、射速(S8,0.162 4)、立靶精度(S7,0.220 8)3个指标权重较高,对作战能力的贡献主要体现在单位时间内快速(射速)、精准(立靶精度)发射高威力弹药(初速)技术上;后坐力(S12,0.146 9)权重较高,对装机保障能力的贡献主要体现在降低后坐力对载机的冲击、振动载荷,提高载机与武器的兼容性上;技术可行性(S19,0.115 2)权重较高,对可研制性贡献体现在装备可实现性上,这几个指标应当被武器装备研制者高度关注,并不断迭代提升。
8) 计算指标评估矩阵D
组织专家组按指标S逐一对待评方案先进性进行打分获得指标评估矩阵D,其中
以及D(6),D(8),D(7),D(10),D(11),D(14),D(23),D(12),D(17),D(13),D(24),D(19),D(20),D(22)。
9) 确定评估灰度f
根据系统特点,选择4级灰度(“中”选择2级),第一级“高”(e=1),d1=9,灰数1⨁∈[9,∞];第二级“中”(e=2),d2=8,灰数2⨁∈[0,16];第三级“中”(e=3),d3=6,灰数3⨁∈[0,12];第四级“差”(e=4),d4=1,d5=5灰数4⨁∈[0,5]。
10) 计算灰度矩阵X及灰度系数矩阵T
对受评指标“口径”,应用灰度白化函数f,以及评估指标矩阵D(3),按(16)~(17)式计算其灰色矩阵X(3)、灰度评估系数矩阵T(3)
同理,可计算其他指标灰度矩阵X及灰度系数矩阵T。
11) 计算灰色评估矩阵U
依据指标灰度评估系数矩阵T(A),按(18)式计算灰色评估矩阵U为
利用灰色评估矩阵U绘制指标-灰度评估值图,见图3。

图3 机载武器系统指标-灰度评估值
12) 综合评价值W
按(19)式计算综合评价值W
结果可知,方案3比方案1、方案2更加优异。
从图3可知,在不计及指标权重的情况下,方案3初速(S6)、射速(S8)、立靶精度(S7)、后坐力(S12)等核心指标的灰度评估值明显优于方案1和方案2,抓住了武器研制的核心指标;同时自校靶能力(S10)、寿命(S23)、重量(S17)、综合保障性(S13)、安全性(S24)以及发展潜力(S20)也优方案1和方案2,其对指标的平衡性也是予以重点关注。从综合评价值看,计及指标权重的情况下,方案3之所以获胜,一是紧紧把握了关系武器系统成败的关键指标予以突破;二是同步全面、均衡发展其他技术指标,确保综合性能不仅局部最优,而且全域最优的设计思想。
3 结 论
基于ISM和GAHP的武器系统选型评价方法解决了武器装备论证初期系统方案择优的问题,可提高武器装备论证的水平。特点如下:
1) 利用ISM方法,将复杂系统的多要素的关系进行结构化、层次化梳理,层次结构图表征了参量之间的相互影响关系,揭示了构成武器系统的最底层要素;
2) 利用GAHP方法,定量描述了影响上一级要素,以及最上一级要素的要素之间的重要程度,给装备研制全寿命周期过程控制、资源投入、性能验证等工作指明了方向;
3) ISM和GAHP方法将定性描述转化为定量描述过程中,引入多人专家组的打分系统,并对偏离中心的差异性得分进行了加权处理,避免了专家个人的主观偏离对评价结果公正性的影响。
