计及网损的电网连锁故障预防方法

邓慧琼，王晓铭，ABDALAZIZ ALTAYEB IBRAHIM OMER，陈世举，钟运恒

(1.智能电网仿真分析与综合控制福建省高校工程研究中心(福建工程学院)福州 350118；2.福建工程学院 电子电气与物理学院 福州 350118)

为防止电网连锁跳闸，研究人员们建立了众多研究连锁故障的模型，并且深化融合了新的理论和方法提出了新的研究视角。如文献[1]在改进自组织映射聚类算法的基础上提出连锁故障预防模型，但并未评估预测结果的风险。文献[2]针对输电线路的脆弱性通过分析风险理论和复杂网络理论构建提出了一种评估方法，提升了搜索效率。文献[3]提出的新模型考虑了场站型和分布式新能源，但是对于新能源如何以最优的方式并网无法确定。文献[4]在分析社交网络的基础上结合连锁故障线路的影响力，提出一种能辨识连锁故障关键线路的方法，但是关于输电元件的重叠影响并未加以考虑。文献[5]对状态空间分割法进一步完善，通过枚举法和抽样法搜索连锁故障并分析其面临的风险，但是未考虑继电保护误动的情况。

上述研究都没有考虑到电网的电能损耗问题，本研究针对该问题以及电网的连锁跳闸，提出一种计及网损的预防控制方法，并优化了模型和算法。

1 网损的表达式

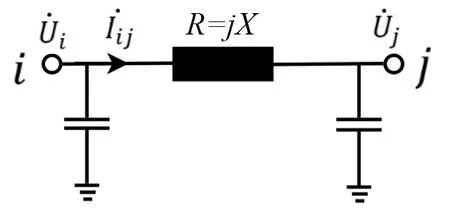
图1 支路Lij的等值电路图

总网损PLoss可用式(1)计算。

(1)

式中，Ω为所有支路集合，Ui为节点i的节点电压幅值，Uj为节点j的节点电压幅值，θ为电压相角差，R为支路的电阻，X为支路的电抗。

2 连锁跳闸的安全裕度表示

Iijdist=|Iijset|-|Iijm|

(2)

式中，Iijset和Iijm是与支路对应的电气量，Iijset是支路Lij上继电保护的整定值，Iijm是电力系统中电压和功率重新分配后支路Lij的实际测量值，Iijdist表示Iijset和Iijm之间的电气距离。由判别支路是否会发生故障的定义式可知，当Iijdist>0时，支路Lij不会发生故障仍能运行；当Iijdist<0时，支路Lij被继电保护切除，不再运行，即支路Lij可能会引起其他支路也发生故障；当Iijdist=0时，支路Lij处于将要发生故障和不发生故障的平衡状态。

当系统发生连锁跳闸，一开始发生故障的那条支路被切除之后，系统中剩下的支路是否会发生故障，可用式(3)进行判断。

m=min(Istdist)

(3)

式(3)同时也可以用来表示电网的安全水平，当m>0时，剩下的任何一条支路都不会出现故障，系统离发生故障还有一定的距离；当m=0时，剩下的支路中至少有一条处于将要发生故障和不发生故障的平衡状态，系统也处于将要发生故障和不发生故障的平衡状态；当m<0时，剩下的支路中至少一条会发生故障，系统对于连锁跳闸已经没有裕度。

3 计及网损的预防连锁故障模型

本研究以安全裕度尽可能大而网损尽可能小为预防连锁故障的目标，据此建立如下多目标优化模型。

根据网损要尽可能小的要求建立目标函数如式(4)。

f1=minPLoss

(4)

当电网结构和系统元件参数固定时，电网各支路的运行参数I是由电网的节点注入功率决定的，因此如果调整发电机的出力，使式(3)中的m保证能大于0，并且使m的值尽可能大，才能对电网的连锁跳闸起到有效的预防，提出如式(5)所示的目标函数。

在我国的林业产业建设中，林场经营和建设具有重要的地位和作用。在一段时间内，我国的林场经营管理存在一定的问题，即不重视养护，而只重视移植，种植之后的管理工作不到位，这造成林区存在一定的安全隐患。如很容易发生火灾、病虫害等问题，这种情况严重影响了林业的可持续发展和林业经济的发展建设。本文阐述的主要内容是我国林业管理过程中存在的问题，同时对管理工作的意义和提升管理质量的措施进行了简要的阐述。

f2=max(m)

(5)

将上述的两个目标函数f1和f2，采用均衡权重法，权重系数各取0.5，把多目标函数转换成式(6)所示的单目标函数形式。

(6)

给该目标函数加上等式约束和不等式约束[7]，便是完整的优化模型。

等式约束为初始故障发生前后电网满足稳态运行的潮流约束条件，用式(7)来表示该潮流约束。

(7)

式中，h0为初始故障发生前电网潮流对应的映射关系，h1为初始故障发生后电网潮流对应的映射关系，x为电网的状态变量。

不等式约束用式(8)来表示，包括发电机功率不等式约束，节点电压不等式约束，线路功率不等式约束。

(8)

其中，PGi和QGi分别为发电机功率不等式约束中发电机组的有功和无功出力，UK为节点电压不等式约束中任一节点k的电压，Pm为线路功率不等式约束中表示任一支路m传输的有功功率，将式(8)写成缩略形式，如式(9)所示。

(9)

其中，g0代表初始故障前的不等式约束，g1代表初始故障后不等式约束。

式(3)中的m应该大于0，而m也是状态变量x的函数，因此将m>0改写如式(10)的形式。

f(x)≥0

(10)

完整的优化模型如式(11)所示。

(11)

4 优化模型的求解思路

鸟群外出觅食时，要互相协作，分享信息，粒子群优化算法[8-9]就是基于这种思想来寻找最佳的解。该算法也适用于求解本文的优化模型，其迭代公式如式(12)所示[10]。

(12)

式中，v(t)代表速度，vmin和vmax为速度的限值；x(t)代表位置；P(t)代表粒子群中某个个体的最优值；g(t)为整个粒子群的最优值；w为惯性因子，c1和c2为加速因子；r1和r2取的是区间[0,1]上的随机数。

把式(11)中h0(x)=0，h1(x)=0交给潮流计算去处理，若计算结果无法满足，则生成新的粒子。其余约束改成式(13)所示[11]的具有惩罚因子的形式。

F1=F+M[max(0,g0(x))]2+

N[max(0,g1(x))]2+Z[max(0,f(x))]2

(13)

式中，M、N、Z均为惩罚因子。

5 算法流程

粒子群算法求解的主要步骤为切除故障初始化粒子群后分别计算每个粒子的网损与安全裕度，具体的算法结构流程如图2所示。

图2 算法流程图

6 算例分析

以IEEE-39节点系统为例，对所提方法进行分析验证，其系统接线图如图3所示。

图3 IEEE-39节点系统接线图

通过MATLAB编制所需的程序，系统中各种参数都设为标幺值，包括F1和F也设为标幺值，基准容量设为100 MVA，电力系统中配置的继电保护是保护电流定值设为5.77 kA的电流型后备保护。

设初始故障支路为支路L10，其首末端节点分别为5和8，当切除支路L10，电网中电压和功率重新调整后，通过粒子群算法进行200次的迭代计算得以求解。

其中f1、f2对应的数据与安全裕度值对应的数据分别如图4、图5所示。

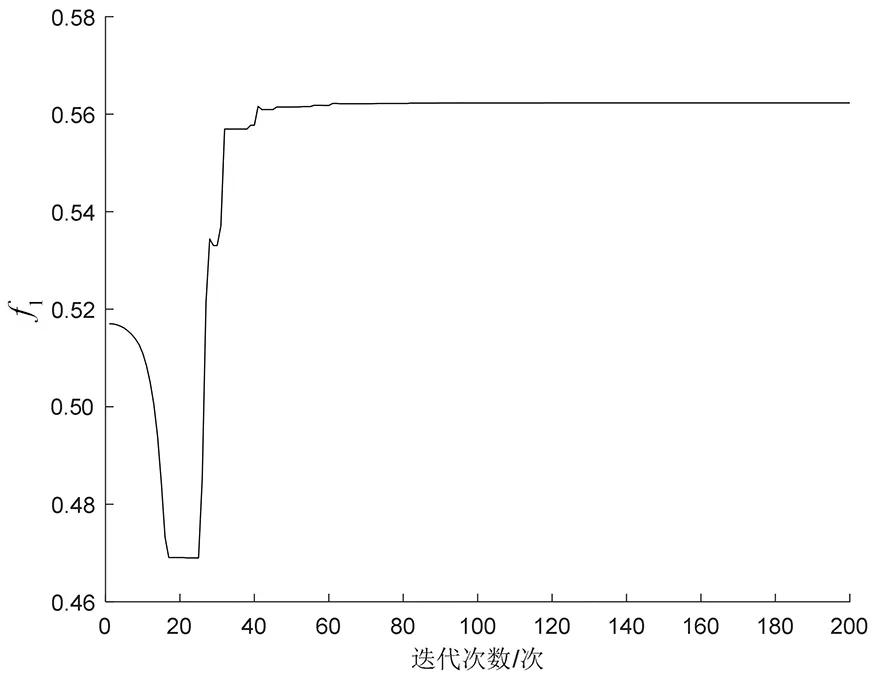
图4 f1的数据

图5 安全裕度值

从图4曲线的变化可以看出，f1的数值在25代之前逐渐减小并在17代至25代之间趋于一恒定值后渐渐提升，从80代开始，变化渐渐平缓并处于一恒定值不再变化。

从图5的曲线变化可以看出，安全裕度的值逐渐提高，在17代至25代之间趋于一个恒定的值后又继续上升，80代之后渐渐平缓，即安全裕度已经优化到最大值。

由此可知，在安全裕度提高的过程中，网损确实有所降低，在25代之前，安全裕度从1.869 3提高到了2.369 4，而网损从0.517 0减少到0.469 0。但是如果安全裕度继续提高，那么网损也将随之提高，最后安全裕度优化到最大值2.899 3，此时对应的网损为0.562 3，虽然网损有所增加但是变化不大。这是综合之后较好的结果，即提高了安全裕度而网损处于比较低的结果。

7 结论

本研究考虑电能损耗以及电网的安全运行，提出了预防连锁故障的模型和算法，经过分析验证，得出以下结论：

1)研究所建立的模型是多目标优化模型，对连锁故障的预防进行了多方面的考虑，既考虑了安全又考虑了损耗。

2)算例仿真结果表明在一定程度上随着安全裕度的提高网损会随之降低，但是不能得到安全裕度最大同时网损最低的结果，得到的结果是一个在均衡权重下相对综合的数值，即安全裕度高而网损较低的结果。