基于ARIMA的冬季日最低温度预测与分析

刘芳 葛瑞婷

（淄博市气象局 山东省淄博市 255000）

1 引言

随着社会的发展、经济的进步，天气预报对人们的生活、出行、农业及经济等方面所起到的影响越来越大。天气预报的重要特点之一就是时效性，人们需要提前知道，并根据预报信息来做出合理的安排、计划。如果在大风、暴雨、低温、高温、冰雹及暴雪等恶劣天气来临之前，假如相关部门、单位及群众提前获知天气并做好防御措施，这在一定程度上能够减少甚至避免一些人员伤亡和经济损失。正如郑州“7•20”特大暴雨发生后，许多专家学者对此过程做了分析和总结，针对不同城市特点提出了相应的防御对策，来防患于未然。因此，预测未来天气是气象领域一个至关重要的任务，天气预测就是对某一地点的大气运动状态来进行预测。它在气候监测、灾害性天气预测、农业、军事及交通等方面的应用都具有巨大的作用。

从古至今，人们从未停止过对天气变化趋势的研究与预测。观测方法由最初的人工观测演变为自动观测，这不仅减少了人力成本的投入，更重要的是摆脱了条件恶劣区域人工不能观测的困境，而且收集到的数据日渐增多。大量的气象数据为更加准确的预测天气要素奠定了坚实的基础。当然随着气象大数据时代的到来，原始的预测方法具有局限性。同时，天气过程是千变万化，且十分复杂的，单凭人工经验观测得到的准确率已不能满足现在人们、社会的需求。因此，目前也有许多物理预测法、基于统计学的方法、综合预测方法被提出和应用。物理预测法是利用气象理论知识，拟合大气运动函数，在明确初始值和边界条件的情况下对函数做积分计算，从而实现对天气要素的预测。基于统计学的方法主要利用数据统计分析方法，统计某一气象要素的数值在一段时间内出现的频率，从而推算出未来一段时间内，在相似环境条件下该气象要素出现的概率。郭等使用自回归模型来预测季节的降雨量。综合预测方法把不同的预报方法结合，从而获得更加准确的结果。

时间序列模型也是一种常用的预测方法之一。时间序列是指按照相同的统计指标并根据其发生的先后时间顺序排列而成的一组数据，而时间序列分析主要是根据已有的历史数据来对未来一段时间进行预测。差分整合移动平均自回归模型(Autoregressive Integrated Moving Average model，ARIMA)是最经典的时间序列预测模型之一，目前已有许多利用ARIMA模型来预测股票、经济走势、天气中温度、空气质量指数等气象要素的研究。

本文基于对日常的公共气象服务内容的分析，发现人们对于冬季（11月-次年2月）日最低温有强烈的需求，尤其对农业、交通、供热公司等部门有重要的作用。例如，对于高速公路修建公司，他们需要提前知道当年进入冬季的时间，需要确定大约在哪个时间温度低于0℃，因为他们需要在低于0℃的严冷天气的前期，为一些怕冻的材料、机器及路面做好保护，为停工做准备，以防造成冻灾，减少或者避免造成经济损失。因此，本文主要关注于利用ARIMA模型来预测未来年份的冬季日最低气温。本文收集了山东省某市1990-2021年10、11和12月、1990-2022年1、2月日最低气温做训练数据集，来评估ARIMA预测该市冬季日最低气温的性能。本文根据使用的历史时间序列数据的不同，给出了两种预测方法。首先，ARIMA利用预测月份的上个月的日最低温数据来预测该月份的数据值，如利用1990年10月1-31日真实的日最低温来预测1990年11月1-30日的日最低温，该方法称为ARIMA_LM(ARIMA based on Last Month data)。其次，为了预测距当前时间更长久时间的冬季日最低温度，本文利用1990年-2021(2022)年所有跟预测月份、日数都一致的数据来预测未来年份的该月和日的最低温。假如要预测2022年11月1日的最低温时，需要统计1990年-2021年中每年11月1日的数据值来完成预测，该方法称为ARIMA_D(ARIMA based on Daily data over the past years)。最后，通过实验分别评估了ARIMA_LM和ARIMA_D的准确性，并利用ARIMA_D方法预测了山东省该市未来一年冬季日最低温度。

2 基于ARIMA的冬季日最低温度预测

2.1 ARIMA模型

ARIMA模型主要由自回归(AR)模型、移动平均(MA)模型和差分模型组合而成，是一种有效的时间序列预测模型之一，表示为ARIMA(p,d,q)，其中p、q、d分别为AR、MA、差分模型中的参数。因此，接下来主要介绍差分法、AR、MA和ARMA模型。

2.1.1 差分法

在实际生活中，获取的大部分时间序列数据分布是各种各样的，但是要预测未来一段时间的数据值，就要求这个时间序列数据具有一种惯性，即需要该时间序列数据是平稳的。

定义1 时间序列数据的平稳性。随机生成一个时间序列{Y}(t=1, 2, …)，{Y}中的每一个数值是从一个概率分布中随机获得的。如果{Y}满足下列条件：

（1）均值E(Y)=a，a是跟时间t无关的常数;

（2）方差Var(Y)=S，S是与时间t无关的常数；

（3）协方差Cov(Y, Y)=v，v是只与时期间隔k有关，与时间t无关的常数。

也就是说，平稳性时间序列数据的均值和方差不随时间变化而发生明显变化。

为了让一个非平稳的时间序列数据呈现出平稳性，本文采用差分法：

给定时间序列数据Y(t=1, 2, …)，差分后的时间序列F满足以下条件：

（1）F=Y-0，当t=1时；

（2）F=Y-Y，当t≥2时。

利用Y中的每个数据与其前一项的差值，来得到差分后的时间序列数据F的方法，称为差分法。做一次差分操作称为一阶差分，d次差分称为d阶差分。此外，当Y做一阶差分获得的时间序列数据F依然不具有平稳性，可以对F再做一次差分操作，一次类推，直到得到平稳的时间序列。

2.1.2 自回归(AR)模型

自回归模型描述的是当前值与历史值之间关系，利用其自身的历史数据来对未来进行预测，这就要求自身的历史数据满足平稳性的条件。

AR模型表示为：

其中，μ是常数项，p为阶数，表示当前值与前p个历史值相关， ε为误差，γ为自相关系数。

2.1.3 移动平均(MA)模型

MA模型主要是自回归模型中误差项的累加，是为了有效地消除AR模型的随机波动。MA模型表示为：

其中，μ是常数项，q为阶数， θ为参数。

2.1.4 自回归移动平均(ARMA)模型

假设在任意时刻t的数值为y，与历史时间点的自身相关的同时，还需与历史时刻影响模型的误差也存在一定的相关性，满足上述特点的模型称为ARMA(p,q)模型。实际上，ARMA(p,q)模型是自回归模型AR(p)和移动平均模型MA(q)的组合，表示为：

因此，ARIMA模型是将非平稳时间序列转化为平稳时间序列，然后将因变量的前p阶数值、随机误差项的现值和前q阶误差值，进行回归建立的预测模型。

2.2 选取参数p，q值

对于AR模型和MA模型中的参数p，q，通过利用自相关函数(Autocorrelation Function，ACF)和偏自相关函数(Partial Autocorrelation Function，PACF)求得。ACF是衡量时间序列中间隔k个时间范围(y与y之间)观测值间的相关性，表示为：

也就是说，ACF是y和y之间的协方差与y方差的比值。

而PACF是剔除了中间k-1个随机变量y，y，y......y的扰动，仅保留y对y的相关性。

本文首先计算ACF和PACF，对于AR(p)模型中参数p，满足偏自相关函数的p阶落在置信区间内(也称为p阶截尾)，自相关函数随时间t的增加而衰减趋于零，如表1中第二行。MA(q)中参数q，满足ACF是q阶截尾，PACF也呈现衰减趋于零的趋势，如表1中的第三行。

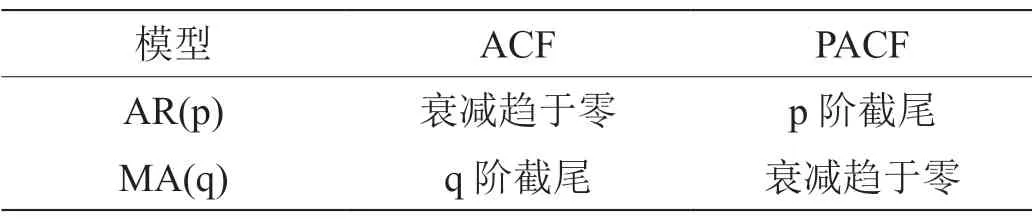
表1：参数p、q取值

2.3 ARIMA_LM方法和ARIMA_D方法

2.3.1 ARIMA_LM方法

本小节详细地描述了ARIMA_LM方法(ARIMA based on Last Month data)的过程，如算法1所示。

算法1：ARIMA_LM方法

Input：Historical dataset HD，forecast days n；

Output：predicted value for n days

（1）ini(HD) ←preprocessing dataset HD

（2）d-difference method for HD

（3） p、q←compute ACF、PACF

（4） Build model ARIMA(p,d,q)

（5） optimize model ARIMA(p,d,q)

（6）return Set

首先，预处理历史时间序列数据，剔除异常值、空值等（如1）所示；然后，对历史时间序列数据HD进行差分处理，使其具有平稳性（如2）所示；之后，计算d阶差分后的HD的ACF、PACF，来确定AR(p)、MA(q) 模型中的参数p、q（如3）所示，最后建立、优化ARIMA，并返回预测的未来n天数据值集合Set（如4-6）行所示。

2.3.2 ARIMA_D方法

本小节给出了ARIMA_D方法(ARIMA based on Daily data over the past years)的过程。

算法2：ARIMA_D方法

Input：Historical dataset HD，forecast days n；

Output：predicted values

（1） ini(HD) ←preprocessing dataset HD

（2）for p∈HD do

（3） p←time index of p

（4） day←segmentDay(p)

（5） Set←Set∪{p}

（6）for Set∈Setdo

（7） d-difference method for Set

（8） p、q←compute ACF、PACF

（9） Build model ARIMA(p,d,q)

（10） optimize model ARIMA(p,d,q)

（11） p←predict by ARIMA

（12） Set←Set∪{p}

（13） return Set

该方法主要适用于已有20、30年甚至更久的历史时间数据，采用几十年具有相同月份、日数的数据来预测未来该月份、日数的数据值，如通过1990-2021年每年11月1日的历史数据来预测2022年11月1日的数据值。首先，预处理历史时间序列数据，剔除异常值、空值等，如（1）所示；然后，针对历史时间序列数据集HD中的每个对象，提取其时间索引中的日数（如2019年11月01日，日数为01；2019年11月18日，日数为18，记为day，并按照day存放到相对应的集合Set中。也就是，把日数相等的数据对象放到一个集合，如（2）-（5）所示。之后，依次对每个集合Set进行差分处理，使其具有平稳性，对平稳后的时间序列数据计算ACF、PACF，来确定AR(p)、MA(q) 模型中的参数p、q。接下来，建立、优化ARIMA，并把预测的未来一年该月份且日数为day的数据值存放到预测集合Set中，如（6）-（12）所示，最终得到未来一年该月的预测数据值。

3 实验评估

本文主要采集了山东省某市1990-2021年10、11、12月、1990-2022年1、2月每日最低气温作为实验数据集。本文采用90%的数据作为训练数据，10%的数据作为测试数据，来验证所提方法的准确性。

3.1 预测有效性评估

本小节主要利用准确率和平均绝对误差(Mean Absolute Error，MAE)来衡量ARIMA_LM和ARIMA_D方法预测该市冬季日最低温的准确性。

3.1.1 正确性评估

本小节评估了所提方法预测该市冬季日最低温的准确率，准确率=((R∩D))⁄D，其中R表示所提方法预测的时间序列集合，D表示当前预测时间段中真实的数据值集合。首先，本文分别给出了ARIMA_LM方法预测2019、2020、2021年11、12月，2020、2021、2022年1、2月前5天（1-5日）、10天（1-10日）、15天（1-15日）、20天（1-20日）及1个月的准确率，见图1。

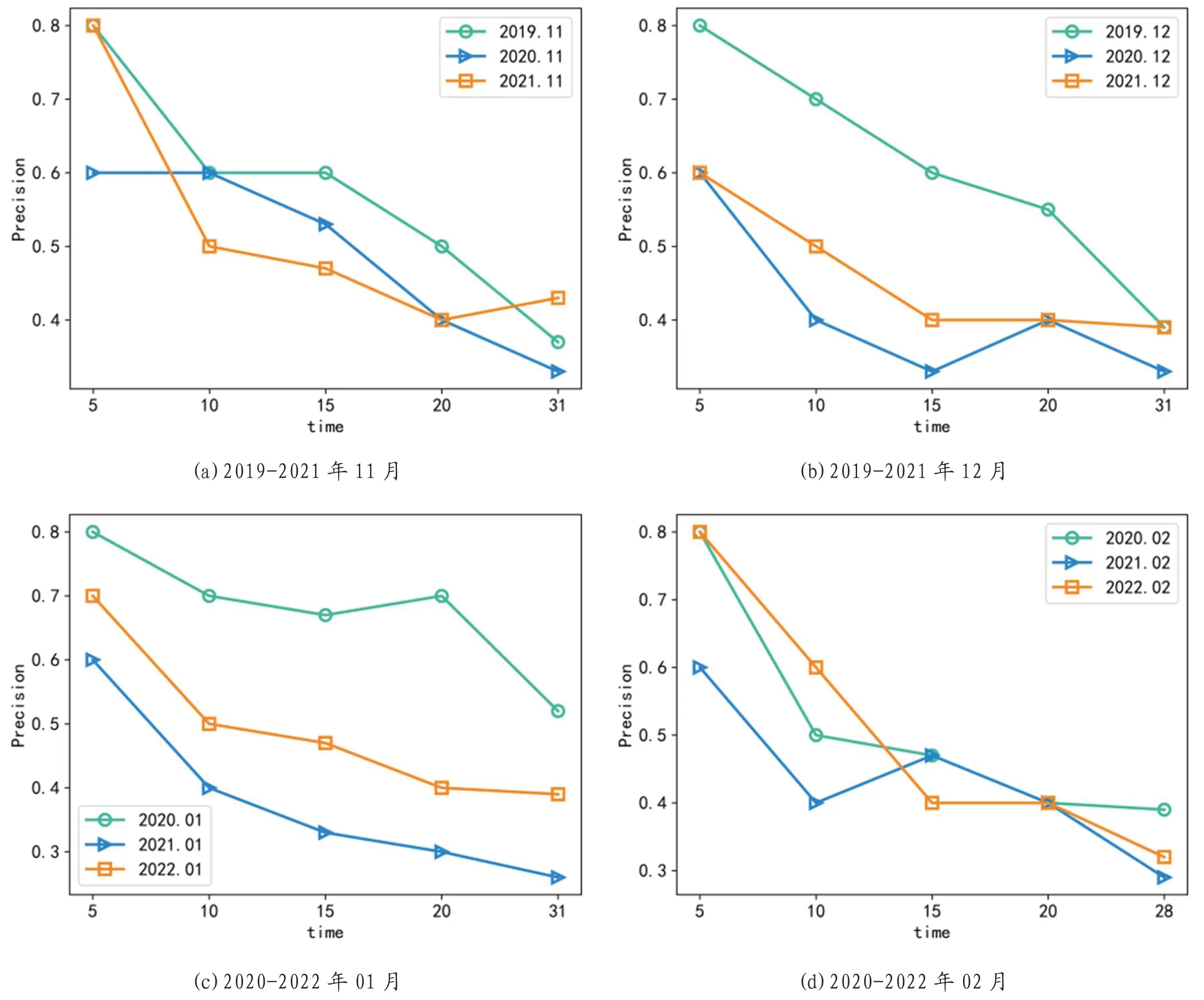
图1：ARIMA_LM预测准确率

从图1中可以看出，预测2019、2020、2021年11月前5天（1-5日）的准确率分别为80%、60%、80%（如图1(a)）；2019、2020、2021年12月1-5日准确率分别为80%、60%、60%（如图1(b)）；2020、2021和2022年1、2月1-5日最高准确率可达80%，该准确率是接近甚至高于该市预报冬季日最低温的真实准确率。预测2019、2020、2021年11月 前10（1-10日）、15（1-15日）、20（1-20日）天及整月（1-30日）中最高准确率分别为60%、60%、50%、37%；同样，12月分别为70%、60%、55%、39%。2020-2022年1、2月前10天平均准确率为60%，而15、20天及整月的平均准确率分别为57%、55%、46%。

通过实验结果可以看到，预测未来的天数越多准确率越低，这说明如果预测的数据不是周期性、规律性的，预测长期的结果会受到前面预测有偏差，甚至错误结果的影响。因此，ARIMA预测短期数据比长期数据更加有效。

其次，图2展示了ARIMA_D方法预测2019-2021年11、12月及2020-2022年1、2月的准确率，图2中横坐标表示预测的月份。从图2中可以看到，准确率最高达60%，结合ARIMA_LM方法预测结果分析，可以获得预测某天的最低温度，与其临近该日的一段时间的最低温度相关性较大。

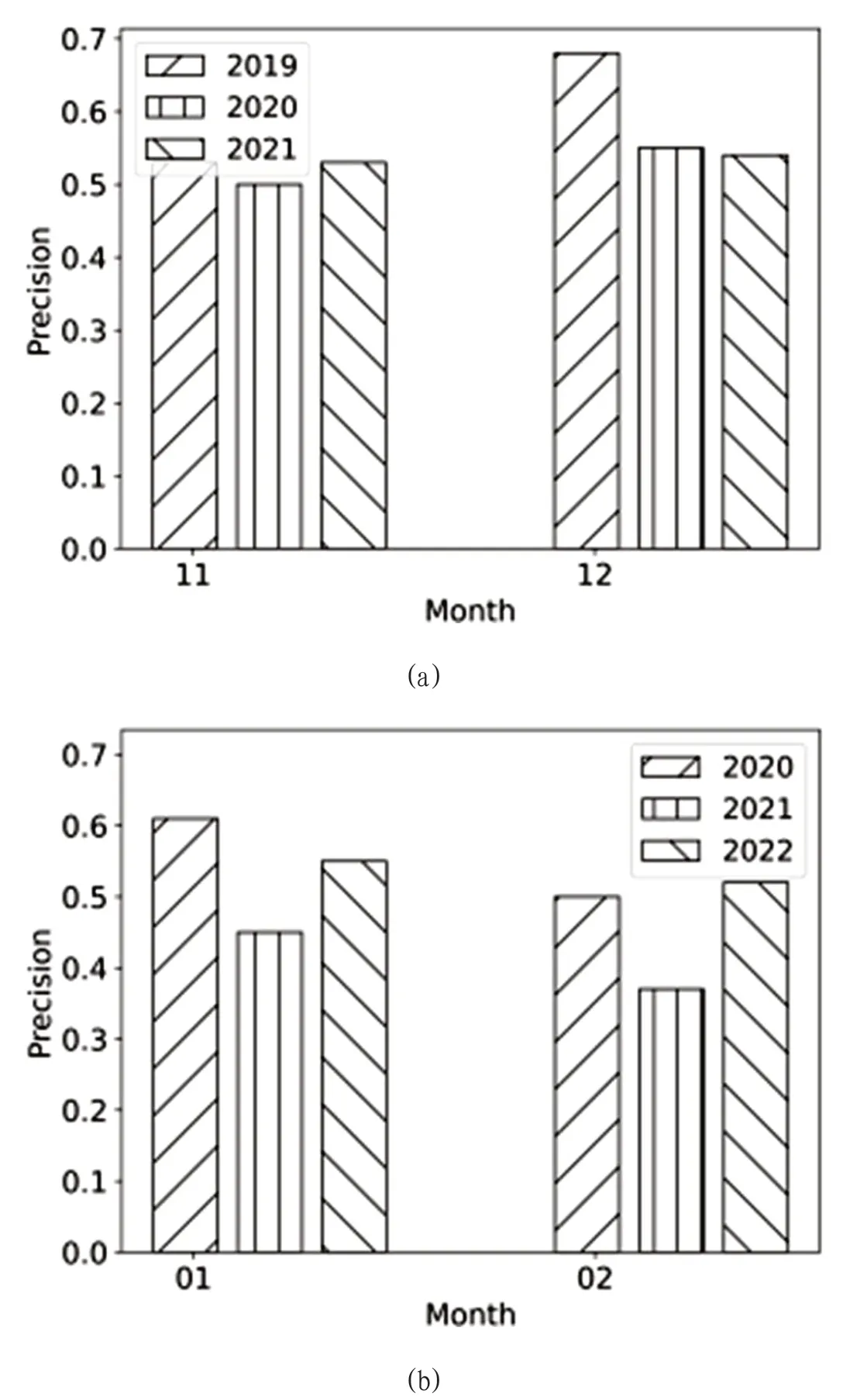
图2：ARIMA_D预测准确率

3.1.2 平均绝对误差评估

平均绝对误差(Mean Absolute Error, MAE)表示为：

其中，y是真实值，为预测值，n为预测天数。MAE值越小，说明预测值越接近真实值。

表2展示了ARIMA_LM方法预测一个月份不同天数的平均绝对误差值。第一列表示预测的年份、月份，第一行表示预测一个月的前5天、10天、15天、20天及整月的天数。第二行表示预测2019、2020和2021年11月前5天（1-5日）、10天（1-10日）、15天（1-15日）、20天（1-20日）及整月的平均绝对误差和的均值。同理，第三行是预测2019-2021年12月前5天、10天、15天、20天及整月的平均绝对误差值和的均值，第四行、五行分别表示预测2020-2022年01月、2020-2022年02月前5天、10天、15天、20天及整月的平均绝对误差值和的均值。

从表2可知，预测11、12、1、2月前5天的平均绝对误差值（第二列所示），相比预测11、12、1、2月前10、15、20天及整月的平均绝对误差值是最小的。随着预测天数的增多，其误差值也基本呈现增大趋势，最后一列是预测2019-2021年11月平均绝对误差均值和的均值、2019-2021年12月平均绝对误差和的均值，及2020-2022年1月和2月的平均绝对误差和的均值。这些值都大于预测相应月份中前5、10、15、20天中误差值最大的，这说明预测的天数越多，预测值与真实值偏差越大，准确率越低。

表2：ARIMA_LM预测不同天数误差值的均值

表3是ARIMA_D方法预测2019-2021年11、12月，2020-2022年1、2月的平均绝对误差值。第一列表示预测的年份，第一行是预测的月份。

表3：ARIMA_D预测整月的平均绝对误差值

对比表3 与表2的最后一列发现，表2中2019、2020和2021年 11月的平均绝对误差和的均值比表3中2019、2020和2021年 11月的平均绝对误差值都大。同样，表2中预测2019-2021年12月、2020-2022年1、2月的平均绝对误差和的均值大于表3中预测相同月份的误差值。这再次验证了ARIMA_LD前面天数预测得到偏差较大甚至错误的数据值，会导致后面预测值的误差越来越大。同时，也说明ARIMA_LD方法预测短期内的数据值更加有效，预测未来较长时间段的数据值，ARIMA_D方法比ARIMA_LD方法误差更小，效果更好。

3.2 预测最低温

据3.1.1和3.1.2节分析，本小节给出了利用ARIMA_D方法来预测未来一年冬季（即2022年11、12月，2023年1、2日）日最低温，见图3。横坐标表示每月中的日数，纵坐标表示预测的温度值。从图3可知，从11月23日左右开始进入零下气温模式，而12月大部分时间维持在零下，且基本上都低于-2.5℃。2023年1月平均温度最低，2月温度开始缓慢回升，从19日开始最低温有大于0℃的情况。

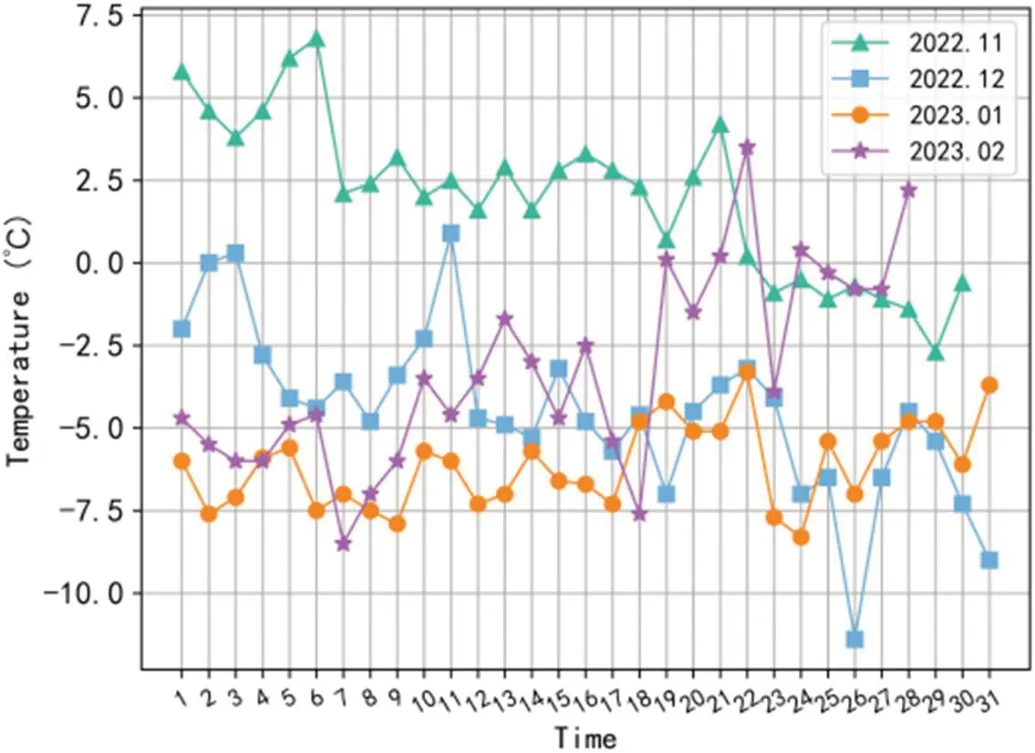
图3：ARIMA_D方法预测未来一年冬季日最低温结果

该预测结果可以提前几个月或更久的时间获知，能够粗略的预知未来年份最低温低于0℃的天气出现的时间，为提前准备防冻灾工作奠定基础。此外，在临近冬季的时候，可以采用ARIMA_LM方法来预测短期温度，获得更加准确的预测结果。

4 总结

本文主要利用时间序列模型ARIMA来预测冬季日最低温度，根据提前获得时间的长短不同，给出了不同的预测方法。第一种方法是ARIMA_LM，该方法主要用来预测近期未来时间段内的数据值。第二种为了提前几个月甚至更久的时间，预知未来年份冬季日最低温，提出了ARIMA_D方法。在真实数据集上实验发现，ARIMA_LM预测未来较短期的准确率可高达80%，而随着预测天数的增加，准确率逐渐降低。因此，在实际生活中，首先利用ARIMA_D方法提前几个月或更长时间，来预知冬季的日最低温，粗略的制定防冻灾措施，然后临近冬季的前几天或一个月，利用ARIMA_LM方法获得更加准确的预测结果，据预测结果合理调整防冻灾措施，从而进一步减少甚至避免因低温对农业、交通等各部门、公众造成的损失。