电磁发射用脉冲功率电源系统的参数分析

张哲 张子尧 钟岩 王思齐

（1.中国矿业大学孙越崎学院 江苏省徐州市 221000 2.中国矿业大学电气工程学院 江苏省徐州市 221000）

1844年Colonel dixonz首次提出了“电磁炮”的概念，紧接着哥伦比亚学院的Chars Wheastone教授建造的世界第一台直线磁阻电动机能够把金属棒抛射到20 m远处。2003年4月，美国海军用90 mm口径电磁炮样机发射了初速达2500 m/s以上的射弹，演示验证试验取得成功。由于关键技术和基本国情的影响，国内电磁炮起步较晚，不过在近几年国内电磁炮发展较为迅速，理论与实践均取得关键性突破。理论上清华大学常馨月使用遗传算法改良了脉冲触发电源的触发位置并提出多种方法能够较为准确的估测放点模块个数。实验方面中国工程物理研究院流体物理所和中国科学院在“第九个五年计划”对于电磁炮技术取得重大成果，研制的试验型发射器将质量为30 g和50 g的电枢加速到3000 m/s。目前我国的电磁轨道发射技术尤其在发射器技术、脉冲电源技术上进展显著，目前已经具备10 MJ级脉冲电源的发射平台。

本文对轨道炮电路拓扑结构、各组件受力及能量变化过程作出分析，并采用模块化方式分别搭建脉冲功率电源模型和轨道炮负载的动态数学模型，使用Simulink对电源电压及电容值、调波电感及多级电源时序变化进行仿真调试，观察各参数对峰值电流及电流脉宽的影响并给出结论，对电磁轨道炮系统脉冲功率电源提供了参数建议及方案选择。

1 电磁轨道炮基本原理

1.1 轨道炮结构

电磁轨道炮主要由脉冲功率电源、传送轨道、电枢和弹丸组成。在发射电源工作之前需要充电电源供给能量，电容器作为发射电源经过储能后，脉冲晶闸管得到触发信号，电路导通，高功率脉冲电源在短暂时间内提供瞬态或稳定的高功率场电流或驱动脉冲，电流经过轨道、电枢及负载后流回电源，轨道内因电流产生磁场，此过程中回路中的轨道会产生强大的电磁力，由于电磁力的影响，电枢推动弹丸作加速运动，弹丸会获得极大的初速度向外发射，电磁轨道炮结构图如图1所示，示意图如图2。

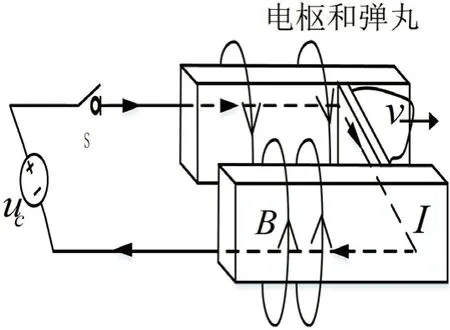
图1：电磁轨道炮结构图

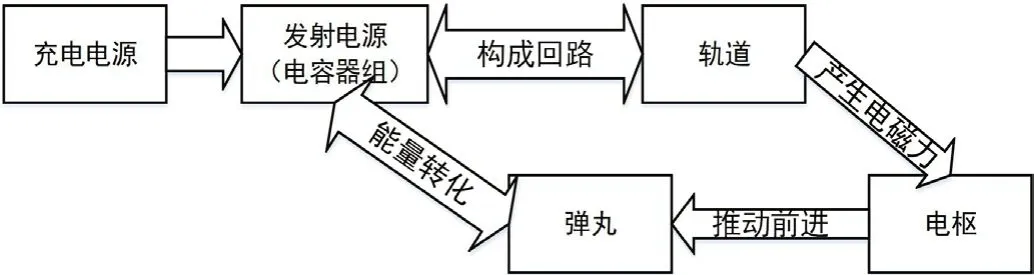
图2：电磁轨道炮示意图

1.2 电磁轨道炮重要元件

脉冲成形网络主要由初级电源、调波电感、半导体开关器件组成。为使弹丸可以加速到发射要求速度，这需要峰值电流稳定且达到额定工作值，设计时常使用多个不同时序电容器组作为发射电源。电磁炮期望工作电流波形为近似梯形波，只依靠电路中初始电感可能会造成电容释放能量后电流峰值时间过短，需要安装电感器调节电流波形。电路中的半导体开关包括晶闸管开关和续流硅堆二极管，前者在大电流大电压下，可适应高电流变化率，重复性能优良，允许电磁炮多次发射炮弹；后者的作用体现在续流过程，能够防止反向充电保护电源。轨道是电磁炮结构的核心部件，可传导电流，导向电枢和弹丸，作为电能向动能转化的枢纽，电枢的选择至关重要。电枢的常见形式是固体金属电枢、等离子体电枢、混合电枢、过渡电枢。固体金属电枢粘滞力和烧蚀力很小，电阻低，电压压降小，原理简单，是采用较为普遍的电枢。

2 轨道炮电路分析

图3为电磁轨道炮系统的脉冲形成单元（pulse forming unit, PFU）电路拓扑结构，u为电容器两端的电压；T为晶闸管开关，D为续流二极管；R、L分别是系统的电容杂散电阻、杂散电感；R、L为线路的杂散电阻和杂散电感；由于电容器直接对负载放电会产生窄脉宽的脉冲大电流，因此选用调波电感L来调节电流波形。R为调波电感等效电阻值；轨道炮负载连接在电路中，通常可看成阻感负载。

图3：PFU内部结构

发射过程可按照两种工作状态分类，分别为电容器放电过程和续流过程。

2.1 电容器放电过程

当晶闸管触发导通后，电容C开始放电，图4中u指电容的初始储能电压，此时电容器作为发射电源，向整个电路提供电场能量。二极管正向电压小于反向电压，其所在支路处于断路，在该过程中能量一部分被轨道电缆和各元件自身电阻以热量的形式散失，还有一些能量转化成以调波电感为主体的电感器储存的磁场能量，而剩余大多数能量由电枢转化成轨道炮负载的动能，少数被磨擦阻力、空气阻力消耗。放电过程中电容器电压不断下降，回路电流为上升趋势，将上述电感及电阻分别用整体L、R来等效表示,图像如图4。

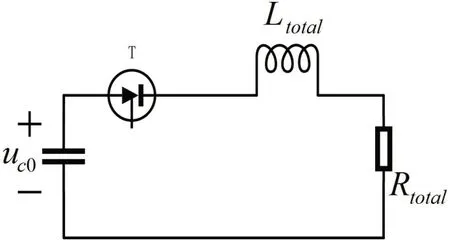
图4：RLC二阶时域电路

对图4电路，根据基尔霍夫定律可得到回路电压关系式（1），即初始储能电压和电容器释放电压差值即为回路中转移的各种能量和。

由于轨道炮负载呈感性，知该过程为二阶欠阻尼振荡，可得到式（2）：

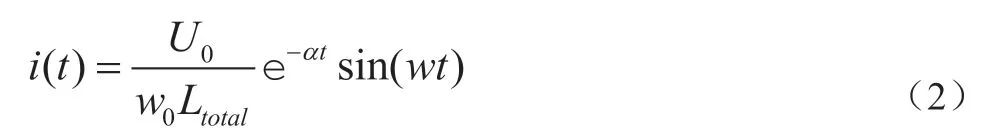
2.2 续流过程

电容器放电结束的标志为脉冲电流达到最大值i，该时刻为续流过程的零初始状态。当电容器电压接近0时，续流二极管此时正向电压大于反向电压，将电容器所在支路短路，有效避免对电容器C反向充电造成损坏，因电感的存在电流不会突然变化，而是逐渐减小，电感此时作为电源将储存的磁能一部分转化为炮弹动能，另一部分能量以热能的形式散失，当电感能量降至0附近时续流过程结束，电路图见图5。

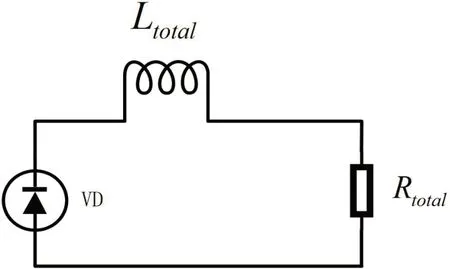
图5：RL一阶电路

根据基尔霍夫定律可得到时域和电压关系式：

电流达到最大值时刻即为续流过程的初始时刻，此时

3 电源参数的仿真分析

由上文对轨道炮电路分析得到的公式（2）、（4）、（5）、（6）可知，轨道炮峰值电流主要与电容器预充电压及电容值、调波电感、电源模块及不同模块晶闸管触发时序有关。以此作为依据设定基础参数值，建立脉冲功率电源的电路模型和轨道炮负载的动态数学模型，并在Simulink中进行联合仿真，具体参数设置如表1。本文通过控制变量法，通过理论逐一分析上述影响因素，观察随着时间的变化各因素对峰值电流和电流脉宽的影响。

表1：仿真模型的参数设定

3.1 电容器参数分析

3.1.1 电容器预充电压

根据放电电路分析可知，在理想情况下，预充电压与峰值电流应成线性关系，即电压增加的倍数和峰值电流应相同。在放电时间上，改变预充电压对于放电过程和续流过程的时间常数无影响，但是由于初始电压增大会使放电时间增加。仿真实验时，以1000 V为增量，将该参数取2000—6000 V五组数据，如图6所示。

从图6中的五组曲线可以看出，随着初始储能电压的增加，轨道炮峰值电流逐渐增大，脉宽和两过程时间比例均基本保持不变。其中在2000 V时达到峰值电流时间约为0.8 ms，电流为18.78 kA,4000 V时对应的峰值时间和电流幅值分别为0.88 ms，37.56 kA。电流幅值增加一倍，峰值时间近似相等。实际情况中，电磁发射会伴随一定的能量损耗，如发射电源的内部损耗、电枢与导轨的摩擦生热、电枢发射过程中发生刨削等，因此随着电容预充电压的升高，负载电流峰值近似成比例增加。

图6：电源预充电压参数特性

3.1.2 电容器电容值参数分析

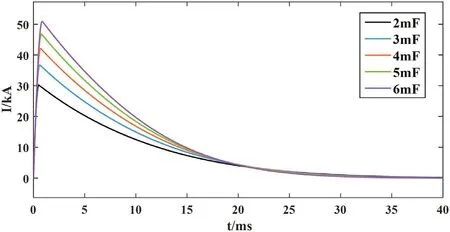
图7：电源电容值参数特性

根据上述分析可知，电容值和储能电压值越大，峰值电流越大，此时电枢——弹丸组件可以获得更高的加速度，而电流脉宽基本保持不变。但考虑到过高脉冲电流对炮管中各元件的损伤以及成本问题，电容器参数并不宜过大，应选取合理范围。

3.2 调波电感参数分析

模型中调波电感远大于电路其他部分的电感，因此本文主要研究电源中调波电感及其等效内阻对峰值电流的影响。仿真初始电感及增量均为10 uH,取五组仿真数据绘制曲线如下。由图8可知，电流脉宽随着调波电感的增加而增加，但峰值电流在不断减小。当调波电感提高到初始电感5倍后，电流峰值约由50.21 kA增至105.2 kA,倍数约为2.1倍。电流脉宽由于时间常数的影响，增大电感会使时间常数变大，延长电流持续时间，可以有效提高弹丸发射速度，附带电阻对脉宽的影响与此同理，如图9所示，等效内阻作为电源内部损耗的主要来源对电流峰值的影响不大，等效内阻越小，电流峰值越高。因此在选择调波电感的具体参数时，应保证调波电感处于合适区间、其附带电阻尽可能小从而在保证电流适中的情况下增加弹丸的加速时间，减少能量损耗。

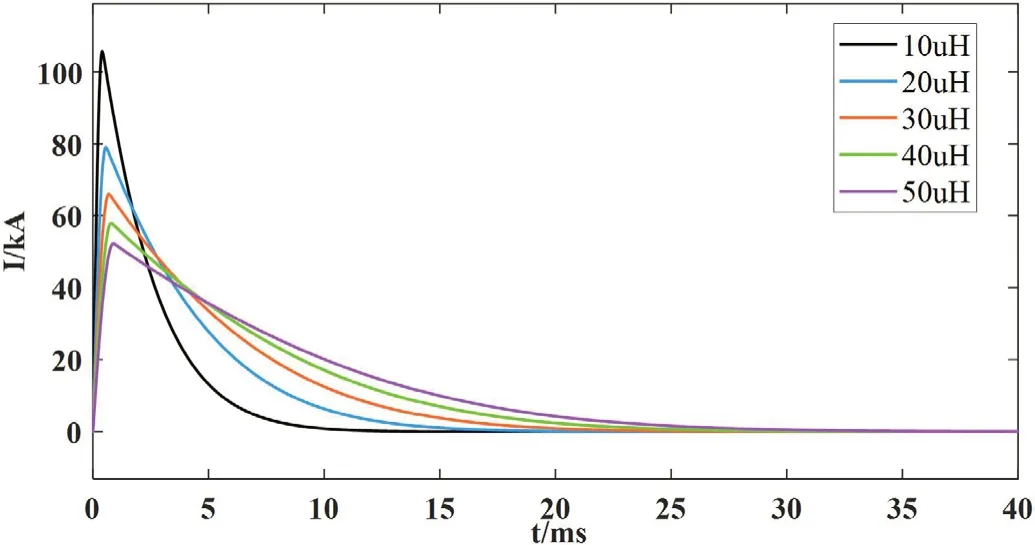
图8：调波电感参数特性

图9：调波电感等效内阻参数特性

3.3 电源模块数及放电时序参数分析

为达到弹丸超高速的发射要求，增加电源模块数并适当选取晶闸管导通时刻可使放电电流达到预期水平。除了获取较大的峰值电流，电磁轨道炮的还应保持理想的加速过程，这要求电流能够在初始时刻迅速达到峰值，在该值附近维持一段时间，待炮弹离开炮管后电流迅速下降，减少能量的损失，即获得近似梯形波的最佳曲线。因此实验通过并联的连接方式，分成相同时序不同数量电源、不同时序电源进行分析。

3.3.1 相同时序多级电源

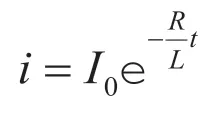
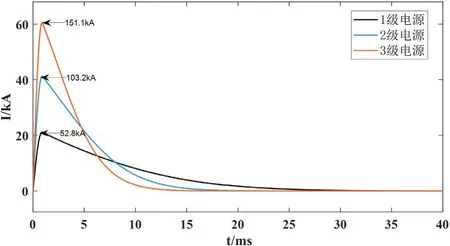
图10：相同时序参数特性

3.3.2 不同时序多级电源

为更好的得到梯形波，仿真使用5组电容器电源。各电源使用默认参数，不同脉冲触发时序见表2。

表2：多级电源3种触发时序

根据上述触发时序得到图11仿真曲线。由于每组的电源编号1均为起始脉冲，因此在0-3 ms图像保持重合。3 ms以后，各组图像出现变化，触发时序为4 ms的组别，最先达到峰值电流，在4.83 ms时峰值电流达到85.33kA；初始触发时序间隔为3 ms、逐渐减小0.5 ms的组别在6.26 ms脉冲电流为最大值103.64kA；触发时序为3 ms达到峰值最晚，为6.75 ms，且电流值97.22 kA介于前两者之间。在下降过程中时序3曲线最陡，最快达到稳定值，结束续流；时序2曲线上下波动，加速过程时间最长，可以明显看到在20 ms电流值远远高于另外两组时序。由此仿真可以得到结论，随着脉冲触发时序的增大，最大电流持续时间也会增加，但峰值电流会逐渐下降，该时刻的快慢与时序具体取值有关。时序3最近似梯形波，该曲线既能在较快速度上升到最大电流，且各组电源达到最大电流差值最小，能够近似维持在合适的取值并扩大脉宽，使弹丸增大出膛速度的同时还减小了对炮管的损伤。因此想要得到最佳梯形波，在保证使用材料等基础前提下，我们可以通过人工智能算法，例如模拟退火算法等将峰值电流和脉宽作为目标函数进行优化，得到最优解。

图11：不同时序参数特性

将两组仿真代表曲线进行对比，得到图12。在时序问题选择上，由于电磁轨道炮理想波形为平顶波，一般采取不同触发时序电源，该方式使炮弹可以在恒定加速度下得到充分的加速，有效的提高了能量利用率；但是相同时序多电源并联发射的优点体现在极短的时间下达到峰值电流，且最大值远超不同时序的情况，这种高成本、低利用率的方式一般适用于大电流、窄脉宽的发射要求。

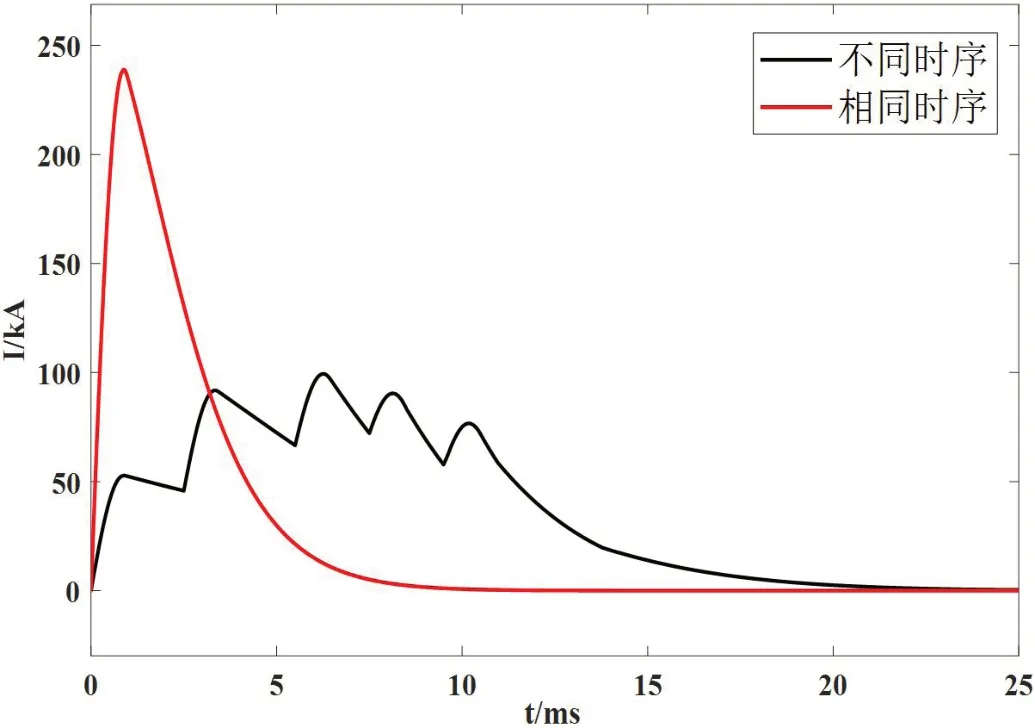
图12：多级电源触发时序比较特性

4 结论

本文以模块化思想和控制变量法为核心，使用Simulink分别搭建脉冲功率电源及电磁炮负载理想化模型，通过调节电源参数，模拟了峰值电流及电流脉宽随时间的变化情况。经多组仿真表明，对于单电源模块的整个电流变化过程，续流过程持续时间远超过电容供电过程，电路结构主要以RL一阶电路存在，所以改变各条件对RLC二阶放电回路周期影响不大。电源预充电压及电容与峰值电流呈正相关，而调波电感的增加会明显降低峰值电流，对电流脉宽起决定性作用的元件为调波电感，该结果符合仿真前的理论分析。对于多级电源，相同时序增加电源级数会明显提高峰值电路并减小脉宽，这对于系统的寿命和弹丸出膛速度均产生不利影响，因此本文通过控制并调节每级电源的时序增量有效延长了电流脉宽，维持峰值电路在理想值，对未来使用人工智能算法得到最优触发时序，继而研发出最优电磁发射用脉冲功率电源提供了思路。