基于星载GNSS数据的低轨卫星精密定轨

武子谦 张京奎

（中国电子科技集团公司第五十四研究所 河北省石家庄市 050081）

1 引言

全球卫星导航系统（Global Navigation Satellite System,GNSS）可以向全球各类用户提供全天时、全天候的定位、导航和授时服务（Positioning，Navigation and Timing,PNT）。目前，美国的GPS 系统、俄罗斯的GLONSS 系统、欧盟的Galileo 系统和我国的北斗卫星导航系统（BDS）均可提供全球范围内的PNT 服务。此外，日本的准天顶卫星系统（Quasi-Zenith Satellite System, QZSS）和印度区域卫星导航系统（Indian Regional Navigational Satellite System,IRNSS）等可为其服务区用户提供PNT 服务。随着GNSS系统的发展与完善，以及星载接收机研制技术的发展，GNSS 系统不仅可以满足地面用户的高精度定位需求，还可以为空间用户提供高精度的轨道信息。

将星载GNSS 接收机安装在不同类型的飞行器上，可以通过接收导航卫星信号进行轨道确定，保障飞行器执行任务。星载GNSS 测量具有成本低、精度高的特点，与其他测量手段进行联合处理时，能够显著提高测量的精度，已经成为飞行器轨道确定的重要测量方法。低轨卫星在科学试验、测绘、通信、遥感等多个领域发挥着至关重要的作用，卫星精密轨道确定是低轨卫星提供各类服务的基本前提。随着我国低轨卫星星座的建设，以及星载GNSS 技术的发展成熟，基于星载GNSS 技术的应用将越来越广泛。

本文阐述了基于星载GNSS 数据的低轨卫星动力学定轨原理，介绍了卫星轨道精度评估方法，并基于实测星载GNSS 观测数据开展精密定轨试验，验证了低轨卫星的定轨精度，为未来低轨星座的精密轨道确定提供参考。

2 动力学精密定轨原理

星载GNSS 定轨技术的原理为，搭载在低轨卫星上的GNSS 接收机接收GNSS 卫星的导航信号（与GNSS 卫星的距离观测量），利用对多颗GNSS 卫星的多历元距离观测量进行动力学定轨，解算飞行器的状态量和动力学模型参数，得到飞行器的位置和速度信息。本节就测量模型、动力学模型和模型线性化三个方面简要介绍低轨卫星动力学精密定轨的原理。

2.1 测量模型

星载GNSS 接收机r 接收到GNSS 卫星s 的伪距、相位观测量描述如下：

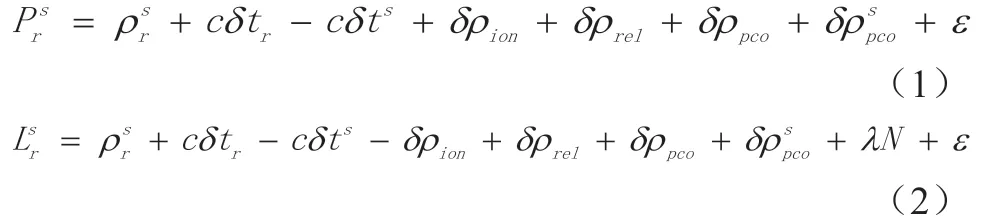
由于中性大气层高度为80 km 以下，而搭载星载GNSS接收机的飞行器轨道高度大都在200 km 以上，因此星载GNSS 接收机不受对流层延迟的影响。此外，与地面的导航接收机相比，星载GNSS 接收机不受测站的固体潮和海潮位移的影响，多路径效应也大大削弱。相比于伪距观测方程，相位观测量所受电离层延迟误差符号与伪距相反，且存在相位整周模糊度参数。星载GNSS 观测值中包含各类误差，因此在进行数据处理前需先将电离层延迟、GNSS 卫星及星载接收机的天线相位中心偏差、相对论延迟、相位缠绕等误差项修正。

在星载GNSS 数据处理中，常常需要利用频率之间的伪距和相位观测值按照不同需要进行线性组合，常见的几种组合方式包括无电离层组合、电离层残差组合、宽巷组合、MW 组合等。本文在开展星载GNSS 定轨时采用无电离层组合观测值。根据电离层误差与频率平方呈反比的规律，无电离层组合能够消除一阶电离层的影响，因此被广泛使用。然而组合后的相位模糊度失去整数特性，且测量噪声会被放大三倍。伪距和相位的无电离层组合观测值可表示为：

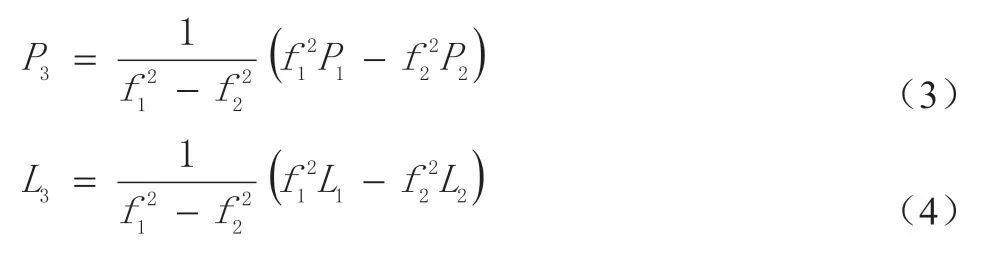
2.2 动力学模型

卫星在惯性系中的运动方程可描述为：

卫星所受的保守力可表示为：

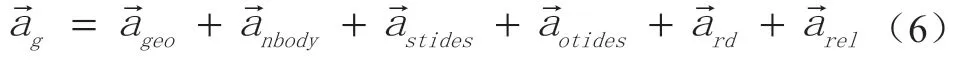
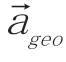
卫星所受的保守力可表示为：

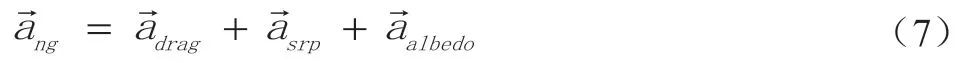
由于卫星所受太阳辐射压摄动模型为经验模型，同时还可能有其他与轨道周期有关且未能精确模制的动力学模型，因此还需要引入经验力模型，用于吸收模型误差。将未能模制的摄动分为轨道径向R、沿迹方向T 和法向N 的周期函数，可以模制成轨道周期、半周期等。

2.3 模型线性化

在卫星精密定轨处理中通常包括两类待估参数：一类是卫星动力学参数，包括卫星初始轨道参数、太阳辐射压参数、经验加速度参数等出现在卫星运动方程中的待估参数；另一类是只出现在观测方程中待估参数，或称为几何参数，如测站坐标，地球自转参数、测站大气天顶延迟以及钟差参数等。

根据前两节，卫星动力学方程和观测方程均非线性方程，为采用最小二乘法则进行参数估计，需对两类方程进行线性化。

设动力学方程可以写为：

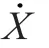
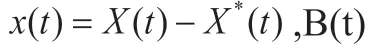
状态量X 通过状态转移矩阵 从t时刻转移到t 时刻，即 是以下矩阵微分方程的解：

设观测方程可写为：

其中Y为第i 个观测量，G(X, t)为t时刻状态量的函数，即观测量理论值计算公式，ε为观测噪声。

对上式线性化后可写为：

在精密定轨待估参数包括：卫星初始轨道参数、太阳辐射压参数、经验加速度参数等出现在卫星运动方程中的待估参数以及钟差参数等。单星精密定轨流程图如图1。

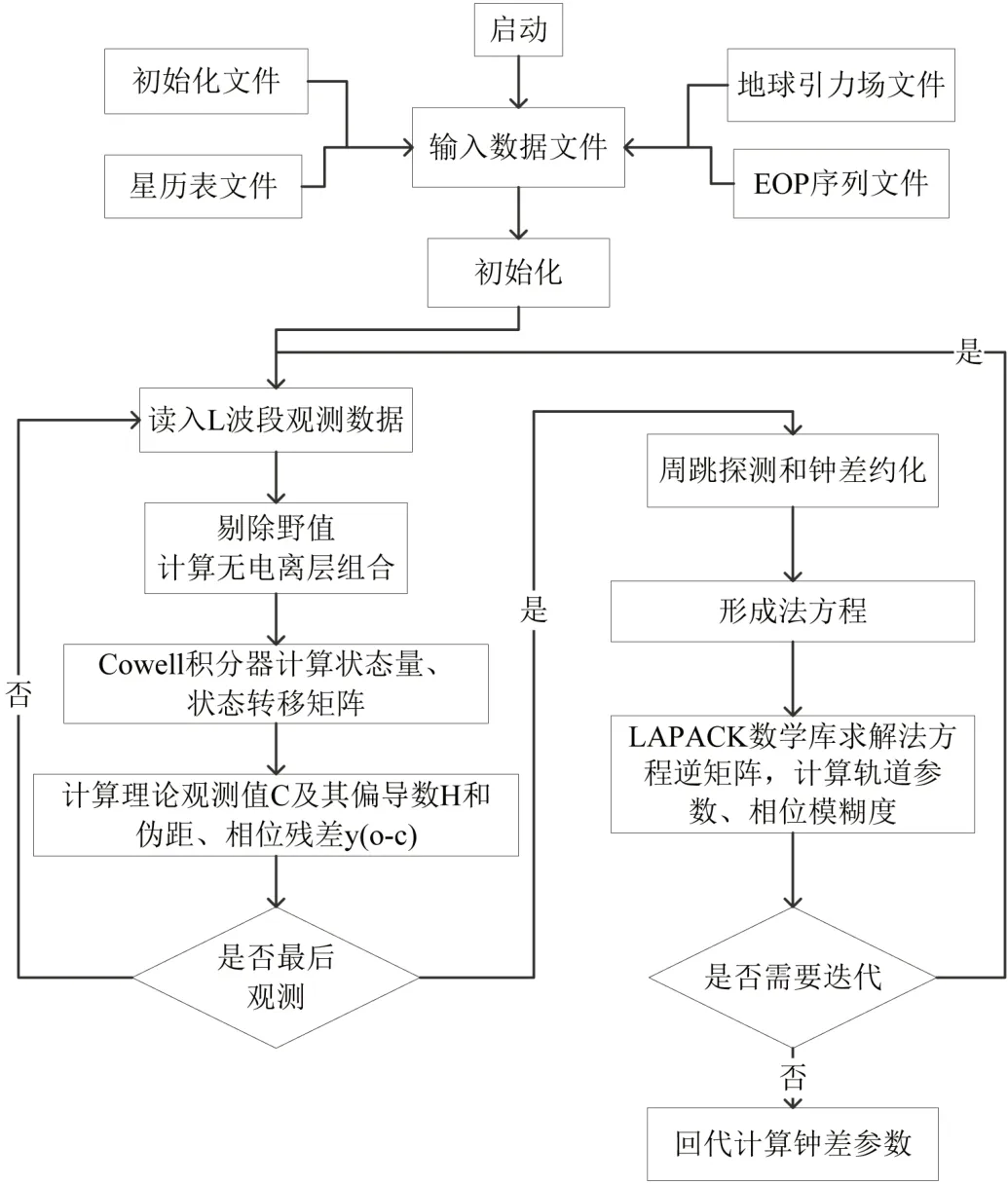
图1 ：动力学精密定轨流程图

3 定轨精度评估方法

常用的定轨精度评估方法包括内符合精度、轨道重叠检验、SLR 校验和独立轨道检核等方法。这四种方法可全面、客观的评价定轨精度，各种轨道精度的评价方法如下。

3.1 内符合精度

内符精度，亦即残差的 RMS，是轨道精度的一个重要的、但不是绝对可靠的标志。一般来说，要判断轨道的精度，首先要观察的就是观测资料的拟合程度。如果观测资料的残差很大（比如说要比观测的宣称精度大一个数量级），则说明计算可能有误。只有当观测资料的拟合达到令人满意的程度，或者说观测资料残差RMS 不能看出明显的计算错误时，才可以用其它的方法来对轨道精度进行评价。但是，不能将观测资料的内符精度当作评定轨道精度的唯一和绝对标准。

3.2 轨道重叠检验

星载 GNSS 定轨常用的定轨弧长为24 小时。对于24 小时的定轨弧长，一般使用3 小时重叠的数据，如图2 所示。尽管这3 小时的观测数据是相同的，但这两段轨道是通过两次独立解算得到的，可以认为这两段3 小时的重叠轨道不相关，因此，轨道重叠部分的符合程度可以反映轨道精度。为减小端部效应的影响，在评估重叠轨道的精度时截除了3小时重叠部分的前30 分钟和后30 分钟数据，只选取中间2小时的数据作为评估轨道精度的有效数据。

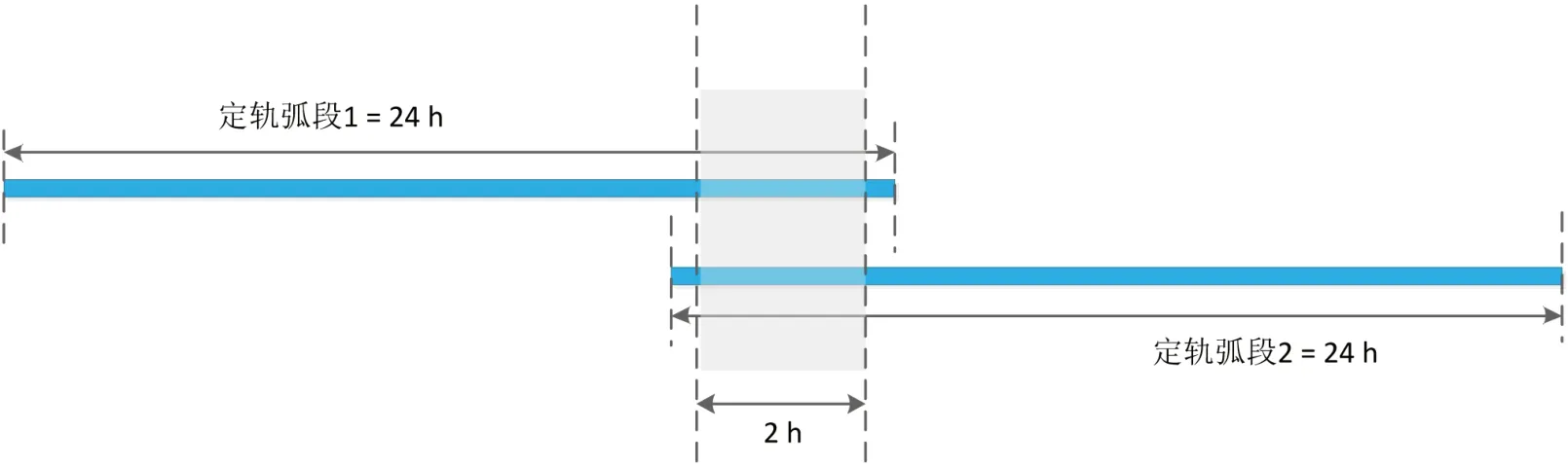
图2 ：轨道重叠弧段示意图

3.3 SLR校验

对于星载 GNSS 定轨，评估其定轨精度的另一重要手段就是利用高精度的激光测距数据对星载GNSS 定轨结果进行外部检验。目前，SLR 观测数据的观测精度可达1cm，且无模糊度也不受电离层的影响，因而，其可用于星载GNSS 定轨结果的检验。检验过程中，SLR 残差为SLR 直接测得的站星距与星载GNSS 定轨结果计算得到的站星距之差。

激光评估轨道精度计算公式如下：

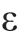
3.4 独立轨道检核

利用外部独立轨道产品与定轨结果进行比较，评估轨道的外符合精度。通常情况下，将定轨结果与不同机构发布的精密轨道产品对比，统计轨道序列差异的RMS 值作为独立轨道检核精度。

4 星载GNSS精密定轨处理实例

GRACE (Gravity Recovery and Climate Experiment) 计划是由美国国家航空航天局（NASA）和德国航空中心（DLR）合作的项目，包括两颗几乎完全一样的卫星GRACE-A 和GRACE-B，主要用于重力场恢复以及大气电离层的探测等。GRACE 于2002年3月发射成功，卫星的设计寿命为5年，超期服役至2017年坠毁。GRACE-A 和GRACE-B 卫星轨道高度约为500 km，双星相距约220 km。每颗GRACE 卫星上搭载了美国喷气推进实验室（JPL）研制的 BlackJack GPS接收机，该星载GPS 接收机具有16 个通道，其中12 个用于卫星的精密轨道确定，4 个通道用于掩星测量获取精密大气层剖面，此外还搭载了微米级测距精度的K 波段测距仪、加速度计和激光反射器等。

本文基于上述介绍的动力学精密定轨方法，使用GRACE-A 卫星2016年1月2日至3日的星载GNSS 观测数据和GPS 精密轨道和钟差产品，对GRACE-A 卫星开展动力学精密定轨处理。GRACE-A 卫星的动力学模型及待估参数如表1 所示。

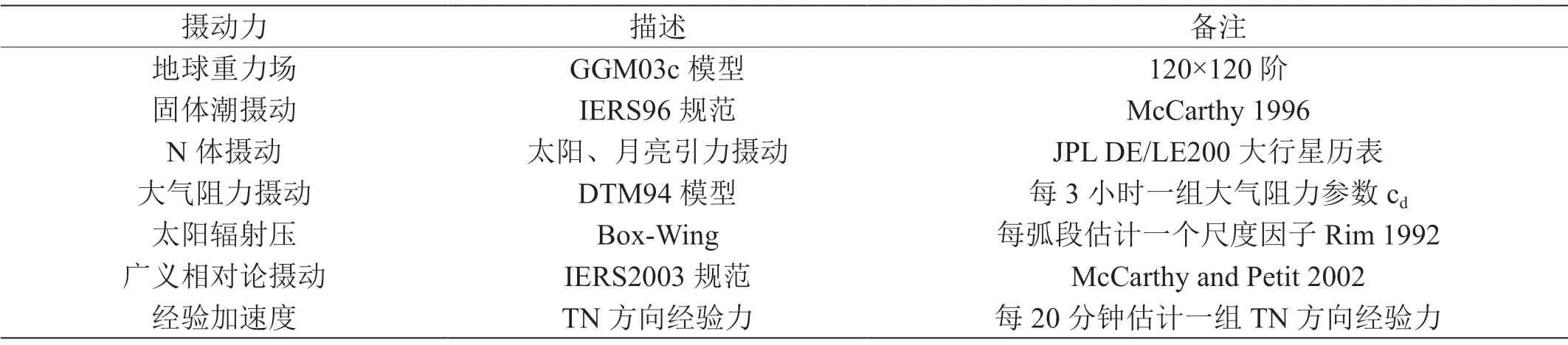
表1 ：GRACE-A 定轨时使用的动力学模型

采用独立轨道检核方法，将定轨结果与JPL 发布的标准轨道进行比较，分析结果表明，基于星载GNSS 的GRACE卫星动力学定轨精度优于4cm，定轨精度序列图和统计结果如图3 和表2 所示。

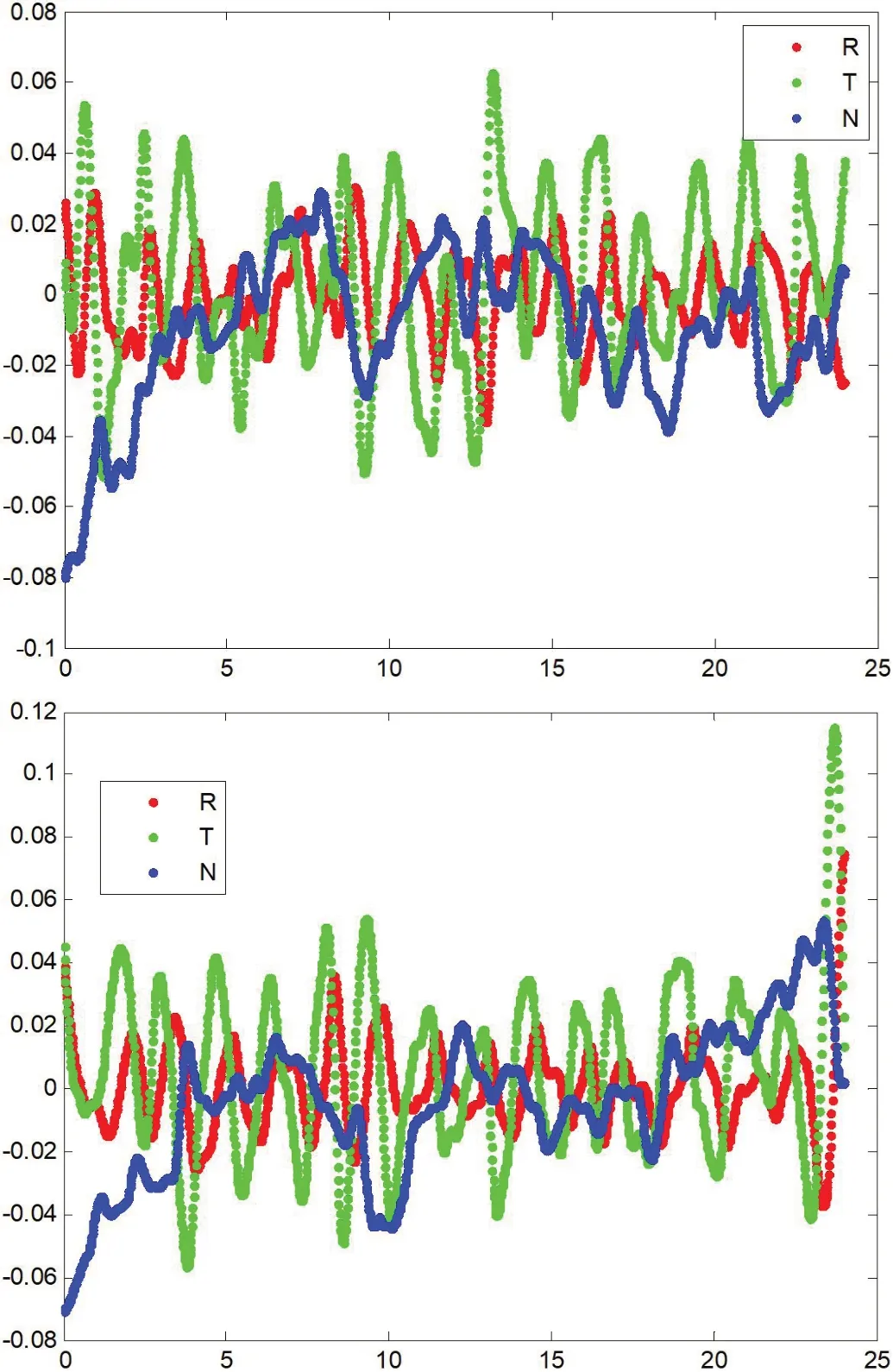
图3 ：GRACE-A 卫星精密定轨精度序列图

表2 ：GRACE-A 动力学定轨精度统计表

5 总结

随着我国低轨卫星星座的建设与发展，低轨卫星将在更多领域发挥重要作用，而卫星精密轨道信息是低轨卫星提供高性能服务的前提。本文介绍了基于星载GNSS 数据的低轨卫星动力学定轨原理，并基于实测星载GNSS 观测数据开展低轨卫星精密定轨试验。分析结果表明，基于星载GNSS 定轨技术可获取厘米级的低轨卫星轨道。星载GNSS 定轨技术具备低成本、高精度的优点，可为未来低轨星座的精密轨道确定提供参考。