基于可拓实例推理与参数化设计的产品特征线演进方法

近年来，工业产品不断推陈出新，人们不再满足于功能优化，对产品外观也提出了更高要求。造型作为产品外观的主要特征，其变化主要是自由曲面的演变，在实际生产中，曲面受加工工艺和制造成本的制约，不能自由变化。在实际造型设计工作中，大都根据“线动成面”原理，即曲面的基本特征通过线的运动实现，特征线决定了产品的主要造型。传统工业产品造型设计工作存在两个问题：（1）依赖设计人员操作，重复劳动，流程烦琐，不利于快速得出方案；（2）依赖设计人员的职业素养，常常不能准确提炼已有的产品造型语言，并进行恰当的应用。对国内医疗设备生产企业进行调研发现，在医用台车产品线的迭代升级设计方面，大多数企业以传统设计方法为主。因此，文章结合遗传算法与可拓学理论，构建参数化的造型特征演化流程，尝试在保留原产品家族设计语言的基础上演化出多种产品造型特征线方案，以供设计人员选择。

在鼻胃镜可通过狭窄病变的病例中，利用鼻胃镜成功辅助完成46例消化道狭窄内镜下治疗，成功率100%。在食管癌中，行16例支架置入/调整术，2例光动力治疗；食管术后吻合口狭窄中，行5例支架置入术，2例吻合口狭窄扩张术，1例引流管置入术，1例光动力治疗术；食管外压性狭窄中，行1例支架置入术；食管不明原因性狭窄中，行1例扩张术。胃癌中，行7例支架置入术，1例肠梗阻导管置入术；胃术后吻合口狭窄中，行2例支架置入术，1例营养管置入术。结直肠癌中，行4例支架置入术，2例肠梗阻导管置入术(表6)。

1 可拓实例推理与参数化设计理论概述

1.1 可拓实例推理

可拓实例推理，是一种建立在可拓学基础上较成熟的产品设计演化方法，是可拓学基元理论及实例推理技术（CBR）相结合的一种应用方法。它的主要思想是基于实例，借助之前的设计知识来解决在当下产品设计中遇到的问题

。依托可拓实例推理进行产品设计的方法，即是可拓设计。实例检索作为实例推理的核心，其目的就是找到与需求最为相似的实例。国内外许多学者对该方法开展了深入的理论及应用研究，在机械设计、建筑设计、工程施工组织产品设计等多个领域形成了很多有积极影响的学术成果。例如，浙江工业大学的赵燕伟教授、苏楠等人提出了产品信息物元匹配的实例检索方法，并将其应用于产品的进化设计和产品家族设计系统，完善了可拓实例推理在产品设计方面的应用

。

1.2 参数化设计理论

在计算机辅助工业设计技术（CAD）普及之前，曲线线条一般需要设计人员借助尺规等绘图工具手绘，不规则的自由曲线需要设计人员徒手绘制样条，尺寸不规范、不便缩放等因素导致实际生产可行性较差。随着技术的不断发展，现代工业产品的造型更加趋向于多元化，自由曲线在产品造型设计上的运用也越来越广泛

。

现代产品造型自由曲线的基础之一是NURBS 曲线（Non-Uniform Rational B-Spline 非均匀有理B 样条曲线）。NURBS 曲线的定义如下：由节点矢量

={

，

，

，…，

u

}，控制点矢量

={

，

，…，

P

}，权值矢量

={

，

，…，

w

}决定的

次NURBS 曲线

可表示为：

在进行企业各机构的预算管理工作时，应该严格按照市场经济的发展趋势进行企业体制改革，尤其是在预算管理方面。具体而言，可以在管理中推行《企业财务预算管理制度》，在制度的执行过程中，无论是财务管理者还是预算执行者，均需要对已经统一编制完成的预算管理原则以及相应的编制依据了若指掌，唯有如此，才能更好的将企业的预算管理情况与实际收支状况相整合出来，最终交由企业预算管理部门进行综合处理。另一方面，为了保障企业预算管理中不会出现赤字情况，还需要就日常的预算进行实时统计分析，借以提升资金运行效率，确保企业收支平衡。

NURBS 曲线的定义说明，特征线的特征主要由控制点体现，即特征曲线的形态可以通过点来控制，将多样的数据转换成统一的数据形态，进而通过与参数相关的算法进行处理。例如，燕山大学的黄紫双等人研究了二次曲面的NURBS 拟合方法，构建了基于分数傅里叶变换的曲面重构算法，并获得最优重构曲面

。武汉大学的张驰、杨雪松等人提出了基于遗传算法的地形道路NURBS 曲线生成模型，应用于旅游风景区的道路路径规划

。

当点在区间中点时，该点最符合要求；<

，

>可以是开区间、闭区间、半开区间

。

2 基于可拓实例推理与参数化设计的产品造型特征线演进流程

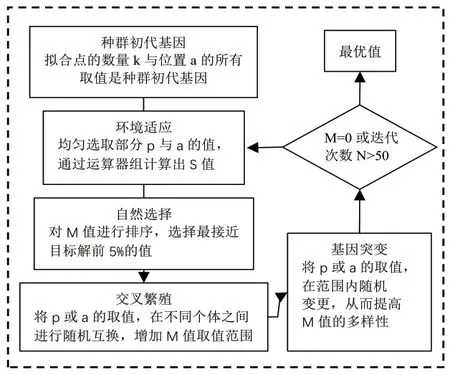
基于Grasshopper 平台，使用Galapagos 运算器，可以方便地应用遗传算法进行曲线特征的拟合。在Galapagos 遗传算法的运算中，每次迭代通过一个适应度函数来对种群进行筛选，适应度是种群中的个体对最优解的贡献度。交叉操作和变异操作是两个关键。交叉操作实现了随机交换信息，以产生新的组合；变异操作可使算法过程不会过早收敛到局部区间，以至于产生无法进化的单一群体，增加了全局优化的特质。随着Galapagos 运算器中遗传算法结果的不断迭代变化，控制点数值随之不断变化，目标特征曲线也随之发生变动，最后得到迭代结果下产品的大致造型。

2.1 特征曲线的提取

为了塑造企业产品线的设计语言，增强设计风格的传承性，新产品的造型特征往往源自同类产品或由原型号迭代而来。从现有产品出发，进行特征曲线的提取与整合是新产品造型研究的重要步骤。在实践中，产品的型号往往繁多庞杂，特征曲线的提取应由设计人员完成。首先梳理产品线，建立产品库，然后提取特征曲线，由此建立造型特征库，为下一步工作做好准备。

2.2 特征曲线的参数化

特征曲线的演进，需要对曲线实现矢量化控制。基于Grasshopper 平台，可以将产品特征曲线转化为NURBS 曲线并进行参数化控制。Rhinoceros 是工业设计常用的一款3D 造型软件，Grasshopper 是一款基于此软件的可视化编程插件平台，在Rhinoceros 的基础上提供了基于各类数学模型和算法的运算器，弥补了Rhinoceros 在参数化方面的不足

，Grasshopper 也支持Python 语言以满足设计人员更复杂的需求

。

采用距离法对曲线特征库进行实例推理可方便地计算出需求特征与实例库中特征之间的相似程度。可拓距离可以量化描述曲线的差异，以定量的形式，精确描述点与区间的位置关系，一般情况下，通过欧氏距离函数来计算各个控制点取值的差异以判断曲线的相似度。但曲线的控制点在空间内是自由移动的，使用欧式距离无法比较其取值差异。为了描述事物（区间内的点）的区别，在可拓学中规定：实轴上任意一点

与区间

=<

，

>之距为：

通过可拓实例推理得到了已有产品线的设计语言，新产品的设计风格还需要融合用户意向。从可拓实例推理得到的特征线上随机提取

个点，将这些点的位置记作

，使用多段线依次连接

个点，生成拟合特征线。定义拟合特征线与用户意向特征线的相似程度为M，随着

值和

值的改变而改变。在拟合特征线上均匀地取点记作

，计算点

到用户意向特征线的最小距离L，累加并除以

的值，所得

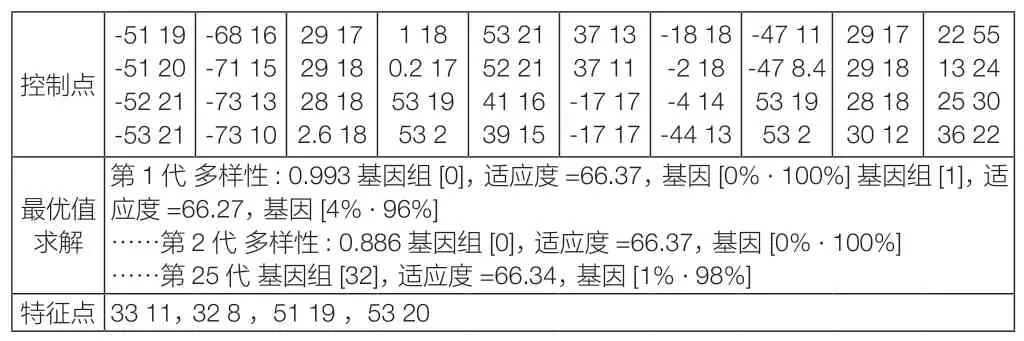
值越小，相似程度越高。拟合目标在满足上文可拓推理结果的前提下，使拟合特征线与用户意向特征线的相似程度达到最高。基于遗传算法拟合特征线与用户意向特征线的原理，如图2 所示，根据该原理连接运算器组。对Galapagos 运算器的参数进行设置，优化初始父代个体数量、繁殖代数及新一代中父代数量的保留率等参数以提升遗传算法的优化精度。Galapagos 运算器得到的结果，如表3 所示。

2.3 曲线特征的可拓实例推理

Solidworks、Creo 等参数化软件，在CBR 领域也有一些探索

，然而这类造型软件虽然在产品打样、投产阶段具有精度优势，但也限制了其造型能力，严谨的尺寸标注和装配体系使其几乎不具备容错性，而在涉及优化算法等非精确性计算过程的研究中，一个具备容错性的平台是十分必要的

。

区间的相似度计算：不论两区间

、

何种关系，可以将区间相似度式定义为：

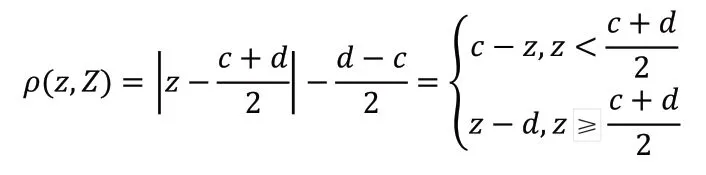
参数化设计中的遗传算法（Genetic Algorithm）工具是一类重要的全局数学优化算法，基于自然进化中的适应性原理，起源于达尔文的生物进化论及孟德尔的群体遗传理论，主要通过模拟自然界的遗传进化机制，优化搜索最优解

。

综上，确定虾油、味精、食盐、白砂糖、干贝素、焦糖色、酵母抽提物和变性淀粉为本产品开发的主要因素，将这8个因素分别设定几个水平，建立L18(2×37)正交表进行实验，以确定最优配方[5]，因素水平见表1。

基于区间的实例相似度计算，可以判断多个已有实例曲线之间的相似性并进行整合。

存在价值是衡量一件物品的主要标准，针对非物质文化遗产，应当主动结合其文化价值与使用价值两方面，如此才能体现及具备一定的市场受众和突出其自身的市场价值。

2.4 曲线特征的拟合

从理论出发，梳理产品造型特征线的演进流程，结合可拓学理论与参数化设计思想，搭建流程框架，如图1 所示。涉及的主要理论工具有可拓实例推理理论、Grasshopper 参数化设计及Galapagos 遗传算法工具。

3 基于可拓实例推理与参数化设计的产品造型特征线演进实践

根据上述流程，进行基于可拓实例推理与参数化的产品造型特征线演进实践，针对A 公司的一款产品，逐步推进设计需求挖掘、已有产品特征库建立、特征提取、用户意向提取、特征拟合、建立方案模型等工作，验证设计流程的可行性。

3.1 设计需求

A 公司是医疗设备领域的主要企业之一，在竞争激烈的市场环境中，A 公司为扩大企业的知名度，提高了自身的品牌价值，实现产业的快速升级，亟需梳理整合已有产品线，提升产品设计语言的统一性和传承性。在医用台车产品方面，亟需扩充产品线，构建产品族，来满足不同场景下的设备承载需要。

以某型医用台车外观升级换代为契机，基于现有产品线风格特征创造多种新的产品造型。以机头造型设计为例，应用参数化特征设计理论，提高设计工作的效率，并形成设计流程供其他医疗设备参考。

那一年，我中途接手了一个班，第一课上的是《草原》。这是语言大师老舍先生的一篇散文，语言简洁，感情真挚，意蕴深刻。我先为孩子们进行示范朗读。

3.2 已有产品特征库的建立

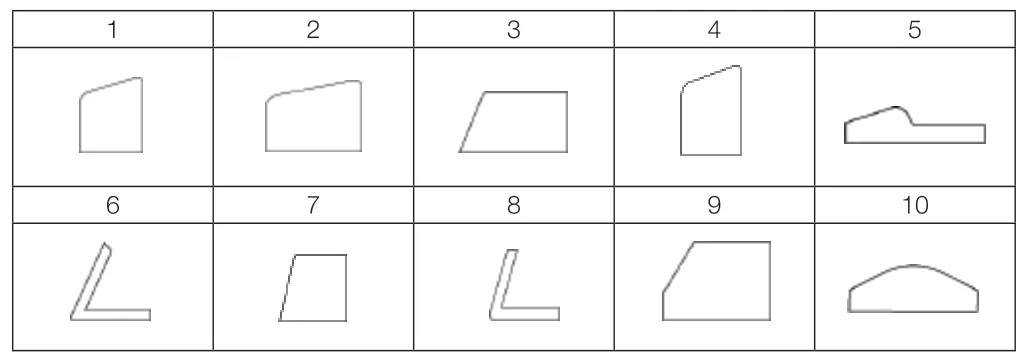
将已有台车类产品的造型设计特征库作为特征参数化演进的基础，对其外观进行统一处理，提取造型特征。医用台车造型特征线主要可以分为正面轮廓线和侧面轮廓线，以医用台车的侧面机头特征线为例进行阐述。

在A 公司的现有台车类产品库中，选取销量最大，应用最广泛的10 款代表性产品。搜集其侧面图片，如表1 所示。

使用illustrator 软件对10 款产品的侧面轮廓线进行处理，忽略造型细节，针对产品的主要造型风格特征，勾勒出特征线，如表2 所示。

3.3 基于可拓实例推理的特征提取

设结果区间为

，取点

，

…

M

，已知实例特征曲线A，顺序取点

，

，…

A

，已知实例特征曲线

，取点

，

，…，

B

。设所求主要特征点为（

，

），（

，

），…，（

x

，

y

），令

=4，分别表示特征点与已知主要特征点的相似度函数。在Grasshopper 中，利用Text Panel 运算器导入已知特征点，分解为坐标值，运用Evaluate 运算器输入可拓距相似度计算函数。根据产品属性、造型特征线的可行区间端点值进行分解，构成二维平面上的4 个点。过点

和点

作两条坐标轴的平行线可构成一个二维封闭空间

，过点

和点

作两条坐标轴的平行线也可构成一个二维封闭空间

，且

∈

。对实例推理结果进行分析，观察相似度分布情况，得到特征库中相似度最大的特征线。使用问卷法调研产品用户，构建模糊评价矩阵，获取每个准则层的元素评价等级，依据各元素的评价等级及评价次数，得出评价矩阵结果，选定产品6 提取为用户意向特征线。

3.4 基于Galapagos 的特征拟合

利用Grasshopper 平台的参数化能力，对造型特征曲线进行参数化表示，然后借助算法，对特征曲线的控制点进行变化

。基于Point 运算器，可以获取控制点的向量和顺序数据，基于Nurbs Curve 运算器，可以生成控制点曲线。

从南糯山下来，进到景洪市区时，天已彻底暗下来。这时我才发现，几乎整个景洪城的人，都在喝茶。每家店都水汽弥漫，茶香飘逸，你只要吸吸鼻子，就能闻到西双版纳的味道。

3.5 方案模型

根据得到的方案特征线，在Grasshopper 中建立参数化草图并进行烘培操作，得到草图模型后，参考以往产品造型，补全产品的外在部件特征，优化细节，最终在Rhinoceros 中建立三维模型，如图3 所示，建立医用台车方案模型。

4 结语

依托Rhinoceros 软件，创新性地建立以Grasshopper 插件为造型特征线参数化平台，以可拓学理论为特征线实例推理手段，以基于遗传算法的Galapagos 插件为优化求解工具的特征线演化流程。通过参数化、自动化的方式推演主要造型特征，保证了设计结果的可靠性和一致性。将特征线参数化推演方法应用于具有多条造型特征线的产品造型设计时，需要综合考虑各特征线之间的联系，进行多次演化，后续的研究中将据此优化设计流程，给予其更好的适应性。

[1]陈尉刚.面向可拓实例推理的产品设计演化方法[D].杭州：浙江工业大学，2015.

[2]赵燕伟.机械产品可拓概念设计研究[J].中国工程科学，2001（05）：67-71.

[3]罗仕鉴，边泽，张宇飞，等.基于形态匹配的产品仿生设计融合[J].计算机集成制造系统，2020，26（10）：2633-2641.

[4]黄紫双.基于NURBS 的曲面拟合和优化方法研究[D].秦皇岛：燕山大学，2020.

[5]张驰，杨雪松.基于Rhino+Grasshopper 的风景环境复杂地形道路选线设计算法模型研究[J].中国园林，2021，37（03）：77-82.

[6]边霞，米良.遗传算法理论及其应用研究进展[J].计算机应用研究，2010，27（07）：2425-2429+2434.

[7]李羿璇.基于Grasshopper 插件的参数化灯具设计[D].桂林：广西师范大学，2018.

[8]唐一伦，许蓁，陈译民，等.曲面生形的传统方法再认知与结构逻辑解读—以Grasshopper 平台下的Kangaroo 插件生形为例[C]//数字技术·建筑全生命周期—2018 年全国建筑院系建筑数字技术教学与研究学术研讨会论文集.2018：138-146.

[9]王冬梅，殷国富，成尔京，等.Solidworks 环境下基于CBR 的机构创新设计[J].现代制造工程，2004（02）：105-107.

[10]Yuan Tao Sun,Ling Dong Zhang,Xian Rong Qin.The Development and Application of Grab Design System Based on Solidworks and CBR[J].Advanced Materials Research,2014,3227(945-949).

[11]张慎，尹鹏飞.基于Rhino+Grasshopper 的异形曲面结构参数化建模研究[J].土木建筑工程信息技术，2015，7（05）：102-106.

[12]赵燕伟，朱芬，桂方志，等.基于可拓距的改进k-means 聚类算法[J].智能系统学报，2020，15（02）：344-351.