小型液氢储罐无损储存影响规律研究

沈铣 滕俊华 周伟明

(1 上海市气体工业协会 上海 200030)

(2 全国锅炉压力容器标准化技术委员会低温容器分技术委员会 上海 200030)

1 引言

氢能作为一种清洁高效,来源广泛的可再生能源,有效克服解决可再生能源空间分布不均和负荷消纳的难题,成为全球各主要经济体能源结构转型的重要选择。但是,由于氢工质燃烧下限低,燃烧范围大,具有易燃易爆的特点,如何实现氢能的高效安全储存是氢能大规模应用的基础前提。

氢能的储存技术有高压储存、低温液化储存、化合物储存和物理吸附储存等。其中,低温液化储存作为最经济的储存方式之一,具有单位体积能量密度高,占地面积小、灵活性强等特点,使其在氢能的储运上具备极大潜力。与常温储存不同,低温液化储存由于沸点较低,环境与罐内低温液体存在较大温差(对于液氢约270 K),热量从环境通过绝热结构流向罐内流体,同时由于低温液体汽化潜热小,易引起储罐内低温液体蒸发,进而导致储罐内压力上升,压力的不断上升可能导致储罐出现超压排放,涨罐等安全事故[1]。相关研究表明,液氢储罐的漏热蒸发损失与储罐的容积比表面积成正比。而球形储罐具有最小的容积比表面积,同时具有机械强度高、应力分布均匀等优点,因此球形储罐是较为理想的固定式液氢储罐[2]。但大型固定式球形储罐生产制造难度大,成本昂贵,因此小型球形储罐有望成为液氢储存装备推广至民用领域的重要选择之一。

由于现有研制的固定式液氢储罐多为圆柱型储罐,针对小型球型储罐储存规律的实验与理论研究有限。20 世纪90 年代,美国宇航局(National Aeronautics and Space Administration,NASA)在格林研究中心(Glenn Research Center,GRC)开展的K-site 储罐系列实验[3-4]是现有公开的小型液氢球形储罐中较为详细完整的实验之一,实验测试了不同操作参数下储罐内部压力、测点温度随时间的变化,为理论研究提供了坚实基础。由于缺少液氢的实验数据,现有理论研究大多依靠基于不同假设的热力模型开展。常见的热力模型有饱和均质模型[5],俄罗斯模型[6],分区模型[7-8],边界层模型[9]和CFD 模型[10]等。考虑到小型液氢球罐体积较小,内部气液相温度较为均匀,本文将基于饱和均质模型和俄罗斯模型,结合相关实验数据,以K-site 储罐为研究对象,研究不同操作参数下小型液氢储罐的储存规律。

2 K-site 液氢储罐的数学模型

2.1 K-site 液氢储罐的几何结构

K-site 储罐结构实物图与示意图[3-4]如图1a 和图1b 所示,从图中可以看出,K-site 储罐截面是一个长轴为2.2 m,长短轴之比为1.2 的椭圆。储罐的容积为4.89 m3,平均壁厚为2.08 mm,在内壁外侧包裹多层绝热(Multi-layer insulation,MLI)材料。

图1 NASA GRC K-site 液氢储罐Fig.1 NASA GRC K-site tank

2.2 K-site 液氢储罐的理论模型

饱和均质模型作为最为理想的一种描述低温流体储存热力行为的理论模型,图2 为饱和均质模型的示意图。该模型假设低温流体的气液相在环境漏热的输入下时刻处于饱和状态,在计算LNG 罐式集装箱的增压上获得了较好的效果[11]。与LNG 不同的是,液氢内部存在两种形态的氢,即正氢和仲氢。室温下的氢被称为正常氢,内部含有75% 的正氢和25%的仲氢,由于氢的正-仲转换反应是自发进行的放热反应,因此当该反应结束后的氢被称为平衡氢。平衡氢中的仲氢含量在0.1 MPa,20.3 K 下达到了99%以上,因此可以用仲氢的物性来代替此时的平衡氢的物性进行计算。

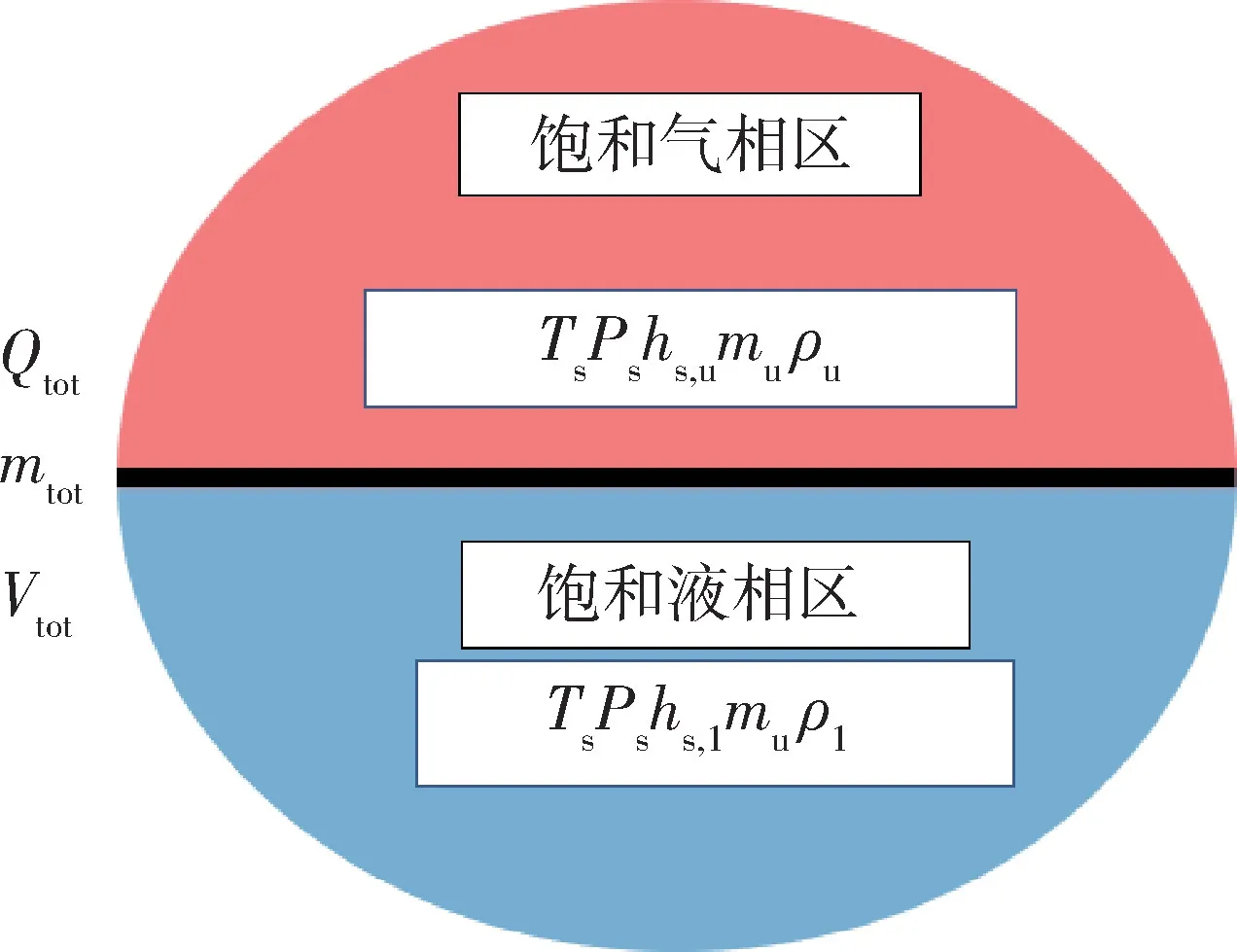
图2 饱和均质模型示意图Fig.2 Thermodynamic equilibrium model

在饱和均质模型中,当储罐内部压力未达到安全阈值且充满率未达到规定充满率的情况下,气液相的质量守恒方程、体积守恒方程和能量守恒方程分别如式(1)—(3)所示。

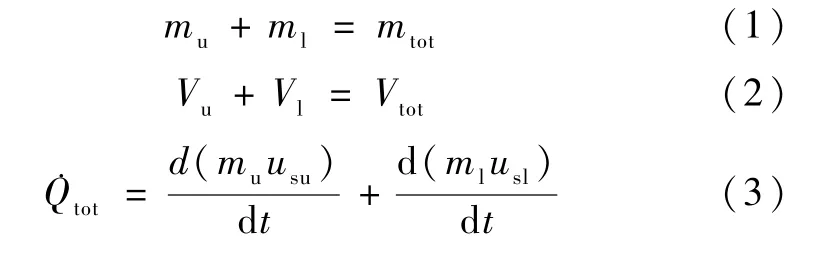
式中:下标u 和l 分别表示储罐内流体的气相和液相,tot 表示总值;m为流体质量,kg;V为流体体积,m3;为从环境进入液氢储罐的漏热,W;usu和usl分别为饱和气相和液相的比内能,J/kg;t为时间,s。

根据式(1)和式(2)可得出储罐内气液相平均比体积vx是一个定值,如式(4)所示:

式中:α0为储罐的初始充满率,定义为初始充装状态下液相体积占内罐容积的百分数;vu0和vl0分别为初始时刻储罐内气液相的比体积,m3/kg;x0为储罐内初始的干度,定义为气相质量占总质量的比例。

因此,从式(4)中可得,储罐内气液相平均比体积和储罐内初始干度及充满率是一一对应的关系。

图3 给出了仲氢在0.1—1.2 MPa 内,不同等干度线下的Ts-vx图,从图中可以看出,液氢无损储存过程在图中沿着某条确定的等比体积线从低饱和温度一直延伸至末态的饱和温度。根据不同的初始气液平均比体积,将不同的初始充满率对应的增压过程分成了3 类工况,分别是:蒸发过程、冷凝过程和涨罐。蒸发过程和冷凝过程分别指的是储罐内氢工质的干度随饱和温度的升高而上升或下降的过程。蒸发-冷凝曲线是划分氢工质在储存过程中蒸发和冷凝两个过程作用区域的临界曲线,其方程表达如式(5)所示。

图3 仲氢的Ts-vx 图(p=0.1—1.2 MPa)Fig.3 Ts-vx diagram of Para-hydrogen(saturated pressure 0.1-1.2 MPa)

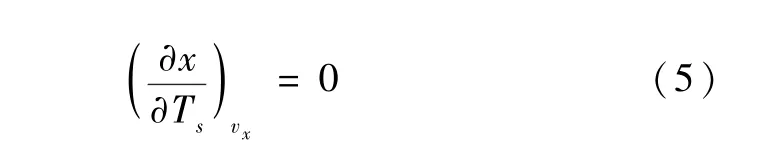
相比于图中的蒸发和冷凝过程,涨罐是液氢储存过程中一个极其危险的工况。涨罐在图中的情况是在储存中达到干度为0 的等干度线(饱和线),即储存末态罐内全是液相。此时当漏热持续输入后,罐内液体受热急剧膨胀对内罐壁施压,一旦超过罐体承受压力将引发液氢储罐泄放、内漏等一系列安全事故。因此在法规与标准中均规定了深冷介质容器在初始充装下非易爆介质充满率不大于95%,易爆介质的充满率不大于90% 的相关规定,而且在储运过程中任何情况下不得超过95%[12]。

饱和均质的假设是理想化的,在实际情况中,液氢储罐内部靠近壁面的部分流体由于壁面过热度的存在而形成了温度边界层,在液相区甚至还在边界层中产生局部蒸发过程。由于浮升力的作用,边界层不断发展和上升,最终在储罐顶部至气液界面形成稳定的温度梯度,即热分层现象。因此,俄罗斯学者通过对不同初始充满率、漏热、体积的液氧、液氮和液氩等低温储罐内部的压力演化数据的研究后,提出了一个适用于预测低温储罐内部压力随时间上升的无因次准则式,该模型用于修正饱和均质模型的计算结果,被命名为俄罗斯模型,其数学表达式如式(6) 所示[6]。

俄罗斯模型是基于不同工质的增压实验总结得到的经验模型,该模型能够用于初始压力为0.1 MPa,初始充满率在0.2—0.9,漏热在5—20 W/m2范围内的球形低温容器的压力演化模拟[6]。

2.3 模型验证

参考文献[3 -4]中K-site 储罐系列实验的相关数据,表1 给出了K-site 储罐系列实验的4 种工况条件,在4 种工况中,漏热的热流密度范围为2—3.5 W/m2,若将K-site 储罐视作理想椭球体,折算的最大漏热量为47.4 W。以液氮介质作为静态蒸发率测试条件,储罐初始充满率为75%折算,表1 所示4 种工况在漏热为47.4 W 下的最大静态蒸发率为2%/d。该数据与现有体积低于5 m3的低温储罐测试的静态蒸发率指标相近,因此表1 所示的4 种工况对小型低温液氢储罐的设计具有代表性。使用饱和均质模型对表1 所示的4 种工况进行模拟计算,结果如图4 所示。

表1 K-site 储罐实验工况条件Table 1 Experimental conditions of K-site tank

图4 饱和均质模型对k-site 储罐4 种自增压实验工况的模拟结果Fig.4 Simulation results from thermal homogeneous saturated model on all experimental conditions of K-site tank

从图4 可以看出,对于体积为4.89 m3的K-site储罐,在4 种工况下饱和均质模型预测的增压速率均小于实验值。这说明对于小体积的液氢储罐,饱和均质模型并不能较好地完成对液氢储存的增压过程的预测和计算,计算结果需要得到修正,图5 给出了俄罗斯模型对4 种工况的计算结果。从图5 中可以看出,尽管俄罗斯模型对增压的预测结果相比实验值还存在一些差距,但其修正了饱和均质模型在增压中后期预测的增压速率偏小的问题,即俄罗斯模型预测的压力变化的斜率与实验测量值的斜率较为一致,这说明了俄罗斯模型预测增压速率的合理性。同时,考虑到现有低温储罐压力表的测量精度在±5 kPa 左右,俄罗斯模型预测结果与实验的偏差可被接受,因此俄罗斯模型对小型液氢储罐内部增压过程的预测计算具备一定的可信度。

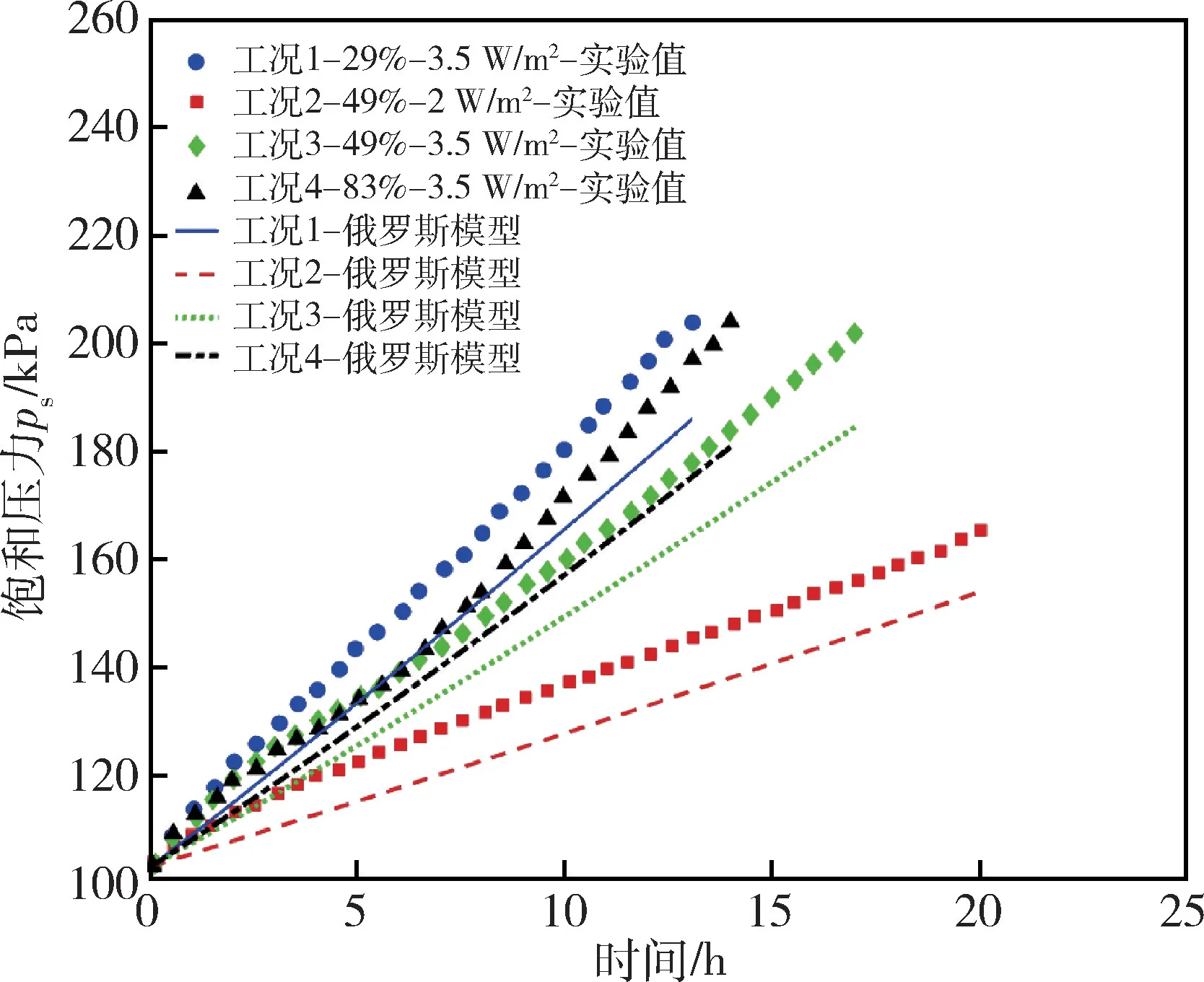
图5 俄罗斯模型对k-site 储罐4 种自增压实验工况的模拟结果Fig.5 Simulation results from Russian empirical model on all experimental conditions of K-site tank

3 维持时间的影响规律

对于小型液氢储罐,在较短的储存时间内,其漏热量可以认为不随时间变化。储罐维持时间的限定条件有两个:(1)储罐压力达到泄放压力;(2)储罐充满率达到95%,当储罐满足两个条件中的任意一个,即认为得到维持时间。对于给定绝热设计和尺寸的液氢储罐,其初始充装状态一定程度上决定了维持时间的长短。以LNG 罐式集装箱为例,在漏热和排放压力不变的情况下,不同初始充满率下的各维持时间存在一个最大值,维持时间最大值对应下的初始充满率也被称为最优初始充满率,经过相关计算LNG 罐式集装箱的最优初始充满率约为84%[11]。由于氢工质与LNG 物性上的巨大差异,这里对小型液氢球罐的最优初始充满率进行模拟计算与影响规律分析。

3.1 漏热条件的影响

液氢储罐由于氢工质的低沸点与小潜热的特性,相比于LNG 和液氮介质,环境热量更易进入罐体引起增压与罐内液体的蒸发损失。漏热条件与绝热结构密切相关,工程经验表明,小型低温储罐的绝热水平对应的静态蒸发率约为中型和大型低温储罐的2—3 倍。这是由于漏热量与表面积相关,储罐体积越小,相应的比表面积越大,因而相应的静态蒸发率越大。结合式(3)和(6)分析可得,对于确定尺寸的储罐,漏热条件的增加将改变不同初始充满率下对应的维持时间。针对K-site 小型液氢储罐,在其他操作参数确定的情况下(初始充压为0.1 MPa,泄压阀压力为0.8 MPa,储存过程中最大充满率不超过95%),使用俄罗斯模型后不同漏热条件下维持时间的计算结果如图6 所示。

从图6 中可以看出,对于给定的漏热条件,维持时间随初始充满率的增大呈现先增加后减小的趋势,在初始充满率为0.55 时达到最大的维持时间。同时,漏热条件对最佳初始充满率的影响几乎没有影响,漏热热流密度从1 W/m2到8 W/m2变化时,最佳初始充满率仍为0.55。不同漏热条件下维持时间与初始和终止充满率之间的关系如图7 所示。

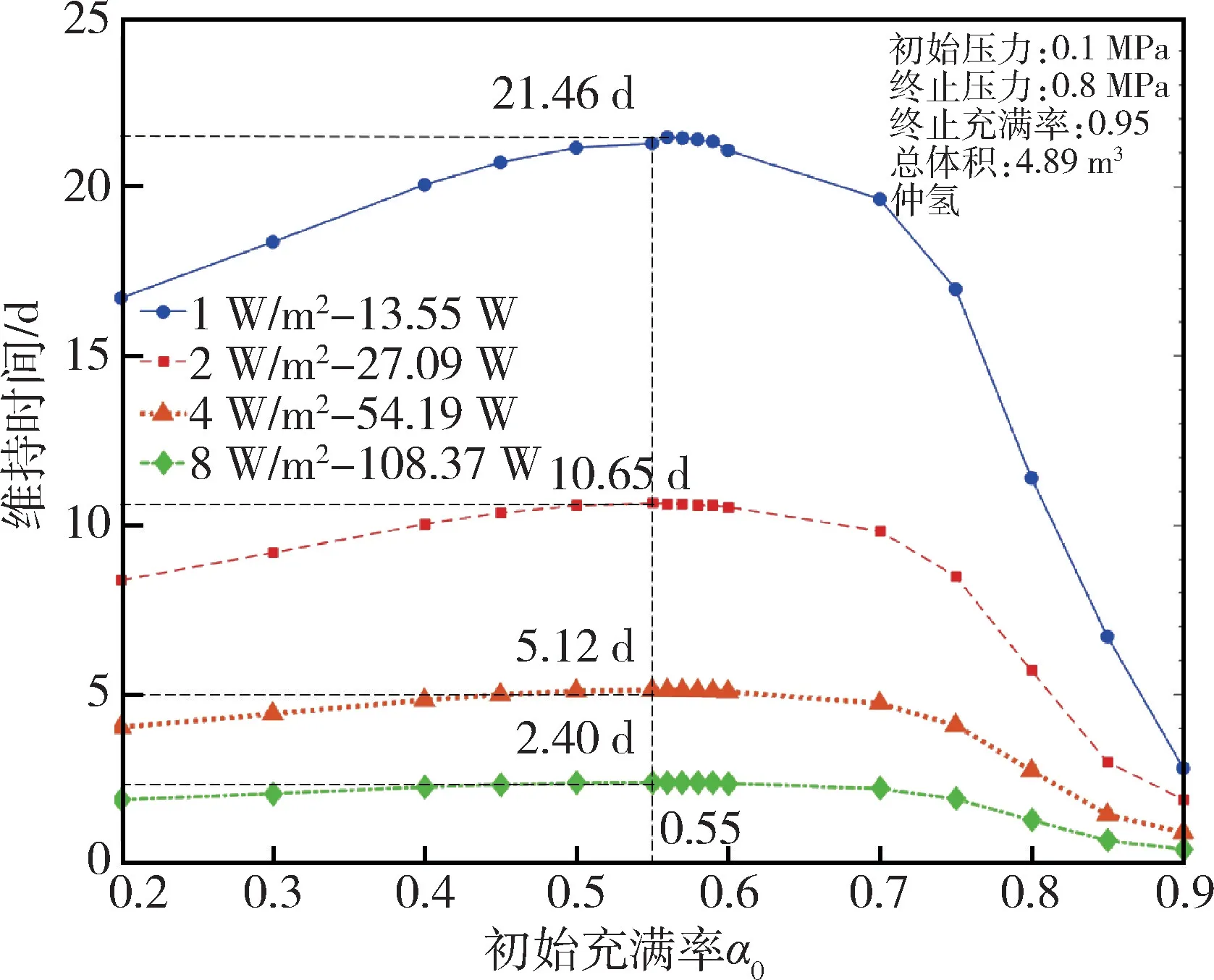
图6 不同漏热条件下维持时间与初始充满率的关系Fig.6 Relationship between storage time and initial filling rate on different heat leakage conditions

图7 不同漏热条件下维持时间、初始充满率和终止充满率之间的关系Fig.7 Relationship between storage time,initial filling rate and terminated filling rate on different heat leakage conditions

从图7 中可以看出,当初始充满率小于0.74 时,对应的储罐终止充满率均小于0.95,这表明此时末态储存时储罐内压力已达到0.8 MPa;而当初始充满率大于0.74 后,对应储罐的终止充满率始终为0.95,这表明此时储存末态储罐内充满率已达到临界值。因此,上述结果表明,在俄罗斯模型预测的结果中,当初始充满率为0.74 即为储存条件的临界值,但并不为最佳初始充满率。

3.2 终止条件的影响

液氢储罐储存的终止条件为储罐内压力达到终止压力ps或罐内充满率达到终止充满率as,两者满足其一就表示无损储存过程的终止。终止压力ps往往体现为泄放装置的整定压力,是由液氢储罐本身的材料及结构强度所决定的。终止压力越高,意味着对罐体材料和结构强度的要求越高。罐内的终止充满率as指标的要求来源于当储罐内液体充满罐体后,液体本身不可压缩性导致罐体在漏热进入后液体迅速膨胀(即“涨罐”现象)而对罐壁产生极大的应力可能使得罐体出现形变、破损甚至爆裂等安全事故的发生。

图8 给出了当漏热为1 W/m2时储罐内压力随时间的变化曲线。

图8 纯仲氢罐内不同阶段的增压曲线Fig.8 Pressure build-up curve on different stages for para-hydrogen

从图8 中可以看出,对于给定漏热条件下液氢储罐内增压曲线存在两个阶段,分别是气液两相共存阶段与液体充满的阶段,前者的压力增加趋势较为平缓,后者的压力增加迅速。后者压力增加的速率大概是前者的9.33 倍。增压平缓阶段即为正常的液氢无损储存阶段,而当罐内充满液体后,增压速率突然增加,这是由于储罐内的液体在等密度变化过程中受环境漏热的影响,温度微小增加而引起的压力急剧升高,极有可能导致罐体内压力超过其设计的安全压力阈值。因此为避免涨罐现象带来罐内的压力骤升,需要设定储存过程中储罐内允许的最大充满率,即终止充满率。终止充满率越大,意味着储罐需要有更大的最大排放速率。由于排放速率与漏热密切相关,大的排放口径意味着大的漏热输入,这不利于维持时间的延长。根据行业标准NB/T47059-2017《冷冻液化气体罐式集装箱》中的规定,对于盛装易燃易爆介质的罐体,初始充满率应不大于90%,储存过程中任何情况下的充满率应不大于95%。

对于不同终止压力下维持时间对应的最佳初始充满率在液氢储罐的生产制造中未给出明确结论,因此基于现有绝热材料工程经验,选取漏热条件为1 W/m2,终止压力分别为0.5 MPa,0.6 MPa,0.7 MPa,0.8 MPa,0.9 MPa 和1 MPa 下,使用俄罗斯模型对相应的最佳初始充满率进行计算,相关结果如图9所示。从图9 可以看出,不同终止压力条件对应的最佳初始充满率相同,都为0.55,这表明终止压力的改变不会影响最佳初始充满率,但会影响对应最佳初始充满率下的维持时间。在储罐的材料与结构强度选定后,其终止压力的选择范围也被确定。对于工业应用,液氢储罐在维持时间满足要求的条件下,适当提高初始充满率是有利于增加工业中液氢储存的经济性。然而,对于不同终止压力,其初始充满率的选取还需要受到标准终止充满率(0.95)的限制。基于图7 的相关结论,在漏热为1 W/m2的条件下,当终止压力达到0.8 MPa 时,为使得储罐满足终止充满率的条件,其对应的初始充满率不应超过0.74。因此,需要对不同终止压力条件下对应初始充满率的选取进行计算。

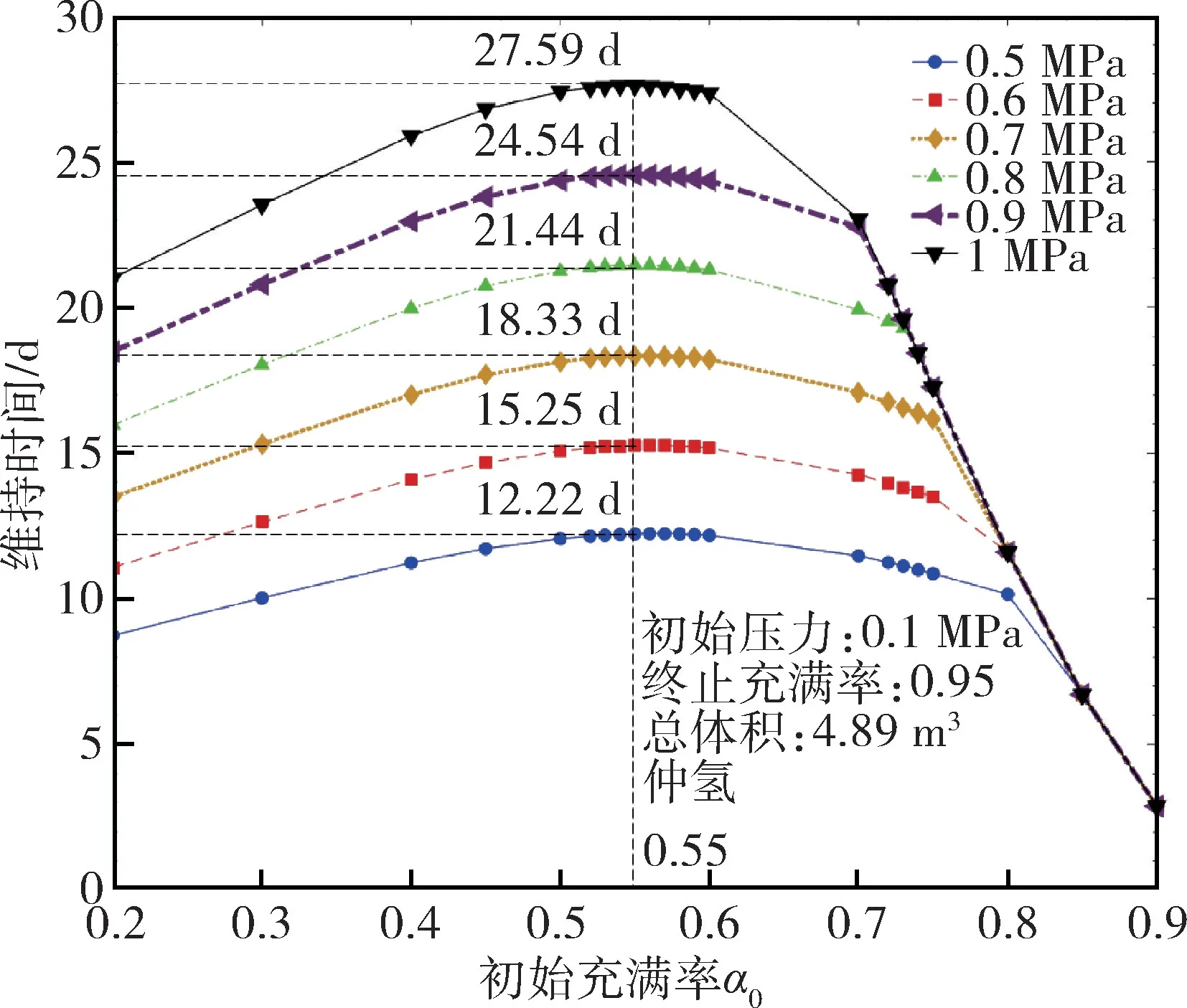
图9 不同终止压力条件下维持时间与初始充满率的关系Fig.9 Relationship between storage time and initial filling rate on different terminated pressure conditions

图10 给出了不同终止压力对应下维持时间、初始充满率和终止充满率之间的关系。从图中可以看出,当终止压力从0.5 MPa 增加至1 MPa 时,对应的临界初始充满率从0.85 减小至0.7,这表明当储罐安全阀设定的终止压力越高,保证液氢无损储存过程中不出现“涨罐”工况所要求的初始充满率就越低。因此尽管在较高终止压力条件下能够保证小型液氢储罐具备较长的维持时间,但一定程度上限制了内部液氢初始充装的液位高度,对长途储运的经济性不利。

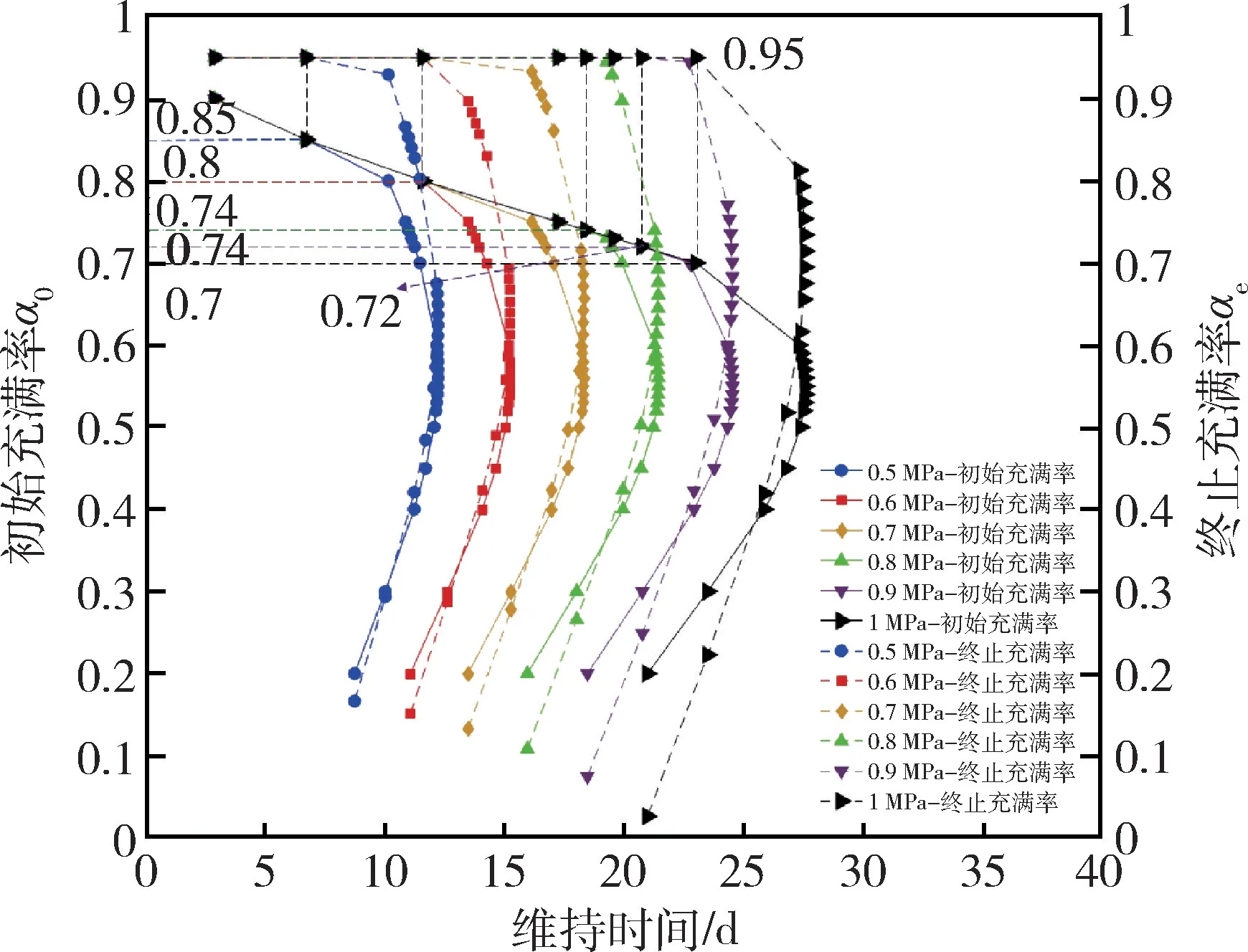
图10 不同终止压力条件下维持时间、初始充满率与终止充满率之间的关系Fig.10 Relationship between storage time,initial filling rate and terminated filling rate on different terminated pressure conditions

4 结论

基于液氢K-site 储罐的饱和均质模型和俄罗斯模型,通过仲氢实际物性揭示液氢低温无损储存的热力行为过程,通过实验数据验证了俄罗斯模型应用于小型液氢储罐增压过程的可靠性,通过模型研究了操作参数对小型液氢储罐最佳初始充满率的影响规律,主要结论如下:

(1)在给定漏热和初始充满率下,俄罗斯模型对于小型低温液氢储罐内压力增长过程具备一定的有效性。模型在初始压力为103 kPa,初始充满率为49%,漏热热流密度为2 W/m2,增压时长为72 077 s(20.02 h)下,预测增压的相对误差为18%。

(2)对于小型液氢储罐,存在一个最佳初始充满率使得储罐维持时间最长,且最佳初始充满率与储罐的漏热和终止条件无关。对于纯仲氢工质,在终止充满率为95% 时,K-site 储罐的最佳初始充满率为55%。漏热越小,终止压力越大,液氢储存时间越大。

(3)为了避免“涨罐”工况的出现,储罐的终止压力限制了初始充满率的取值。计算结果表明,在漏热为1 W/m2下,储罐的终止压力从0.5 MPa 上升至1 MPa时,对应的初始充满率的最大值从85%减小到70%。这说明在储存时间允许范围,可以通过适当降低终止压力来增加初始充装的液体体积。