世界的递归性与辩证法

潘天群

我们周遭的世界由事物构成，这些事物也是我们的思维对象。事物的当下状态是该物先前状态的新的呈现，而当下状态又在以一定的方式构建它的未来，即事物均以“递归”（recursive）的方式在世界中展现。个体的人亦复如是：在与世界的交往中个体的人过往的交往方式构成新的交往的基础，而每一次新的交往又为个体更新的交往积累经验。然而，不同于数学中的递归，事物通过不断否定自己而实现整体性的递归性发展，这正是黑格尔的辩证法所要表明的。本文要探讨的是世界的递归性（recursivity）以及它与辩证法的关联。

一、事物的递归及其内部动力

递归（recursion）是数学中以及逻辑学、计算机科学领域中的一个基本术语。简单说来，如果一个计算过程，它的每一步计算都要调用前一步或前几步给定的或者已经计算出来的结果，那么这样的计算便是递归的。递归函数是一个通过调用自己而被定义在自然数上的函数，如由f（0）=1，f（1）=1，f（n+2）=f（n）+f（n+1）确定的斐波那契数列，它的第三项及以后的每一项是前两项相加而成①自Cristopher Moore（1996），人们开始探索基于实数上的递归函数类及其理论基础，其中微分递归操作数被提出，如Manuel Campagnolo（2002）、José Félix Costa（2009）等人的工作。这里所讨论的递归还是传统上的，即递归是基于可数无穷的自然数之上的。。在递归函数中函数自身被不断调用而生成新的函数值，因而递归机制是一个递进（progressive）机制，即新的数由递归规则被递进地生成。这里不关心数学中的递归，而关心时间与空间中的事物的递归性：事物后续状态遵循一定的规则由前面的状态“发展”或者递进地生成而来。

任何事物都是有限之物，即都有一个与之交互的环境，因而每个事物的递归是在它所在的环境中进行的。于是，事物的递归可以这样形式地描述：某个事物A，A 所处的环境变量E（E是外部变量），A的状态变量X在不同阶段展现为X0，X1，X2，…；其中X0为初始状态。递归规则为Xn+1=f（Xn，E），即Xn+1由先前状态Xn与E 共同确定。这样，事物的递归性可以表示成一个由初始状态、第n阶段的状态和递归规则的三元组：（X0，Xn，Xn+1=f（Xn，E）），即一个特定事物的递归函数为（X0，Xn，Xn+1=f（Xn，E））②在多个事物构成的系统中事物间存在“相互调用”从而构成复杂的递归，此时这个系统中的某个特定事物在某个时刻的状态，依赖于上一状态的自己及系统内其他事物的状态。本文仅考虑作为整体的单个物的递归。。

物的递归函数（X0，Xn，Xn+1=f（Xn，E））刻画了这样的情况，事物面临着开放的环境，它的任一时刻的状态部分地依赖于自身的先前状态，部分地依赖于外部环境，即事物的状态由事物本身与环境共同决定。我们可以用计算机来仿真不同类型的环境变量作为输入参数的事物的递归状态。

有三点需要说明：第一，物的递归函数的某个函数值是事物的某个整体性状态，这个状态包括事物呈现的形状、性质以及事物所含的物质数量等。第二，同类事物可以看成是在环境变量给定的情况下递归规则Xn+1=f（Xn，E）相同，而初始值的不同使同类事物产生出差异性，而不同类事物则可以看成是递归规则不同。第三，若上述递归函数中E为常量C，即环境不再是一个影响事物的变量，则它退化成（X0，Xn，Xn+1=f（Xn，C）），该事物的未来状态由初始状态唯一地确定，这种递归便退化成了数学中的递归。

读者可能注意到，物的递归函数中没有时间变量，而只有前后相继的不同状态。万物在递归中没有统一的自然数可以依赖，更没有连续性的时间作为隐藏的变量控制着不同的事物的发展进程,不同事物的递归有自己的“递归节奏”。时间是我们加于世界的先验形式，通过时间万物的变化次序能够得到理解。

世界中的万物其递归性是显然的。占据着时间与空间的事物在任一时刻的任一具体呈现内含了它的过往，同时又在构建每个事物自己的未来。在这个过程中每个事物在时间中体现了前后相继性与差异性，但是每个事物又保持着自身的同一性。我们两次踏进的是同一条河流，因为第二次踏进的河流是上次河流的延续；但我们又怀疑我们踏进的是否是同一条河流，因为河流在变化之中。

事物的整体性以及整体性的稳定性使得事物的某些性质存在延续性，从而一个事物有别于其他事物，这就是说事物在变化中保持“同一性”。到达终点的忒休斯之船，而不是由神灵将那些在海中被船员丢弃的船的组件拼凑起来的那条“可能的船”，被认为与出发时的船是“同一条船”，因为被修理的船在每一变化中都维持着作为船的本性；而假若中途神灵给忒休斯一模一样的新船，而把忒休斯及其他希腊勇士中途换下来的船用海浪带到终点，则我们不能说忒休斯的新船为原来的船。事物整体性质的稳定性或者延续性使事物成为自身，而不是亚里斯多德所说的本质属性。

事物在其发展过程中保持“同一”，不是说它的物质构成及其数量或者性质保持不变。事物无时无刻都在与环境中的其他物质发生物质、能量与信息的交互直至死亡。然而，在事物发展中存在“同一机制”——事物在发展中努力成为自身而抵抗破解，这可以看成是事物的“同一律”。在逻辑学中同一律、不矛盾律和排中律被认为是“思维三律”。逻辑学家通过挑战或者修改不矛盾律及排中律而发展出新的逻辑，前者如次协调逻辑，后者如多值逻辑。然而，同一律，即A 是A，是难以被挑战的，因为若在思维中同一性不被遵守，A 变成非A，我们的思维会发生混乱而无法进行进一步言说。因而，思维保持同一性是一个基本要求。而在实在层次上，同一性可以看成是一个形而上学预设。例如，生物能够从环境中识别自身与环境并有延续自身的一个机制。

在递归中事物整体地参与到该事物的未来构建，而没有任何一个部分游离于递归进程之外。这是事物递归中的全体参与性。全体参与性即整体性。任何一个事物的部分是整体中的部分，而整体又离不开其各个部分。春天来临，树木的嫩芽长成树叶，它们进行着光合作用，而光合作用生成的营养提供给整个树木。在事物整体性递归中，事物的前后变化中某些性质被继承，一些新的性质会产生；尽管如此，它们是同一个事物。一棵小树，经过春天和夏天的成长，在秋天高大了许多；然而，我们仍说它与春天的树木是同一棵，因为该树木是整体性地向前发展的。

递归是事物继承与变化的外在表现，而发生递归的动力则在其内部。这里要区分两种规则：一是事物状态的外在的递归规则，二是事物内在的“行动规则”。事物状态的递归规则是事物变化的外在表现，它不是变化的内在动力；使事物发生变化的内在动力是事物内部的“行动规则”，这里的行动不表示事物具有像人那样的意向性，而仅指事物针对外部环境的不同的变化而做出的不同反应。兔子群体数量变化服从某种递归规则，但之所以有这样的递归性是因为兔子身体内部的如发情、生育等的生物动力等规则性的生物因素。我们往往从事物内部的行动规则来理解其外在的递归性，科学家正是这么做的。

事物的行动规则是事物本身操作自身及外部事件的行动指令，这些行动指令是内在于事物本身、与事物的物质构成有关。槐树和桑树种子胚胎在同样的土壤中和同样的气候条件下，长成不一样的样子，因为胚胎中潜藏的信息规定它们按照既定的方式发展“自己”。种子胚胎中内在信息便是规则，这样的内在信息或者规则在它们的生命母体即上一棵树中完成了这样的信息编制。宇宙中的万物无例外地会随着时间而消亡，而生命体不过是能够将自己的结构信息保存下来并进行复制以抵抗自身的消亡，但从更大时间尺度来说，这种复制本身也会走向消亡。谈论事物的行动规则意味着赋予自然界的事物以一定的主体性，或者说事物都被看成预先设置了主动应对环境的“程序”。这里的看法是计算主义的。

自然物内在地拥有对本身物质的性质及针对外部事件刺激下的各种操作规则，这些规则表现为事物在空间上和时间上的延展规则，因而，任何一个事物内含的决定事物变化的行动规则是一个集合，即一个事物内含一个行动“规则系统”。某种树木的树干、树枝及树叶分别以特定的形状生长且相互连接，在时间上它们以某种顺序自我成长同时相互支持；而它们在环境中遇到雨水、阳光和风沙等不同的状况，它们有不同的操作规则。

然而，事物的行动规则系统是“不完全的”。完全性（completeness）是逻辑学中的一个基本概念。一个形式系统是完全的，如果其所有的语义有效式能够被语法地证明。这里，我们把逻辑学中的完全性概念做一个拓展：如果一个规则系统对其所处的环境下与它有关联的所有可能出现的状况都能够有一个“有效应对”，那么它就是完全的。在计算机程序设计中一个程序，相对于其目标，应当被设计能够处理所有可能出现的情况，否则这样的程序是不完全的，或者至少有漏洞的（bug）。由于内嵌式程序运行的环境是人工的，完全性是程序设计的最低要求。由于环境是开放的，世界中的事物内部的有限数量的规则系统不可能是完全的。对于任何事物，随时有“意外”发生。“意外”不一定意味着“死亡”，但当事物内含的规则无法应对某种“意外”的时候，事物将不能为其所是，其“死亡”便来临。“死亡”是世界万物的共同命运，这也表明万物内含的行动规则都是不完全的。

事物内部的行动规则构成事物变化的内部动力。本文谈论事物的行动规则而不谈论规律，不是说事物的变化中没有规律。一个植物就像一个工厂，绿叶遇到光能的作用时它内部的叶绿素执行一系列相应的操作，将植物中的水和空气中的二氧化碳转变成糖类和氧气，这是植物在为自身的“生存目的”而执行的一系列指令，而其中的能量转化与守恒、各种元素之间的作用关系等则是规律。因此，规律是宇宙中普遍的或者基本的运行法则，而规则是个性化的事物“利用”规律使自己成为自己的行动指令。科学家不仅仅要研究宇宙中物质的规律，也要研究各个事物运行的内在行动规则。

上面分析的是事物的内部的行动规则，它们的外在表现便是由递归规则Xn+1=f（Xn，E）刻画的递归性。事物的递归性表现在事物的多个方面上，数学对事物的量和形的递归都有刻画。曼德勃罗（B.Mandelbrot）创立的分形（fractal）理论或者分形几何，关心的是“形的递归”：在形的递归中“形的递归规则”生成了部分和整体的自相似的几何形状。数的递归能够刻画事物状态量的递归性，而分形几何能够刻画事物形状的递归性。而在设计方法论中，曾勇和程耿东给出了人类设计中的递归推理特征，他们认为，每一步设计方案是下一步更加完美的设计方案的基础，一个完善的方案在递归中完成①Zeng Yong,Cheng G.D.,“On the Logic of Design”,Design Studies,1991,No.12,pp.137-141.。若我们把设计者内化为设计之中——这是完全可以想象的，设计者便成为一个设计智慧体。给出设计方案便是该类智能体的唯一行为，这样的行为是递归的，而使设计智能体产生递归性的是智能体的关于设计的学习机制。

有两个特殊的递归规则。第一种，某个事物在某个状态以后，其后续状态保持“不变”，即事物保持为“常态”。“常态”是递归的平庸态或者不足道态（triviality）。我们用C表示这种“常态”或者“平庸态”。用函数表示为（Xk=C，Xk+1=Xk）：从k状态开始后的每一个状态都是常态C。处于这样的递归态中的事物，变化消失了，事物自身所含的变化或者发展的力量便是事物自身的否定性，处于平庸态的事物其否定性彻底丧失了。这样的“事物”若从开始便是这样的状态，我们说，它可能只是一个暂时的集合体，而不能称为“一个事物”。变化是事物的本性，一个事物蜕变为常态，表明它失去了“变化”，此时它便丧失了作为一个事物的本性。平庸态的事物只存在于理念（包括数学中）世界中，而现实世界中的万物都处于变化之中。

第二种，某个事物在某个状态后其后续状态为“无”，即事物作为它自己被彻底终止，而成为“空无”。这是事物的“空无态”，我们用Φ 表示这种“空无态”。用递归函数表示即为（Xk=Φ，Xk+1=Xk）：从k阶段开始，事物便为空无态。事物达到空无态时事物自身招致最大的否定性。世界中的万物是有限的，这个有限性不仅在空间的占据上是有限的，在时间的占据上也是有限的，即事物最终都走向空无态。空无的后续状态还是空无，从这个意义上说，这种“无”的特殊状态是第一种的特例。

“平庸”和“空无”是两种特殊的递归状态，事物的递归往往介于它们之间。递归是自然物（包括作为个体的人本身以及人类社会）的自然属性，这个自然属性在事物的历史进程中得以体现。

要说明的是，前面已经表明递归中操作是“递进地”被执行着，或者潜在地被执行着，初始值或者前面的执行结果通过规则生成新的值，递归性即递进性（progression）。从前面斐波那契数列的简单例子中就可以看到这点。这里要说明的是，之所以我们称之为递归或者调用自身，是因为在我们心中有“规则优先”这种理念：规则在先且被给定，它通过不断地“后退调用”已知的或者已经计算得到的实体（数值或者事物）而生成新的实体。而如果我们以“实体优先”理解递归，那么，新的实体能够在给定的初始的实体通过规则不断地“向前递进”地生成。这样，递归可以理解成规则给定下的“后退”（backward）寻找且运算“自己（实体）”，而递进则是实体给定下通过规则“向前”（forward）不断地生成自己。

二、离散性的世界观

事物的递归性表明，事物根据内含的规则针对外部环境中的事件的发生而计算并行动着，这意味着事物的变化是离散的。因而，与事物递归性发展相应的世界观是离散性的世界观。这里的离散性是指事物的外部环境是离散地变化的，事物相对于环境的变化也是离散的。

连续性或离散性概念描述的是两个量变化之间的关系。某个量x的变化相对于另外的某个量α的某个区间上是连续的，如果在该区间中的任一个地方当α的变化趋于0时x的变化量也趋近于0。我们惯常的变化往往被理解为某个量相对于时间上的变化，这样的变化可以是事物整体位置相对于时间的变化，事物的整体或者其部分形状相对于时间的变化。我们预设了时间在连续地向前流逝。然而，我们见到的不是具体的时间，而只是各种发生的事件，而每个事物面对环境中的事件执行着某个程序，这种变化是非连续的。常温下的种子维持着活力，遇到雨水发芽，遇到高温则失去成长的能力……它的体内拥有的行动规则根据外部环境中的不同事件进行不同的操作。我们往往因无法分辨那种跳跃性，而猜测事物是连续的。

由于数学与近代科学的发展，“世界是连续的”成了我们的信念并且已经教条化。牛顿的《自然哲学之数学原理》不仅开启了用数学研究物理世界规律的方法，而且给我们提供了连续性的世界观。近代数学与物理学在世界连续性信念上是相互支持的。在数学教科书中我们学了许多连续函数以及它们的性质，我们熟知且习惯于它们。微积分中能够微分的一定是连续的，而在某个区间某个函数除了有限个点或者最多可数无穷个点处不连续外其余地方要连续，它才能够可积（黎曼积分）。非连续函数，它们的性质被认为怪异，处理起来麻烦，而不被我们喜欢。在物理学中，我们用微分方程表达物理系统的状态及其动力学性质，以至于拉普拉斯说，如果我们知道某个系统的初始状态以及该系统的规律，则我们能够知道它未来任何时刻的状态。

连续性信念在我们认识世界中作用巨大，然而，它并非真理。微观物理学告诉我们微观世界中粒子及其变化是非连续的：粒子的衰变是释放一个个微小粒子（如α粒子）进行的，原子核外电子通过层级跃迁而释放或吸收普朗克常数的整数倍的能量，等等。而分形理论告诉我们，实际上事物的形状不是连续的，而是离散的，比如海岸线，分形几何被认为是大自然的几何。

事物的发展是离散的还是连续的，往往取决于我们的心中的预设。一窝兔子中兔子的数量在指数增长，该兔子群体是递归性的，也是离散的：任何一个时段的兔子数量是下一个时段的兔子数量的基础。如果我们把兔子数量看成一个总体，那么这个总体是离散地变化的。我们不愿意把一窝兔子看成是一个整体，因为我们知道一窝兔子只是一个个兔子的集合，没有一个性质能够作为本质而将这窝兔子东西与其他东西区别开来。然而，假若我们根本无法识别个别的兔子，而将一堆兔子看成一个整体——这是完全可能的，此时兔子的整体便是在离散地增长与变化。事实上我们观察微生物或者未知世界的“某个对象”时，我们就是这么做的。

如果世界的变化是连续的，那么我们要找的便是这样的以连续函数所表示的规律，在这方面我们做得已经很成功了。而如果世界的变化是离散的，那么，为了认识事物的递归性，我们需要做的便是寻找事物内部的行动规则——根据环境而做出应对的行动指令。事物或者事物的部分可假定保持不变，除非遇到外部的触发事件。事物的变化可以看成是其内部的行动指令对外部的事件的“应对”。而由于外部事件或者发生或者不发生，因此事物的变化是离散的。

离散的世界观是非决定论的。事物的变化是事物质料参与的递归，质料本身的惯性使事物在发展中保持着“持续性”。一只鸡的可能的体型、重量等依赖于环境，而无论在何种环境下它不可能长成鸡之外的其他形状的动物。但是，事物某个时刻的状态与规则影响或者构建事物后续的状态，但这不等于说，它是完全被决定了的。数学中我们所讨论的递归函数是被递归规则及初始函数值所完全决定。而世界中的事物其环境是开放的，因而事物在某个时刻遇到某个外部事件是偶然的，事物在任何时刻的状态是偶然的。我们无法将事物的递归函数转变为时间上的连续的、能够唯一地确定事物未来任意时刻的状态的函数，除非环境变量是在先被给定的。设想基因等各方面完全一样的两个新生婴儿，他们在不同的环境中成长，经过足够长的时间，无论是长相还是行为方式可能会变得显著不同，原因在于环境中的变量会影响到孩子的每一步成长，而每一步的些微差异又影响到下一步的变化。这就是说环境使得事物呈现偶然性与独特性。这正如许煜（Hui Yuk）说：“递归性不仅是机制的重复；它由回到自身以便决定自身的环形运动所刻画，而每个运动都是向偶然性开放的，这因而决定了它的独特性。”①Yuk Hui,Recuisivity and Contingency,London:Rowman&Littlefield International Ltd.,2019,p.4.

需要说明的是，即使环境变量能够被预先给定，在已知事物的递归规则情况下，我们也无法预先计算出事物的未来状态，正如非线性（复杂性）科学告诉我们的迭代运算高度依赖于初始值；在有些情况下迭代运算对初始值高度敏感，而出现混沌现象。递归尽管不同于迭代，每次递归都是事物本身的一次展现，但事物的递归是否会出现混沌则是一个需要我们进一步分析的话题。

三、辩证法：刻画事物递归性的本体论和作为递归性算法的思维方法

哲学家们希望用尽量少的概念构建普遍性的理论以解释世界，黑格尔的辩证法便是这样的理论。黑格尔的辩证法既是本体论又是认识论：作为本体论，辩证法认为，事物中矛盾推动事物不断否定自己；而作为认识论，我们根据正反合这样的辩证思维对事物的认识越来越深化。

作为本体论，黑格尔说：“持续性辩证法是现实世界中一切运动、一切生命，一切事业的推动原则……举凡环绕着我们的一切事物，都可以认作辩证法的例证。”②黑格尔：《小逻辑》，贺麟译，北京：商务印书馆1997年版，第177-179页。在黑格尔那里，辩证法的对象是有限物。“凡有限之物，莫不扬弃自身。”③黑格尔：《小逻辑》，第176页。无限之物不在时空之中、没有边界，它们是我们所无法思维与叙说的。他说：“有限物作为某物，并不是与别物毫不相干地对峙着，而是潜在地就是它自己的别物，因而引起自身的变化。”④黑格尔：《小逻辑》，第206页。事物被我们所思维，在我们的思维中它们被我们识别并被区别于其他事物。事物区别于其他事物，这个区别不仅仅指某个时刻它所拥有的各个组成以及关系，而且包括操纵这些组成及关系的规则与力量。这种区别可以说是事物本质上的区别。这样的事物在时间与空间中产生，在时空中生成与变化，同时又消亡。

黑格尔认为是矛盾推动事物的发展。黑格尔说：“凡有限之物都是自相矛盾的，并且自相矛盾而自己扬弃自己。”⑤黑格尔：《小逻辑》，第177页。变化与发展便是黑格尔所说的否定性，事物的否定便是事物蕴藏这使自己改变当下状态的力量。黑格尔说：“花朵开放的时候花蕾消逝，人们会说花蕾是被花朵否定了的。”⑥黑格尔：《精神现象学》，贺麟、王玖译，北京：商务印书馆1979年版，第2页。在很多人看来矛盾是不能客观地存在的，因而说矛盾推动事物的否定性，是荒唐的，这也是许多人反对黑格尔的原因。推动事物发展的或者使事物产生与当下状态不同的不是矛盾——事实上矛盾是不能存在的，而是事物本身内部的规则（规律），即否定性——事物的不同状态——是结果，不是原因。花蕾与花朵是花的前后相继的两种不同状态，是花及支撑花的整个植物的内部的力量使得花蕾变成了花朵，说花朵让花蕾不再是花蕾是错误地将结果看作了原因。

黑格尔的辩证法中含有递归性，因为辩证法强调事物的继承与发展。同时这里的递归性含有辩证元素，因为事物从一个状态X1转变为另外一个的状态X2，无论是X1还是X2，我们都说它是该事物的具体呈现。从X1到X2的这样的转变便是A 自身否定性的体现，通过这种否定A 得以发展或者变化。在这样的过程中，事物的自我否定性体现在该事物在时间上的不同，但同时保持着自身的同一性。对之，许煜说：“递归既是结构的又是操作上的，存在与生成的对立通过递归被扬弃。扬弃保持了这种对立（正题与反题）因而也提升它们到一个第三者（合题）。”①Yuk Hui,Recuisivity and Contingency,pp.4-5.

在黑格尔那里，理性与实在是同一的，因而在黑格尔那里辩证法既是思维的规律又是实在的规律。我们的理性通过自身的力量达到对事物的最终真理的认识，此时辩证法可以被理解为理性思维的方法。理性执行着辩证思维，这是可理解的，而将理性看成是事物的否定性的推动力量则是错误的——推动事物发展的不是理性的力量，而应当是事物自身的规律（规则）。下面我们来看辩证法作为思维的规律的递归性。

辩证法的结构是，从正题到反题，到合题——新的正题，新的反题……我们对事物的认识中任何一个阶段的认识——正题还是反题抑或其合题——都是对事物的认识，而任何一个都是不完满的；要达到对事物终结真理的认识，需要一个无限的辩证过程。黑格尔的辩证法就是一个思维的递归性算法。

我们引进“否定”和“综合”为两个操作算子：“否定”是一元运算元，其运算对象是正题，而“综合”是二元操作数，它的运算对象是正题与反题。假定初始的正题是f0，f0的反题便是f0-，由f0和f0-的“合题”为f（1f0，f0-），相应地，f（1f0，f0-）的反题为f（1f0，f0-）-，简写为f1-。一般地，对于第n个阶段的正题fn和其反题fn-，其合题为fn+（1fn，fn-）。辩证法便是这样一个递归过程：

在辩证过程中，给定初始正题f0，递归便能够进行了：给定的初始正题f0，它的反题通过正题的否定而产生f0-，而合题f（1f0，f0-）是通过对f0，f0-的“综合”而产生。辩证法的递归性公式可以表示成一个四元组的递归函数：通过递归，新的正反合三元素便不断地产生。

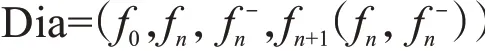
对于上面将辩证法刻画成递归性算法，有三点需要说明。

辩证法在本体论上所说的否定，指的是同一个事物的变化，而无论是否定、还是否定之否定，事物还是同一个事物；这就是为什么黑格尔说事物的否定之否定是扬弃——扬弃是同一个事物的自身的不断发展。

第二，合题（synthesis）不是正题和反题的合取。一个正题fn和它的反题fn-的合题fn+（1fn，fn-）是综合，而不是形式逻辑意义上的合取，因而，合题同样不能从正题与反题中逻辑地得到，任一合题fn+（1fn，fn-）也自然不是（逻辑）矛盾。在辩证思维中合题吸取了正题和反题的“部分真理内容”，而实际的事物状态中后续状态体现了原来状态的继承同时有新的变化。因而在合题fn+（1fn，fn-）中有足够的空间容纳正题和反题，不同的人能够创造性地得到不同的合题。即使正题与反题从形式上是“不同的”，其合题是更高层次的综合，而不是矛盾。国内国外学者试图通过对经典逻辑的修正给出次协调逻辑,如达·科斯塔、普利斯特等人的形式化工作。他们通过对否定词的改造，在系统中允许有意义的“矛盾”，这种做法确实丰富了逻辑学研究，尤其是辩证逻辑的研究，这一点正如桂起权等所认为：“次协调逻辑为辩证逻辑的形式化提供了比较现实并且极有希望的新途径。”①桂起权、陈自立、朱福喜：《次协调逻辑与人工智能》，武汉：武汉大学出版社2002年版，第111页。这些学者同时给矛盾以本体论解释，如普利斯特所做的那样②Graham Priest,“Paraconsistency and Dialetheism”,Handbook of the History of Logic,2007,Vol.8,pp.129-204.。然而，这些工作只是黑格尔意义上的辩证逻辑的初步探索，因为“综合”是有丰富内容的思维过程，而不是普利斯特的简单的“双真命题”所能够刻画的。

这里，每一阶段的正题可以看作是对事物的“局部认识”，而反题是在正题基础上与正题不同的认识，因而是对正题的“否定”。反题也是对事物的局部认识，也是关于事物的部分真理。这样，合题中的真理性比正题、反题的真理性“要多”。通过不断的正反合，主体对事物的认识走向最终的真理。波普尔（Karl Popper）反对辩证法，但是在认识论上波普尔至少承认辩证法的诠释性作用的：“必须承认，对思想史的这样一种辩证诠释有时可能是完全令人满意的。”③波普尔：《猜想与反驳》，傅季重译，上海：上海译文出版社1990年版，第450页。当然，波普尔强调试错法，因为在他看来科学中最重要的是创新，因而他认为试错法比辩证法更好，“用试错法做诠释可以说比用辩证法做诠释的范围稍微广泛一些。”④波普尔：《猜想与反驳》，第449页。波普尔的猜想与反驳的也是一个思维算法，然而这个算法中只强调否定性而否认继承性。

第三，辩证法可以有多种形式，而不仅仅是Dia=（f0，fn，fn-，fn+（1fn，fn-））这样的简单三段式。对于任何一个正题，它能够有多个反题，因而其合题不是简单的正题与一个反题的综合。比如对于正题f0，人们找到了f0的两个反题f0-1，f0-（2当然反题可能不止两个），此时，在此基础上的合题是对前三项的综合f（1f0，f0-1，f0-2）……因此，我们可以构造多种递归形式的辩证法。

递归性体现在人类的思维及各种活动之中，思维活动中的递归性在一定意义上说就是继承与发展。正反合辩证法是这样一个递归性算法：当有了正题之后，人们会考虑它的局限性，因而会考虑或者试图给出与之不同的反题，而一旦有了正题与反题，人们自然会试图对之进行综合。对于辩证思维，辩证法没有告诉我们如何给出初始的正题，它也没有告诉我们如何得到反题以及在有了反题之后如何进行综合。因而，辩证法可以用在解释性的方法论，而不能用作指导性的或者预测性的方法论。

辩证法只是人类的“一种”思维算法，人类还有其他不同于辩证法的思维算法，如波普尔的证伪方法或者“试错法”，以及拉卡托斯（Imre Lakatos）的科学研究纲领方法论，这些思维算法或者具有递归性或者没有递归性。哪种思维算法更好、更有助于我们认识真理？这本身也是一个重大的认识论问题。

四、结束语

本文提出事物的递归性并对之进行了刻画，同时分析了递归性与辩证法之间的融通。事物的递归性表明事物的变化中的继承与发展。辩证法可以刻画事物的这种递归性。辩证法中的否定性应该理解成变化，而这种变化本身不能构成推动事物的力量，它们是结果；事物本身的内部规则递归性的使用是事物否定性产生的原因。

事物通过自身内部的行动规则在环境中递归性地延展自身。这种递归性是对世界进行科学研究的世界观，同时也能够是方法论：我们要确定不同事物的递归性特点并寻找内部的行动规则。我们给出的世界的递归性的观点，不是在提供一个绝对真理，只是尝试地给出一个新的世界观与方法论，希望这样的观点对我们进一步认识我们身处的世界有所帮助。