基于麻雀搜索算法的工业互联网入侵检测方法
2022-09-08罗俊星陈志翔
罗俊星 陈志翔
(1. 漳州职业技术学院 信息工程学院, 福建 漳州 363000;2. 闽南师范大学 物理与信息工程学院, 福建 漳州 363000)
0 前 言
工业互联网作为全新工业生态、关键基础设施和新型应用模式,通过人、机、物的全面互联,实现了全要素、全产业链、全价值链的全面连接[1]。工业互联网安全面临着诸多严峻的挑战,如震网病毒、乌克兰电力系统遭受攻击、德国核电站感染病毒、勒索病毒等。作为工业互联网体系架构中的一项重要安全技术,入侵检测技术能够检测出异常操作。
结合神经网络和深度学习来优化入侵检测技术是一个研究方向。池亚平等人提出了基于GR-CNN算法的网络入侵检测模型,采用增益率算法和卷积神经网络算法来提高模型泛化能力[2]。张定华等人提出了从传统网络到工业网络的数据流特征知识迁移思想,利用卷积神经网络处理数据流特征,实现了异常检测[3]。
群智能算法具有控制参数少、易于实现、全局寻优能力强等特征,常应用于数据挖掘、组合优化等方面。张瑞等人提出了基于自适应变异粒子群优化算法(SVPSO)的入侵检测模型,将遗传算法的变异思想引入PSO算法中,以优化SVM分类器参数[4]。耿志强等人提出了一种融合随机黑洞策略的灰狼优化算法,利用随机黑洞策略更新种群位置,保持了算法的局部搜索能力[5]。
机器学习能在庞大的数据中识别未知攻击,被广泛应用于入侵检测领域。赵国新等人提出了基于HAQPSO优化极限学习机的入侵检测模型,利用差分策略和Levy飞行策略进行参数寻优[6]。陈鑫龙等人提出了基于机器学习的Modbus_TCP通信异常检测方法,结合决策树分类模型能够有效地识别出Modbus_TCP流量中的异常数据[7]。何戡等人提出了一种基于X-Boost算法的包裹式特征选择方法,提高了入侵检测效率[8]。
基于前人的研究成果,本次研究提出了一种基于改进麻雀搜索算法(LSSA)的工业互联网入侵检测方法,通过Logistic混沌映射和Levy飞行策略来优化KELM分类器参数。
1 麻雀搜索算法
麻雀搜索算法(sparrow search algorithm, SSA)是薛建凯等人提出的一种群智能算法,把麻雀划分为发现者和加入者,发现者具有较好的适应度,负责较大范围觅食和为加入者提供搜索方向,同时部分加入者会通过跟踪发现者来抢夺食物[9-10]。每次迭代时,发现者通过式(1)更新位置:
(1)
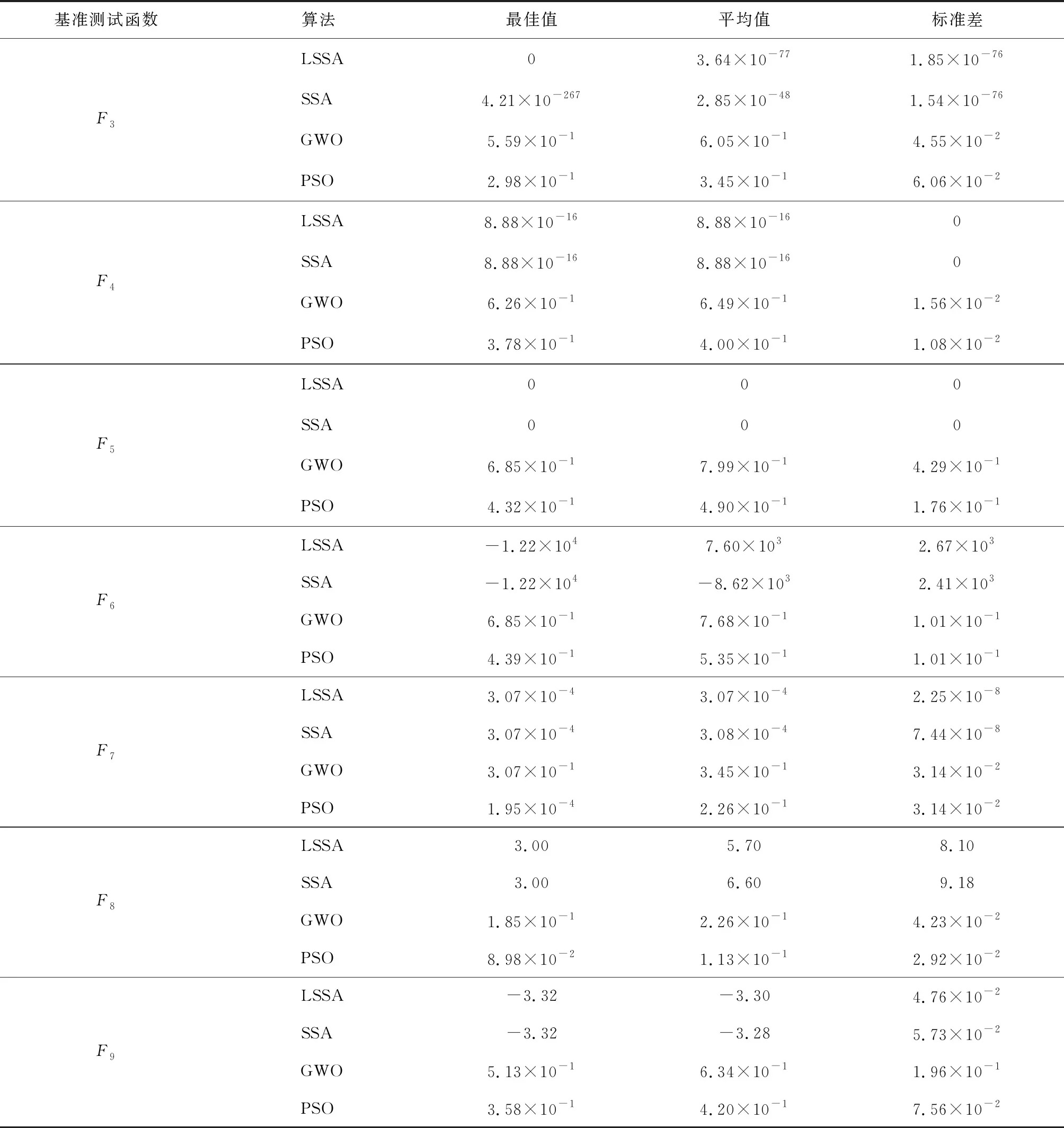
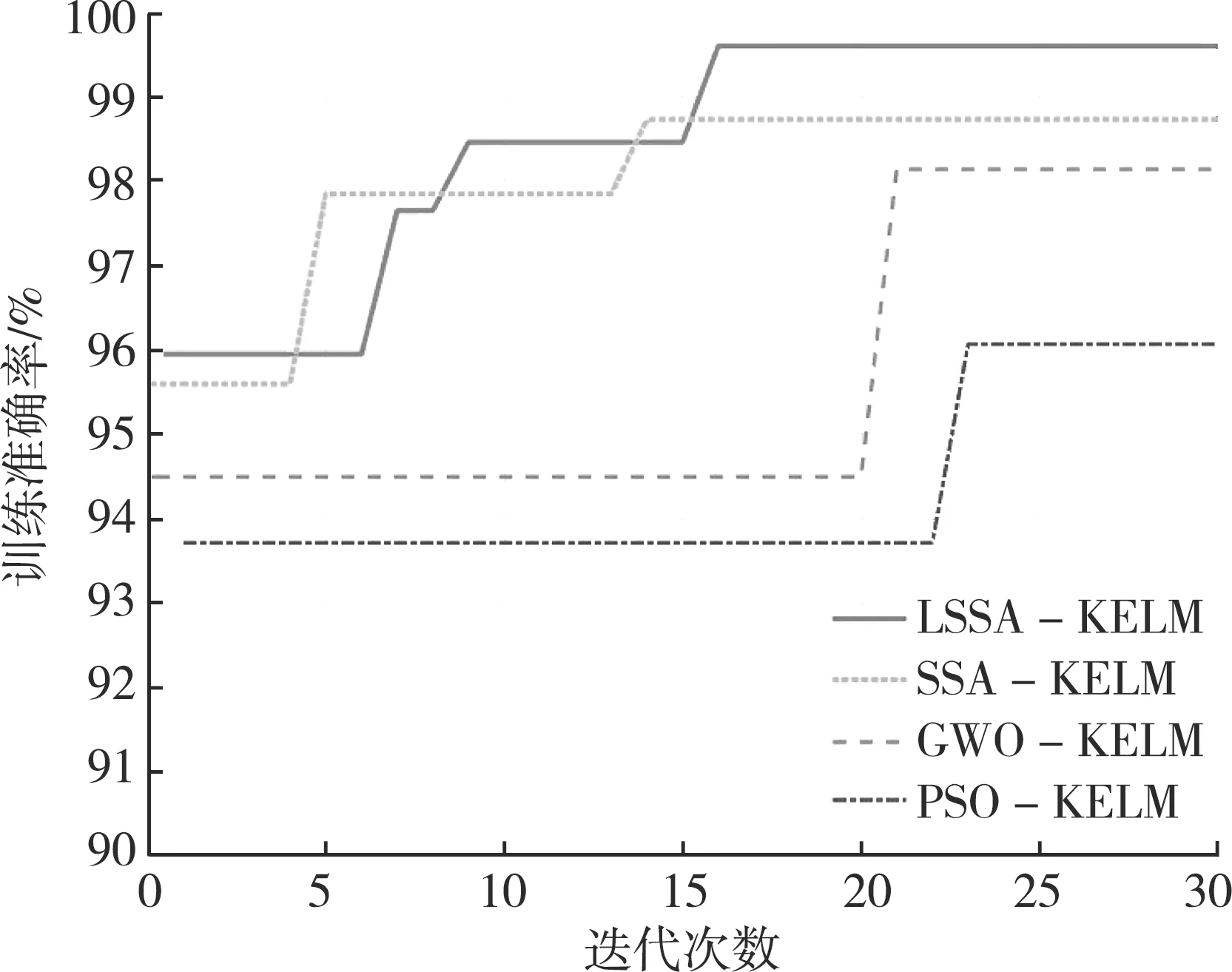
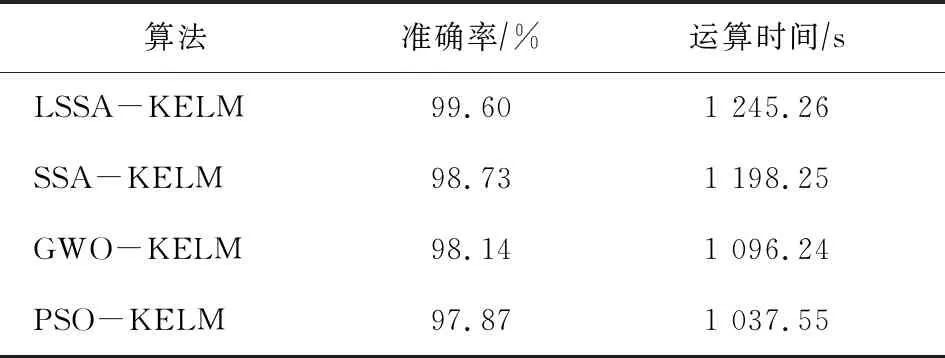
式中:Xij,t为第t次迭代时第i个发现者在第j维中的位置;tmax为最大迭代次数;α为随机数,α∈(0,1);Q为服从正态分布的随机数;L为1×d的矩阵,矩阵内每个元素均为1,d为待优化问题变量的维数;R2为预警值,R2∈[0,1];ST为安全阈值,ST∈[0.5,1]。R2 加入者通过式(2)更新位置: (2) 式中:A为1×d的矩阵,矩阵内每个元素随机赋值为1或-1,A+=AT(AAT)-1;Xp,t为第t次迭代时发现者占据的最佳位置;Xw为当前全局最差位置;N为麻雀数量,i>N/2表示第i个加入者觅食失败且适应度值较差,需要转移搜索方向。 令发现危险的麻雀为总数的10%~20%,初始位置随机。当麻雀发现危险时,通过式(3)更新位置: (3) 式中:Xb,t为第t次迭代时全局最佳位置;θ为步长控制参数,是服从正态分布的随机数;K为随机数,K∈[-1,1];ε为极小常数;fb为当前全局最佳适应度值;fw为当前全局最差适应度值;fi为第i只麻雀的适应度值。 SSA算法的局部搜索能力强、收敛速度快,但全局搜索能力较差,容易陷入局部最优[11],因此本次研究采取Levy飞行策略来优化SSA算法。 Logistic混沌映射生成的数据具有较强的遍历性和自相关性,能够提高初始种群的多样性[12-13]。本次研究运用Logistic混沌映射来取代麻雀种群初始化的随机映射。Logistic混沌映射的数学表达式如式(4)所示: yM+1=yM×λ×(1-yM),yM∈(0,1) (4) 式中:M为迭代次数;λ为Logistic参数,λ∈[1,4],λ值越大,映射分布越均匀。 当λ=4时,Logistic混沌映射工作处于完全混沌状态。 Levy飞行策略是一种频繁的短距离跳跃和偶尔的长距离跳跃相结合的非高斯随机过程,能够避免算法陷入局部最优[6,14]。Levy飞行策略的公式如式(5)所示: (5) 式中:ω一般为1.5;u、v为[0,1]区间的随机数。 σ的计算如式(6)所示: (6) 其中: Γ(x)=(x-1)! 随着迭代的进行,将Levy飞行策略公式代入式(2)可得: (7) 结合Logistic混沌映射和Levy飞行策略的LSSA算法流程如图1所示。 图1 LSSA算法流程 为了验证LSSA算法的性能,本次研究基于 9个基准测试函数对LSSA算法、SSA算法、灰狼算法(GWO)和粒子群算法(PSO)进行对比分析。基准测试函数及参数设置如表1所示,F1—F3是单峰函数,F4—F6是多峰函数,F7—F9是固定维数函数。算法参数设置如表2所示。将每个基准测试函数作为目标优化函数,每个算法独立运行30次,计算其最佳值、平均值和标准差,对比结果如表3所示。 表1 基准测试函数及参数设置 表2 算法参数设置 表3 算法对比结果 续表3 由表3可知,对于单峰函数F1—F3,应用LSSA算法都能得到理论最佳值,且平均值和标准差最小,说明LSSA算法的收敛精度和鲁棒性优于其他3种算法。对于多峰函数F4、F5,LSSA和SSA算法的性能相当;对于多峰函数F6,LSSA算法的收敛精度和鲁棒性比SSA算法略差、比GWO算法强,PSO算法的标准差最小。对于固定维数函数F7、F9,LSSA和SSA算法都能得到理论最佳值,但LSSA算法的收敛精度和鲁棒性优于其他算法;对于固定维数函数F8,LSSA和SSA算法都能得到理论最佳值,但LSSA算法的收敛精度和鲁棒性优于SSA算法。综上所述,相较于SSA、GWO和PSO算法,LSSA算法更能得到全局最佳值,且收敛精度和鲁棒性更优。 HUANG G B等人提出的核极限学习机(KELM)是指在极限学习机(ELM)的基础上引入核函数,只需要输出权值矩阵β便能得到最佳值,具有控制参数少、泛化能力强和学习速度快等特点[15-17]。 给定n个任意样本(Xi,ti),Xi=(xi1,xi2,…,xin)T∈Rn,ti=(ti1,ti2,…,tim)T∈Rm。设单层神经网络有l个隐藏神经元,则极限学习机输出公式如式(8)所示: Hβ=T (8) 式中:H是隐含层输出矩阵;β是输出权值矩阵;T是期望输出矩阵。 根据KKT理论得出: (9) 式中:C是正则化系数;εi=[εi1,εi2,…,εim]是训练输出与样本原始值的误差;aij是第i个样本的第j个输出节点的拉格朗日乘子;h(xi)是H的行向量。 式(9)中的参数优化条件如下: (10) 求解式(9)、式(10)可得: (11) 式中:I为单位矩阵。 引入核矩阵可得: Ω=HHT=h(xi)h(xj)=k(xi,xj) (12) 求解式(11)、式(12)可得: (13) 求解式(8)、式(13)可得KELM的输出权值: (14) 综上所述,只需要确定核参数与正则化系数,即可得出KELM的输出权值。本次研究采用LSSA算法来优化KELM的核参数与正则化系数,核函数选择局部能力较强的高斯核函数,利用训练集训练入侵检测模型,评估测试集。LSSA-KELM入侵检测算法流程如图2所示。 图2 LSSA-KELM入侵检测算法流程 本次研究使用KDD CUP 99的10%数据集模拟工业互联网入侵检测,其中训练集和测试集各4 000条记录。数据集分为Normal、DoS、Probe、U2R、R2L等5类;攻击类型又细分为39类,每条数据包含属性特征41个、类型标签1个[18]。各数据集中的数据类型及数量如表4所示。由于数据集属性特征值中包含大量文字,如protocol_type属性的icmp值、service属性的domain_u值等,这些特征值无法在LSSA-KELM中识别,导致检测效率降低。将数据集中的文字特征向量按照陈兴亮提出的方法进行数字编码[19],将Normal、DoS、Probe、U2R、R2L分别记为0、1、2、3、4。数据集中的有效属性特征合计33个,其余8个属性特征不影响分类结果,可以删除[20]。由于有效属性特征值的大小差异悬殊,因此采用Matlab中的mapstd函数进行标准化处理。 表4 各数据集中的数据类型及数量 仿真环境为Window 10(64位),Matlab2016a,Intel i5-6200U CPU, 8 Gib内存。 本次实验对SSA-KELM、GWO-KELM、PSO-KELM与LSSA-KELM算法进行对比分析。种群数量为20,最大迭代次数为30,维数为2,核参数和正则化系数的搜索区间为[10-5,105],其他参数设置如表2所示。采用准确率、误报率、漏报率、精确率和召回率等指标来评价算法的优越性。 5.3.1 训练结果分析 由不同迭代次数下4种算法训练准确率的对比结果(见图3)可知,LSSA-KELM算法的准确率最优,达到99.60%,约在第16代收敛到最优值;SSA-KELM算法约在第14代收敛,速度最快;GWO-KELM算法约在第21代收敛;PSO-KELM算法约在第23代收敛。由4种算法训练准确率和运算时间的对比结果(见表5)可知,由于加入了Logistic混沌映射和Levy飞行策略,LSSA-KELM算法的运算时间比SSA-KELM算法多47.01 s。 图3 不同迭代次数下4种算法训练准确率的对比 表5 4种算法训练准确率和运算时间的对比 5.3.2 测试结果分析 由4种算法的测试结果(见表6)可知,LSSA-KELM算法的准确率最高,PSO-KELM算法的准确率最低;LSSA-KELM算法的精确率和召回率最高,分别为96.38%和87.02%;LSSA-KELM算法的误报率和漏报率最低,分别为6.08%和12.99%。 表6 4种算法的测试结果 由4种算法的样本数据检测率对比结果(见图4)可知,LSSA-KELM算法对DoS、Probe、U2R、R2L等 4种攻击类型数据的检测率比其他算法高,各算法对Normal数据的检测率差别不大。 4种算法的准确率和召回率偏低、误报率和漏报率较高,与数据结果差异较大,这可能是由于测试集数据不平衡,导致有些数据类型的检测率偏低。通过各项指标的对比结果可知,LSSA-KELM算法的检测率高于SSA-KELM、GWO-KELM、PSO-KELM算法。 入侵检测是工业互联网安全技术之一。本次研究提出了基于Logistic混沌映射初始化麻雀种群和Levy飞行策略的LSSA算法,对KELM进行核参数和正则化系数寻优,建立了LSSA-KELM工业互联网入侵检测模型。利用KDD CUP 99的10%数据集进行仿真实验,对SSA-KELM、GWO-KELM、PSO-KELM与LSSA-KELM算法进行对比分析。结果表明,LSSA-KELM入侵检测模型对是否遭受异常攻击和攻击数据类型的识别能力更强。2 改进麻雀搜索算法
2.1 Logistic混沌映射
2.2 Levy飞行策略

3 改进麻雀搜索算法的验证



4 基于LSSA-KELM的入侵检测算法
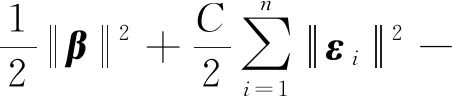

5 仿真实验与分析
5.1 数据集及预处理

5.2 仿真环境、相关参数设置及评价指标
5.3 仿真实验结果与分析

6 结 语
