基于FRA的变压器绕组径向变形定位和量化方法研究

2022-09-08宋云东苑经纬韩洪刚王冠宇

南京理工大学学报 2022年4期

宋云东,苑经纬,韩洪刚,王冠宇,郭铁

(国网辽宁省电力有限公司电力科学研究院,辽宁沈阳 110006)

变压器运行过程中,可能受到电磁力或机械冲击,导致绕组在轴向和径向上变形[1,2],进而导致变压器故障,影响电网的经济安全运行。因此,有必要对变压器绕组位移和变形进行检测,预防绕组变形进一步恶化,从而最大限度地保证变压器不发生故障。

检测变压器绕组几何形状变化的传统方法是漏感测量[3],但这个方法只能用于检测径向变形,轴向变形测量需要采用更精确的测量方法。Dick等[4]提出了用频率响应分析(Frequency response analysis,FRA)来检测绕组位移和变形。黑箱变压器模型[5-7]是FRA数据分析方法之一,FRA中的任何变化都将导致模型参数变化,进而可知变压器内部结构变化。Bigdeli等[8]使用神经网络根据模型参数变化对故障进行分类。另一种是白箱变压器模型,Mitchell等[9]研究了白箱模型参数对FRA的敏感性,通过修改模型在整个绕组不同位置的串联电容来模拟变形和位移故障;Duvvury等[10]改变了电容和电感模型参数,以模拟绕组变形;Samimi等[11]利用更高频率的FRA来检测研究微小绕组变形和位移。但黑箱模型取决于变压器拓扑结构及相应故障参数,仅从输入输出特点判断变压器绕组变形的模型,无法反映输入输出的内在联系,而白箱模型需要变压器的具体参数,利用数学工具建立输入、输出之间的内在联系的模型,这种模型的实施难度随着系统的复杂程度增加而成倍增加。

因此,基于变压器的几何参数和材料特性,建立了变压器灰箱模型[12,13],既保留了重要的变压器参数,又简化了计算过程;提出了一种非破坏性方法,通过改变变压器模型中的适当参数值,模拟了不同程度的绕组变形;对1.3 MVA 11 kV/433 V Dyn1配电变压器的屈曲试验,对FRA结果进行了分析,并将模型成本函数基于FRA值进行拟合,得到变形后的模型参数值;最后为验证FRA方法在绕组变形检测中的有效性,将变形后的参数值与有限元分析(Finite element analysis,FEA)确定的参数预测结果进行比较,结果证明了所提出方法的有效性。

1 通用相变压器模型

本节详细介绍了通用相变压器模型——灰箱模型。

1.1 模型结构

变压器建模有100多年研究历史。本文采用通用的n段集总参数模型进行FRA分析,由于可能连接的端子组合不同,通用相位法在FRA分析中特别有用。例如,对于三相变压器上的高压(High voltage,HV)绕组端到端开路试验[14],原始模型需要进行3次试验,包括高压端子组合AC、BA和CB。而对于通用的n段集总参数模型,通用高压端子指定为X-Y-Z,相应的低压(Low voltage,LV)端子指定为x-y-z。图1给出了通用X相的n段集总参数模型。

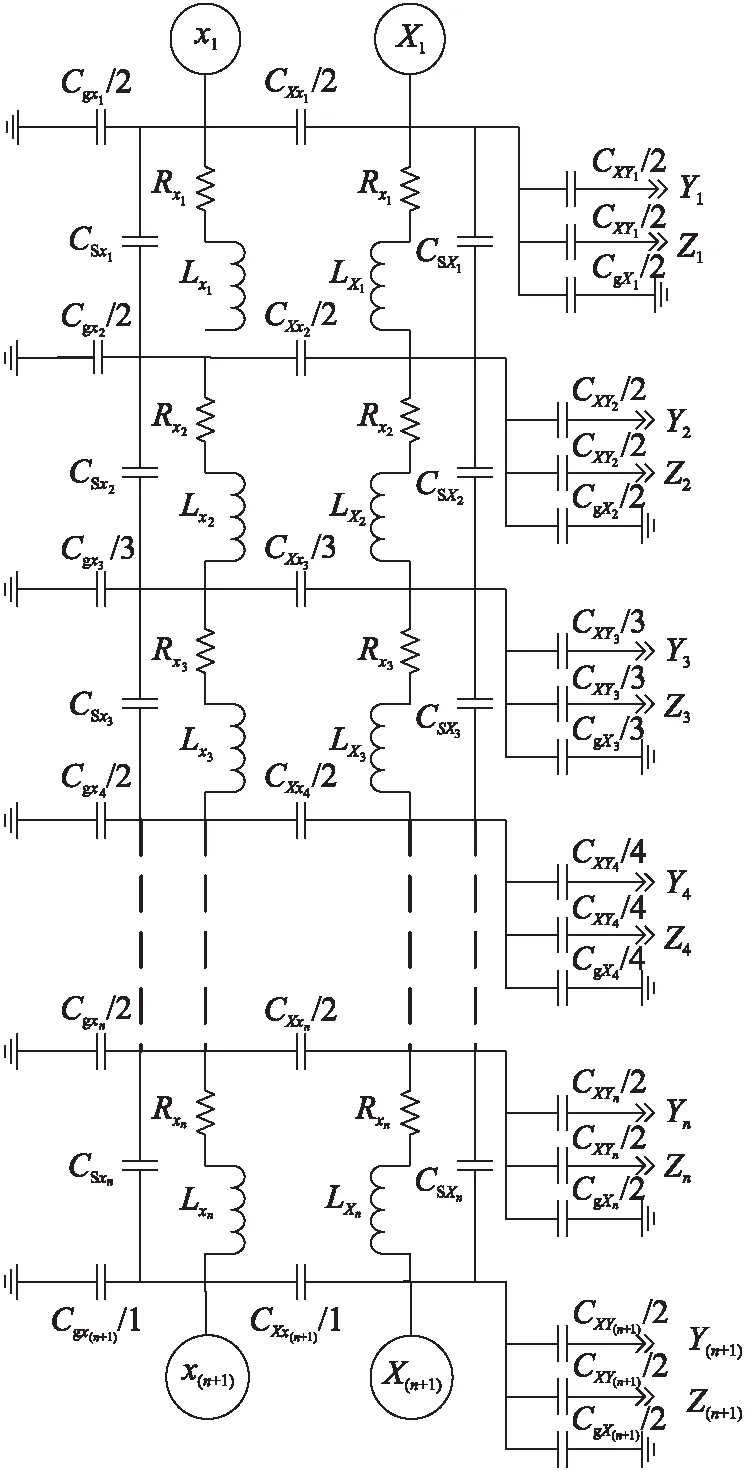
图1 通用X相变压器模型

如图1所示,高压和低压绕组由电感元件L和电阻元件R串联而成。L表示绕组的电感,与频率和由磁集肤效应造成的铁芯损耗有关。电阻元件R由绕组的直流电阻和与频率相关的趋肤效应和邻近效应构成。为了考虑绕组之间的电容,将每个等效绕组段耦合起来,用电容CXx表示。高压和低压绕组间的电容由CSX和CSx来表示。低压绕组和接地之间的电容由Cgx表示,高压绕组和变压器箱壁之间的电容由CgX表示。电容CXY和CZX表示相邻高压绕组之间的电容。将高/低绕组间的电容CSX/CSx与高/低绕组的电感LX/Lx和电阻RX/Rx并联得到的非理想电容元件来表示由电容耦合造成的介质损耗。

1.2 模型结构

通过分配适当的状态变量并考虑模型的网格电压和节点电流,可以为每个FRA测试拓扑推导出三相变压器模型的状态空间方程[15]。对模型的状态空间方程进行拉普拉斯变换,得到每个FRA测试拓扑的传递函数。这个传递函数可通过对变压器FRA进行曲线拟合来估计模型参数。这一过程可通过约束优化算法来实现,此算法可确定使成本函数最小化的模型参数值。本文所使用的成本函数如下

J=JH+JL+JHL

(1)

式中:

(2)

(3)

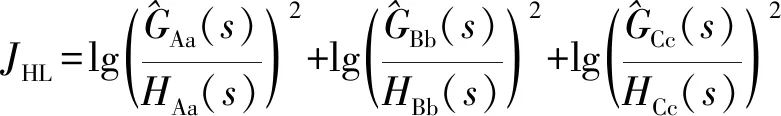
(4)

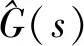
2 短路力及其潜在后果

短路会对变压器绕组和机械结构产生巨大的作用力。短路期间的漏磁场分析表明,短路力可分解为径向和轴向分量。径向漏磁主要在绕组端部,并在绕组上产生轴向力。这可能导致高压绕组相对于低压绕组发生轴向位移。沿轴向穿过铁芯窗口的漏磁将在高压绕组上产生向外的径向力,在低压绕组上产生向内的径向力。向外的径向力本质上是拉力,可拉伸导线或断开不良接头,从而导致绕组故障。导体材料抗拉强度相对较高,由于拉伸应力导致的外部绕组故障不太可能发生。然而,向内的径向力作用在低压绕组上,会导致低压绕组变形,称为径向屈曲,是常见的绕组故障。低压绕组的径向屈曲是本文研究的重点。

2.1 低压绕组的径向屈曲模态

当低压绕组的支撑结构具有比低压绕组导线本身更大的刚度时,在压缩应力下,绕组导线可能在每个垫片之间向铁芯弯曲。这称为强制屈曲[16],如图2(a)所示。低压绕组中的强制屈曲将导致高压和低压绕组之间的平均距离增加。这将导致高压到低压绕组间电容降低。相反,由于低压绕组和铁芯之间的平均距离减小,因此低压绕组到铁芯的电容也相应增加。同时,绕组变形也会影响漏感特性。

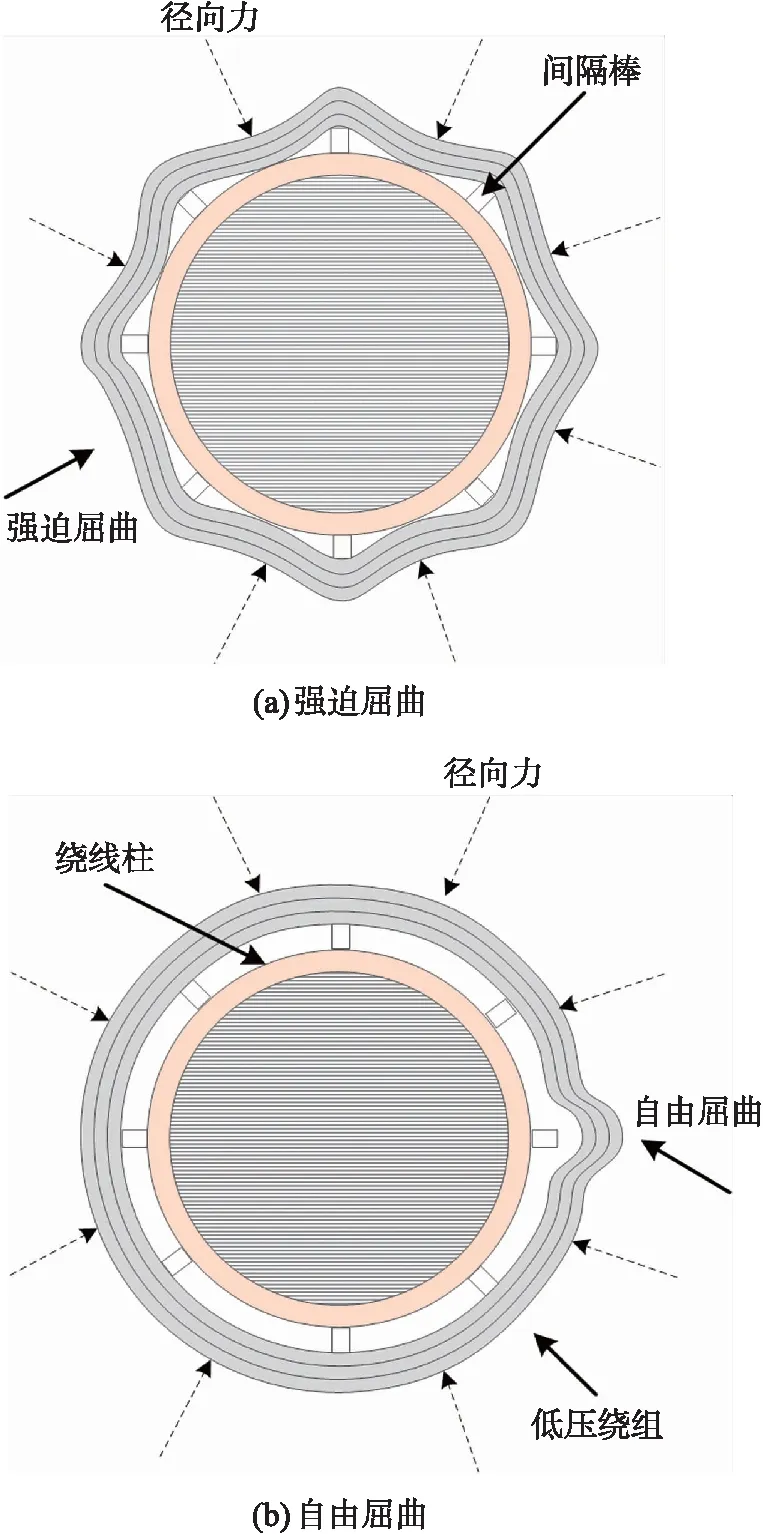
图2 与变压器低压绕组径向应力相关的屈曲模态

当导体的刚度高于绕组支撑结构时,会出现自由屈曲的屈曲模态。在这种情况下,绕组可沿圆周向内和向外弯曲[16]。此屈曲模态如图2(b)所示。

2.2 低压绕组向外径向屈曲的模拟

由于变压器的成本很高,低压绕组径向屈曲的研究是破坏性的。因此,为了获得不同绕组变形程度下的FRA数据,本文采用非破坏方法模拟低压绕组中的“屈曲”,“屈曲”本质上是暂时的,以便在测试程序结束时将变压器恢复到其原始状态。绕组屈曲会引起绕组漏感及其电容参数的变化,其中电容的变化更容易以无损方式实现。按2.1节的分析可知,模拟低压绕组屈曲引起的电容变化需要能够降低高压至低压绕组电容并增加低压绕组至铁芯电容。

变压器高压和低压绕组之间的电容可通过将其视为圆柱形电容器来估算,如图3所示。圆柱电容计算方法可参考文献[17],如式(5)所示

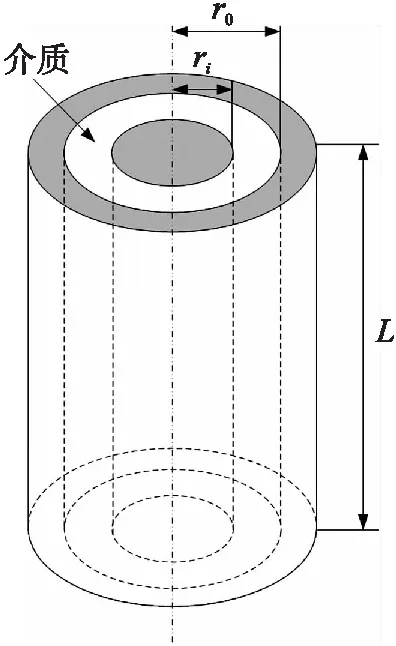
图3 圆柱形电容器

(5)

式中:ε为两个圆柱导体之间电介质的介电常数,L为圆柱长度,r0为外导体的内半径,ri为内导体的外半径,ln为自然对数。高压至低压绕组电容和低压绕组至铁芯电容均可根据式(5)的同轴圆柱关系进行估算。由式(5)可知,要想改变电容,唯一可以在不发生重大机械变化的情况下改变的参数是ε,即电介质的介电常数。ε的更改可以通过更改圆柱体之间的电介质材料来实现。

为了便于改变模拟“屈曲”所需的介电常数,在风冷变压器的高压和低压绕组之间插入了氯丁橡胶,如图4所示。由于氯丁橡胶的介电常数为6.7,通过在高压绕组与低压绕组之间插入不同数量的氯丁橡胶条便可得到不同的间隙电容,从而可以模拟低压绕组向外径不同程度的弯曲效果。尽管低压绕组中的屈曲通常向内,但本文的目的是使用FRA方法量化径向绕组的变形情况,无论变形方向是向内还是向外,此方法均适用。

图4 在高压和低压绕组之间使用氯丁橡胶嵌件模拟低压绕组中的向外径向屈曲

3 变压器“屈曲”试验

用一台1.3 MVA 11 kV/433V Dyn1风冷配电变压器进行“屈曲”试验。在A相高压和低压绕组之间插入6 mm氯丁橡胶条。如图5所示,每条氯丁橡胶条贯穿绕组的整个轴向长度。

图5 在1.3 MVA 11 kV/433 V变压器的A相上模拟屈曲

总共进行了4次“屈曲”测试。第一次测试是未作任何改变的基准测试,称为0%的“屈曲”。在第二次测试中,对变压器进行了改造,使氯丁橡胶条覆盖低压绕组外周长的8%。第三次测试的覆盖率增加到16%,第四次测试的覆盖率增加到24%。然后对每个“屈曲”样品进行高压绕组端到端开路、低压绕组端到端开路和绕组间电容的FRA试验。记录了增加“屈曲”严重程度的FRA试验结果。图6和图7分别为高压绕组端到端开路和绕组间电容的FRA试验结果。由图可以看出,与变压器A相相关的绕组的频率响应均存在明显变化。变化的程度与“屈曲”的增加程度一致。在低压绕组端到端开路FRA试验结果中也观察到类似变化。

图6 不同“屈曲”程度下高压绕组端到端开路的FRA测试结果

图7 不同“屈曲”程度下绕组间电容的FRA测试结果

4 径向“屈曲”的参数估计

如第2.2节所述,径向屈曲会导致变压器参数发生变化。为了能够描述变压器参数的变化,将变压器安装和调试后进行的FRA测试定为基准FRA,利用式(1)的成本函数在基准FRA基础上运行估算算法,以确定基准参数值。除了变形参数外,其他参数值在第一次运行后都能确定。然后使用“屈曲”变压器FRA数据重新运行估算算法。这种方法大大降低了模型自由度,使估计算法对细微参数变化更加敏感。

风冷变压器具有方便改造绕组的优点,但是它对大气温度和湿度的变化更为敏感,在一天的试验过程中,大气温度和湿度可能会发生很大变化。这会影响绝缘材料介电常数,从而影响变压器频率响应共振阻尼的变化。因此,估计的参数值会受到大气条件变化的影响。为了检测出由于“屈曲”测试而导致的模型参数的细微变化,需要将温度和湿度的影响降至最低。

Ryder[18]建议使用相间比较法来校正基准FRA。即,使用不同相间相似参数之间的差值来表征“屈曲”的严重程度。例如,检测绕组间电容之间的差值,即CAai-CBbi,其中CAai是A相高压绕组和低压绕组之间的电容,CBbi为相位B的高压和低压绕组之间的电容。将此差值作为每个“屈曲”测试的独立参数,以消除由大气条件变化引起的共模效应。表1列出了每个“屈曲”测试中各相绕组间电容估计值。由于大气变化和模型精度限制,观察到的电容变化并不总是一致的。电容值变化与“屈曲”严重程度无明显的变化规律。表2为每个“屈曲”情况下每相绕组间电容的差值。显然,当考虑A相时,绕组间电容相对于“屈曲”程度的增加而逐渐增加(列CAai-CBbi和CAai-CCci);然而,B、C相绕组间电容的差值(列CBbi-CCci)与“屈曲”严重程度就无明显关系。

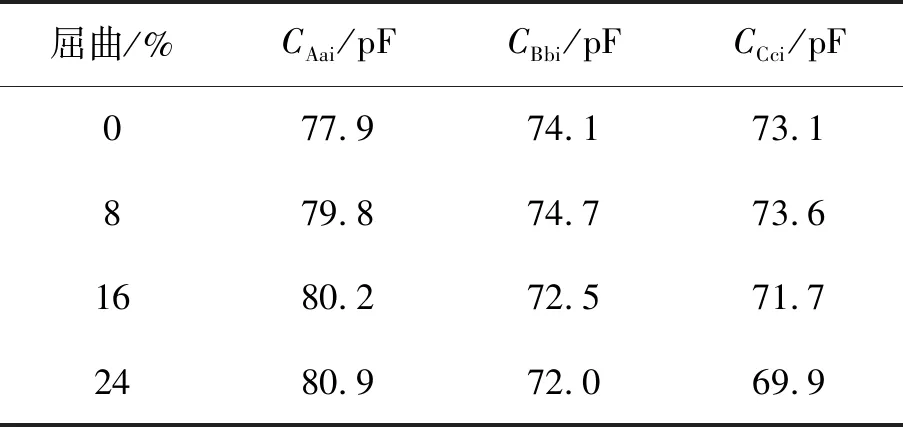
表1 各相位绕组间电容测试估计值

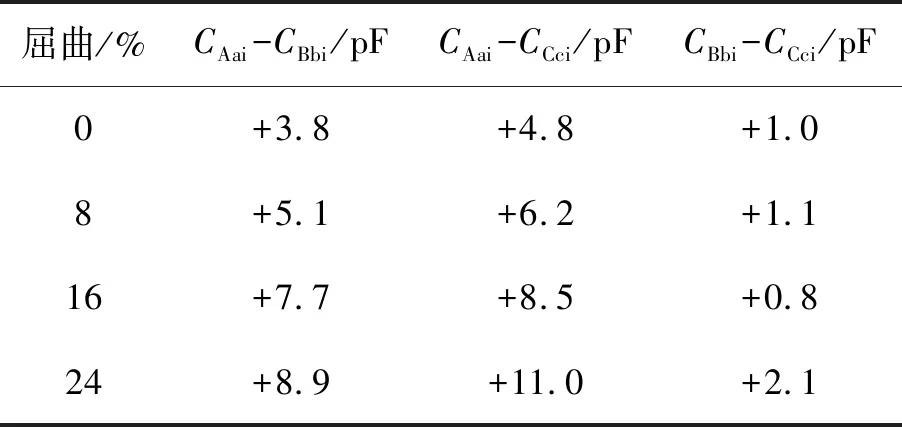
表2 “屈曲”试验绕组间电容差值

上述结果表明,A相绕组产生了绕组径向变形故障。然而,为了量化电容相对于变形的严重程度的关系,采用微分平均值来进行量化。此值也可以通过使用平均基准值作为偏移进行归一化。对于A相,可以表示为

(6)

式中:

(7)

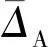
表3 不同“屈曲”程度下的绕组间电容差值(相对于A相)

为了确认绕组间电容的变化程度是正确的,将相对于基准值的变化与使用COMSOL Multiphysics软件仿真的FEA模型预测的变化进行比较。图8所示的最终FEA静电模型由代表1.3 MVA变压器高压和低压绕组(分别为红色和深蓝色)的同轴圆柱体,两个绕组之间的绝缘压板(浅蓝色),以及一个圆柱形截面、位于两个绕组之间的氯丁橡胶带(棕色)和模型电场线(红色箭头)组成。FRA计算结果与仿真结果对比如表4所示,可见,FRA计算的不同“屈曲”程度下电容值变化的百分比与FEA预测结果非常接近。