基于量子蚁群优化的近邻传播聚类算法研究

郑冬花,叶丽珠,刘月红,牛少华

(1.广州商学院 信息技术与工程学院,广东 广州 511363;2.马来西亚管理与科学大学 研究生院,雪兰莪 莎阿南 40100;3.桂林理工大学 信息科学与工程学院,广西 桂林 541006;4.北京理工大学 机电学院,北京 100081)

聚类作为无标签大数据深度分析的重要手段,占据着数据分析的重要地位。通过聚类可以有效挖掘海量数据见的隐藏联系,从而实现大规模数据的价值处理。由于聚类无先验知识辅助,其在数据挖掘过程中常常因为数据维度高或数据异构程度高而失效[1,2],无法完成数据类别划分的任务。同时,聚类的精度也常受到样本量、样本均衡程度、聚类中心数量等多种因素的制约。因此要在大规模数据中获得较好的聚类效果,必须要充分研究聚类算法,根据实际聚类需求不断改进聚类方法。

当前,关于聚类算法的研究较多,王芙银等[3]采用密度峰值算法完成聚类,并采用鲸鱼算法进行密度峰值核心参数优化,以增强聚类性能。姬强等[4]对常用深度学习算法聚类进行了详细分析,解析了常用深度学习算法应用场景并对比了其优缺点。前者对具体聚类算法进行了性能改进,后者对机器学习的算法进行比较分析,两者都对聚类性能提升瓶颈进行了说明,提出了聚类性能提升的改革方向。

近邻传播(Affinity propagation,AP)聚类算法作为一种较为新颖的聚类方法,与传统聚类方法相比,无需事先给定聚类数目,且具有更好的聚类性能和效率。近期,各种量子群体智能优化算法相继被提出,并表现出更加优秀的全局和局部寻优能力。目前,尚没有出现关于采用量子群体智能优化算法来提升近邻传播聚类性能的研究。本文采用AP聚类算法进行数据聚类,为了防止因为AP聚类算法的偏向参数设置不合理而导致聚类性能降低,引入蚁群优化(Ant colony optimization,ACO)策略,采用蚁群算法对偏向参数进行优化,并采用量子比特编码对蚁群个体位置进行编码,以提高AP聚类的适用性。

1 近邻传播聚类

设两个样本i和j的相似程度S(i,j)计算方式为[5]

S(i,j)=-‖xi-xj‖2

(1)

式中:xi和xj分别表示样本i和j的x维度函数。按照式(1)计算所有样本中任意两个样本的距离,并以矩阵输出,其对角线上的值称为偏向参数P。

在样本的相似维度函数表示中,吸引维度和隶属维度最常用,分别用r(i,j)和a(i,j)表示,将两者以矩阵形式表示,分别为R=[r(i,j)]N×N和A=[a(i,j)]N×N。

r(i,j)和a(i,j)更新方式[6]

(2)

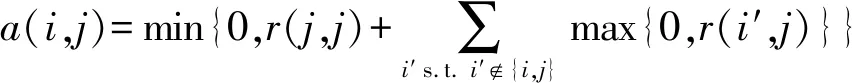
(3)

式中:r(j,j)表示j的吸引度。根据式(2),左右两边均加上a(i,j),则

r(i,j)+a(i,j)=s(i,j)+a(i,j)-

(4)

近邻传播聚类算法相似度的计算一般综合考虑r(i,j)和a(i,j),选择r(i,j)+a(i,j)的值来衡量i和j的相似程度。

令E=[e(i,j)]N×N=[r(i,j)+a(i,j)]N×N,即E=R+A,不断优化求解E而获得样本的相似度,从而完成聚类。

为了减弱R与A更新中的振荡效应,加入φ(φ∈[0,1))因子,那么T时刻的R与A计算方式为[7]

RT=(1-φ)RT+φRT-1

(5)

AT=(1-φ)AT+φAT-1

(6)

2 量子蚁群优化的近邻传播聚类

2.1 ACO算法

蚁群算法本质是通过蚂蚁路径选择来寻优。在m只蚂蚁的n个节点寻优中,通过可选节点之间的信息素来确定下个节点路径。当蚂蚁k当前处于第i个节点位置时,可选的后续节点集合为Mi,选择下一个节点的方法为[8]

(7)

式中:τ(i,s)表示Mi中节点与点i的信息素,τ0表示初始信息素,蚂蚁路径选择过程中的信息素计算采用概率方式[9]

(8)

式中:τ(i,j)是边(i,j)信息素,其系数为α;η(i,j)为启发强度,其系数为β。

蚂蚁移动到下一节点后更新信息素[10]

τ(i,j)=(1-ρ)τ(i,j)+ρτ0

(9)

式中:ρ为蒸发因子。

蚁群中蚂蚁全部路径搜索完的信息素为

τ(i,j)=(1-ρ)τ(i,j)+Δτ(i,j)

(10)

2.2 量子蚁群优化(Quantum ant colony optimi-zation,QACO)原理

量子的比特表示为[11]

|φ〉=α|0〉+β|1〉

(11)

式中:|·〉表示狄拉克符号,通常称为叠加态,α和β为非实数,|α|2+|β|2=1,|α|2和|β|2分别表示量子坍缩到“0”和“1”态的概率。

将式(11)写成矩阵方式

|φ〉=[α,β]T

(12)

令α=cos(θ),β=sin(θ),则式(12)变为

|φ〉=cos(θ)|0〉+sin(θ)|1〉=

[cos(θ),sin(θ)]T

(13)

那么对蚁群所有个体位置进行编码[12]

(14)

式中:θij=2π·Rand(),Rand()∈(0,1),i∈{1,2,…,n},j∈{1,2,…,m},n为蚁群个体总数,m表示位置维度。

设θ是[α,β]T在|0〉=[1,0]T分量上的相位,式(13)变为[13]

(15)

2.3 聚类流程

首先,将待聚类样本进行相似矩阵求解,初始化偏向参数,以偏向参数随机值建立蚁群优化算法的若干个体。然后,将蚂蚁个体位置进行量子比特化处理。接着,进行蚁群优化求解,求解适应度最高的蚁群个体,即为最佳偏向参数。在量子蚁群优化执行过程中,多个弱分类器的分类结构需要按权重投票,从而获得强分类结果,权重的设置较为关键。最后,采用最佳偏向参数AP算法完成聚类。所提QACO-AP算法的具体流程如图1所示。

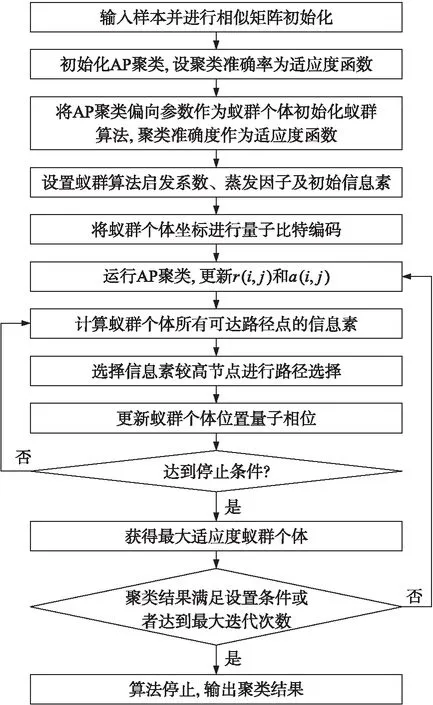
图1 基于QACO-AP的聚类流程

3 实例仿真

为了验证基于量子蚁群优化的近邻传播聚类算法,进行实例仿真,仿真数据集为公开数据集UCI,具体如表1所示。在本文的聚类性能衡量指标中,选取了常用的聚类准确度和聚类Silhouette值。仿真试验硬件参数为:CPU Inter(R)Core(TM)i7,操作系统Windows 10。

表1 仿真样本集

首先,验证ACO-AP算法采用经过优化后的偏向参数进行聚类和常用偏向参数选择方法的聚类性能差异;其次分别采用AP、ACO-AP和QACO-AP算法进行聚类性能仿真,验证量子蚁群的优化性能;最后采用常用聚类算法和QACO-AP算法进行聚类性能对比。

3.1 不同偏向参数的聚类性能

在AP聚类中,常用的偏向参数选择方法为相似矩阵的中位数和最小值两种方法,而QACO-AP的偏向参数是由QACO优化得到的,分别采用这3种偏向参数选择策略进行聚类仿真,其聚类类别数如表2所示。

表2 两种算法的聚类类别数

从表2可知,当采用P为中位数的AP聚类时,其获得聚类类别数明显大于P为最小值的AP聚类及QACO-AP聚类,这主要是因为将P设置为中位数,让更多点获得了成为类中心点的权利,所以在聚类过程中得到了多个类中心,从而造成类别数明显失真;而对于P为最小值的AP聚类,其获得的类别数也明显多于实际类别,这表明采用常规AP聚类算法对表1中样本进行聚类的适应度较差,因此引入算法对AP的偏向参数进行优化非常关键。

采用QACO-AP聚类算法时,其获得的类别数和实际类别一致,具有较强的自适应类别选择功能,这有效解决了不同样本类别数的聚类问题。下面将继续对3种偏向参数设置策略对应的AP算法的聚类准确率性能进行仿真,结果如图2所示。

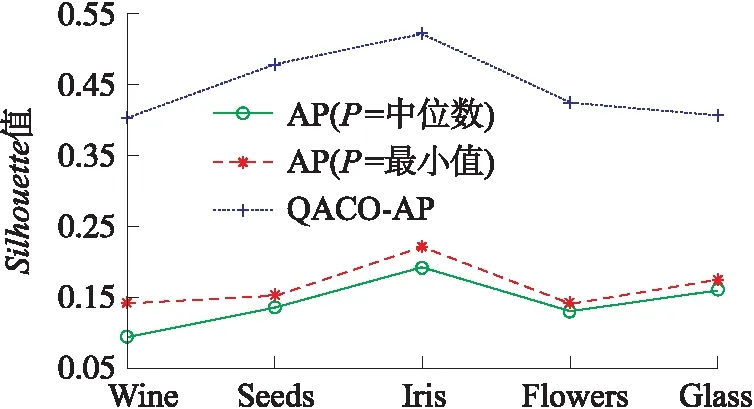
图2 不同偏向参数设置策略对应的Silhouette值

从图2可以看出,采用不同偏向参数设置策略,其对应的Silhouette值差异较大。在5类数据集中,QACO-AP算法的Silhouette明显优于未经过偏向参数优化的其他两种算法。横向对比发现,3种算法分别在Iris集获得了最高的Silhouette值。结合表2和图3知,偏向参数的设置对AP聚类的性能影响较大,在无法手动合理设置的时候,采用算法对偏向参数进行自适应优化设置是较为合适的方法。

3.2 量子蚁群的优化性能

为了进一步验证量子蚁群算法对AP聚类的优化性能,分别采用AP和QACO-AP算法对表1中的样本进行聚类仿真。

从表3可知,采用AP算法所得到的聚类类别明显大于实际类别,而QACO-AP和ACO-AP算法所获得的聚类类别明显和实际类别更接近。QACO-AP聚类获得的类别和实际类别相等,而ACO-AP在Wine和Glass数据集聚类类别和实际值一样,其他3类数据集类别与实际值不同,这表明引入ACO算法对偏向参数优化之后,聚类得到的类别数明显优于传统偏向参数确定方法。通过量子比特编码,ACO的偏向参数优化性能得到进一步提升,QACO-AP算法获得了更准确的类别数。

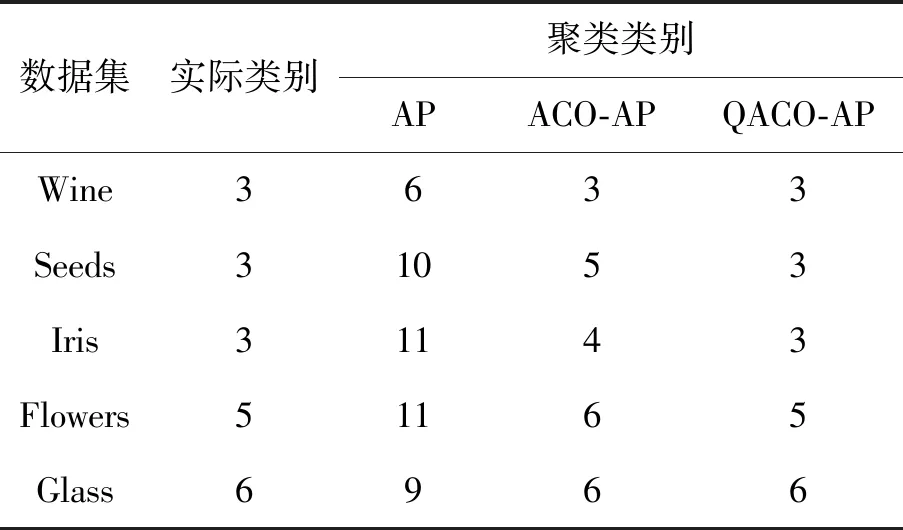
表3 3种算法的聚类类别

从图3可得,在Silhouette性能方面,QACO-AP算法均维持在0.4以上,ACO-AP算法保持在[0.3,0.36]之间,而AP算法均在0.25以下。这表明AP偏向参数经过优化之后,极大地提高了聚类的Silhouette性能,原因是QACO算法使数据集中不同簇类之间的分布更加合理。下面将继续对3种算法的聚类准确率进行性能仿真。

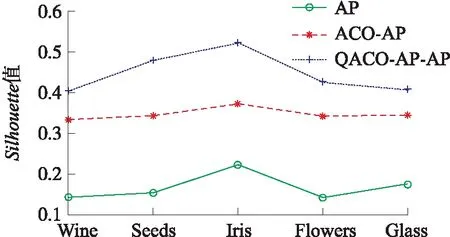
图3 3种算法的Silhouette值

从表4可知,对于5类样本集,QACO-AP的聚类准确率最高,ACO-AP次之,AP算法最差,这主要是引入偏向参数优化之后,其聚类类别更符合实际类别数,根据类间距更容易获得准确的聚类结果;从标准差角度来看,引入了QACO对AP算法进行优化之后,聚类性能更稳定了,这主要是因为当AP的偏向参数设置不合适时,由于类中心过多,容易造成聚类结果的振荡。采用QACO对偏向参数优化之后,AP聚类的类中心与实际值相同,聚类稳定性有效增强。

表4 3种算法的聚类准确率性能

从图4可得,3种算法的聚类准确率标准差性能QACO-AP算法明显优于ACO-AP和AP。从迭代次数方面来看,QACO-AP需要的迭代次数更少,ACO-AP次之,AP最多,这主要是因为在偏向参数未优化之前,AP算法需要更多次迭代来求解最高聚类准确率,而采用QACO算法优化后,获得了更优偏向参数,AP聚类效率明显提升。单从收敛曲线来看,ACO-AP和AP均有短暂陷入局部优值的情况,而QACO-AP算法标准差一直降低直至稳定。

图4 3种算法的收敛性

3.3 常用算法的聚类性能

为了进一步验证QACO-AP算法的聚类性能,将常用聚类算法决策树(Decision tree)[14]、K-中心点(K-mediods)[15]和卷积神经网络(Convolutional neural network,CNN)聚类算法[16]与本文算法进行聚类性能对比,聚类结果如图5所示。

图5 4种算法的聚类准确率

从图5可看出,对于相同的样本集,QACO-AP算法的聚类准确率最高,CNN次之,决策树最差,QACO-AP的聚类准确率优势明显。横向比较发现,4种算法均是在Seeds集上聚类准确率最高,Iris集上聚类准确率普遍较差。

4 结束语

本文采用量子蚁群优化算法对近邻传播聚类的偏向参数进行优化求解,提高了近邻传播聚类的准确性。合理设置量子蚁群优化的主要参数,能够获得较好的偏向参数优化个体,增强近邻传播聚类的适用度。仿真结果表明,相比多种常用聚类算法,QACO-AP算法的聚类准确率得到明显提升,最高可达91%,较好地避免了陷入局部优值的情况,且聚类得到的类别数明显优于传统偏向参数确定方法。下一步研究将进一步优化量子蚁群算法的核心参数,以减少量子蚁群优化的求解时间,从而提高QACO-AP的聚类效率,以应对大规模样本聚类的实时性。