机载气象雷达目标的三维建模方法研究

刘 琴， 李明磊， 汪 玲， 朱岱寅， 钱 君

(1. 南京航空航天大学， 江苏南京 211106；2. 中国航空工业集团公司雷华电子技术研究所， 江苏无锡 214063)

0 引 言

机载气象雷达的主要功能是探测飞机航路前方及左右扇形区域内的天气状况，以便帮助飞行员选择安全的航线避绕各种危险的气象区域，对保障飞行安全有着积极意义。然而，气象雷达原始数据繁冗，难以从中直接发现规律。使用先进的可视化技术能使某一时刻气象目标的分布和形态变得形象直观，将气象数据转换为易于观察的图形或图像，能够提升飞行员对复杂气象状况的快速研判能力。

近年来，地面站气象雷达数据的三维可视化技术发展迅速，许多国内外学者对此都进行了较为深入的研究。普渡大学研发了NEXRAD II级多普勒数据可视化系统，它可以处理和绘制来自多个站点的大量多普勒二级天气数据，通过对气象数据做配准融合处理后实现了云层的立体可视化。Liang等提出了一种体射线追踪方法，基于从地理坐标系中直接采集的球形体纹理，可在虚拟地球上直观地显示大气的体绘制形态。Oliveir等基于WebGL平台,在浏览器上以点云的可视化方式对气象雷达数据进行三维可视化。国内沈震宇等利用等值面生成、体绘制、质点追踪等方法，结合图形绘制技术对气象数据进行处理，实现了气象标量场和矢量场的可视化。刘岩等提出了天气雷达数据点的三维空间定位方法和任意基线雷达数据垂直剖面算法，并对移动立方体算法(Marching Cubes，MC)进行改进，实现了天气雷达数据的三维可视化系统。付则鑫等利用立方体网格算法构建三维数据场，结合MC算法实现了气象雷达数据的三维重建。毕硕本等提出了基于多层次体绘制技术，实现了气象标量数据的动态变化显示，并对传统的MC算法进行改进，得到了更精确的效果。

目前对于机载气象雷达数据三维可视化的研究较少。与地基雷达相比，机载气象雷达以飞机为运载平台，在飞行中观测更具灵活性，可以从新的视角揭示天气信息。但是机载雷达数据由于动态观测的特点，获得的气象点云噪声更加严重，俯仰观测角的范围也相对狭窄。现有技术可以从气象雷达的回波信号中恢复测量出属于冰雹和强降水云团等气象目标的三维点云区域，为进一步对气象目标进行分析提供了基础。

传统的机载气象回波数据的可视化大多局限在二维平面上，比如平面位置显示器(Plan Position Indicator，PPI)和距离高度显示器(Range Height Indicator，RHI)等，只能反映某一切面的气象分布情况。事实上，仅显示二维信息无法直观地了解机载气象目标的轮廓和空间分布情况。因此本文围绕机载毫米波雷达探测的气象目标的三维点云数据展开三维建模研究。针对气象雷达数据特征，提出了一种结合-shape和泊松重建的气象目标点云三维表面建模的方法，重建结果可直观地展示气象目标的三维空间几何形态。

1 气象目标数据三维建模技术

目前，基于等值面的重建算法常用于气象雷达数据的三维重建。等值面的生成一般采用MC算法。MC算法在进行等值面提取的时候会出现二义性问题，可能会造成重建表面上出现空洞，对气象回波数据的信息表达不够完整。并且，由于机载气象雷达数据分布不均且离散，具有远离雷达处数据采样点稀疏，靠近雷达处数据采样点密集的特点，进一步加大了气象目标三维重建的难度。为了获得清晰的气象目标表面信息，本文针对机载气象雷达数据的空间分布特征，首先利用-shape算法对气象目标点云进行初重建，以获得点云的外轮廓点；再采用主元分析法对点云进行法向量估计，获得拥有法向量信息的气象目标外轮廓点云；最后使用泊松重建算法对气象目标数据进行三维表面重构。算法流程图如图1所示。

图1 算法流程图

1.1 气象目标点云外轮廓点的获取

气象目标点云分布散乱，且包含大量冗余数据。提取其外轮廓点可以滤除异常观测点和目标结构内部的点，从而缩减点云的数量，同时突出气象目标的表面特征信息，有助于提高后续表面重建的计算速度。

-shape是从离散的空间点集抽象出其直观形状的一种方法。其本质为滚球法，主要思想是通过控制半径为的球，在点集上滚动来判断边界点，并在得到的边界点处建立三角面片，重构出整个点集的表面。其中，由于参数控制了生成多面体的精细程度，会直接影响表面重构结果，故传统方法需要多次试验调整参数的值。

为了适应不同密度的气象雷达点云数据，本文采用动态值来重建-shape表面。该算法在原本算法的基础上，以点集中点的近邻样本平均距离作为值，通过不断更新的值来判断边界点，重建出点云表面，以获取点云的外轮廓点。算法步骤如下：

1) 设输入点云为，对其建立空间索引k-D树，从中任选一点，计算其近邻平均距离，作为参数的值。在点集中搜索到距离点2内的所有点，记为点集。

2) 选取中任意两点和，根据、、三点的坐标和，计算过三点且半径为的球的球心坐标和′。

3) 在点集中除去和点后，计算其他点分别到和′的距离，若其他点到的距离均大于，或者到′的距离均大于，则表明、、是边缘轮廓点，三点构成边界三角形。反之，则表明、、不是边界点。执行下一步。

4) 选择点集中的下一组点，依照步骤2)和3)进行判断，直到遍历完点集中的所有点。

5) 选择中的下一个点，重复上述流程进行判断，直到遍历完点集中的所有点。输出点云重构表面三角形面片集合。

将气象目标点云数据作为输入，使用-shape算法，对点云数据进行三角面片化，得到点云重构表面集合，并提取点云的外轮廓点集，记为={,,…,}。

1.2 法向量估计

气象点云表面重建基于点云数据的法向量信息，其重建效果受法向量直接影响。目前，常用的点云法向量估计方法可分为以下三种：基于Delaunay三角分割法、基于鲁棒统计学方法和基于局部表面拟合法。其中，基于Delaunay三角分割法不适用于受噪声干扰的点云，基于鲁棒统计学方法以计算开销很大的表面重建为前提，计算太过于复杂。本文选择主元分析法(Principal Component Analysis，PCA)来进行气象目标点云数据的法向量估计。

PCA用局部拟合平面的方法来估算法向量，可以快速地获得表面点云的法向量信息。其主要思路是对点云中的每一个点，获得其邻域点集{,,…,}，根据总体最小二乘原理，计算出这些点所拟合的局部平面Π，其表述方程如式(1)所示。

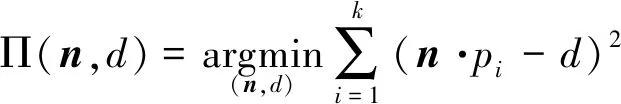
(1)

(2)

还需对法向量进行方向一致性处理，可以根据视点方向进行调整。假设视点，对于法线需满足式(3)，若不满足方程，则用-代替。

(-)·>0

(3)

输入气象目标点云外轮廓的点集合={,,…,}，利用PCA算法估计其法向量，输出记为={,,…,}，其中每个样本点都存在一个点坐标和对应法向量s.。

1.3 气象目标点云表面重建

泊松重建是一种全局优化的隐式重建算法，其输入是点云数据包含点坐标及其法向量，输出是三维网格顶点数组与三角形数组。该算法结合全局拟合和局部拟合的优点，在保证局部点云特征的同时，对点云数据进行全局性的曲面重建。基本思想是利用预估的目标模型表面的指示函数，提取点云的等值面来构建三维模型表面。

1) 离散化问题。对样本点数据集，使用样本点的位置定义八叉树ϑ，ϑ的最大深度为。给ϑ的每个节点，附加一个描述函数。设定基函数，作为盒滤波的维卷积，如式(4)所示。可以通过基函数平移缩放生成。式(5)中表示节点对应的包围盒的中心，表示节点对应的包围盒的宽度。

(,,)≡(()()())*,

(4)

(5)

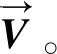
(6)

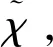
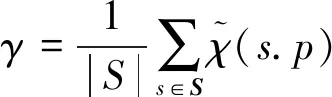
(7)

2 实验结果分析

2.1 实验说明

本文实验运行在一台配置为Intel Core i5-9300HF CPU，16G内存，win10操作系统的计算机上。实验采用的气象雷达数据是经过地杂波抑制等质量控制后，提取的气象目标点云，目标类型可以是降雨云团、雷暴云团和卷积云团等。实验采用了一组机载气象雷达实测数据、一组依据机载气象雷达扫描原理得到的气象目标仿真数据，以及三组模拟云团数据。其中，实测数据由中航工业雷达研究所研制的新一代毫米波气象雷达在载机高度6 907 m时，俯仰 [-6.03°, -9.59°]范围内扫描所得的回波数据；仿真数据是仿真参数为载机高度10 000 m，扫描方位为[-30°, 30°]，俯仰范围为[-14°, 3°]所得数据；模拟云团数据为依据气象目标点云特征所得的参照数据。

由于雷达采集到的气象数据是具有不同辐射强度的离散的空间三维点，这些点以球极坐标形式记录，建模前需先对点云数据进行坐标转换，将其转换为笛卡尔坐标。为了验证算法的有效性，本文基于Visual C++平台、QT界面框架以及计算几何算法库(Computational Geometry Algorithms Library，CGAL)对上述算法进行实现，开发了一套机载气象雷达三维目标可视化程序。图2为可视化程序界面图，其中图2(a)为一组机载气象雷达实测数据的原始点云图，图2(b)为提取的气象目标(即图2(a)中箭头所指区域)的三维建模效果图。

(a) 机载气象雷达扫描原始点云

(b) 提取的气象目标表面建模图图2 可视化程序界面

2.2 不同算法的效果比较

选用两组模拟云团数据作为数据分析源，分别用-shape算法、MC算法以及本文算法进行三维表面重建，并对3种算法效果进行分析。3种算法对云团点云数据的三维表面重建结果如图3和图4所示。表1列举了可视化处理中的数据统计，原始点云分布较为离散，利用-shape算法对云团重建结果可基本反映出云团的轮廓信息，但丢失了大量的细节区域，且生成的三角面片组成的表面为非流形(Non-manifold)表面。因而单一使用-shape算法对气象目标进行表面重建不能满足气象三维的要求，但可以看出-shape算法可以快速获取气象目标的外轮廓点；基于MC算法的云团三维重建结果对云团表面轮廓表达较为完整，重建曲面更为光滑且符合云团的概念，但表面存在部分孔洞，且运算时间较长；基于泊松重建算法生成的云团表面轮廓清晰，逼近真实表面，局部细节特征明显。

图3 3种算法的云团1重建效果

图4 3种算法的云团2重建效果

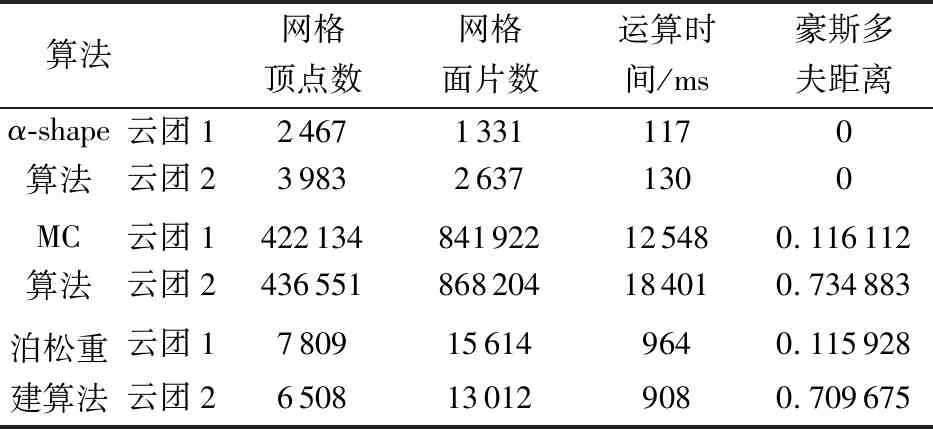
表1 3种算法实验比较结果

为了更好地分析表面重建效果的好坏，采用豪斯多夫距离(Hausdorff distance)将重建模型与原始点云之间的差异定量化。豪斯多夫距离是两组点集之间的距离度量，可以描述两组点集的相似程度。由于-shape算法是显式曲面重建，其网格顶点即为原始点云中的点，不对其进行表面模型精度分析。结合表1和图5可得，MC算法和泊松重建算法与原始点云之间的豪斯多夫距离相差不大，二者重建质量效果图中代表高质量重建结果的蓝绿色分布较为广泛，表明重建表面与原始数据的拟合程度较为理想，但也存在部分区域呈现红色或黄色，这是由于噪声干扰带来的偏差。整体来看，基于泊松重建算法得到的重建模型更为符合气象目标三维建模的要求。

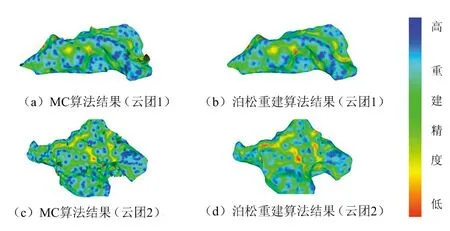
图5 基于豪斯多夫距离的云团重建误差分析

2.3 不同深度效果分析

泊松重建算法在点云数据网格化时，八叉树细分深度不同，生成的模型表面也会存在差异。实验分析了采用不同八叉树深度值对两种云团数据进行表面重建的效果差异，其中云团3为一组模拟云团数据，云团4为一组根据机载气象雷达扫描原理得到的气象目标仿真数据，重建结果如图6和图7所示。

由表2可知，当泊松重建的深度值为5时，重建模型细节特征不明显，只能显示出云团的大致轮廓，其表面网格顶点数和三角面片数较少，重建效果粗糙；当深度值为6时，云团轮廓较为清晰，重建表面开始显现局部细节特征。相较于深度值小的重建，生成表面的顶点数和三角面片数增多，运算时间也加长；当深度值为7时，云团重建表面细节特征明显，其生成网格顶点数和面片数成倍增加，重建效果好，但是也需要更长的时间完成运算；当深度值为8时，重建结果差异十分有限，且运算时间明显增加。考虑到效率问题，

图6 不同深度值云团3的泊松重建效果

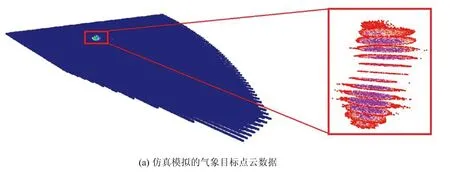
图7 不同深度值云团4的泊松重建效果

当八叉树深度为6时，云团重建效果即可满足分析需求。

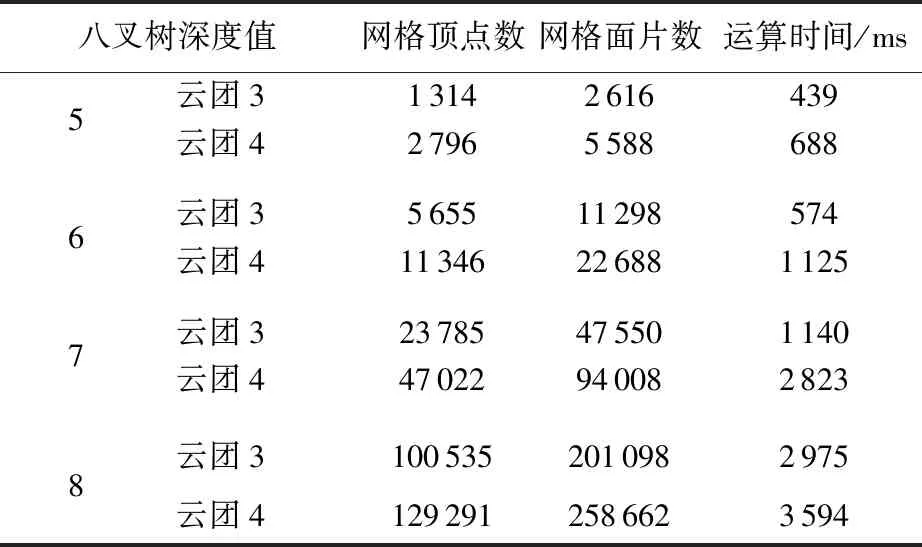
表2 泊松重建实验结果

3 结束语

本文利用-shape算法可快速准确地提取点云外轮廓点的能力，将气象目标点云作为算法的输入，获得拥有气象目标表面特征信息的外轮廓点。提出使用泊松表面建模方法对气象目标进行三维表面重建，其重建结果能清楚地反映气象目标的轮廓信息。与仅使用-shape算法和MC建模的算法进行对比，证明了本文算法对气象目标的三维表面重建的可行性。开发了气象雷达数据可视化软件，可直观、全面地展示气象目标在三维空间中的分布情况，有利于飞行员及时掌握气象目标的状态，进而达到预警和规避危险气象区域的目的。