多采场开采应力扰动与衍生灾害评价指标研究
2022-09-07池秀文陈东方汪宗英范纯超
池秀文,张 迪,陈东方,汪宗英,范纯超
(1.武汉理工大学 资源与环境工程学院,湖北 武汉,430070;2.矿物资源加工与环境湖北省重点实验室,湖北 武汉 430070;3.山东黄金矿业股份有限公司,山东 济南,250000)
0 引 言
随着易采矿山数量急剧下降,存在开采隐患的难采矿产资源逐渐成为采矿工作的重点方向,随着相邻采场的开采及应力扰动,极有可能引起一系列衍生灾害[1].近年来,一些学者对此提出了一系列解决方案,其中协同开采理论得到了广泛应用.陈庆发等[2]对协同开采理念做了大量研究,针对相邻矿体回采提出上层矿体开采仅对其上覆岩层产生影响,影响范围可通过岩层移动角圈定,并通过设置协同步距减小该影响;此外,还针对矿床开采与采空区的协同利用开展了一系列理论研究[3-5].周科平等[6-7]发明了一种将多层矿体重组为若干矿群,矿群采取统一采准,分层回采,嗣后充填的多层矿开采方法,用以减少矿层间开采时的相互影响.孙会熙等[8]以钒铁矿床为研究对象,提出了钒铁矿分区协同开采优化方案,即采用不同的采矿方法进行分区设计与分区回采,提高矿产资源回采率,降低采空区灾害发生概率.张伟等[9]研究了矿床开采过程中的采场围岩应力、位移及塑性区分布特征,开展了隐患资源开采与空区处理的协同技术研究.Kaiser P.K.[10]指出应力变化测量可以有效用于校准数值模拟出的采场围岩主应力大小及方向.李杰林等[11]将缓倾斜多层矿体的开采扰动、采空区处理、地压管理控制三者结合起来整体考虑,根据矿体赋存条件,并完成了矿群和上、下盘区矿块开采顺序的优化设计.虽然众多协同开采方法的提出对有效解决隐患资源开采的难题提供了技术支撑,但至今仍缺少对协同开采的定量化评价指标,难以评价不同开采方法的“协同程度”以及表征协同开采应力扰动与衍生灾害防空效用的定量指标.
针对多采场协同开采的评价指标及采场稳定性的研究,陈庆发教授[12]使用“协同度”评价采场协同效用,主要方法有线性加权综合法、因子分析法、理想点法和协同熵法等.Bourmas等[13]通过遗传算法训练神经网络来评估采场的稳定性.Xu等[14]提出数值模拟是研究地下采场应力变化的重要手段,采用数值模拟方法研究开挖对采场稳定性的影响.此外,陈阳等[15]针对程潮铁矿利用协同测度模型进行方案优选;赵奎等[16]使用“协同性”这一概念对下向分层胶结充填开采方法与其他采矿方法进行了对比分析;王立等[17]利用相对隶属度模型评价采空区危险性,进而对采空区进行协同前期评价.以上方法从某些方面对采场协同效用及稳定性进行了很好的定性分析.
由于在矿山开采过程中面临技术问题和采场环境存在差别,多采场协同开采评价指标或是计算繁琐,或是依赖于专家评分,应用较为困难.当前,依然缺少能够表征协同开采应力扰动与衍生灾害防控效用的定量指标.为此,针对当前协同开采理论难以有效指导隐患资源开采的问题,本文从矿体赋存条件出发,围绕开采过程中围岩应力应变规律,采用FLAC3D数值模拟[18-19]与现场监测相接合的方式,揭示了多采场开采参数和应力扰动对协同开采的作用机理,建立了能够定量描述和评价采场开采应力扰动及衍生灾害防控效应的协同开采指数.
1 协同开采指数的构建
多采场开采过程中主要产生两种危害.一是开采工作对正在开采的采场造成破坏,引起采场失稳,从而妨碍开采工作的正常进行.二是开采工作对前期已形成采空区围岩造成扰动,导致老空区失稳破坏,或造成矿区地表大规模沉陷,形成衍生灾害.多采场协同开采理念一方面确保采矿工作正常进行,达到协同开采效用;另一方面防止衍生灾害的形成,达到衍生灾害的防控效用.因此,本文构建了协同开采指数m,由协同开采效用因子m1和衍生灾害防控效用因子m2构成,用来定量描述协同开采效用和衍生灾害防控效用,如式(1)所示:
m=m1+m2
(1)
1.1 协同开采效用因子
协同开采效用评价的是开采工作顺利完成的程度,其包括两层内涵:一是开采工作是否完成,二是开采工作是否顺利.前者可用矿山实际生产矿量与计划完成矿量的比值(式2)确定,将这个比值定义为开采计划完成因子q,式中分子表示单位时间内尺寸为L×D×H的采场生产的矿石的重量.当q≥1,即实际开采矿石量不小于计划完成量时,开采完成情况好.
(2)
式中:n为单位时间采场数(个);L为采场长度(m);D为采场宽度(m);H为采场高度(m);ρ为矿石密度(kg/m3);At为单位时间矿山开采计划(t,乘以1 000换算为kg).
在满足开采指标的前提下,本采场开采后还应具备一定的稳定性,以此作为协同开采效用的另一构成要素.若采场保持稳定,其空区形成后围岩的初始应力应小于围岩强度,两者比值越小视采场越稳定.因此,构建采场初始应力状态因子pix来表示第i号采场初始应力状态(式(3)),采场初始应力状态因子为某一采场回采工作结束时围岩最大应力与围岩强度的比值.初始应力状态因子包括顶板初始应力状态因子pt、底板初始应力状态因子pf、左侧初始应力状态因子pl、右侧初始应力状态因子pr.单采场初始状态因子pi为四者之和,用式(4)表示.由式(5)可得采场总体初始应力状态因子p为各单采场初始状态因子pi的平均值.
(3)
pi=pit+pif+pil+pir
(4)
(5)
式中:σix0为第i号采场开采后的初始应力(MPa),其中顶、底板取最大拉应力,侧壁取最大压应力;σc为围岩强度(MPa).
协同开采效用因子m1可定义为采场总体初始应力状态因子p与开采计划完成因子q的比值(式(6)),m1越小,则开采工作顺利完成程度越高.
(6)
1.2 衍生灾害防控效用因子
开采导致的衍生灾害主要包括对本采场自身围岩的破坏及对矿山其他区域造成的破坏,如导致地表沉降或对邻近采场造成应力扰动.对此,使用应力扰动因子a来评价某采场开采对其他采场造成的应力扰动程度,使用塑性区比例因子b衡量开采工作对本采空区围岩破坏程度,两者构成衍生灾害防控效用因子m2:
m2=a+b
(7)
应力扰动因子即采场某处的岩石受其他采场开采扰动而产生的应力变化量与该处岩石强度的比值(式(9)),可理解为该处岩石应力向岩石强度的逼近程度.可按具体需求选取顶板应力扰动因子at、底板应力扰动因子af、左侧应力扰动因子al、右侧应力扰动因子ar使用,也可求和使用(式(10)、式(11)).为综合考虑各向主应力,使用中利用式(8)所示的相当应力计算应力扰动因子[20].
(8)
式中:σe为相当应力,MPa;σ1、σ2、σ3为主应力,MPa.
(9)
aij=aijt+aijf+aijl+aijr
(10)
(11)
式中:aijx为开采第i号采场时,对j采场的应力扰动因子,分量x=t,f,l,r分别表示顶板、底板、左侧壁和右侧壁;σij表示开采第i号当下采场时,j采场的相当应力,MPa;σ(i-1)i为开采第(i-1)号采场时,j采场的相当应力,MPa;σt为围岩抗拉强度,MPa.
塑性区比例因子为采空区围岩产生的塑性区体积与采空区体积之比(式(12)),表示开采单位体积矿体或掘进单位体积巷道对围岩产生的塑性变化区体积.
(12)
式中:VS为塑性区体积,m3;VC为采空区体积,m3.
采空区体积可通过已开采采场数量与尺寸求出,塑性区体积可通过FLAC3D内置FISH语言得到,计算过程如图1所示.首先遍历所有块单元并判断塑性区状态,随后将所有塑性区状态为真的块体体积求和,最终得到塑性区总比例因子.

图1 塑性区比例因子计算流程图 Fig.1 Flow chart of plastic zone scale factor calculation
2 采场结构参数对协同开采指数的影响分析
2.1 矿柱宽度的影响分析
利用折减后矿体及围岩物理力学参数(见表1)用FLAC3D建立数值模型,FLAC3D采用了混合-离散分区技术和显式拉格朗日算法,能求解较大范围的三维问题,常用于分析岩体、土体等连续介质渐进破坏及岩体应力场、位移场分布和变形破坏规律,在工程领域应用广泛.研究设置采场尺寸为 15 m×10 m,采场高度为 3 m,自左向右依次开采10个采场,如图2.假设矿山恰好完成开采计划,计算得到开采10个采场后的应力分布,如图3.分别计算矿柱宽度为4~10 m 的协同开采指数,为简化计算,假设恰好完成生产计划,即q为1.协同开采指数随矿柱宽度的增加而减小,即协同性逐渐增大(图4).塑性区比例因子基本稳定在1,基本不随矿柱宽度变化而变化(图5).矿柱宽度为 8 m 时,协同开采指数的变化趋势较为平缓,因此对 8 m 矿柱情形下的应力扰动因子、初始应力状态因子等进行分析.

表1 金属矿岩石参数

图2 数值模型Fig.2 Numerical model

图3 应力分布模型Fig.3 Stress distribution model

图4 协同开采指数随矿柱宽度变化曲线Fig.4 Change curve of collaborative production index with pillar width

图5 塑性区比例因子随矿柱宽度变化曲线Fig.5 Variation curve of plastic zone scale factor with pillar width
各区域初始应力因子随矿柱宽度的增加逐渐减小,但是变化幅度较小(图6).侧应力扰动因子受矿柱宽度的影响十分显著,这是由于相邻采场的开采造成上一采场右侧形成的矿柱突然承压引起(图7).在矿柱尺寸达到 8 m 后,影响逐渐平稳,这一变化趋势与协同开采指数的变化趋势相似.可见矿柱尺寸主要通过影响采场推进方向的侧壁应力扰动因子,进而影响协同开采指数.

图6 各初始应力状态因子随矿柱宽度变化曲线Fig.6 Variation curves of initial stress state factors with pillar width

图7 各应力扰动因子随矿柱宽度变化曲线Fig.7 Variation curves of stress disturbance factors with pillar width
矿柱宽度为 8 m 时,随开采进度的推进,各应力扰动因子逐渐增加,至第4个采场时达到稳定值,即开采工作的影响范围为4个采场长度.图7中右侧应力扰动因子最大,其次是顶板应力扰动因子.这是由于自左向右开采时,开采右侧采场会对左侧相邻采场的右侧壁产生较大扰动.顶板围岩受自重且悬空,自身处于易失稳状态,因此受扰动较大.相比而言,左侧壁和底板受附近开采工作的影响较小,如图8所示.
围岩各部的初始应力状态因子值不会随开采进度的推进而发生较大变化,其中顶板的初始应力状态因子值最大(图9).
2.2 采场尺寸的影响分析
将矿柱尺寸设置为8 m,采场高度不变,分别建立采场尺寸为8 m×9 m、8 m×11 m、8 m×13 m、8 m×15 m、9 m×13 m、9 m×15 m、10 m×13 m、10 m×15 m共8组数值模型,求解开采不同尺寸采场的协同开采指数.如图10,总体而言采场尺寸越大,协同开采指数越高,其中8 m×15 m的采场协同开采指数最低,即协同开采效果最好.

图8 8 m宽矿柱各应力扰动因子随开采进度变化曲线Fig.8 Variation curves of stress disturbance factors of 8 m wide pillars with mining progress
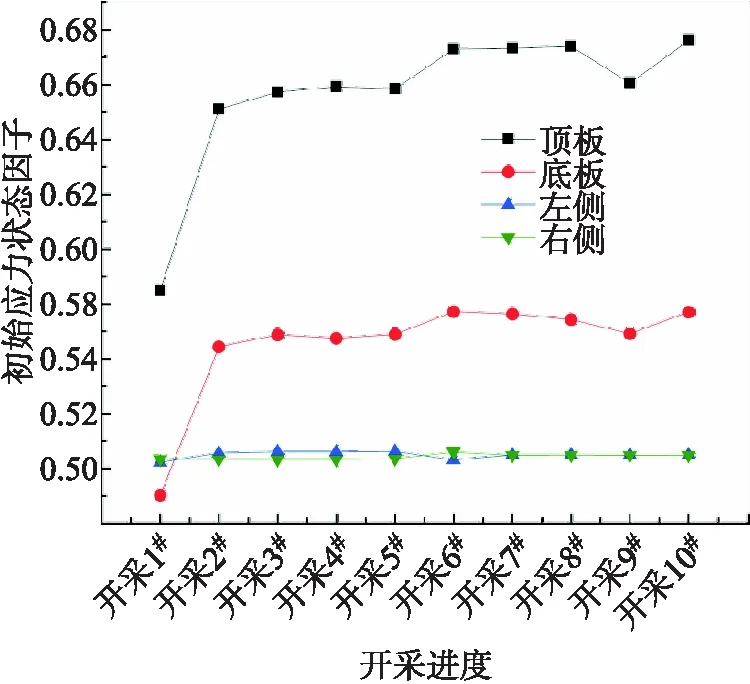
图9 8 m宽矿柱各初始应力状态因子随开采进度变化曲线Fig.9 Variation curves of initial stress state factors of 8 m wide pillars with mining progress

图10 协同开指数随采场尺寸变化曲线 Fig.10 Change curve of collaborative production index with room size
采场尺寸增加导致开采完毕后采空区暴露面积增大,因此采场顶、底板初始应力状态因子随采场尺寸变化较大且变化规律一致,采场两壁初始应力状态因子不随采场尺寸而变化,如图11所示.由此可见采场尺寸影响顶、底板初始应力状态因子进而影响协同开采指数.图中8 m×15 m采场的初始应力状态因子最小,与协同开采指数一致.
采场尺寸较小时,顶板和底板的应力扰动因子可能为负值(图12),可见小采场开采会对相邻采场顶、底板应力环境造成积极扰动.但随采场尺寸的增加,逐渐转化为消极扰动.采场跨度的增加一方面导致矿柱受力增大,另一方面也导致不相邻采场间距增大,两者对应力扰动因子的作用相反,因此扰动因子值与采场尺寸并不成正相关,图中右侧应力扰动因子远大于其他应力扰动因子.总体而言,应力扰动因子之和随采场尺寸的变大呈现出增大的趋势,但在8 m×13 m及8 m×15 m处扰动因子较小.

图11 初始应力状态因子随采场尺寸变化曲线Fig.11 Curve of initial stress state factor changing with room size
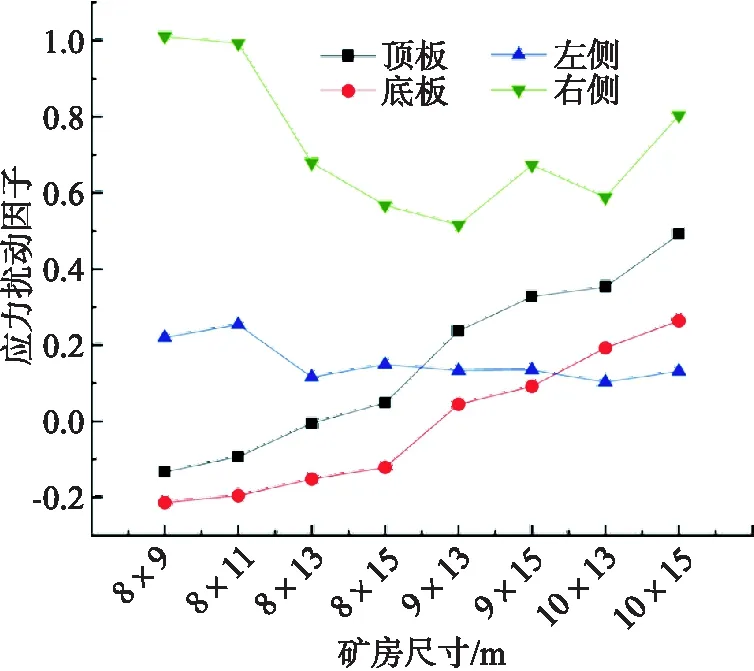
图12 应力扰动因子随采场尺寸变化曲线Fig.12 Variation curve of stress disturbance factor with room size
3 工程实例
某金属矿山在 -645 m 中段开展了一次现场试验,开采该中段的1号采场并监测采空区与巷道围岩应变.图13为实验巷道及采场布置图,矿体倾角50°,厚度 15 m,中段高度 15 m,巷道宽度 3 m.现基于这一现场试验条件进行数值模拟计算,研究协同开采指数的应用效果.
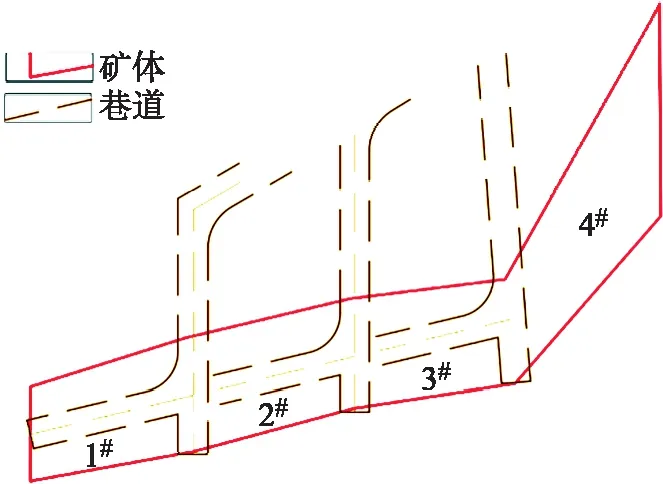
图13 某矿山-645中段1~4号采场布置图 Fig.13 Stope layout plan No.1—4 in middle section 645 of a mine
3.1 数值计算
建立如图14所示FLAC3D数值模型,利用表2中数据开展计算.初始应力平衡后,依次开挖两条穿脉巷道与1号矿房,其中巷道2紧靠1号矿房,巷道1距1号矿房较远.由于两条巷道距离较大,因此不考虑两者的开挖扰动.
如图15为1号矿房开采前后塑性区分布图,根据式(12)与图1中的的计算方法得到1号矿房开采前后塑性区比例因子分别为3.768与3.455,即塑性区体积达到了采空区体积的3~4倍,衍生灾害亟需防控,巷道与采空区应加强支护.

(a)整体模型 (b)模型内部图14 FLAC3D数值模型Fig.14 FLAC3D numerical model

表2 岩石力学参数表

(a) 1号矿房开采前 (b) 1号矿房开采后图15 塑性区分布图Fig.15 Plastic zone distribution diagram
根据上文公式计算得到采场及巷道各位置处的初始状态因子(表3)与应力扰动因子(表4).由表3可知,矿房与巷道的顶、底板应力变化幅度较大,侧帮应力变化幅度相对较小;矿房的顶、底板应力变化大于巷道顶底板,巷道两侧帮的应力变化大于矿房两侧帮.1号矿房的开采对相邻巷道扰动较大(0.021),尤其对顶板扰动最大,巷道靠近矿房的侧壁受扰动程度(0.006)远大于另一侧(0.003),与上文分析吻合.

表3 初始应力状态因子

表4 应力扰动因子
3.2 现场实验
本次试验中光纤光栅应变计通过钻孔方式埋设在回采巷道顶板及侧壁的内部(图16~图18),钻孔直径为 90 mm.

图16 矿山-645中段采场监测布置Fig.16 Mine-645 stope monitoring layout
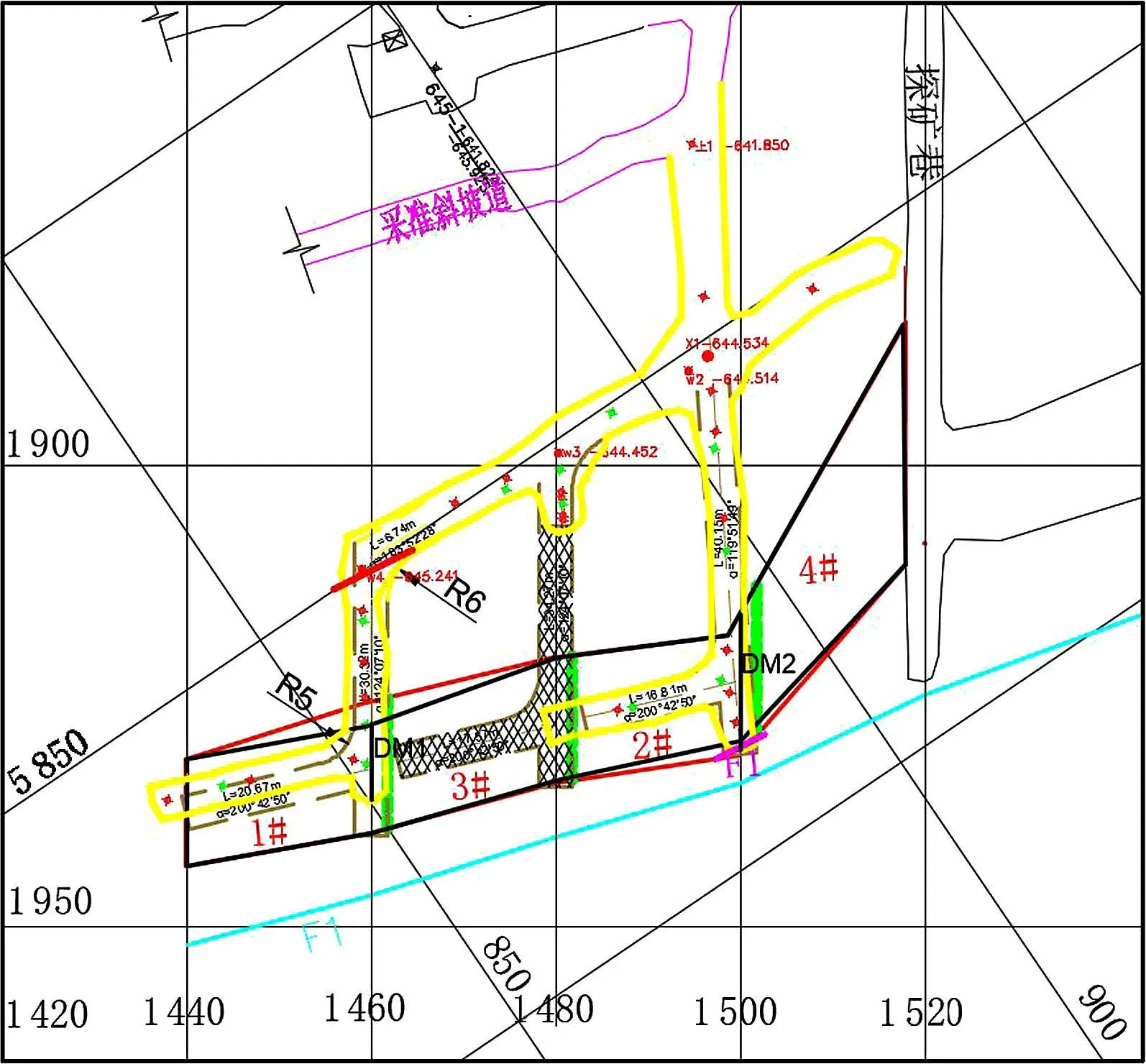
图17 现场实验Fig.17 Field experiments

图18 传感器埋设Fig.18 Sensor embedding
表5为1号矿房回采后各监测点应变值,巷道2监测点(Y1、Y2、Y3)的应变值均大于巷道1的监测点(Y4、Y5);巷道2中Y2点的应变值远大于Y3点,所得结果与数值模拟结果一致.

表5 应变
4 结 论
1)构建了协同开采效用因子与衍生灾害防控效用因子,协同开采效用因子可以表征协同开采进行情况,而由应力扰动因子与塑性区比例因子构成的衍生灾害防控效用因子,可定量描述应力扰动及围岩损伤下衍生灾害防控效用.
2)由协同开采效用因子与衍生灾害防控效用因子共同建立了开采指数,该指数越小,对于多采场协同开采越有利.
3)协同开采指数中的应力扰动因子受矿柱宽度与采场尺寸共同影响,矿柱尺寸主要通过影响采场推进方向的侧壁应力扰动因子,进而影响协同开采指数,采场尺寸主要通过影响顶、底板初始应力状态因子进而影响协同开采指数,该指数能为采场最优结构参数的确定提供一定参考.
4)运用FLAC3D对某金属矿山 -645 m 中断采场开展数值模拟,所得应力应变规律与监测结果相吻合,表明协同开采指数中的指标对于评价应力扰动与衍生灾害防控效用有一定参考意义.
