基于格的可截取签名方案*

赵 勇， 杨少军， 张福泰，3， 黄欣沂

1. 福建师范大学 计算机与网络空间安全学院， 福州 350117

2. 福建师范大学 数学与统计学院， 福州 350117

3. 福建师范大学 福建省网络安全与密码技术重点实验室， 福州 350007

4. 密码科学技术国家重点实验室， 北京 100878

5. 香港科技大学(广州) 信息枢纽 人工智能学域， 广州 511455

1 引言

数据安全对于政治安全、国防安全、经济安全和国计民生至关重要，对于解决数据泄露、数据篡改等安全问题具有重要的意义. 数字签名[1]可检测数据的真实性、完整性和不可抵赖性， 是保障数据安全的重要公钥密码技术. 数字签名的传统安全性要求是在自适应选择消息攻击下满足存在不可伪造性(existential unforgeability under adaptive chosen-message attacks， EUF-CMA)[2]. EUF-CMA 要求: 在自适应选择消息攻击下， 敌手伪造新消息有效签名的概率是可忽略的. 这虽然可以检测数据篡改， 但也阻碍了对已签名数据进行删除、合并、替换等合理操作， 不支持电子病历、电子投票等应用场景中由隐私保护带来的数据修改需求.

例如医疗信息化建设的过程中产生了大量包含姓名、药敏、治疗记录、身份证号、家庭地址等敏感数据的电子病历. 当电子病历用于医学研究或统计分析时， 需要删除可标识用户身份的敏感数据， 以保护用户的隐私. 同时， 为了保证研究结果和分析结果的有效性， 又需要向数据使用方证实删除敏感数据后电子病历的真实性. 具有EUF-CMA 性质的数字签名只能证实整份电子病历的有效性， 无法证实删除用户敏感数据后电子病历的真实有效性. 针对这个问题， 一种简单的解决办法是， 先将电子病历分为若干个数据块， 然后对每个数据块分别进行签名， 最后将所有的数据块-签名发给签名持有人. 签名持有人可以为删除敏感数据后的病历生成有效的签名， 但计算和通信的开销会随着分块的细化而增大， 不能很好地满足实际需求.

为解决上述问题， 2001 年， Steinfeld 等人[3]提出可截取签名(extraction signatures， ES)， 在不与签名人交互的情况下， 签名持有人(截取者) 可删除已签名数据中的敏感数据块， 并为截取后的数据生成有效签名. 近年来， 可截取签名在数据类型、形式化安全定义、截取规则等多个方面取得了积极的研究进展.

目前， 可截取签名方案的安全性大多基于大数分解问题、离散对数问题等传统数论困难问题. 然而， 随着近几年量子计算的快速发展， 一些传统数论困难问题在量子计算模型下可被有效求解. 例如在量子计算模型下， Shor 算法能够在多项式时间内解决经典的大整数分解问题和离散对数问题[4]. 换言之， 一旦出现足够规模的量子计算机， 基于传统数论困难问题的可截取签名将不再安全. 然而， 目前未见抗量子的可截取签名方案在主流密码期刊和会议上公开发表. 因此， 研究抗量子的可截取签名方案具有重要的理论意义和科学价值.

格密码具有抗量子、实现简单高效和平均情况/最差情况等价的安全性[5]等特点， 是最通用的后量子密码之一. 近年来， 格密码技术得到了快速的发展. 2008 年， Gentry 等人[6]提出的原像抽样函数(preimage sampleable functions， PSF) 是重要的格上密码技术， 已被广泛地应用于数字签名、IBE 等格上密码方案. 因此， 本文利用原像抽样函数， 提出基于格上小整数解问题(small integer solution， SIS) 的可截取签名方案， 在自适应选择消息攻击下满足存在不可伪造性和隐私性.

1.1 相关工作

本节介绍可截取签名和格签名的相关工作.

1.1.1 可截取签名

现有的可截取签名方案可以处理集合型数据[3，7]、树型数据[8，9]、图表型数据[10，11]等多种数据结构.可截取签名方案要满足两个基本安全要求: 不可伪造性和隐私性. 不可伪造性确保在自适应选择消息攻击下， 除依据截取规则生成已询问数据的子数据签名外， 敌手为新数据伪造有效签名的概率是可忽略的; 隐私性确保在自适应选择消息攻击下， 敌手不能在多项式时间内获取被删除的信息. 为了满足不同应用场景的需求， 可截取签名还要满足透明性[8]、不可关联性[12]、可审计性[13，14]和可合并性[15，16]等安全要求.透明性确保敌手很难判断收到的签名是原始签名还是截取后的签名.不可关联性确保敌手很难判断两个截取后的数据签名对是否来源于同一个原始数据签名对. 可审计性确保审计者可以有效地判断出数据-签名的生成人. 可合并性确保截取者可合并原始数据的截取数据组， 并为合并后的数据生成有效签名.

为了实现对可截取内容的控制， Steinfeld 等人[3]引入内容截取访问结构(content extraction access structure， CEAS)， 签名人为签名持有人指定可被截取的数据块集合， 以实现对签名持有人的截取控制.2003 年， Bull 等人[17]提出群组截取规则， 并为此提供了有效的编码方法. 2004 年， Bull 等人[18]提出实行分级群组策略的可截取签名方案， 但仅能应用于分层结构化数据. 2005 年， Miyazaki 等人[19]提出带有公开条件控制的可截取签名方案， 然而签名长度过大. 为解决这个问题， 2006 年， Miyazaki、Hanaoka 等人[20]提出基于双线性对的可截取签名方案. 随后， Ma 等人[21]引入动态粗粒度截取规则， 并提出一种安全高效的可截取签名方案. 2017 年， Ma 等人[22]提出具有细粒度单调修订控制的可截取签名方案. 2019年， Liu 等人[23]提出门限型的可截取签名方案， 限制了可删除数据块数量的阈值. 这些研究工作均丰富了可截取签名截取规则的表达力， 增强了可截取签名的实用性.

1.1.2 格签名

1997 年， Goldreich 等人[24]首次提出基于格上困难问题的数字签名方案， 即GGH 签名方案. 虽然该方案的签名和验证算法都比较高效， 但没有严格的安全性证明. 2001 年， Hoffstein 等人[25]提出基于NTRU 格的签名方案， 即NSS 签名方案. 2003 年， Hoffstein 等人[26]设计出一种更加高效的格上签名方案， 即NTRUSign 签名方案. 但Gentry 等人[27，28]证明了NSS 签名方案及其变形均可被攻破， 并指出GGH 签名方案和NTRUSign 签名方案均存在安全漏洞. 2006 年， Nguyen 等人[29]提供了一种可以攻破GGH 签名方案的方法. 随后， 分别在随机谕言器模型和标准模型下可证明安全的格上签名方案受到了高度关注.

随机谕言器模型下的格签名. 2008 年， Gentry 等人[6]改进格上抽样技术， 设计了一种单向陷门函数，并提出可证明安全的格上签名方案. 2012 年， Lyubashevsky[30]基于Fiat-Shamir 转换， 提出无陷门的格上签名方案. 2013 年， Ducas 等人[31]利用双峰高斯， 设计出安全高效的BLISS 签名方案. 2014 年， Bai等人[32]优化压缩技术， 缩短了签名的长度.

标准模型下的格签名. 2008 年， Lyubashevsky 等人[33]提出可证明安全的格上签名方案， 但仅是一次签名方案. 2010 年， Cash 等人[34]借助单向陷门函数， 以及格基委派技术， 提出了可证明安全的格上签名方案. 2012 年， Micciancio 等人[35]改进格基陷门生成算法， 并提出一种高效的格上签名方案. 2014 年，Ducas 等人[36]构造出理想格中的数字签名方案， 缩短了公钥长度. 2016 年， Zhang 等人[37]实现了格上可编程哈希函数， 并提出一种可证明安全的短签名方案.

近年来， 在美国国家标准与技术研究院征集的后量子密码方案中， 格上密码方案最多. 在第三轮入围的数字签名中， 格上签名方案独占两席， 即Dilithium[38]和Falcon[39]. Falcon 的密钥较短， Dilithium具有较高的计算效率. 这两类格上签名方案代表了格签名的发展方向.

2 预备知识

本节首先给出相关符号说明， 其次介绍关于格密码的基本概念及其相关基础知识.

2.1 符号

数据M由N个数据块组成， 表示为M={M[1]，M[2]，···，M[N]}， 其中M[i] 表示M中第i个数据块; 另外， 用CI(M) 表示M中非空数据块对应的索引集合.

表1 数据M 与索引集CI(M)Table 1 Data M and index set CI(M)

2.2 格

格是定义在Rm上的离散加法子群. 下面给出格的定义.

定义1 给定Rm中一组线性无关的向量B={b1，b2，···，bn}， 则由B生成的格Λ 定义如下:

2.3 可截取签名

可截取签名允许签名持有人(截取者)在不与签名人交互的情况下对已签名的数据进行删除截取操作，并为截取后的数据独立计算有效的签名.

定义4[3]可截取签名方案(extraction signatures， ES) 由下面四个多项式时间算法构成:

(1) ESGK(k): 输入安全参数k， 输出公私钥对(pk， sk). 记作

(3) ESExt(M，pk，X，σ): 输入数据M， 公钥pk， 待截取子集X ⊆[N] 和可截取签名σ， 输出被截取的数据签名对(M′，σE)， 其中CI(M′)=X. 记作

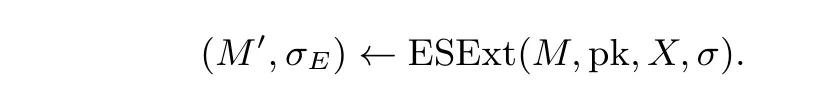
(4) ESVer(pk，M，σ): 输入公钥pk， 数据M和签名σ. 输出验证结果“1” 或“0”， 其中“1” 表示签名σ有效， “0” 表示签名σ无效. 记作

可截取签名方案的正确性. 对任意数据M和(pk，sk)←ESGK(k)， 有

· ESVer(pk，M，ESSig(M，sk))=1.

· ESVer(pk，ESExt(M，pk，X，ESSig(M，sk)))=1.

可截取签名方案的安全性. 可截取签名方案ES 的两个基本安全要求是不可伪造性和隐私性.

可截取签名方案的不可伪造性要求， 在自适应选择消息攻击下， 敌手不能在多项式时间内伪造出新数据的有效签名. 该安全性通过敌手A与挑战者C之间的交互实验ESUFExpA，ES(k) 定义:

(1) 挑战者C运行密钥生成算法， 获取公私钥对(pk， sk)， 并将公钥pk 发送给敌手A.

(2) 敌手A适应性地选取q个数据{M1，M2，···，Mq}询问签名谕言器， 得到q个原始签名. 令Q={M1，M2，···，Mq}.

(3) 敌手A输出伪造的数据签名对(M*，σ*E).

(4) 挑战者C运行验证算法， 得到b= ESVer(pk，M*，σ*E). 如果b= 1， 且∀M ∈Q，M*⊈M， 则敌手A伪造成功， 并返回“1”; 否则敌手A失败， 并返回“0”.

定义5 如果对于所有的PPT 敌手A， 存在可忽略函数negl 满足:

则称可截取签名方案ES 在自适应选择消息攻击下满足存在不可伪造性.

可截取签名方案的隐私性要求， 在自适应选择消息攻击下， 攻击者不能在多项式时间内获取到已被删除的信息. 该安全性通过敌手A与挑战者C之间的交互实验ESPRExpA，ES(k) 定义:

则称可截取签名方案ES 在自适应选择消息攻击下满足隐私性要求.

3 基于格的可截取签名方案

本节结合可截取签名方案的定义[1]， 利用格上原像抽样函数， 构造基于格上小整数解问题的可截取签名方案， 并给出此方案的正确性分析和安全性证明.

3.1 方案设计

基于格的可截取签名方案由以下五个算法构成:

(1) Setup(k): 输入安全参数k， 选取正整数n，q ≥2， 维数m=O(nlogq). 输出参数组params =(n，q，m).

3.2 正确性分析

3.3 安全性证明

证明: 假设存在敌手AES能以不可忽略的概率攻破上述可截取签名方案的不可伪造性. 现构造算法S模拟攻击环境， 具体过程如下:

4 实验结果

本节介绍本文方案的实验结果. 实验主要测试密钥生成算法、签名算法和截取签名算法的运行时间，以表明本文方案的实用性. 另外， 在本文实验给定的参数设置下， 给出本文方案相应的比特安全性.

本文方案的实现在Intel® Xeon(R) Gold 6248 CPU @ 2.50 GHz×80 的服务器上进行. 借助Sage-Math 编译器的良好性能， 配置并调用多个外部库(如PyCryptodome、FPYLLL 等)， 充分提高了方案的实现效率.

在签名算法的实现方面， 基于文献[31] 中优化的离散高斯抽样算法， 实现原像抽样算法. 此外， 由于本文方案是基于G-陷门构造的， 原像抽样算法的输入基矩阵是稀疏的， 有效地简化了抽样算法， 从而改良了签名算法的性能. 除了对签名算法的分析， 实验还分析并测试了截取签名算法的有效性. 在实验中， 分别截取原始数据的50%、25%、12.5%， 作为截取签名算法的输入， 以检测在不同的截取需求下截取签名算法的有效性与实用性. 实验结果如表2 所示.

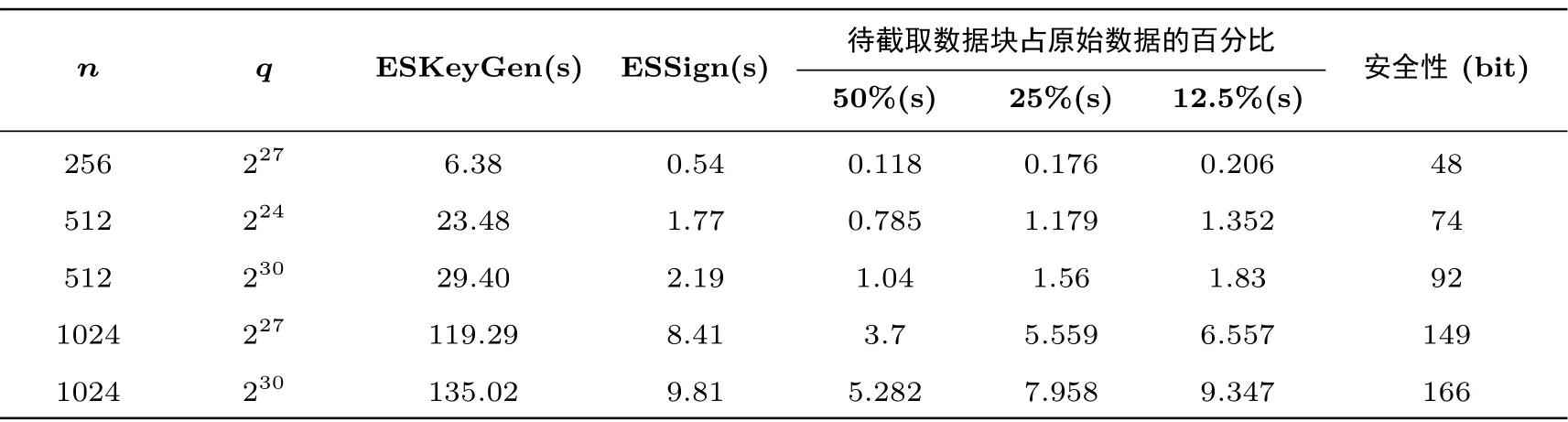
表2 实验数据Table 2 Experimental data

表2 中的实验数据表明， 随着n变大， 签名算法所耗时间也随之增加. 另外， 在不同的截取比例下， 实验检测了截取签名算法的有效性， 更有力地表明截取签名算法的实用性. 正如图1 所示， 截取签名算法所耗时间与待截取的数据块数量成反比， 能够大批量地处理实际的截取需求. 综上所述， 在达到较高比特安全性的同时， 本文方案的效率较高， 接近实际应用的要求.

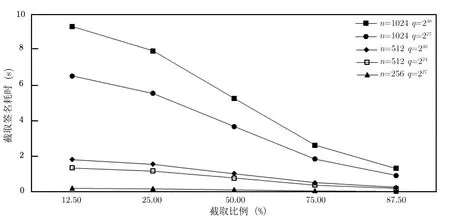
图1 截取签名算法的效率与截取比例之间的关系Figure 1 Relationship between efficiency of extraction signature algorithm and extraction ratio

值得注意的是， 若在本文方案的原始签名中加入信息〈c[i]〉i∈[N]， 则可在不影响方案安全性的情况下，就去除截取签名算法中耗时的矩阵向量乘法， 而只需对原始的数据签名对执行简单的删除操作. 此时， 截取签名算法的效率将是微秒级. 因此， 如果不考虑原始的签名长度， 本文方案的截取签名算法将会得到极大的优化.

5 总结与展望

本文提出一个基于格上小整数解问题的可截取签名方案， 并证明了该方案在适应性选择消息攻击下具有不可伪造性和隐私性. 在不同的参数设置下， 本文从理论上分析了该方案对应的比特安全性. 实验结果表明， 本文方案在达到较高安全强度的同时， 具有较好的效率， 为进一步研究格上的可截取签名方案打下了良好的基础. 此后， 基于格上的其他困难问题， 研究者可尝试设计更加安全高效的可截取签名方案. 另外， 为进一步实现对数据的有效控制， 研究者可结合已有的一些截取控制规则构造出更具实用性的格上可截取签名方案.