AES 和PRINCE 的6 轮混合差分攻击*

谭 林， 闫雪萍， 戚文峰

战略支援部队信息工程大学， 郑州 450001

1 引言

高级加密标准AES[1]是目前使用最多、研究最多的分组密码算法. 许多密码算法、Hash 函数和伪随机数发生器采用类似AES 的结构来设计， 甚至直接采用减轮AES 作为核心部件. 从AES 提出至今二十多年来， 学者们进行了大量密码分析研究. 虽然未对AES 产生实际的威胁， 但学术界持续的研究促进了人们对AES 密码结构性质的认识和AES 型密码分析技术的发展. 对AES 主要的密码分析技术有: 积分[1，2]、不可能差分[3-6]、零相关线性[7-10]、子空间路径[11]、混合差分[12-16]、yoyo[17]、交换攻击[18]、飞镖[19]、中间相遇攻击[20]等. 2016 年以前， 针对AES 的区分攻击最多只到4 轮， 包括经典的积分、不可能差分和零相关线性等. 利用AES 列混合矩阵的特点， 文献[9，10，21] 给出了密钥相关的5 轮区分器.在2017 年欧密会上， Grassi 等人[16]发现了5 轮AES 具有“8 的倍数” 结构性差分特征， 首次给出了5轮AES 与密钥独立的区分器. 文献[22] 给出了“8 的倍数” 结构性差分特征的一般化证明. 该特征揭示了5 轮AES 具有结构性的不随机性， 基于此， 文献[12] 提出了针对AES 的混合差分分析. 在2017 年亚密会上， Rønjom 等人[17]将yoyo 技术应用于SPN 型密码分析， 给出了首个与密钥独立的6 轮AES区分器. Yoyo 技术与混合差分具有很强的关联性， 文献[23] 指出了AES 的4 轮yoyo 区分器等价于广义混合差分区分器. 文献[14，15] 利用混合差分技术给出了减轮AES 的具有实际数据和存储复杂度的攻击方案. 其中， 5 轮AES-128 的混合差分攻击的复杂度为224， 这是目前选择明文模式下5 轮AES 密钥恢复攻击的最好结果. 在2019 年亚密会上， Bardeh 等人[18]将混合差分、yoyo 等技术与概率分析方法相结合， 给出了首个选择明文模式下的6 轮AES 区分器， 这是目前为止对AES 区分分析的最好结果. 在2020 年欧密会上， Dunkelman 等人[19]基于混合差分技术提出“折回镖” 攻击， 给出了适应性选择明密文模式下5 轮AES 密钥恢复攻击的最好结果. 本文在文献[14，15] 的基础上， 适当地提升数据和存储复杂度， 改进了6 轮AES 混合差分攻击的时间复杂度， 使得总复杂度为262.62. 在本文中， 总复杂度是指数据复杂度、时间复杂度和存储复杂度的最大值. 表1 给出了目前5 轮以上AES-128 密钥恢复攻击的主要结果， 数据复杂度中ACC 表示适应性选择明密文， 其余是选择明文.

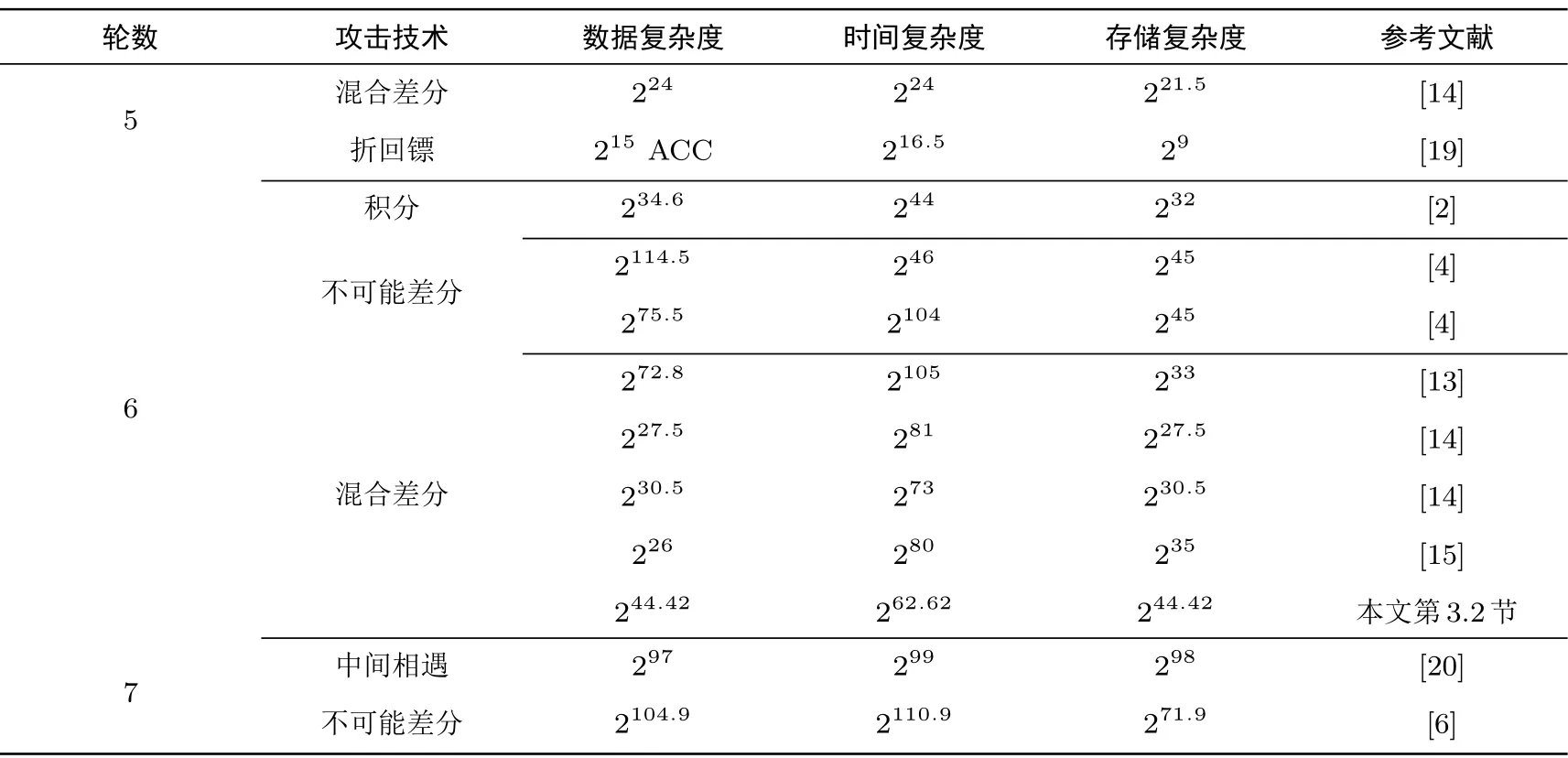
表1 5 轮以上AES-128 密钥恢复攻击主要结果Table 1 Key recovery attacks on 5 and more rounds of AES-128

PRINCE[24]是Borghoff等在2012 年亚密会上提出的一种AES-like 低时延轻量级分组算法， 适用于物联网环境下的加密. 它基于FX 结构设计， 采用α反射技术， 加解密具有对称性， 在硬件实现上具有优势. 2014 年PRINCE 的设计者发起了针对该算法实际攻击的公开挑战， 使其成为研究的热点.对PRINCE 主要的密码分析技术有: 积分[25-27]、差分[28，29]、截断差分[26，30]、多重差分[23，31]、高阶差分[25]、中间相遇[28，32]等. 目前， PRINCE 的密钥恢复攻击最长的是10 轮多重差分攻击[31]和10 轮中间相遇攻击[28，32]. 由于PRINCE 具有AES-like 结构， 针对AES 的许多分析技术可以直接应用于PRINCE 和PRINCEcore的分析. 文献[23] 将混合差分攻击技术应用于PRINCE， 给出了5 轮PRINCEcore的混合差分密钥恢复攻击. 本文将改进的6 轮AES 混合差分攻击应用到6 轮的PRINCE和PRINCEcore， 给出了总复杂度分别为230.66和222的密钥恢复攻击， 其中6 轮PRINCEcore的攻击结果优于积分攻击和差分攻击. 表2 给出了目前6 轮以上PRINCE 和PRINCEcore的密钥恢复攻击的主要结果.

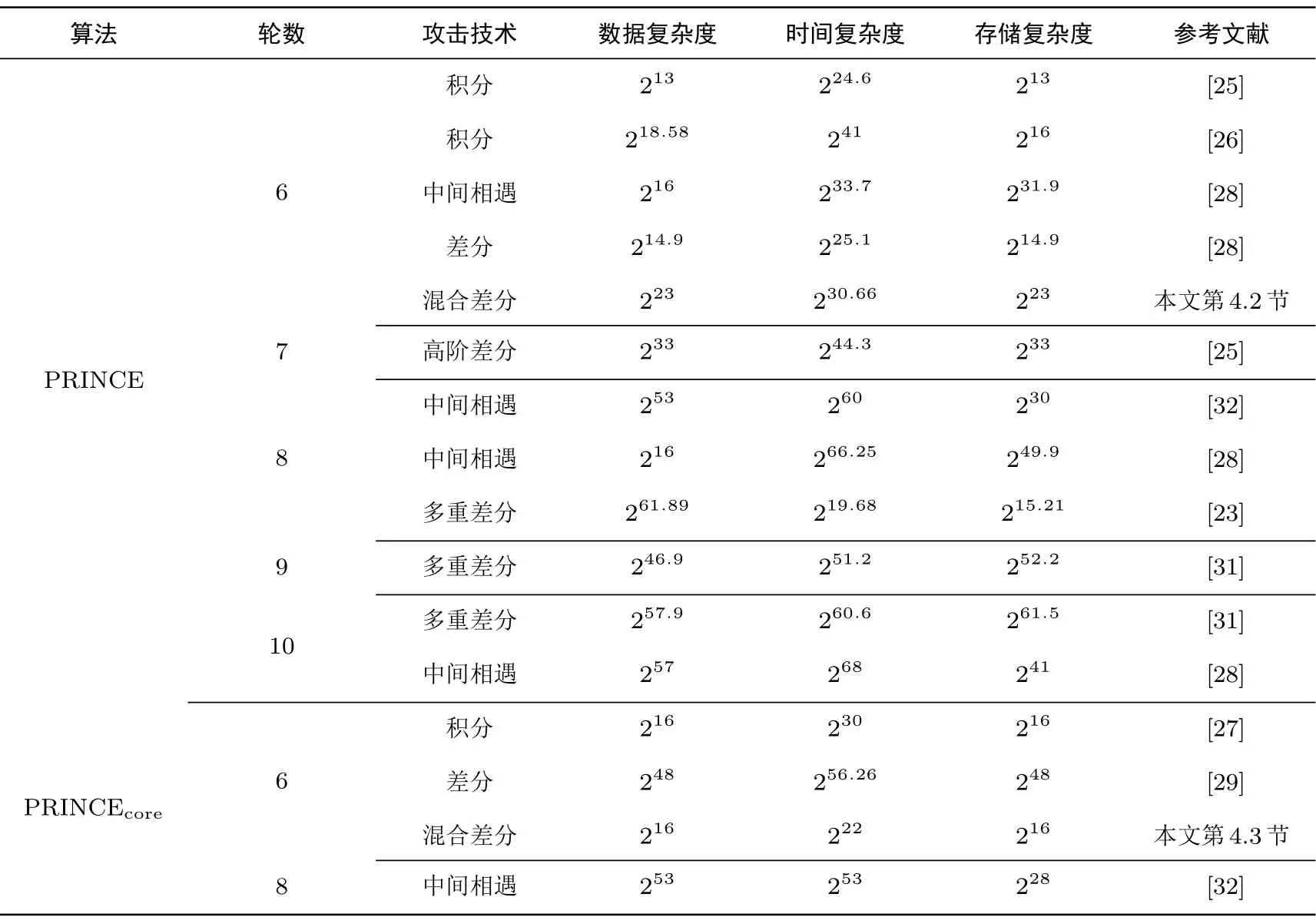
表2 6 轮以上PRINCE 和PRINCEcore 密钥恢复攻击主要结果Table 2 Key recovery attacks on 6 and more rounds of PRINCE and PRINCEcore

2 准备工作

在AES 和PRINCE 算法中， 通常将明文、密文、轮密钥以及中间状态用4×4 的矩阵来描述， 元素顺序如图1 所示. 记col(i) 表示矩阵的第i列， SR(col(i)) 表示矩阵的第i条反对角线， SR-1(col(i))表示矩阵的第i条对角线，i= 0，1，2，3. 对矩阵X， 记X{i1，i2，···，in}表示X的第i1，i2，···，in个元素，Xcol(i1，i2，···，in)表示X的第i1，i2，···，in列.X的对角线和反对角线采用相似的方式表示.

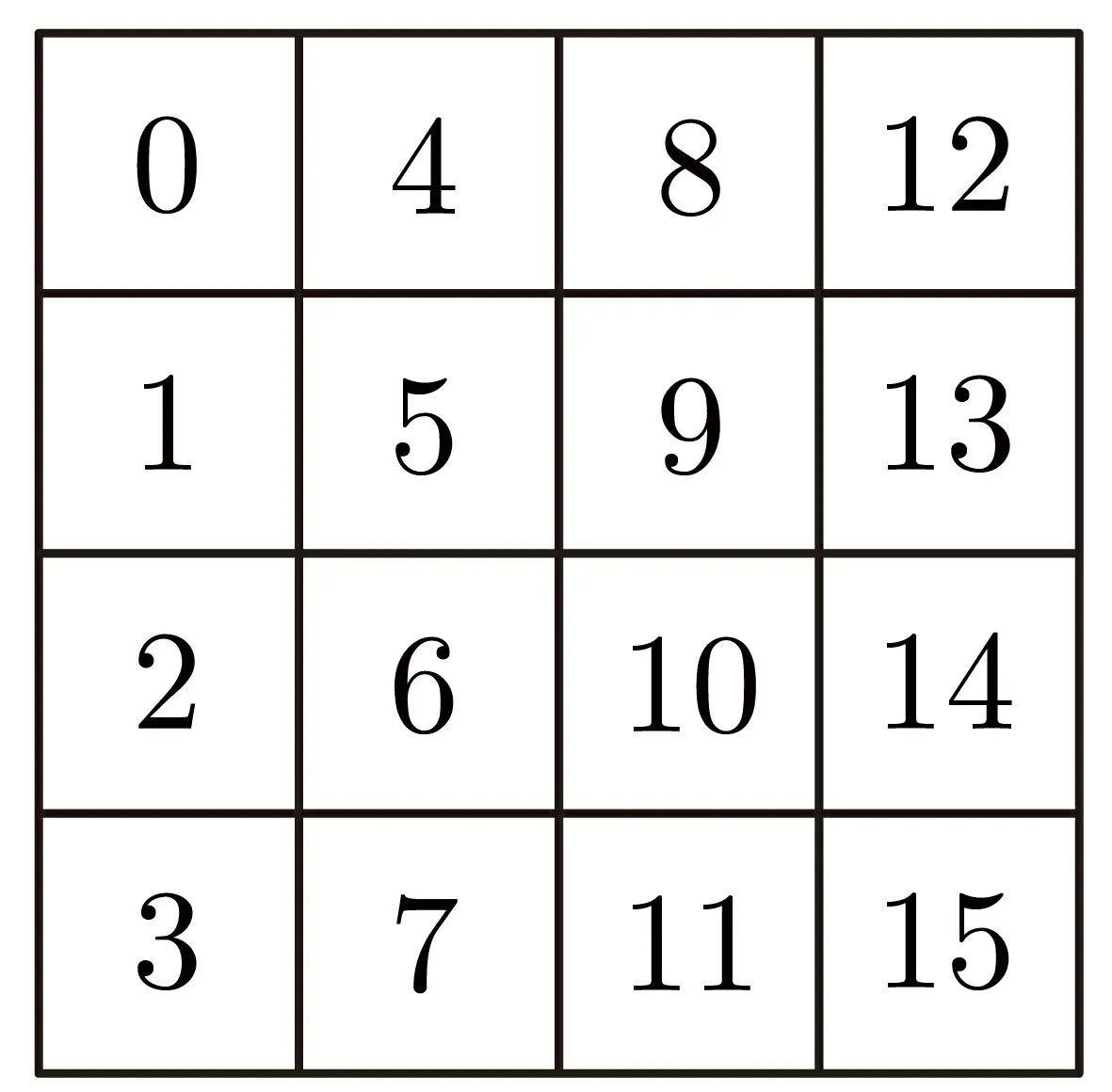
图1 状态矩阵元素顺序Figure 1 Order of elements in state matrix

文献[12] 提出了明文混合结构的概念并应用于减轮AES 的混合差分分析， 文献[15] 给出了混合结构和混合四元组更一般的定义.

定义 1[15]设X1，X2，X3，X4是四个4×4 的矩阵， 它们仅在第j列的值不同， 0≤ j ≤3.

3 AES 的6 轮混合差分攻击

3.1 AES 简介与4 轮混合差分区分器

AES 算法的分组长度为128 比特， 密钥长度支持128、192 和256 比特， 相应的迭代轮数分别为10、12 和14， 分别用AES-128、AES-192 和AES-256 来表示. 轮变换包括以下4 个操作:

- 字节替换(SB): 状态矩阵的每个字节查询同一个8 比特的S 盒.

- 行移位(SR): 将状态矩阵的第i行循环左移i个字节， 其中i=0，1，2，3.

- 列混合(MC): 用F28上一个MDS 矩阵乘以状态矩阵的每一列.

- 轮密钥加(AK): 将状态与轮密钥逐比特异或.

AES 算法中明文先与主密钥异或，再进行相应的轮变换，最后一轮没有MC.关于AES 详细的介绍参见文献[1]. 记Kr表示第r轮轮密钥，它由主密钥K0通过密钥扩展算法产生. 记R=AK°MC°SR°SB表示AES 的轮函数， 和绝大多数文献一样， 用Rn表示n轮AES， 最后一轮没有MC. 本文的研究对象是6 轮AES-128.

在文献[12] 中， Grassi 发现了明文混合结构经过4 轮AES 后保持差分的某种关联性， 由此构造了4轮混合差分区分器.

定理1[12]设(X1，X2，X3，X4)是AES 算法中一个混合四元组，则(R4(X1)+R4(X2))SR(col(i))=0当且仅当(R4(X3)+R4(X4))SR(col(i))=0，i ∈{0，1，2，3}.

在4 轮AES 混合差分区分器的基础上往前增加一轮， 文献[16] 给出了首个与密钥独立的5 轮AES区分器“8 的倍数”. 选择第0 条对角线遍历、其余12 字节取任意固定值的232个明文， 经过1 轮后状态仅在第一列活跃. 对任意的状态对(X1，X2)， 存在8n-1 个对(X3，X4) 与其构成混合四元组， 所以密文差分在任意反对角线为0 的密文对个数是8 的倍数. 文献[12] 基于4 轮AES 的混合差分区分器给出了5 轮密钥恢复攻击， 其猜测K0的某条对角线， 在第一轮MC 后构造混合四元组， 利用定理1 来判断猜测密钥的正确性， 恢复全部密钥的复杂度为234. Bar-On 等人[14，15]利用更少的混合结构和预处理表等技术进一步改进了5 轮AES 的混合差分攻击， 总复杂度为224. 在5 轮混合差分攻击的基础上往后增加一轮， Bar-On 等也给出了具有实际数据和存储复杂度的6 轮混合差分攻击， 数据、存储复杂度均为230.5，时间复杂度为273. 本节在文献[14，15] 的基础上， 适当地提升数据和存储复杂度， 改进了6 轮AES 混合差分攻击的时间复杂度， 使得总复杂度为262.62.

3.2 改进6 轮AES 混合差分攻击的时间复杂度

交换第5 轮的AK 和MC， 用等效的轮密钥加AK′来表示， 6 轮AES 加密过程如图2 所示. 记第1轮MC 后的状态为X， 第5 轮MC 后的状态为W，Z=MC-1(W). 我们选择第0 条对角线遍历、其余12 字节取任意固定值的明文结构， 每个结构约有263个明文对. 猜测K0的第0 条对角线K0，SR-1(col(0))，在状态X处构造混合四元组(X1，X2，X3，X4). 由于AK 操作不改变混合结构关系， 由定理1， 如果存在某个i ∈{0，1，2，3}使得(Z1+Z2)SR(col(i))= 0， 则(Z3+Z4)SR(col(i))= 0. 猜测第6 轮部分轮密钥， 解密至状态Z， 利用4 轮区分器对猜测密钥进行筛选. 文献[15] 称满足存在i ∈{0，1，2，3}使得(Z1+Z2)SR(col(i))=0 的明文对(P1，P2) 为Good Pair. 筛选密钥需要至少有一对Good Pair， 平均意义下找到一个Good Pair 的概率为4×2-32=2-30， 所以每次密钥猜测需要对至少230个明文对进行部分加密和解密. 我们对密文对施加限制条件来提高找到Good Pair 的概率. 选择密文差分有两条反对角线为0 的密文对(C1，C2)， 例如(C1+C2)SR(col(2，3))=0， 则(Z1+Z2)col(2，3)=0， 从而Good Pair 存在的概率为2-16×4 = 2-14. 这样， 对每次密钥猜测所要进行操作的数据对从230降低到214， 改进了筛选密钥的计算复杂度， 付出的代价是为了找到满足密文差分条件的密文对需要增加数据复杂度. 为获得满足条件的214个数据对， 需要215个明文结构. 下面详细介绍我们6 轮AES 混合差分攻击的流程.

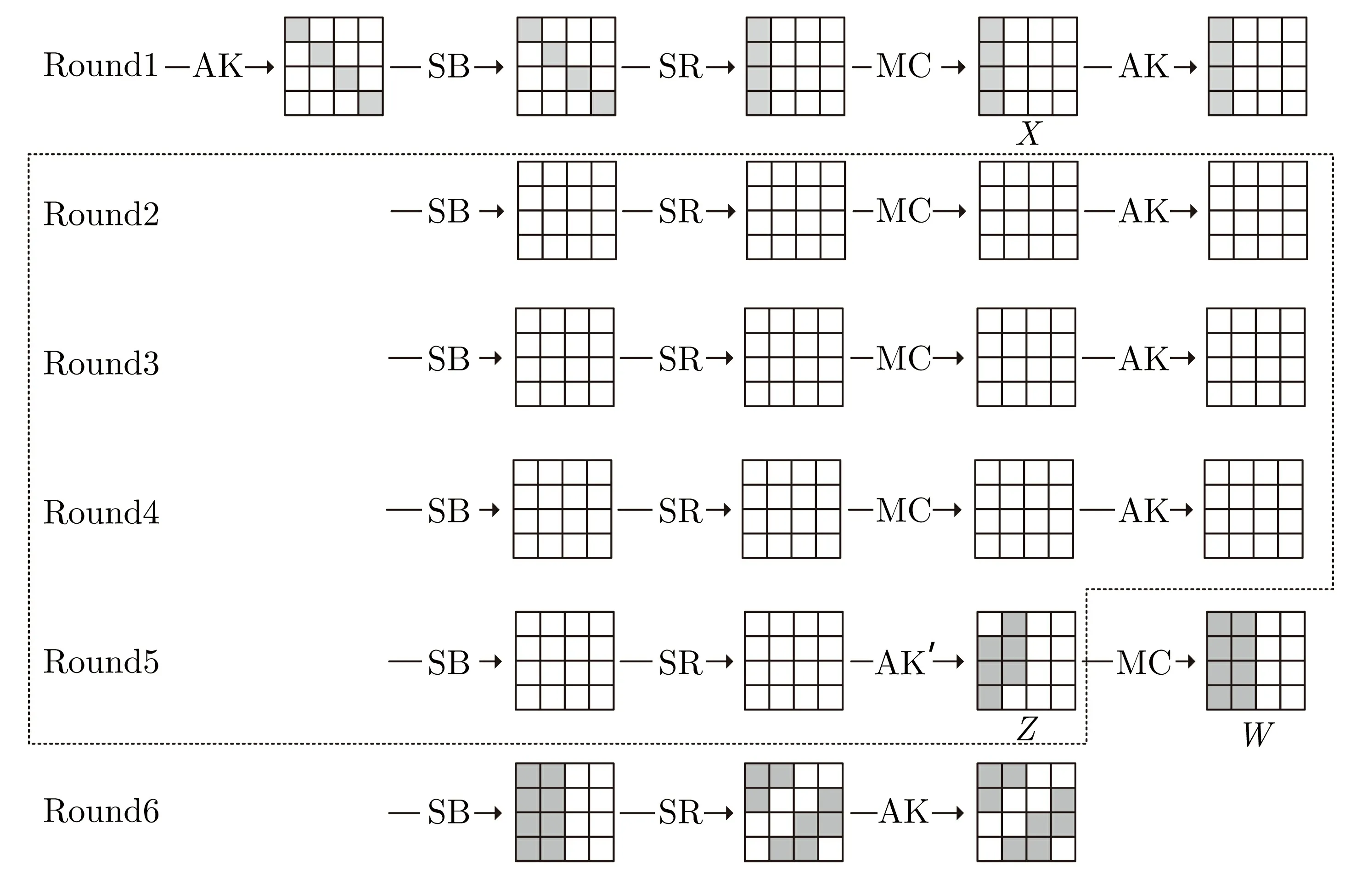
图2 6 轮AES 算法Figure 2 6 rounds of AES

对L中每个明文对和K0，SR-1(col(0))的每次猜测， 构造表L1，i和L2，i的复杂度为2×216×6×2≈220.58次S 盒计算， 表匹配找碰撞的复杂度为2×216×4 = 219次查表， 相当于219次一轮加密， 验证碰撞确定的K6，SR(col(0))的计算复杂度为210×10×4≈215.32次S 盒计算. 所以使用中间相遇技术改进后步骤(2)(a) 的总复杂度为(214×232×(220.58/20+219+215.32/20))/6≈262.62次6 轮AES 加密. 步骤(2)(b) 的计算复杂度为(214×4×232×16×4)/(20×6)≈247.09， 步骤(3) 和步骤(4) 的计算量相比之下可以忽略. 改进的6 轮AES 混合差分攻击算法1 的数据复杂度为215×232= 247， 时间复杂度为262.62.筛选满足密文差分条件的明文对时构建Hash 表的大小为232， 表L1，i和L2，i的大小均为216， 表T的大小约为28， 所以算法的主要存储复杂度为明密文数据存储. 算法成功的概率等于L中214个明文对存在Good Pair 的概率1-(1-2-14)214≈1-e-1≈63%. 如果将密文筛选条件(C1+C2)SR(col(2，3))=0 改为任意两条反对角线差分为0， 算法1 仍然有效. 我们仍在214个对中寻找Good Pair， 数据和存储复杂度可降为247/6≈244.42， 时间复杂度和成功率不变.

算法1 AES 的6 轮混合差分攻击选择215 个明文结构， 每个明文结构第0 条对角线遍历、其余字节取随机固定值. 询问加密机获取它们的密文.对每个明文结构， 以密文的第2、3 条反对角线的值构建Hash 表， 将满足密文差分(C1 +C2)SR(col(2，3)) = 0 的明文对(P1，P2) 存入表L 中.for L 中每个明文对(P1，P2) do for 猜测K0，SR-1(col(0)) do部分加密1 轮到(X1，X2)， 由X1，col(0) 和X2，col(0) 构造7 个混合结构(Xj3，Xj4)， 1 ≤j ≤7.对Xj3，Xj4 部分解密1 轮得到其明文Pj3，Pj4， 查询获得相应的密文Cj3，Cj4， 1 ≤j ≤7.for 猜测K6，{0，13} do分别对(C1，C2)， (C13，C14)， (C23，C24) 部分解密计算ΔZi 关于ΔW{0，1} 的部分和， 并将它们级联以K6，{0，13} 为索引存入表L1，i 中， i = 0，1，2，3;end for 猜测K6，{7，10} do分别对(C1，C2)， (C13，C14)， (C23，C24) 部分解密计算ΔZi 关于ΔW{2，3} 的部分和， 并将它们级联以K6，{7，10} 为索引存入表L2，i 中， i = 0，1，2，3;end for 0 ≤i ≤3 do对表L1，i 和L2，i 进行匹配找碰撞， 将碰撞对应的索引K6，{0，7，10，13} 存储到表T 中;for T 中K6，SR(col(0)) 的每个候选值do部分解密(Cj3，Cj4)， 如果存在(Zj3 +Zj4)i /= 0， 3 ≤j ≤7， 则将该候选值从表T 中删除;end if T 不是空集then利用(Z1 +Z2)SR(col(i)) = (Zj3 +Zj4)SR(col(i)) = 0， 1 ≤j ≤7 分别筛选K6 的另外三条反对角线.end end end end对候选的K6 进行加密验证.

4 PRINCE 和PRINCEcore 的6 轮混合差分攻击

4.1 PRINCE 算法简介

PRINCE 算法的分组长度为64 比特， 密钥长度为128 比特， 迭代轮数为12 轮， 算法结构如图3 所示.64 比特状态用4×4 的矩阵来描述时， 矩阵中每个元素是一个4 比特块. 128 比特的密钥被分为2 个64比特的子密钥k0和k1， 其中k1应用于算法的核心部件PRINCEcore，k0和k′0用于算法输入、输出两端的白化， 这里k′0=(k0≫1)+(k0≫63). PRINCEcore采用对称结构， 中间2 轮是对合的， 前后5 轮除轮常数不同外互为逆变换. 轮常数满足RCi+RC11-i=α， 0≤i ≤11， 这里α是固定常数. PRINCE算法的解密可以通过加密操作来实现， 即D(k0‖k′0‖k1)(·) =E(k′0‖k0‖k1+α)(·). 本文使用Rn表示n轮的PRINCE 变换， 轮变换包括以下5 个操作:

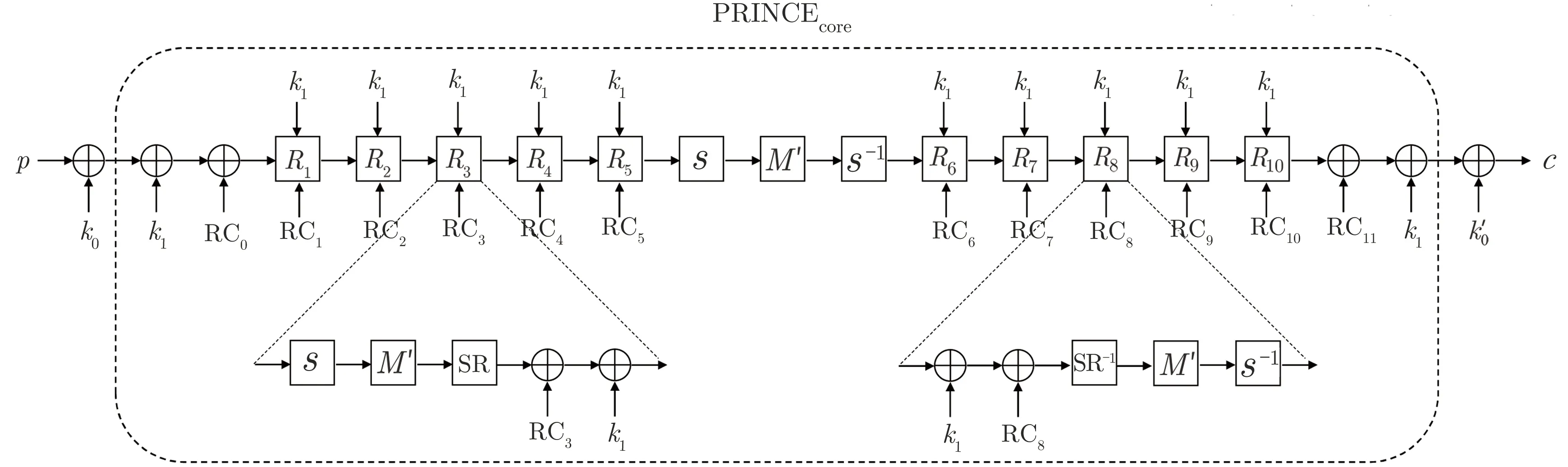
图3 PRINCE 算法Figure 3 PRINCE cipher

-S层: 状态矩阵的16 个块同时查询一个4 比特的S 盒.

- 扩散层(M′): 使用F2上的一个64×64 的矩阵乘以64 比特状态，M′-1=M′.

- 行移位(SR): 将状态矩阵的第i行循环左移i个块， 其中i=0，1，2，3.

- 轮常数加(ARC): 将状态与一个64 比特轮常数RCi异或， 0≤i ≤11.

- 密钥加(AK): 将状态比特异或64 比特密钥k1.

4.2 6 轮PRINCE 的混合差分攻击

由于PRINCE 与AES 具有相似的结构， 所以我们能够得到如下4 轮PRINCE 的混合差分性质.

定理2 设(X1，X2，X3，X4)是PRINCE 的一个混合四元组，则(R4°SR(X1)+R4°SR(X2))col(i)=0当且仅当(R4°SR(X3)+R4°SR(X4))col(i)=0，i ∈{0，1，2，3}.

证明: 忽略不影响差分的AK 和ARC，

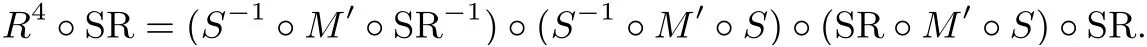
交换SR 与S的顺序，

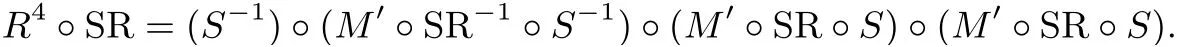
与4 轮AES 相比最后少一个SR. 4 轮混合差分性质与S 盒和列混合矩阵的细节无关， 故结论成立.

图4 6 轮PRINCE 算法Figure 4 6 rounds of PRINCE

4.3 6 轮PRINCEcore 的混合差分攻击

6 轮PRINCEcore如图5 所示. 对6 轮PRINCEcore的混合差分攻击与PRINCE 相似， 选取的明文结构和混合差分区分器均相同. 不同之处在于PRINCEcore没有白化密钥， 轮密钥都是k1， 我们只猜测k1的某一列即可进行明文的部分加密和密文的部分解密， 故计算复杂度与PRINCE 相比有较大减少. 下面介绍6 轮PRINCEcore的混合差分攻击流程.

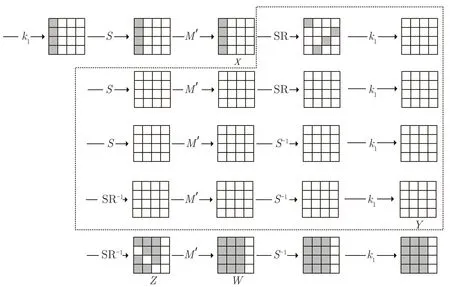
图5 6 轮PRINCEcore 算法Figure 5 6 rounds of PRINCEcore

算法2 PRINCEcore 的6 轮混合差分攻击选择一个明文结构， 在第0 列取所有可能值， 其他字节取任意固定值. 询问加密机获取它们的密文.将216 个密文按照第3 列的值构建Hash 表， 构造满足(C1 +C2)col(3) = 0 的明文对(P1，P2)， 任选其中210个对存储到表格L 中.for L 中每个明文对(P1，P2) do for 猜测k1，{0，1} do对(C1，C2) 部分解密计算ΔZi 关于ΔW{0，1} 的部分和， 以k1，{0，1} 为索引存入表L1，i 中，i = 0，1，2，3;end for 猜测k1，{2，3} do对(C1，C2) 部分解密计算ΔZi 关于ΔW{2，3} 的部分和， 以k1，{2，3} 为索引存储到L2，i 中，i = 0，1，2，3;end for 0 ≤i ≤3 do对表L1，i 和L2，i 进行匹配找碰撞， 将碰撞对应的索引k1，col(0) 存储到表T 中;for T 中k1，col(0) 的每个候选值do对(P1，P2) 进行一轮部分加密得到(X1，col(0)，X2，col(0));for 1 ≤j ≤7 do由X1，col(0) 和X2，col(0) 构造(Xj3，Xj4);对(Xj3， Xj4) 部分解密一轮得到明文(Pj3，Pj4)， 查询获得密文(Cj3，Cj4);部分解密(Cj3，Cj4)， 如果ΔZi /= 0， 将该候选值从T 中删除;end end if T 不是空集then利用(Z1 +Z2)SR-1(col(-i mod 4)) = (Zj3 +Zj4)SR-1(col(-i mod 4)) = 0， 1 ≤j ≤7 分别筛选K0 的另外三列.end end end对候选的k1 进行加密验证.

5 结论

文献[14] 和[15] 表明混合差分攻击可以将数据和存储复杂度限制到较小的程度， 而不追求时间复杂度的最优. 本文在文献[14，15] 中的6 轮AES-128 混合差分攻击的基础上， 通过对密文差分增设条件限制来提高Good Pair 出现的概率， 减少了每次密钥猜测需要验证的数据对数， 将6 轮AES-128 混合差分攻击的时间复杂度由273改进到262.62， 数据和存储复杂度提高到244.42. 在所有6 轮AES-128 的密钥恢复攻击中， 本文攻击方案的总复杂度优于除了积分攻击以外的其他所有攻击. 将改进的6 轮混合差分攻击应用于PRINCE 和PRINCEcore， 我们给出了总复杂度分别为230.66和222的密钥恢复攻击， 其中6轮PRINCEcore的攻击结果优于积分攻击和差分攻击. 如何以追求时间复杂度、总复杂度最优为目标改进AES 和PRINCE 的混合差分攻击是值得后续深入研究的问题.