基于通用计算平台SM4-CTR 算法并行实现与优化*

李晓东， 胡一鸣， 池亚平， 钱 榕， 张健毅

北京电子科技学院， 北京 100070

1 概述

随着大数据、云计算、5G 等新技术的快速发展和广泛应用， 在高速网络系统中如何保证数据传输的安全可靠高效成为目前研究的热点之一. 密码算法一直是确保国家和经济生产活动中数据传输安全的关键， 尤其是国产密码算法的研究日益重要. SM4 算法[1]是目前国产密码算法中广泛应用于金融、工业生产等领域的重要算法之一.

GPU 的概念是由NVIDIA 公司于1999 年提出的， 它是显卡上的一块芯片， 外接在PCI-E 接口， 主要用作辅助处理. GPU 自诞生起面对的就是类型高度统一的、相互无依赖的大规模数据和不需要被打断的纯净的计算环境. 在2007 年CUDA 发布后， GPU 编程不需要再借用图形API， 开发者只需要通过C语言就可以进行编程， 从而大大降低了开发的门槛. 此后， GPU 不再只能处理图像， 同时还可以通过调整线程块大小、存储空间使用、数据传输模式等手段对计算密集型和易于并行的程序进行优化， 使其运行速度更快、效率更高[2].

分组密码的工作模式可以对原有的分组密码算法进行加强， 使分组密码能够应用于实际加密中， 且不同的工作模式其性能和安全性也完全不同， 合适的工作模式可以弥补分组密码算法的缺陷. 1980 年，美国国家标准局(现在的NIST) 公布了DES 的4 种工作模式: ECB (电子密码本， electronic code book)、CBC (密文分组链接， cipher block chaining)、CFB (密文反馈， cipher feedback)、OFB (输出反馈， output feedback)， 之后在2001 年， 新增了由Diffie 和Hellman 在1979 年提出的CTR (计数器，counter) 模式[3]. 现有的关于分组密码算法工作模式的研究便是在这五种基础工作模式上进行改进. 在CUDA 发布之初的2007 年， Manavski[4]就首次实现了利用CUDA 并行加速AES 密码算法， 并比较了不同的GPU 内存使用对AES 算法计算速度的影响， 为后续其他团队的研究提供了借鉴. 之后， Harrison等人[5]实现了基于CUDA 的AES 算法CTR 模式运行; Nishikawa 等人[6]更是将ECB 模式下的AES密码算法提升到了605.9 Gbps. Kim 等人[7]实现RSA 算法的GPU 加速且加速比可达10 以上. 费雄伟等人[8]研究了明文大小、线程分块、存储选择对CTR 模式的AES 算法并行运算速度的影响， 所得到的综合加速比高达31.59. 可以说， 现在针对对称密码算法和非对称密码算法的CUDA 并行实现和加速已经有了较多的研究.

在CUDA 实现SM4 密码算法并行方面， 杨海云等人[9]基于CUDA 分别实现了AES 和SM4 算法并行; 王德民等人[10]从明文大小角度研究CUDA 并行对SM4 算法运行速度的影响， 当明文过小时，CPU 和GPU 之间的数据传输耗时较长， 无法起到很好的加速作用， 当明文较大时， 加速比显著增加后会趋于平稳， 不会无限制的扩大; 张才贤[11]针对SM4 认证加密方面设计出一套新的GCM 工作模式用于高速认证中的加密模块; Cheng 等人[12]基于GPU 设计了一种高性能并行对称密码服务器， 通过GPU内存选择和优化CPU 和GPU 之间的数据传输， 数据加密速度可达到15.96 Gbps， 是现有对称加密服务器速度的23 倍. 其他的研究工作包括SM4 的专用硬件实现[13]、多模式实现[14]以及针对SM4 实现的攻击[15-17].

综上所述， 目前针对SM4 算法的研究大多是采用传统的ECB 模式在CPU 或GPU 上进行实现和优化. 而除去传统的ECB 工作模式， 多数团队针对SM4 算法的研究集中于在特定使用场景设计新的工作模式或利用软件实现算法的快速运行. 由此可见， 已有的研究存在如下问题:

(1) 采用传统工作模式在安全性方面有所欠缺;

(2) 实验平台通用性不够;

(3) 算法优化后针对运行效果讨论不足.

本文在全面分析GPU 下并行计算的特点的基础上， 在通用计算机平台上对国密分组密码SM4 算法的CTR 模式在GPU 上并行实现策略进行了深入讨论， 本文具体贡献有:

(1) 系统地分析核函数设计、明文大小、线程块大小等对算法的影响. 在设计出SM4-CTR 算法的核函数后， 对线程网格、线程块大小以及内存类型选择进行优化， 实现了并行加解密;

(2) 实现了SM4-CTR 在不同架构GPU 下的并行化算法， 并对比了不同架构GPU 的加速效果及CTR 相对于传统工作模式的加速效果. 选择不同架构的新旧两个GPU 实验环境， 分别研究优化后的SM4-CTR 运行效果， 并与相同条件下利用CPU 串行运行和基于传统工作模式并行运行的结果进行对比. 实验发现， GPU 平台面对较大明文时， 相比于计算能力有限的CPU 具有较大的性能优势; CTR 模式在安全性能提高的同时， 其并行运行的速率也优于传统工作模式;

(3) 系统性地对比了SM4-CTR 的CPU、GPU 以及快速软件优化的运行效率， 为SM4 算法的应用以及未来相关的研究奠定基础. 利用实验结果与之前团队的研究成果进行对比， 结果显示本文提出的方案在通用计算机平台的运行效果大幅优于传统工作模式下利用CPU、GPU 和快速软件优化的运行效果.

2 SM4 的工作模式

2.1 SM4 密码算法

SM4 是2006 年中国国家密码管理局发布的用于商用领域的分组密码算法， 在2016 年成为国家标准.SM4 密码算法为非平衡Feistel 结构分组密码算法， 分组长度和密钥长度都为128 位， 加解密过程和密钥扩展都采用32 轮非线性迭代结构， 加密算法和解密算法结构相同， 只有轮密钥的使用顺序相反. SM4 密码算法由密钥扩展算法和加解密算法组成， 加解密算法中最为重要的就是轮函数F.

SM4 密码算法的密钥长度为128 位， 表示为: MK = (MK0，MK1，MK2，MK3)， 其中MKi(i=0，1，2，3) 为32 位. 轮密钥表示为: rk0，rk1，···，rk31， 其中rki(i=0，1，···，31) 由128 位MK 经32 轮迭代生成.

轮密钥rki计算公式如下:

轮函数F是SM4 算法加解密过程的重要组成部分， 它主要由非线性变换τ和线性变换L组成， 先将128 位的明文x分成4 个32 位的Xi(i= 0，1，2，3)， 再经32 轮迭代， 公式(其中i= 0，1，···，31) 如下:

经过32 轮迭代后， 明文x新生成了32 个位Xi， 记为:Xi(i= 0，1，···，35)， 则密文y表示为:y=(Y0，Y1，Y2，Y3)=(X35，X34，X33，X32). 轮函数F和完整SM4 算法加密流程如图1 所示.

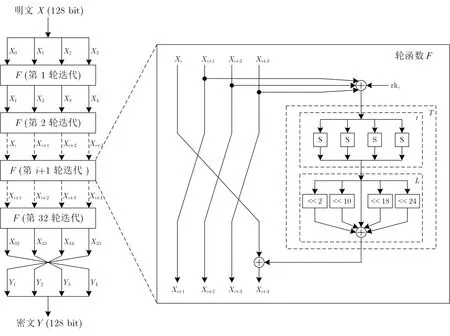
图1 轮函数F 计算流程和SM4 加密流程Figure 1 Round function F calculation process and SM4 encryption process

SM4 算法的解密过程与加密过程基本一致， 只是轮密钥使用顺序不同. 加密轮密钥使用顺序为rk0，rk1，···，rk31， 解密轮密钥是加密轮密钥的逆序， 即rk31，rk30，···，rk0.

2.2 ECB 模式

ECB 模式是最简单直接的也是最传统常用的工作模式， 直接将明文分成固定大小的块， 每个块独立地进行加密， 在加密时需要将明文填充至块大小的整数倍. ECB 模式下加解密公式为:

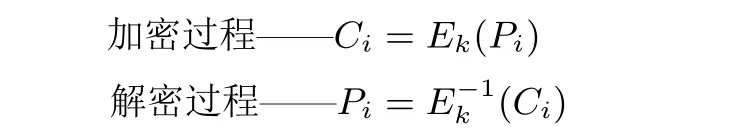
其中，C代表密文，P代表明文，Ek代表加密，代表解密.

ECB 工作模式优点有:

(1) 简单， 计算速度快;

(2) 支持并行计算;

(3) 运算错误不会被传送， 无需知道明文长度.

ECB 工作模式缺点是:

(1) 加密长度必须是分组长度的整数倍;

(2) 加密过程是高度确定的， 只要密钥不发生改变， 同样的明文加密后密文也相同， 易受到攻击;

(3) 无法检测密文分组的顺序， 无法抵抗分组的重放、嵌入、删除攻击.

这些缺点导致ECB 模式非常不安全， 实用性不强， 现在ECB 模式仅用于一些较短明文的加解密.ECB 模式加解密流程如图2 所示.

图2 ECB 模式加解密Figure 2 ECB mode encryption and decryption

2.3 CTR 模式

CTR 模式， 是一种类似于流密码的模式， 加密算法只是用来产生密钥流与明文分组异或. 该模式加密的输入是一个计数器值， 加密后再与明文数据进行异或得到密文， 其中计数器的值应该是互不相同的.

CTR 模式下的加解密公式如下:

其中， ctr 代表计数器值，C代表密文，P代表明文，Ek代表加密.

CTR 工作模式优点有:

(1) CTR 模式的加密和解密使用了完全相同的结构， 因此在程序实现上比较容易;

(2) CTR 模式中能够以任意顺序处理分组， 这就意味着能够实现并行计算， 在执行并行计算的系统中CTR 模式的速度是非常快的;

(3) CTR 模式中加解密相同， 安全性好.

CTR 工作模式缺点有: 需要加解密双方要保持同步.

CTR 模式加解密流程如图3 所示.

图3 CTR 模式加解密Figure 3 CTR mode encryption and decryption

3 基于CTR 的GPU 并行SM4 算法

3.1 并行化策略

CTR 模式与传统SM4 算法采用的ECB 模式相似， 加解密过程都支持并行， 但CTR 模式中引入了计数器值， 而计数器值本身也会占用一定量的GPU 全局内存空间， 所以在设计核函数时需要针对这一点进行相关的改进. 并行方式如图4 所示.

图4 CTR 模式加解密并行Figure 4 CTR mode encryption and decryption parallel

其中，P是128 位明文块，C是128 位密文块， rk 是加密轮密钥，E是加密过程，n是线程总数. 加密过程和解密过程完全一样， 只有输入不同， 加密时输入明文输出密文， 解密时输入密文输出明文. 每个线程独立完成自己的计算， 各线程之间互不干扰.

3.2 并行化实现

主机端负责CTR 模式下的SM4 算法的初始化和接收阶段， 设备端负责加解密计算， 并行化实现主要包括主机端初始化阶段、设备端并行计算阶段、主机端结束阶段这三个阶段.

3.2.1 主机端初始化阶段

这一阶段的任务主要是将密码算法所用到的密钥、明文、密文等数据传输到GPU 内存中.

(1) 利用fopen() 函数读取明文数据text， 并生成密钥key;

(2) 生成S 盒数据存于GPU 内存中;

(3) 生成一个随机的计数器值counter;

(4) 根据密钥key 生成加密轮密钥rk 和解密轮密drk:SM4Key(key， rk， 0);SM4Key(key， drk， 1);

(5) 设置运行GPU， 单GPU 系统不需要这一步， 多GPU 系统默认使用第0 号GPU (在之后的内容中不再提及此步骤):cudaSetDevice(0);

(6) 为明文p、密文c、轮密钥rk、计数器值counter 申请GPU 全局内存空间:cudaMalloc((void**)&p，size*sizeof(muint8)); //明文cudaMalloc((void**)&c，size*sizeof(muint8)); //密文cudaMalloc((void**)&rk，32*sizeof(muint32)); //轮密钥cudaMalloc((void**)&counter， 16*sizeof(muint8)); //计数器值其中， size 代表明文的字节数;

(7) 向GPU 发送明文数据text、轮密钥数据rk、计数器值counter:cudaMemcpy(p， text， size*sizeof(muint8)， cudaMemcpyHostToDevice); //明文cudaMemcpy(rk， key， 32*sizeof(muint32)， cudaMemcpyHostToDevice); //轮密钥cudaMemcpy(counter， Counter， 16*sizeof(muint8)， cudaMemcpyHostToDevice); //轮密钥

(8) 向GPU 发送明文数据text、轮密钥数据rk、计数器值counter:SM4_encrypt_ctr≪＜blocks，threads≫＞(p，c，rk，n，counter).

3.2.2 设备端并行计算阶段

这一阶段通过线程划分、启动进行加解密计算.

(1) 确认线程id: inti=(blockIdx.x*blockDim.x)+threadIdx.x;

(2) CTR 模式中算法输入为计数器值， 每个计数器值都不相同:

(3) 启动线程， 并将线程所需要进行计算的数据存于该线程独占的寄存器中:SM4_ctr_encrypt_thread(ca，&(c[i*16])，rk，&(p[i*16]));

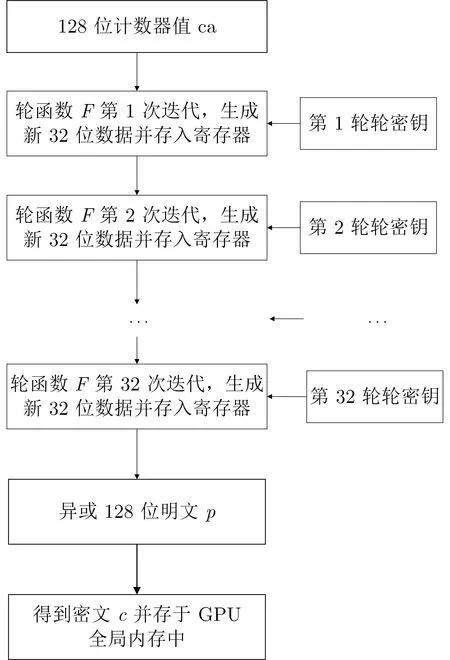
图5 CTR 模式SM4 线程内算法Figure 5 SM4 in-thread algorithm in CTR mode

(4) 核函数计算完成后， 之前为密文c申请的GPU 全局内存已经存储了计算完成后的密文.

3.2.3 主机端结束阶段

这一阶段主要将数据传输回主机端， 并释放内存.

(1) 将GPU 全局内存中的密文数据传回CPU:cudaMemcpy(cipher，c，size*sizeof(muint8)，cudaMemcpyDeviceToHost);

(2) 释放GPU 上明文、密文、轮密钥数据:

4 实验及其分析

4.1 CUDA 编程对性能影响

GPU 上实现密码算法的并行计算， 需要考量的方面非常多， 这些方面的合理与否， 直接影响着密码算法的执行速度. 它包括:

(1) 线程束分配线程束作为CUDA 最小的执行单位， 要确保束内有32 个线程， 线程块内有32 的整数倍个线程，线程束在进行数据传输时也要考虑到内存地址的影响， 避免出现全局内存非合并的情况发生.

(2) 内存选择和使用不同内存的大小、延迟、使用方法各不相同， 在使用的时候应该考虑到各内存的特点. 比如对于S 盒这类小体量的数据存放在常量内存或共享内存就比存放在全局内存可得到更优的密码算法运算速度. 同时， 在使用共享内存的时候， 要尽量避免bank 冲突(bank-conflict)， 这会让原本并行的对共享内存的访存操作变成串行从而极大地降低程序效率.

(3) 线程块大小一个线程块内要有足够多的线程， 因为一个线程块会占用一个SM，如果块内线程过少会导致SM内多个Core 闲置.

(4) 线程数目线程数目的大小直接决定并行规模， 是最主要影响算法并行计算速度的因素， 应尽可能的增加线程数量.

CUDA 最大的特点就是其高度的编程自由性， 开发人员可以根据自己的需求对程序进行修改， 但也因为其自由性导致在CUDA 代码编写的时候要考虑多方因素， 任何一个微小的差别都可能对程序的执行速度造成巨大的影响.

4.2 实验环境

为了研究SM4 算法CTR 模式下GPU 并行的效果， 首先要读取出实验计算机中的相关参数， 在这里可以通过编写CheckGPU 程序， 确定自己电脑GPU 各项数据和实验环境， 其中要用到cudaGetDevice-Count、cudaGetDeviceProperties 等函数. 为了全面分析本文设计实现的SM4-CTR 算法的并行方案的可行性和高效性， 本文搭建了两个不同测试实验环境(如表1 所示) ， 并在这两个实验环境中进行了多角度实验数据的采集和分析. 总的来看， 虽然两个实验环境的计算性能有很大差异， 不同平台所得到的加速比也不同， 但是加速比的变化趋势是一样的. 其中实验环境1 为目前新的显卡架构， 属于通用计算平台.

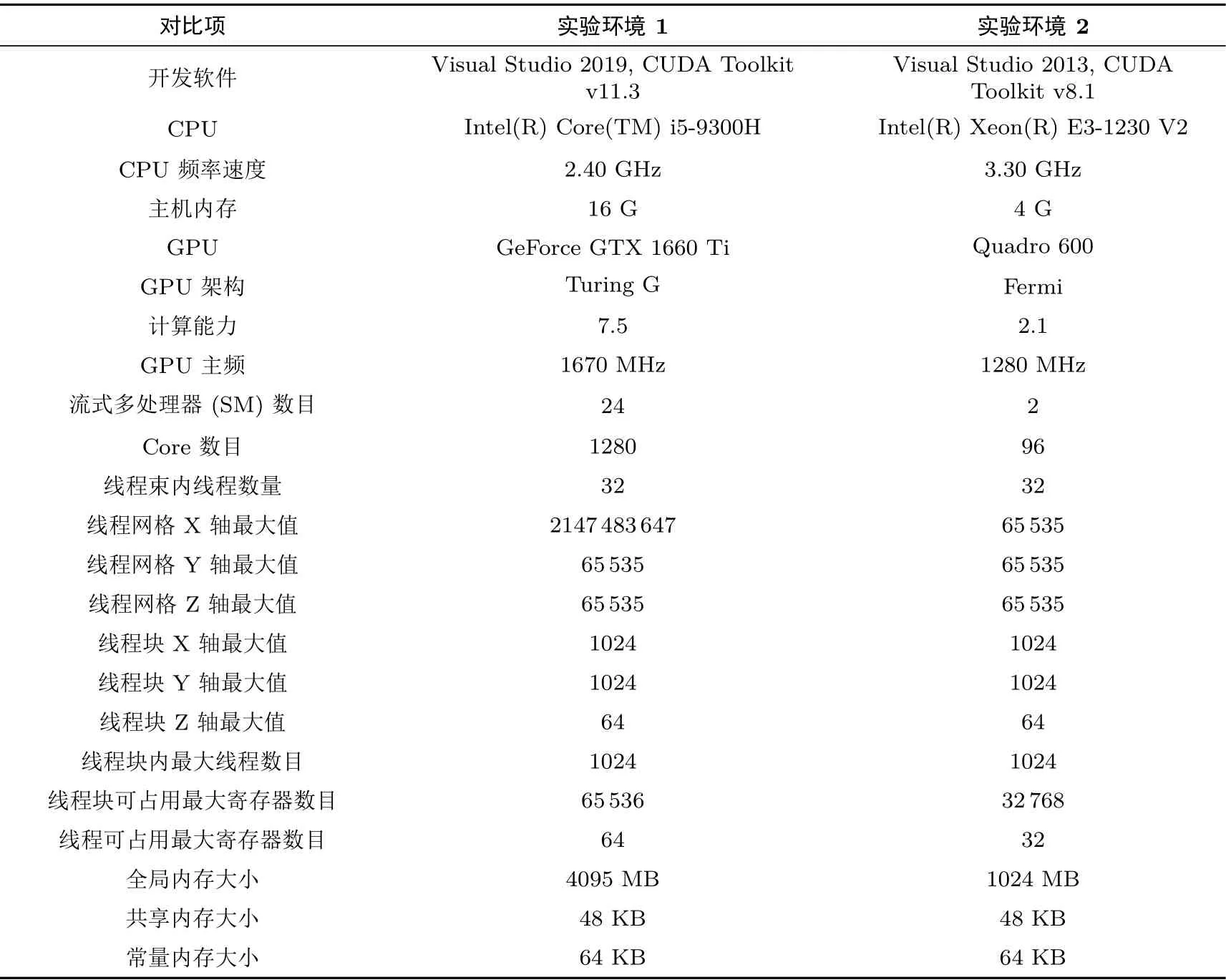
表1 实验环境Table 1 Experiment environment

4.3 CTR 模式性能分析实验结果

实验主要通过CTR 模式下串行加解密和并行加解密时间的比值来衡量GPU 并行加速的效果， 其公式如下:

其中，TC代表CPU 串行执行加解密所需要的时间，TG代表GPU 并行执行加解密所需要的时间，Tt代表在GPU 上分配内存、释放内存以及CPU 与GPU 之间的数据传输所需要的时间，Tg代表GPU 并行进行计算所需要的时间，Tt+Tg表示GPU 并行执行加解密所需要的时间TG.

4.3.1 不同明文大小

在实验环境1 中， SM4 算法的CTR 模式下同时利用CPU 串行和GPU 并行加解密一次不同大小的明文， 其中明文大小选取从16 KB 到256 MB， 每个线程块中都是1024 个线程， 根据最后的结果计算加速比， 结果如图6 所示.

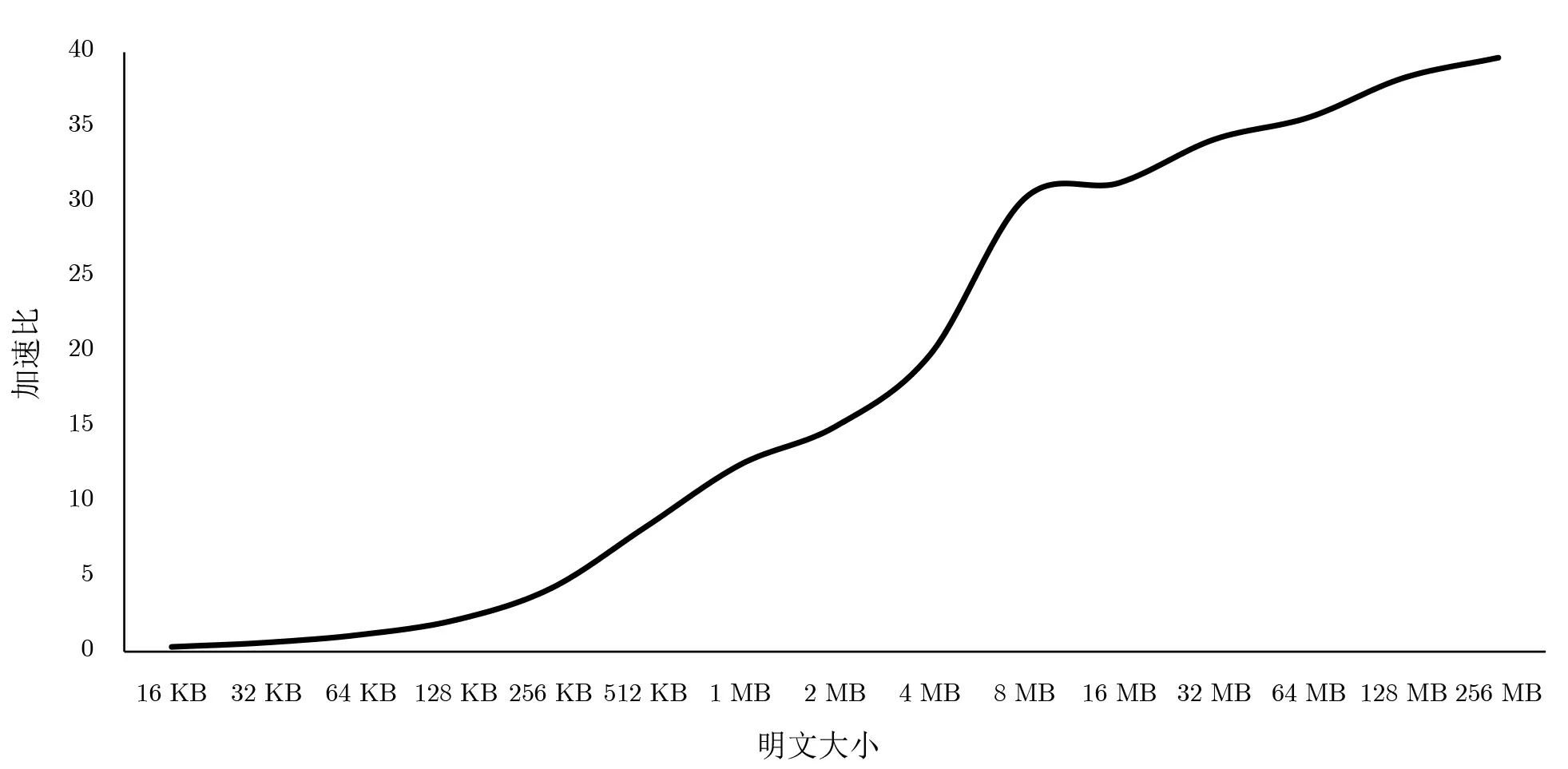
图6 不同明文大小的并行加速比Figure 6 Parallel speedup of different plaintext sizes

从实验结果中可以看出来， 当明文数据小于64 KB 左右的时候， 利用GPU 对SM4 算法进行并行执行， 算法运行速度还不如串行执行， 但在之后加速比逐渐提高， 并且随着明文的加大加速比也在提高， 最终加速比大致能达到40 倍. 同时在明文数据等于16 KB、32 KB、64 KB 的时候， GPU 并行计算时间TG几乎相同， 这是因为线程块的数目分别为1 个、2 个、4 个， 而实验环境中GPU 的SM (流式多处理器)有24 个， 也就是说最大允许24 个线程块同时参与计算， 当明文数据较小时， 有部分SM 处于闲置状态，这时提升线程块的数目并不会拖慢GPU 计算速度.

可知虽然并行执行SM4 算法可以提升算法执行速度， 但不能无限制地增大， 一方面由于GPU 虽然可以实现上千个线程同时执行但Core 数量也是有限的， 当线程过多的时候， 多余的线程只能等待其他线程执行完毕， 另一方面GPU 上SM4 算法的计算速度已经快过数据传输速度， 算法并行性不再是限制算法执行速度的瓶颈， 反而是总线传输数据的速度限制了算法的执行速度.

4.3.2 不同线程块大小

在实验环境2 中， 选取8 MB 大小的明文， 令SM4 算法的CTR 模式进行并行加解密计算， 期间仅改变线程块大小， 同时为了防止单次加解密的误差， 这里进行100 次计算， 实验结果如表2 所示.

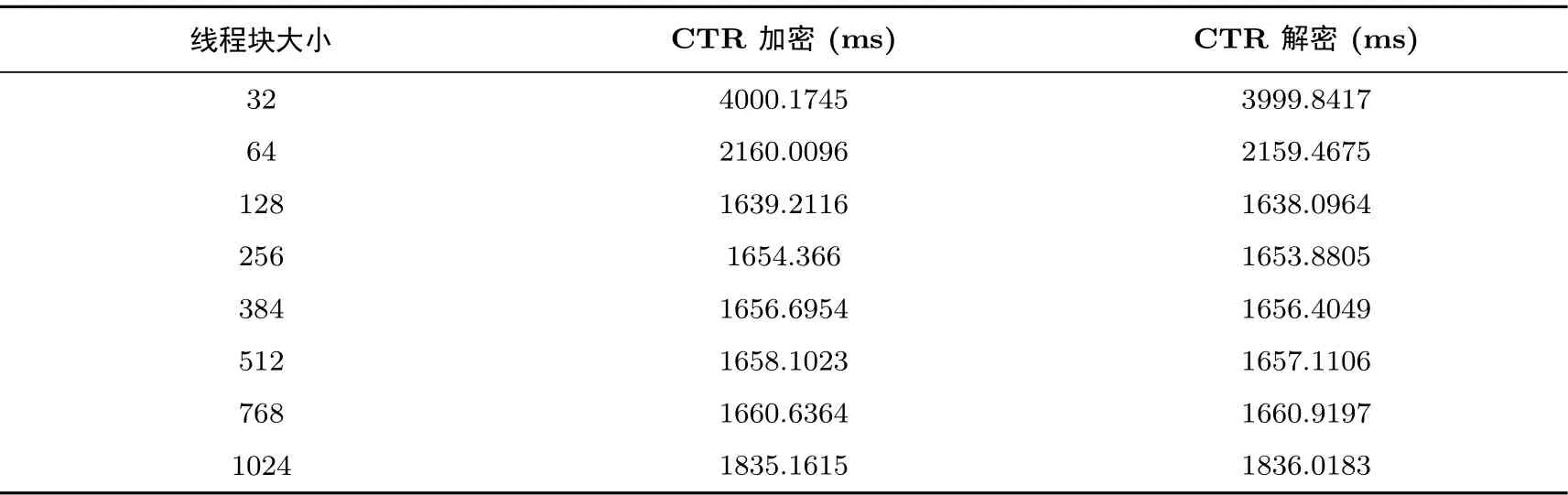
表2 不同线程块大小CTR 模式并行加解密速度Table 2 Parallel encryption and decryption speed in CTR mode with different thread block sizes

根据实验结果， CTR 模式当线程块大小较小的时候， 即使线程数目没有改变， 也会影响算法的计算速度， 这是由于一个线程块在进行计算时就会占用一个SM， 无论线程块的大小都肯定占用一个， 所以当线程块过小的时候SM 中会有大量的Core 不参与计算从而浪费了GPU 资源; 当线程块的大小在128～768 之间时， SM4 算法的计算速度大体相同， 大约在256 时达到最高的运算速度; 当线程块接近1024 时， 计算速度又有所减慢， 这是由于虽然一个SM 可以最大承载1024 线程同时参与运算， 但在数据调用的时候还是会出现一定的冲突， 比如调用密钥的时候， 导致计算速度有少许的减慢.

基于上述结论， 当线程块的大小在1～128 之间时， 随着线程块的增大， SM4 算法的计算速度应该是不断增加的; 当线程块大小在128～768 之间时， SM4 算法的计算速度应该不会有太大的改变. 但表3 并不符合这一规定.

表3 线程块划分对CTR 模式加解密速度的影响Table 3 Influence of thread block division on speed of CTR mode encryption and decryption

前文提到， CUDA 中同一个线程块的线程会自动以32 为单位组成线程束， 这是CUDA 最小的调度单位， 也就是说同一个束的线程要同时参与计算. 但是CUDA 的高自由性又允许程序员将线程块的大小规定成1～1024 之间的任意整数， 出现线程块的大小不为32 的整数倍的情况， 这就会造成最后一个线程束不满32 个线程， 但它还是会占用一个完整线程束的运算单元， 造成GPU 资源浪费. 这就导致线程块在64 和512 时SM4 算法计算速度明显要大于70 和520， 这一规则也适用于其他线程块不为32 的整数的情况， 所以在规划线程块大小的时候应尽量选择32 的整数倍.

4.4 CTR 模式与ECB 模式对比实验结果

本次实验是在实验环境2 中， 通过公式计算出ECB 和CTR 工作模式下的SM4 算法加解密加速比，对比两种模式之间的差别.

在实验环境2 中， SM4 算法的CTR 模式和ECB 模式下同时利用CPU 串行和GPU 并行加解密一次不同大小的明文， 其中明文大小选取从16 KB 到512 MB， 每个线程块中都是1024 个线程， 根据最后的结果计算加速比， 结果如图7 所示.

从图7 中可以看出， 当明文数据小于64 KB 左右的时候， 利用GPU 对SM4 算法进行并行执行， 算法运行速度还不如串行执行， 但在之后加速比逐渐提高， 在2 MB 左右的时候提升速度最快， 但明文数据再增大的时候， 加速比提升速度逐渐减慢， 最终ECB 模式SM4 算法停在18 左右， CTR 模式SM4 密码算法停在21 左右.

图7 不同明文ECB、CTR 模式加速比Figure 7 Acceleration ratios of different plaintext ECB and CTR modes

由此可以看出， 前文关于CTR 模式在并行执行运行的情况下速度会更快的推断是正确的， 在明文越来越大的情况下CTR 模式加解密速度也越来越快， 同时实验2 的环境下GPU 架构并不是最新的， 因此在目前现实环境中新的架构下CTR 模式并行运行的加解密速度会比ECB 模式快更多. 而基于前文分析，CTR 模式的安全性天然优于ECB 模式， 因此CTR 模式在实际生活中应用范围会更广， 尤其是有海量数据需要处理的情况下.

5 对其他相关工作对比分析

5.1 SM4 不同运行方式对比

根据上一章在实验环境1 下进行的实验结果计算后发现， 在通用计算平台经过上文方式实现和优化后， CTR 模式下SM4 并行加密或解密速率能达到: 14 194.4 Mbps. 根据这个结果， 与之前开展过的相关实验进行对比， 如表4 所示.

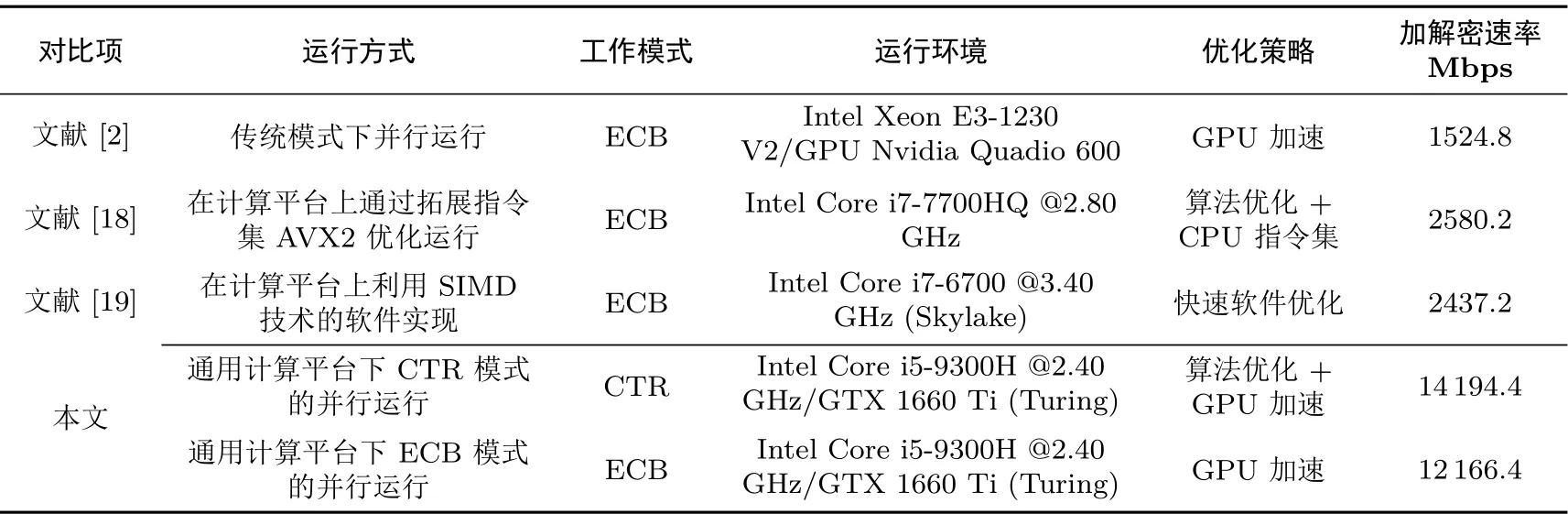
表4 对比结果Table 4 Comparing results

通过上述对比我们可以发现以下几点:

(1) 文献[2] 中， 李秀滢等人采用的是一种在旧的架构环境下通过传统模式将SM4 算法在GPU 上实现并行计算且优化不明显， 因此加解密速率大幅低于本文优化后CTR 模式下在最新GPU 架构的通用计算平台并行运行的结果;

(2) 文献[18] 中， 张笑从等人是基于CPU 上的指令集同时利用比特切片技术对SM4 算法进行优化，其速率显著低于本文利用GPU 模型运行的结果;

(3) 文献[19] 中， 郎欢等人利用SIMD 技术实现SM4 算法的快速软件实现， 虽然其硬件性能和架构优于本文的实验平台， 但速率依然显著低于本文.

为使对比更加精确， 选取8 MB 大小的明文在文献[2] 相同的实验环境进行加解密实验， 得出基于本文提出的CTR 模式优化后的并行加解密速率约为3904 Mbps， 依旧快于文献[2] 中速率.

5.2 对比结果分析

经过上文对比可以发现， 基于本文提出的优化后的SM4-CTR 模式在基于CUDA 模型的最新通用计算平台下加解密速率显著快于传统工作模式下利用CPU 优化、GPU 优化以及利用软件优化的SM4 算法加解密速率. 同时在旧平台， 本文的优化方案依旧快于传统SM4 工作模式的加解密速率.

综上所述， 本文提出的优化后的基于CUDA 模型下SM4-CTR 模式在通用计算平台中可以取得出色的加解密运行速率.

6 结束语

本文针对分组密码算法SM4 基于传统工作模式运行安全性低、利用CPU 串行运行效率低、算法优化多依靠专门硬件平台通用性低的问题， 提出基于通用计算机平台的SM4-CTR 算法在CUDA 编程模型下利用GPU 并行运行的方式提高算法的运行安全性、运算效率和算法应用的范围. 在研究CUDA 编程对加解密算法性能的影响的基础上， 通过本文的优化在最新的通用计算机GPU 架构环境下， 可将SM4 算法的运行速度提高到接近40 倍. 同时研究发现， 不同大小的明文数据块和线程块大小的划分对加解密影响较大， 低于64 KB 的小明文利用GPU 并行无法起到提速的效果， 而线程块划分应当为32 的整倍数， 同时还需要根据明文的特点选择合适的划分， 否则会因为有线程块闲置而导致加解密算法并行运行的效果不理想. 通过多项对比实验， 发现在本文给出的实验环境中CTR 模式在高于256 KB 明文的时候并行运行的加解密的效果优于传统的ECB 模式; 对比之前研究团队在传统工作模式下利用CPU 优化、利用GPU优化和利用软件快速实现优化的运行效果， 本文运算效率均大幅领先.

综上所述， 本文提出的优化后的CTR 模式下SM4 分组算法在通用计算平台下经过GPU 加速后并行运行加解密效率有显著提升， 在安全性、运算速率提高的同时适用平台也更加广泛. 因此， 本文方案在实际生活中针对大数据和个人数据的安全保护中必将发挥巨大的作用. 未来， 我们将密切关注GPU 架构和分组密码算法的工作模式的发展， 本文提出的算法优化方案也会根据实际情况不断优化迭代以适应现实的需求.