一类新的代数免疫度最优的奇变元旋转对称布尔函数的构造*

王 勇， 郑 东，2， 赵庆兰， 李路阳， 师 宇

1. 西安邮电大学 无线网络安全技术国家工程实验室， 西安 710121

2. 卫士通摩石实验室， 北京 100070

1 引言

布尔函数[1]在对称密码系统中有着重要的应用， 可以作为流密码中的滤波函数和组合函数， 也可以作为分组密码中的S 盒， 其密码学性质的优劣在很大程度上影响着密码系统的安全性. 若用于密码系统的布尔函数的非线性度较低， 则流密码系统容易受到快速相关攻击[2]， 而分组密码系统容易受到线性攻击[3].为了抵抗Berlekamp-Massey 攻击[4]和Ronjom-Helleseth 攻击[5]， 布尔函数必须具备较高的代数次数.因此， 用于密码系统的布尔函数需要考虑的密码学指标包括: 非线性度、平衡性、代数次数等. Courtois和Meier[6]提出代数攻击之后， 代数免疫度[7，8]成为衡量布尔函数抵抗代数攻击能力的密码学指标. 文献[8] 指出n元旋转对称布尔函数的代数免疫度上界为「n/2若达到此边界， 则表明该布尔函数具有最优的抵抗代数攻击的能力. 2003 年， 快速代数攻击[9]被提出. 若存在代数次数较低的函数g/= 0， 使得f ·g的代数次数不是很高， 则认为对f进行快速代数攻击是可行的. 快速代数免疫度FAI (fast algebraic immunity)[10]用于衡量一个布尔函数抵抗快速代数攻击的能力.

沈黎鹏和陈克非在文献[19] 给出一种新的方案， 其构造函数的非线性度在变元个数n ≥25 时超过了以往同类的构造， 但是在n ≤23 时作者没有给出确定的非线性度， 且没有考虑快速代数攻击等相关问题.而在实际应用中， 代数攻击的出现要求流密码设计中的布尔函数的输入变元个数n至少为15[20，21]， 但是考虑到快速计算的需求， 特别是在轻量级密码算法的设计中， 变元个数也不宜过大. 文献[22] 指出变元个数n在18 左右即可以满足密码学性质和计算效率的需要. 本文给出一种新的代数免疫度最优的奇变元RSBFs 的方案， 在变元个数n ≤23 时非线性度是同类构造中最高的. 此外， 新函数具有较高的代数次数，在n= 11，13，15 时， 还具有几乎最优的抵抗快速代数攻击的能力， 为布尔函数的实际应用提供了更多选择.

本文其余章节安排如下: 第2 节给出了布尔函数相关基础知识; 第3 节介绍了整数拆分理论， 并且给出了奇变元RSBFs 的具体构造方案; 第4 节证明了本文构造的函数是代数免疫度最优的， 还给出了非线性度、代数次数、抵抗快速代数攻击能力的分析求解过程; 第5 节是总结全文.

2 预备知识

若f是平衡的， 则有Wf(0n)=0 (这里0n代表长为n的全零向量).

对于f ∈Bn，f和仿射函数之间最小汉明距离表示其非线性度， 记为NL(f)， 即:

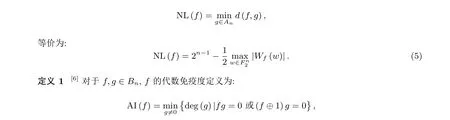
由文献[8] 可知AI(f)≤「n/2若AI(f)=「n/2则f具有最优的抵抗代数攻击的能力.

定义2[10]对于f ∈Bn， 快速代数免疫度用FAI(f) 表示， 即:

其中1≤deg(g)＜AI(f). 若FAI(f) =n， 则称f抵抗快速代数攻击的能力是最优的. 若FAI(f) =n-1， 则称f抵抗快速代数攻击的能力是几乎最优的.

文献[9] 表明， 对于f ∈Bn， 假如存在代数次数较低的函数g以及适当的函数h， 使得f ·g=h， 则说明f不具备良好的抵抗快速代数攻击的能力.f的代数免疫度达到最优， 但并不能说明其具有抵抗快速代数攻击的能力.

定义3[23]如果F(x) 可表示为:

3 构造奇变元旋转对称布尔函数

3.1 整数拆分

首先引入整数拆分[25]的有关理论. 对于一个正整数k和一个长度为m的整数序列， 若满足k1+k2+···+km=k， 其中ki ＞0， 1≤i ≤m， 则称此序列为k的一个m拆分. 该序列是考虑先后顺序的， 也就是说仅仅是不同顺序的序列也代表着k的不同形式的拆分. 例如整数4 的拆分组合为(4)， (3，1)，(2，2)， (2，1，1)， (1，3)， (1，2，1)， (1，1，2)， (1，1，1，1). 由文献[25] 可知， 将一个正整数k拆分为长度为m的分

对于k的m拆分， 若下面(1) 和(2) 两个条件成立， 记为pm(k)， 即:

(1)k1+k2+···+km=k;

(2)km ≥km-1≥···≥k1.

由文献[25] 可知pm(k) 的计数可通过递推公式得到， 即pm(k) =pm-1(k-1)+pm(k-m)， 且满足p1(k)=pk(k)=1.

3.2 构造集合T′h 和T′′h

3.3 构造集合T 和U

3.4 构造函数

其中F(x) 是择多函数. 不难看出， 式(8)中的f(x) 是一个n元旋转对称布尔函数， 且具有平衡性.

例1 当k=5， 即n=11 时， 有:

根据U的构造规则可知:

4 密码学性质分析

4.1 代数免疫度

这里先给出一些证明所需的引理. 引理1 给出了基于择多函数构造代数免疫度最优的布尔函数的方法.

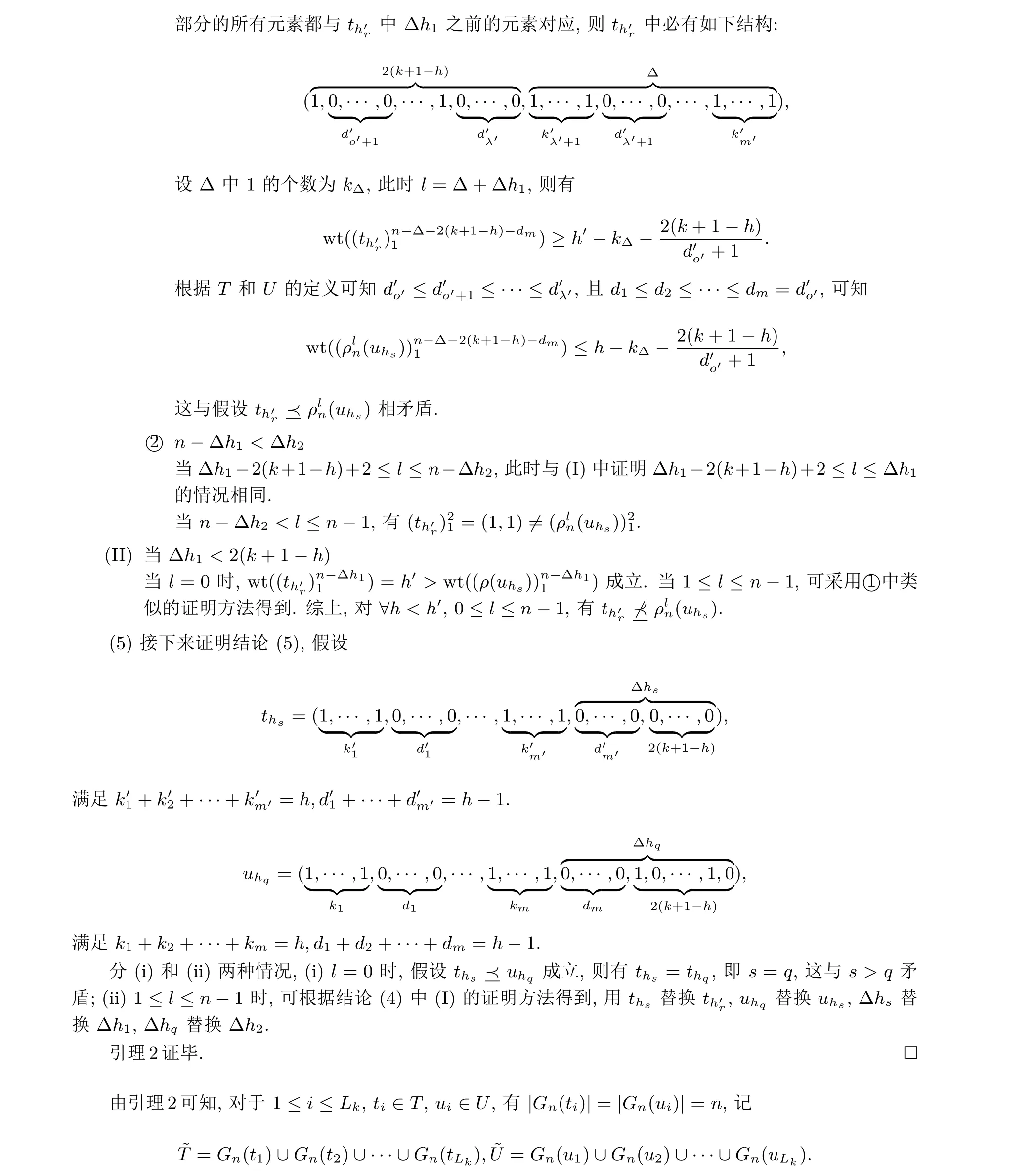
则有|～T|=|～U|=nLk.

定理1 式(8)中的f(x) 具有最优的代数免疫度.

4.2 非线性度

在分析非线性度之前， 先给出一些必要的引理.

表1 将本文构造的布尔函数f(x) 的非线性度相对于择多函数的增加部分与同类研究成果进行了对比， 当变元个数小于25 时本文所构造的函数的非线性度高于现有的所有同类构造， 且增加幅度较为显著，当变元个数大于等于25 时f(x) 的非线性度也高于除文献[19] 之外的同类构造.

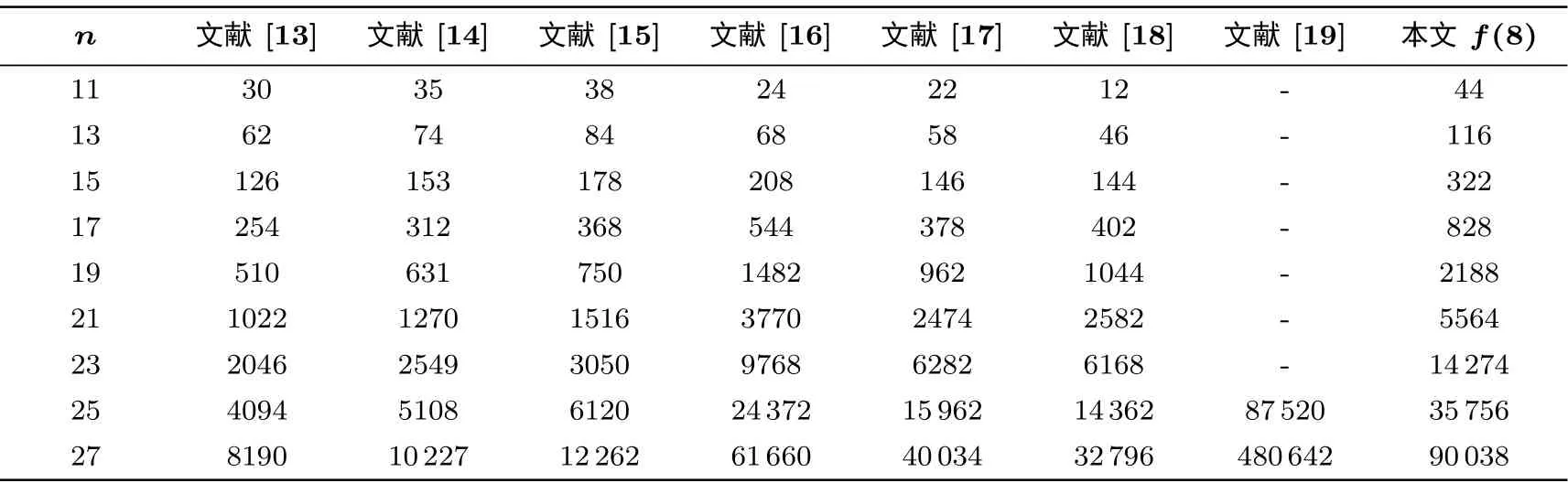
表1 非线性度超过择多函数部分的比较Table 1 Comparison of part of nonlinearity exceeding majority function

4.3 代数次数

这里给出了本文构造的f(x) 的代数次数的分析， 结果表明在某些情况下代数次数可以达到n-1.

定理3 式(8)中函数f(x) 的代数次数满足:

证明: 式(8)中布尔函数f(x) 可表示为f(x)=F(x)+R(x)， 其中

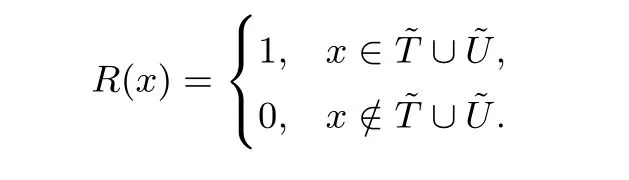
由于wt(R) = 2|～T| 为偶数， 根据式(2)可知deg(R)≤n-1.R(x) 的代数正规型中n-1 次项x1x2···xn/xt(1≤t ≤n) 的系数等价于集合～T和～U中满足xt分量为0 的向量个数N(mod 2). 根据向量x生成轨道的定义可知，x的每一个分量元素都会在位置t出现， 则

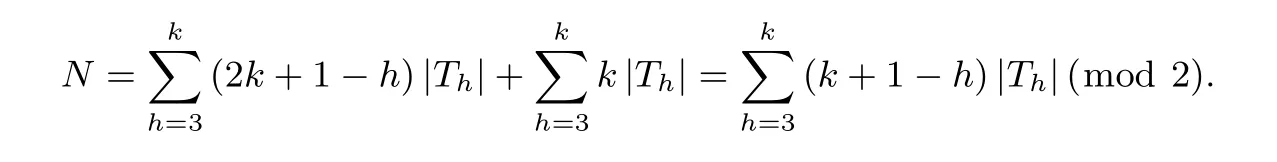
若N=1(mod 2)， 则有deg(R)=n-1; 若N=0(mod 2)， 有deg(R)＜n-1.

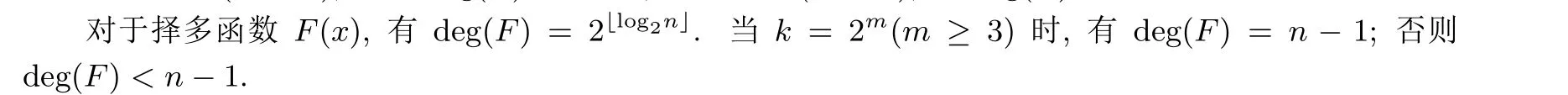
根据上述分析可知， 若满足k= 2m(m ≥3)，N= 0(mod 2)， 或2m-1+1≤k ≤2m-1，N= 1(mod 2)， 则有deg(f) =n-1; 若满足k= 2m(m ≥3)，N= 1(mod 2)， 或2m-1+1≤k ≤2m-1，N=0(mod 2)， 则有deg(f)≤n-2.

利用式(7)给出的|Th| 计数公式， 可计算出5≤k ≤25 范围对应的N的值， 再结合定理3 可得到式(8)中的f(x) 对应的代数次数， 这里给出了5≤k ≤25 范围内式(8)中的f(x) 对应的代数次数:

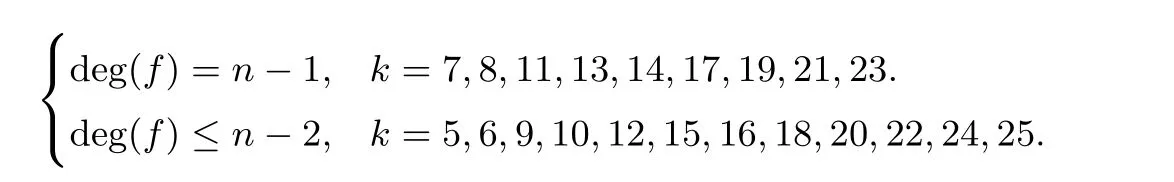
4.4 抵抗快速代数攻击的能力

布尔函数f(x) 的代数免疫度达到了最优， 但并不能说明其具有抵抗快速代数攻击的能力. 一个著名的程序是Simon Fischer 程序， 它可以评估一个函数抵抗快速代数攻击的能力. 在运行Simon Fischer 程序时， 需要函数的真值表和输入n，e，d， 输出将显示满足gf=h， deg(g)+deg(h)＜n的非零函数g和h的解的个数， 其中deg(g)=d， deg(h)=e. 受计算资源限制， 现有文献对布尔函数抵抗快速代数攻击能力的分析通常在小变元范围内进行. 本文为了检验当n= 11，13，15 时式(8)中的f(x) 抵抗快速代数攻击的能力， 对满足d ≥「n/2+d ＜n的e和d的组合， 利用计算机执行了Simon Fischer 程序， 实验结果表明， 当n= 11，13，15 时， 不存在e+d ＜n-1 的(e，d) 组合， 仅存在e+d ≥n-1 的(e，d) 组合.因此， 对于n=11，13，15， 有FAI(f)=n-1. 即本文构造的函数至少在n=11，13，15 时， 抵抗快速代数攻击的能力达到了几乎最优.

5 结论

自从2007 年以来， 如何构造具有最优代数免疫度的奇变元旋转对称布尔函数一直是很多学者所关注的问题， 而如何提高该类函数的非线性度是研究的难点之一. 文献[19] 在变元个数大于23 时提升了现有同类构造的非线性度， 本文在变元个数小于等于23 时提升了现有同类构造的非线性度. 此外本文构造的函数的代数次数在某些情况下能达到平衡函数的最高代数次数n-1， 并且经实验验证构造的函数在n=11，13，15 时， 还具备几乎最优的抵抗快速代数攻击的能力. 本文的构造可以推进对安全性和计算效率要求较高的密码算法中的布尔函数的理论研究， 并为密码算法(特别是需要使用小变元布尔函数的轻量级密码算法) 的设计提供了更多可供选择的布尔函数.