基于分布式PI 的2 阶时延多智能体系统一致性控制
2022-09-07张安通强以铭
王 琦 ,郭 飞 ,张安通 ,郭 煜 ,强以铭
(1.中国船舶科学研究中心,江苏 无锡,214082;2.深海技术科学太湖实验室,江苏 无锡,214082;3.上海机电工程研究所,上海,201109)
0 引言
随着自动控制技术和人工智能技术的快速发展,多智能体系统受到了越来越多研究者们的关注,也逐渐成为人工智能领域的研究热点。多智能体系统由一定数量的智能体构成,通过智能体间的相互协同完成共同的任务。多智能体系统不仅可以提高工作效率,而且易于拓展,可靠性高,在无人艇集群水上作业、无人机空中编队控制、卫星组网通信以及多机器人合作等领域应用广泛。其中,多智能体系统的一致性是指各智能体的状态最终趋于一个相同的值,也是多智能体系统研究中的关键问题[1-6]。
由于通信带宽是有限的,在实际多智能体系统中总是不可避免地存在时延。针对含有时延的多智能体系统,研究者们也进行了相应的研究。通过采用时域的方法,张庆杰等[7]针对具有通信时延的2 阶多智能体系统的平均一致性问题,构造Lyapunov-Krasovskii 泛函得到了系统稳定判据,并引入了自由权矩阵来降低保守性,通过求解线性矩阵不等式(linear matrix inequality,LMI)获得最大的时滞上界。通过采用频域的方法,杨洪勇等[8]针对具有通信和输入时延的含领导者的多智能体系统,运用频域控制理论和Nyquist 稳定性定理,给出了只和输入时延相关的一致性条件。Park 等[9]针对具有通信时延和干扰的离散时间的多智能体系统提出了一种新型一致性算法。Savino 等[10]研究了在切换拓扑结构下具有时变时延的多智能体系统的一致性问题,采用具有不确定转换率的马尔可夫跳变对拓扑变化进行建模。Kaviarasan等[11]研究了存在概率时变时延的不确定非线性多智能体系统的一致性问题,将概率时变时延等价转换为具有随机参数的确定性时变时延。Tan 等[12]针对一类具有时滞的离散时间异构多智能体系统的一致性问题,提出了一种预测方案,通过使用接收到的智能体的过时信息来主动补偿延迟,并设计了一种具有状态预测功能的新型分布式协议,给出了系统达到一致的必要和/或充分条件。Ji 等[13]研究了异构多智能体系统在输入时延影响下的一致性问题,设计的一致性协议考虑了智能体之间的共存合作和竞争互动关系,给出的结论表明系统一致性的实现与系统控制参数、代理的度数和输入时间延迟有关。
针对多智能体系统外部有扰动的情况,相关学者也进行了大量的研究。Mondal 等[14]针对异构高阶非线性多智能体系统提出了一种鲁棒的一致性控制器,提出了一种基于有限时间扰动观测器和滑模控制的分布式一致性协议。Elahi 等[15]针对有外部干扰、通信时延和随机丢包的离散时间多智能体系统进行了分布式一致性控制,以线性矩阵不等式给出了充分条件。Ramya 等[16]通过使用基于干扰抑制和Smith 预测方案的反馈控制器设计了一种新型的一致性控制策略以解决多智能体系统的鲁棒一致性问题。王和等[17]针对2 阶多智能体系统的一致性问题,考虑了在有向通信拓扑结构下存在不匹配扰动的情况,还考虑了有领导者跟踪一致性问题以及无领导者一致性问题。姚辉等[18]研究了在有障碍物和外部扰动的情况下多智能体系统的编队跟踪和避障问题,设计了基于目标跟踪优先级的持续跟踪控制策略,以及基于人工势场法的避障控制协议,并根据自抗扰理论设计包含扰动补偿项的编队跟踪控制器;研究了2 阶多智能体系统的编队问题,采用自抗扰理论和一致性方法提出了包含扰动补偿项的编队跟踪控制协议,并给出了充分条件[19]。葛志文等[20]研究了存在外部扰动和执行器故障的多智能体系统的容错一致性算法,提出了一种基于自适应滑模的算法,相比传统算法,其误差收敛速度更快,容错控制效果更好。
上述研究分别针对具有通信时延和扰动的多智能体系统进行研究,给出了系统实现一致性的条件,但是在实际应用中,可能同时存在通信时延和扰动的影响。Dong 等[21]研究了具有一般线性动力学特性和切换有向拓扑结构的多智能体系统的时变编队分析和设计问题。Yu 等[22]针对高阶多智能体系统的鲁棒H∞编队跟踪问题,同时考虑了具有外部干扰和时变时延,其中编队可以通过指定的分段连续可微向量来定义。
同时,由于比例-积分-微分(proportionalintegral-derivative,PID)控制器研究较为成熟,具有诸多优点,因此有研究者将PID 应用到了一致性控制协议中。Lombana 等[23]分别针对同构和异构系统的一致性问题,使用适当的状态转换和Lypunov函数证明了2 种情况下控制策略的收敛性。李浩亮等[24]针对线性多智能体系统一致性问题,提出分布式PID 控制协议,证明了系统的一致性与增益矩阵和PID 参数有关。但以上文献都没有考虑通信时延和扰动对系统一致性的影响,工程应用性不强。基于以上文献,针对含有通信时延和扰动的2 阶多智能体系统,文中提出了一种基于分布式PI 的控制协议,运用图论、矩阵论和李雅普诺夫稳定性理论的知识,构造具有三重积分项的Lyapunov-Krasovskii 泛函,给出了系统实现渐近稳定的充分条件,降低保守性,最后通过仿真验证了该控制协议的正确性和有效性。
1 问题描述
为了方便描述多智能体系统,引入图论。多智能体系统可以用图论描述为G=(V,E,A),其中:V={1,2,···,N}为一系列节点,表示多智能体系统中的每个智能体;E⊆V×V为每个智能体之间的有向边,表示为eij=(i,j),其中i是j的父节点,j是i的子节点;A=(aij)N×N表示邻接矩阵,当且仅当有向边eji=(j,i)∈E时,aij=1,否则,aij=0。Ni={j∈V,(j,i)∈E}称为节点i的邻居集。图论G的拉普拉斯矩阵L=(lij)N×N定义为

在实际工程应用中,如多无人艇/机编队、机器人协同作业等都可以看作是2 阶多智能体系统。该系统由N个智能体构成,每个智能体的动态特性为
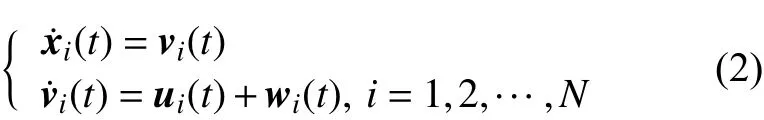
式中

分别表示第i个智能体的位置状态、速度状态、控制协议和非零扰动,n为状态向量的维数,且wi(t)∈L2[0,∞)。
定义1:对任意初始状态值,当且仅当下式满足:

那么含扰动的2 阶多智能体系统(2)达到了一致性。
假设1:对于2 阶含扰动的多智能体系统(2),假设各智能体间的通信拓扑结构G包含一个有向生成树。
在给出主要结论之前,首先给出2 个矩阵论中的引理。
引理1:对于任意常正定矩阵M和标量τ>0,满足不等式
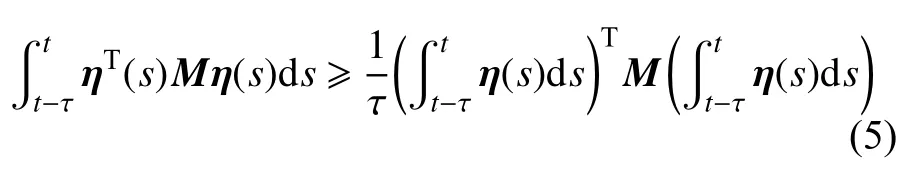
引理2:对于任意常正定矩阵M和标量τ>0,满足不等式

2 主要理论
为了实现该多智能体系统的一致性,根据智能体自身及其邻居状态设计的分布式PI 控制协议为

式中:α,β,ki为控制参数;τ (t)为时延。
同时考虑常数时延和时变时延2 种情况。首先考虑时延为常数的情况,即0<τ(t)=τ ≤d,d为时延的上界。

令

则式(8)可写成

其中,L为2 阶多智能体系统(2)的拉普拉斯矩阵。
令

则可以得到

其中,

如果随着时间的推移limt→∞ξ(t)=0,也就是limt→∞(zi+1(t)−z1(t))=0,limt→∞(xi+1(t)−x1(t))=0,limt→∞(vi+1(t)−v1(t))=0,i=1,2,···,N−1,可以得到z1(t)=z2(t)=···=zN(t),x1(t)=x2(t)=···=xN(t),v1(t)=v2(t)=···=vN(t),即多智能体系统实现了一致性,将原多智能体系统(2)的一致性问题转换为了误差系统(13)的稳定性问题。
定理1:在假设1 满足的条件下,采用控制协议(7),其中时滞为常数0<τ ≤d,如果存在正定矩阵P,Q,R和W,满足下面的线性矩阵不等式

式中,χ=BTP+PB+Q+BTRB−R/d。那么2 阶含扰动常数时延多智能体系统(2)能够实现一致性。
证明:针对转换后的系统(13)构造Lyapunov-Krasovskii 候选泛函
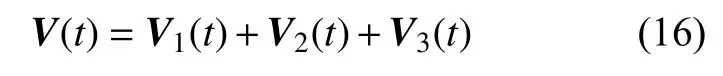
式中

由于P,Q,R可知,构造的Lyapunov-Krasovskii候选泛函是正定的,即V(x)>0。
对其求导可得



整合式(18)~式(22),可得

接着,考虑时延为时变的情况,时变时延τ(t)满 足0<τ(t)≤d,≤d1<1,令xi(s)ds,则将控制协议(7)代入系统方程(2),通过类似的降阶变换可将原系统转换为

式中,B,C,D,ξ 的定义和式(13)一致,可得到推论1。
推论1:在假设1 满足的条件下,采用控制协议(7),其中时变时滞0<τ(t)≤d,≤d1<1,如果存在P,Q和R,满足下面的线性矩阵不等式
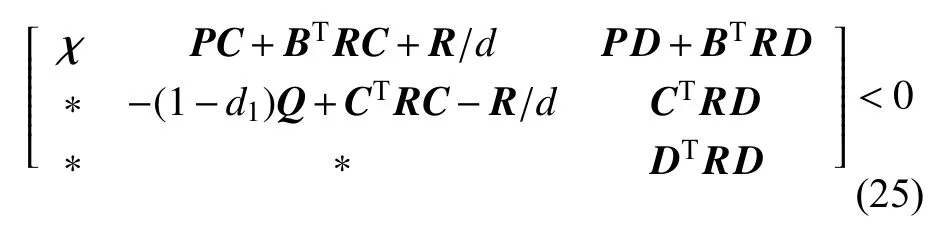
式中,χ=BTP+PB+Q+BTRB−R/d。那么2 阶含扰动时变时延多智能体系统(2)能够实现一致性。
证明:与定理1 的证明类似,在此不再赘述。
在定理1 和推论1 的证明过程中,构造的Lyapunov-Krasovskii 泛函包含了一重积分和二重积分项,如果在Lyapunov-Krasovskii 泛函中加入三重积分项,可以降低系统的保守性,进而得到定理2。
定理2:在假设1 满足的条件下,采用控制协议(7),其中时滞为常数τ,如果存在P,Q,R和W,满足下面的线性矩阵不等式

其中

那么2 阶含扰动常数时延多智能体系统(2)能够实现一致性。
证明:针对转化后的系统(13)构造Lyapunov-Krasovskii 候选泛函

式中

由P,Q,R,W可得构造的Lyapunov-Krasovskii候选泛函为正定,即V(x)>0。对其求导可得
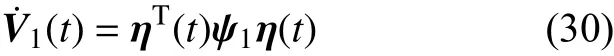
其中

其中


为了实现系统的H∞一致性,即系统渐近达到一致性,且存在一个常数γ>0,使得在任意初始条件下,对于所有的非零扰动w(t)∈L2[0,∞),都有可得到推论2。
推论2:在假设1 满足的条件下,采用控制协议(7),其中时滞为常数τ,如果存在P,Q,R和W满足下面的线性矩阵不等式

其中,
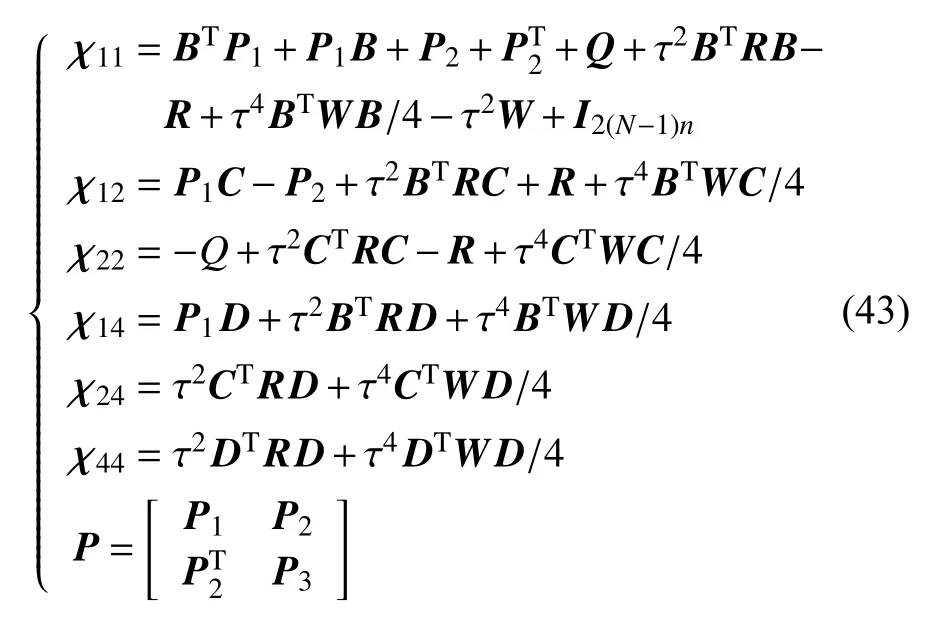
那么2 阶含扰动常数时滞多智能体系统(2)能够实现H∞一致性。

那么

当满足ϕ1<0时,可得

3 数值仿真
考虑通信拓扑结构如图1 所示的多智能体系统,系统中有6 个智能体,编号为1~6,从图1 中可以看出,该拓扑结构含有一个有向生成树,其中节点1 为根节点,从节点1 到其他任意一个节点均有一条有向路径,满足假设条件1。

图1 多智能体系统通信拓扑结构图Fig.1 The communication topology graph of the multiagent system
该系统的外部扰动为

选择参数α=1,β=2,给定时变时延为τ(t)=0.02|cos10t|,运用定理2,通过Matlab 中的LMI 工具箱求得可行解P,Q,R和W,并画出系统中各智能体的状态曲线xi1(t),xi2(t),vi1(t),vi2(t),如图2所示。

图2 多智能体系统状态曲线Fig.2 Curves of state of the multi-agent systems
从图2 可以看出,随着时间的推移,在存在有界外部扰动和时变通信时延的情况下,该多智能体系统的位置状态和速度状态曲线在大约12 s 左右时逐渐达到一个相同的值,从而验证了提出的分布式PI 控制协议可以实现2 阶多智能体系统(2)的一致性,验证了定理2 的正确性和有效性。
4 结束语
针对2 阶时延多智能体系统的一致性问题,同时考虑了外部扰动的影响,采用了分布式PI 控制策略,对该2 阶多智能体系统进行状态转化,从而将原系统的一致性问题转换为新系统的稳定性问题。运用李雅普诺夫稳定性理论对新系统的稳定问题进行分析,构造新型的Lyapunov-Krasovskii候选泛函,给出了新的系统实现稳定性的充分条件,也就是原多智能体系统实现一致性的充分条件。同时,在构造的Lyapunov-Krasovskii 泛函中加入三重积分项,从而减少所得充分条件的保守性。文中结论表明,系统的一致性和控制协议的参数、系统的通信拓扑结构以及时延的上界有关。最后,通过数值仿真对得到的定理和推论进行验证。后续可将文中结果拓展到线性[25]和异构[26]多智能体系统中。
