基于深度学习的微生物高阶逻辑关系分析方法

刘芃兰，孙硕男

（辽宁工程技术大学电子与信息工程学院，葫芦岛 125105）

0 引言

整个生物圈存在着多种多样的微生物，从海洋湖泊、土壤大气到人体的口腔肠道都有微生物的存在。在自然界，不同类群的微生物能在多种不同的环境中生长繁殖，它们彼此联系、相互影响。微生物复杂的生命活动和相互作用对于微生物群落的动态和功能起着重要的作用。

越来越多的证据表明物种间不仅存在成对的相互作用，也存在诸如循环交叉进食和集体共生等大量的高阶相互作用，这些高阶相互作用不但可以使得竞争网络达到动力学稳定，而且对于研究新物种引进也具有重要意义。Zelezniak 等使用基因组尺度的代谢建模方法，系统地调查了超过800个社区的资源竞争和代谢交换的程度，对于所有可能的两个、三个和四个物种组合的子群落，使用Fisher精确检验来评估共现关系的显著性，从而解释了涉及两个以上物种的高阶相互作用的可能性。Bairey 等通过模拟随机交互作用下群落的动态，发现两两相互作用对增加的物种敏感，而四项相互作用对删除的物种敏感，它们共同产生了物种数量的上限和下限。实验结果进一步表明物种互作通常是以高阶组合的形式发生的，两个物种间的相互作用通常由一个或多个其他物种调节，这些高阶相互作用对自然生态系统多样性十分重要。

传统计算模型大多通过成对关系构建微生物网络。然而，由于微生物关系复杂多变，这种成对网络构建方式可能会遗漏大量高阶相互作用，不能很好地捕捉微生物网络的本质特性。网络基序是一种小巧、重复且保守的生物网络单位，它是一个至少包含三个节点且常常出现的网络子图，在网络中执行各种计算任务，通常被理解为一种高阶功能结构。基于这些网络基序来构建高阶网络结构，有助于微生物高阶关系的挖掘，并促使人们更好地理解微生物的功能。识别网络模块是执行网络分析的重要途径，高模块性表明网络在某些节点组内具有密集连接，并且模块之间的连接稀疏。Girvan 等根据社区具有高内聚、低耦合的属性提出基于中心指数来寻找社区的算法。Benson 等提出张量谱聚类算法，根据网络集群中指定的高阶网络结构，开发多线性谱方法对网络进行聚类。Perozzi 等提出了一种Deep-Walk 模型，该模型通过一种截尾随机游走的均匀采样模型将未加权图转化为线性序列集合，然后利用Mikolov 等提出的跳跃图模型从这些线性结构中学习顶点的低维表示，实验结果表明，该模型在聚类任务中要优于常用的谱聚类和模块度模型。基于微生物的纵向数据，Shen等利用动态贝叶斯模型（DBN）构建微生物的加权有向网络，然后利用加权基序和未加权基序对网络的高阶结构进行分析。聚类结果表明，加权基序可以获得更好的聚类。Yu 等提出了一种基于类内散射矩阵的超图聚类方法，并利用谱聚类来实现社区探索，结果表明该方法在一定程度上可以有效地挖掘微生物的高阶模块。

本文提出了一种基于深度学习的超图聚类模型（hypergraph clustering model based on deep learning,DeepHC），用于挖掘微生物的高阶逻辑关系，该模型基于人体18 个部位的微生物丰度数据，计算满足要求的8种逻辑类型的分布，并选取最普遍的逻辑类型来构建高阶微生物网络。针对简单图聚类方法不能有效挖掘高阶关系，而网络的线性嵌入不适用于复杂非线性关系挖掘的问题，提出了一种基于深度神经网络的超图聚类模型，该模型通过计算偏移正点态互信息矩阵来获得更为准确的网络表示，通过深度堆叠自编码器来获得样本的非线性低维表示，并利用最大模块度聚类来自适应挖掘微生物的高阶模块。与其他方法的对比结果表明，DeepHC 得到的微生物模块具有更好的类内紧凑性和类间分离性，可以作为微生物高阶模块挖掘的有效工具。

1 数据与解决方案

1.1 数据

人类微生物组计划研究了大量的微生物群落数据，可以用来描述与人类相关的微生物群落的生态学特征。本文从HMP 数据库中下载16s RNA 序列数据，并经过Mothur 处理得到了V13高质量文件，涵盖了5个人体区域（Gastrointestinal tract，Oral，Skin，Airways，Urogenital tract）的18 个部位，包括3242 个样本，606 个微生物的丰度数据。Gastrointestinal tract 区域有214 个样本，包含1 个部位Stool；Oral 区域有1807 个样本，包含9 个部位，分别是Attached Keratinized， gingiva，Buccal mucosa，Hard palate， Palatine Tonsils， Saliva， Subgingival plaque，Supragingival，plaque，Throat，Tongue dorsum；Skin 区域有736 个样本，包含4 个部位，分别是Left Antecubital fossa，Left Retroauricular crease，Right Antecubital fossa，Right Retroauricular crease；Airways 区 域 有188 个 样 本，包含1个部位为Anterior nares；Urogenital tract区域有297个样本，包含3个部位，分别是Mid vagina，Posterior fornix，Vaginal introitus。上述数据可以从http://hmpdacc.org/HMMCP/下载。

1.2 解决方案

本文提出的DeepHC 方法包含3 个步骤（如图1 所示）。首先，从微生物丰度数据中计算八种逻辑关系，并提取最多的逻辑类型来构建微生物高阶逻辑网络（如图1 的step1）。其次，构建加权超图模型，并通过超图约简得到微生物的连接网络（如图1 的step2）。最后，提出了一种基于深度神经网络的聚类模型用于微生物模块挖掘（如图1的step3）。

图1 基于DeepHC的高阶逻辑关系分析框架图

2 模型与方法

2.1 高阶逻辑关系提取

不确定性推理已被广泛应用到机器学习、专家系统、智能决策等领域，概率逻辑是一种常用的不确定推理方法，它在原有逻辑研究的基础上进行一些概率推理，将概率论和逻辑表示完美融合。微生物的相互作用是群落结构的驱动因素之一，群落中物种的非随机分布可以用来推断这些相互作用。基于微生物丰度数据，本文将概率逻辑应用到微生物领域，进而挖掘微生物的高阶交互关系。

首先，对微生物的原始丰度矩阵离散化处理。当微生物在样本中的丰度值(,) ＞0，则对应的(,) = 1；否则，(,) = 0，删除∑m(,) ＜4的记录。经过以上操作，可以获得最终的微生物丰度逻辑矩阵。

其次，计算任意三种微生物间的不确定系数(|)、(|) 和逻辑组合谱(|(,))。对于任意随机变量和，(|)的计算方法如下：

其中，()和()分别表示和的独立分布信息熵，(,)表示和联合分布信息熵。由式（1）可知，(|)∈[0,1]，当完全由确定时，(|)= 1；当和完全独立时，(|)= 0。因此，对于任意微生物三元组{,,}，(|)和(|)表示微生物和的个体对微生物的影响， 对应成对关系；(|(,))表示微生物和的逻辑组合对微生物c 的影响，对应高阶关系。本文中，(,)表示微生物和的8 种逻辑组合。本文选择成对关系较弱，而高阶关系较强的三元组，即选择满足条件：{（,,）|（|）＜0.4,（|）＜0.4,（|（,））＞0.6}的所有三元组。然后，统计18个部位中不同逻辑类型下三元组的发生情况，结果如图2所示。

从图2 可以看出有5 个部位（‘Right Antecubital fossa’，‘Left Retroauricular crease’，‘Left Antecubital fossa’，‘Right Retroauricular crease’，‘Anterior nares’）满足要求三元组的总数大于2000，并且这些部位的逻辑类型‘=∧’占据绝对的优势，即当和共同存在时，也存在。因此，基于逻辑类型‘=∧’，利用部位‘Right Antecubital fossa’，‘Left Retroauricular crease’，‘Left Antecubital fossa’，‘Right Retroauricular crease’，‘Anterior nares’中的所有三元组来构建高阶交互关系。

图2 18个人体部位的8种逻辑类型的三元组统计图

2.2 超图构建

图聚类根据节点之间的成对相似性对节点集进行划分。然而，由于微生物的多样性，且多样性的社区很大程度依赖于高阶相互作用的稳定程度，因此研究微生物的高阶相互作用对理解微生物群落的多样性和稳定性具有重要意义。Agarwal 等首先认为聚类问题是超图划分的一个实例，该方法首先利用一个加权图来逼近超图，然后利用谱聚类算法来进行超图的节点划分。Zhou 等将谱图聚类技术推广到超图，提出了一种超图归一化切割准则，得到一种归一化超图切割的聚类算法。

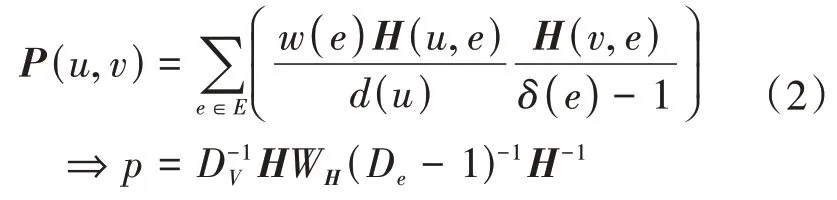
将式（2）与随机游走的公式=对照，可以得到微生物间的连接矩阵：

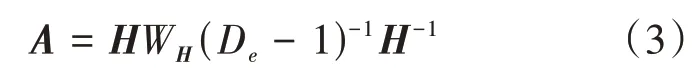
进而，可得超图拉普拉斯矩阵为：=1-DAD。

2.3 基于深度神经网络聚类

基于微生物的拉普拉斯矩阵，传统的谱聚类利用奇异值分解（SVD）和均值可以得到最终的聚类结果。在此过程中SVD 起到降维的作用，通过线性投影将原始表示空间映射到一个新的低秩表示空间。然而，由于实际问题的复杂性，线性投影可能会损失重要的信息。

Tian等利用稀疏自编码器来代替谱聚类中的SVD，取得明显的改进，在此基础上，Cao等提出了一种深度神经网络模型（deep neural networks for learning graph representations,DNGR）来学习图的表示，该模型首先利用随机冲浪模型直接捕捉图形结构信息，然后利用偏移正点态互信息（positive pointwise mutual information,PPMI）模型来增强图的鲁棒性，最后引入叠加去噪自动编码器来提取复杂的非线性特征。DNGR模型在很多聚类和图表示问题中都取很好的效果。尽管DNGR 利用随机冲浪通过转移矩阵的迭代可以挖掘更多的间接交互，然而该过程也在一定程度上增加部分噪声，同时传播参数的选择也增加模型的复杂性。基于以上分析，本文利用PPMI 来增强网络表示，同时利用堆叠自编码器来挖掘样本的低维特征，最后利用均值聚类来计算聚类结果。首先，基于微生物的连接矩阵，计算偏移正点态互信息矩阵PPMI来产生网络表示。PPMI 矩阵构建方法如下：

由式（4）可看出，该计算过程保证PPMI 中元素的非负性。

然后，挖掘微生物的非线性低维表示。利用堆叠自编码器从PPMI 矩阵中产生压缩的、低维的向量表示，这个过程执行了从高维向低维的映射。自编码器包含两个步骤，编码步骤和解码步骤。在编码步骤，函数（·）应用到输入向量，并将其投影到新的特征空间。解码步骤，重构函数（·）从潜在表示空间来重构原始的输入向量。假定：（·）=（+），（·）=（+），其中（·）是激活函数，={,}表示编码步骤的权重参数，={,}表示解码步骤的权重参数，和表示从输入空间到输出空间的线性投影，和表示偏置向量。目标是通过找出和来最小化如下的重构损失函数：

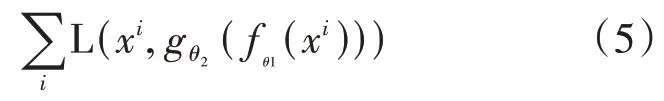
其中，L 表示样本损失函数，x表示第个样本。在这个过程中，激活函数通常用来建模输入空间到输出空间的非线性关系。堆叠自编码器是由多层这样的自编码器组成的深度神经网络，它使用分层的训练方法来提取基本规律，从数据层逐层捕获不同层次的抽象，高层从数据中传递更高层次的抽象。通过执行以上过程，可以得到样本的低维特征表示。

最后，利用最大模块度进行类别数选择。基于堆叠自编码器得到的样本低维特征，利用均值可以得到最终的聚类结果。然而，在此过程中聚类数的选择也是个问题。模块性表现为模块内部的节点比较稠密，模块间的节点比较稀疏。模块性是生物网络的重要特性，研究生物网络的模块性有助于理解复杂的功能和特性。超图模块度是简单图模块度在超图中的推广，令（,）表示顶点和顶点的期望边数，其计算方法如下：

其中，（）表示加权超图中顶点的度。令超图模块化矩阵为A-S，此时，对于任意的聚类结果，可以得到超图的模块度，如下式所示：

其中，表示类别数，（·）表示聚类指示函数，即当顶点和顶点为同一个类别时，（,）=1；否则（,）=0。本文计算不同聚类数下的模块度，并选取最大模块度对应的聚类数。

3 性能与实验分析

3.1 模型评估

3.1.1 RMSSTD指标

RMSSTD是用来衡量聚类结果的同质性，即紧凑程度。它指的是所有类内样本方差的平方根，具体计算公式如下：

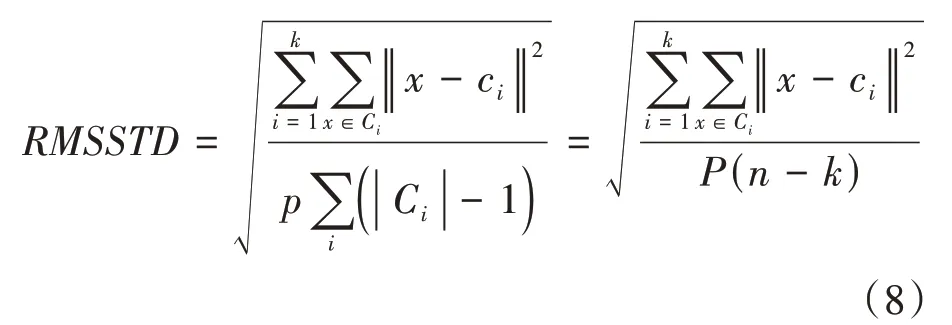
其中，表示类别数，表示样本点，C表示第个聚类的样本集合，c表示第个聚类集合的中心， ||C表示C中样本总数，表示样本的维度。由上式可以看出，越小，类内样本的方差越小，类内样本的紧凑程度越小，聚类效果越好。

3.1.2 RS指标

RS 指标用来评估类间差异程度，即分离程度。它用来衡量一个类别与其他类别的区分度，具体计算公式如下：

3.1.3 CH指标

CH 是一种常用的内部聚类评估指标，由Calinski 等提出，基于类间距离和类内距离的平方和来评估聚类有效性。具体计算公式如下：

3.2 实验设置

为了全面评估模型的性能，实验选择3种对比模型，分别是未加权的超图谱聚类模型（HSC）、加权超图谱聚类模型（HCWS）和基于类内散度的超图聚类模型（HCIS）。对于HSC，超边权重矩阵W为单位矩阵，即所有超边的权重为1，并通过谱聚类得到聚类结果。对于HCWS，超边的权重为逻辑组合谱(|(,))，并利用谱聚类计算聚类结果。对于HCIS，按照论文的原始方法来计算结果。对于DeepHC（本文方法），利用3 层自编码器来生成堆叠自编码器，每层输出样本的维度分别为100、50、10。关于模型的评估，由于所有方法都是基于丰度逻辑矩阵执行的，因此根据和每个模型的聚类结果计算评估指标。此外，为了消除偶然因素对结果的影响，本文将每个实验执行50次，并将评估指标的均值作为最终的结果进行评估。

3.3 结果对比

关于人体的五个位点（‘Left Antecubital fossa’，‘Right Retroauricular crease’，‘Left Retroauricular crease’，‘Right Antecubital fossa’和‘Anterior nares’），基于利用逻辑类型1 提取高阶逻辑关系，将本文模型（DeepHC）与HSC、HCWS和HCIS 的聚类结果进行对比。表1 展示部位‘Left Antecubital fossa’和‘Right Antecubital fossa’，四种计算模型关于三种指标的结果对比。

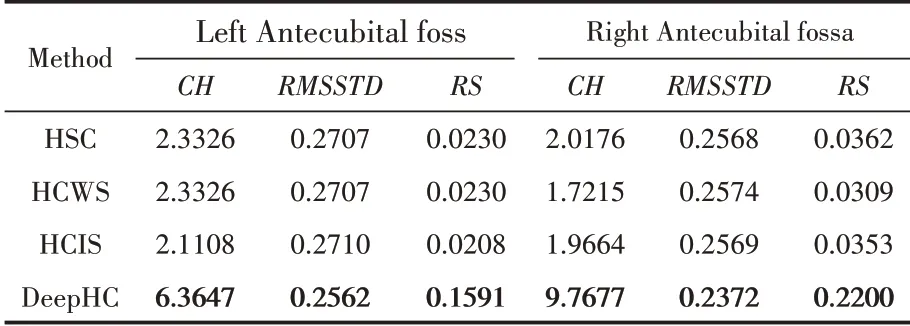
表1 Left Antecubital fossa和Right Antecubital fossa的聚类结果对比

从表1 可以看出，无论是类内紧凑度指标（RMSSTD）、类间差异性指标（RS）还是综合评估指标（CH），本文的模型（DeepHC）关于部位‘Left Antecubital fossa’和‘Right Antecubital fossa’的聚类结果均更好。具体来讲，关于部位Left Antecubital fossa，DeepHC 的RMSSTD 指 标为0.2562，小于其他模型，说明DeepHC 类内样本的紧凑程度更好；DeepHC 的指标为0.1591，远大于其他模型，说明DeepHC 类间差异程度更大；DeepHC 的CH 取值为6.3647，相对于HSC、HCWS 和HCIS 的2.3326、2.3326 和2.1108 分别提升172.86%、172.86%和201.53%，进一步说明DeepHC 具有更好的聚类效果。关于Right Antecubital fossa，DeepHC 的RMSSTD 指标为0.2372，小于其他模型；RS和CH指标分别为0.2200和9.7677，远高于其他模型，进一步说明DeepHC 具有更高的聚类质量。对于剩余的三个部位‘Left Retroauricular crease’，‘Right Antecubital fossa’和‘Anterior nares’，本文将每个部位的指标归一化处理，并将结果以堆叠柱状图的形式展示出来，如图3所示。

图3 位点‘Left Retroauricular crease’，‘Right Antecubital fossa’和‘Anterior nares’的聚类结果对比

由图3 可以看出，对于这三个部位，DeepHC 几乎各个指标都取得了最好的结果。对于部位′Left Retroauricular crease′，如图3（a）所示，DeepHC 的指标最小，对应类内样本的紧凑程度最好；RS指标最大，说明DeepHC类间差异程度更大；同时综合指标HC 也最大，说明DeepHC 取得了最好的聚类结果。关于部位‘Right Antecubital fossa’，也得到了同样的结论。对于部位‘Anterior nares’，DeepHC 除了RS 指标不是最优之外，RMSSTD 和HC 指标都是四个模型中最优的。以上结果表明，DeepHC 可以作为微生物高阶模块挖掘的有效工具。

4 结语

本文提出了一种基于深度学习的超图聚类模型来分析微生物的高阶逻辑关系。与传统的根据微生物成对相关性构建网络的方式不同，本文选择那些两两关系较弱，而联合关系较强的高阶关系进行分析，并统计八种逻辑类型在人体18 个部位的分布，利用出现最频繁的逻辑类型来构建高阶网络。针对一般聚类模型或者不能很好挖掘样本间的高阶关系（简单图聚类），或者仅适应于具有线性关系的样本集合（基于SVD 的谱聚类模型），本文提出了一种基于深度学习的超图聚类模型，该模型通过计算偏移正点态互信息矩阵来增强图的表示，通过深度神经网络来挖掘样本的低维非线性表示，通过基于模块度的K 均值聚类来自适应地选择聚类个数。实验结果表明，本文提出的DeepHC 具有更好的聚类效果，可作为微生物的高阶逻辑关系分析的有效工具。