颗粒团聚对水基铜纳米流体导热系数影响机理研究

王兵兵，王高翔，高轶，徐志明

(东北电力大学能源与动力工程学院，吉林 吉林 132012)

纳米流体是指把金属或非金属纳米粉体分散到水、醇、油等传统换热介质中，制备成均匀、稳定、高导热的新型换热介质[1，2].大量研究表明，纳米流体具有高导热性能，并且提出多种影响纳米流体导热系数的因素，归纳起来主要包括：(1)纳米颗粒的布朗运动及其引起的微观对流[3-6]；(2)纳米颗粒表面形成的致密液体薄膜[7-11]；(3)纳米颗粒的团聚与团聚形态[12-18].

(2)

Xuan等[19]和Murshed等[20]在实验中使用透射电子显微镜(TEM)观察到纳米颗粒的团聚现象.Prasher等[21]和Motevasel等[22]通过实验和假设模型研究提出研究纳米流体导热系数需要考虑团聚作用.Hong等[12]提出纳米流体导热系数与纳米颗粒的团簇密切相关.抑制纳米颗粒团聚对于开发使用纳米颗粒的高效传热流体非常重要.

目前学者对纳米颗粒团聚行为对纳米流体导热性能的影响进行研究，并取得一定成果.Hong和Kim[23]研究表明纳米颗粒的团聚可以显著增加纳米流体导热系数.Prasher[14]和Kang[15]等发现纳米颗粒的团聚使纳米流体导热系数显著提高.并且纳米流体导热系数随颗粒团聚不同形态而发生变化.Sedighi等[16]采用分子动力学模拟分析二氧化硅-水纳米流体热物性参数，发现二氧化硅纳米颗粒团聚后，纳米流体的扩散系数与导热系数增加，但纳米流体的比热没有变化.Lee等[24]采用分子动力学模拟发现纳米颗粒团聚态的导热系数比非团聚态的导热系数高35%.

然而，Wu等[25]通过实验发现在颗粒高体积浓度时颗粒团聚也不会明显提高导热系数.Xuan等[26]研究纳米流体中颗粒随机运动和团聚过程时，研究发现颗粒团聚体的形成降低悬浮颗粒能量传输效率.实验研究中测量纳米流体导热系数时无法避免颗粒沉降的影响，导致目前颗粒团聚对纳米流体导热系数影响的研究结论存在分歧，并且，颗粒团聚影响导热系数的微观机理尚不清楚.本文构建水基铜纳米流体模拟体系，采用平衡分子动力学方法模拟分析纳米流体中颗粒团聚对导热系数的影响规律，通过统计影响导热系数的各项物理参数与颗粒碰撞过程中颗粒间相互作用势能，揭示纳米颗粒团聚行为对纳米流体导热系数影响机理.

1 模拟方法

分子动力学是以牛顿经典力学为基本原理，从分子尺度模拟研究物质的宏观性质或动力学行为，揭示实验难以解释的自然现象或规律[27].与液氩基础流体相比，以水作为基础流体模拟研究纳米流体强化传热机制更加符合实际问题[28-31]，因此，本文选取水作为基础流体，纳米颗粒选为铜颗粒，颗粒粒径为1.5 nm.MD模拟中采用SPC/E水分子模型被证明能够正确获得液态水的许多特性[32]，因此，本文模拟中选用SPC/E水分子模型.为验证模型的合理性，建模时建立了纯水、含有一个铜颗粒体系，含两个颗粒以及四个颗粒体系模型，四个模型如图1所示，模拟盒子三个方向均采用周期性边界条件，模型参数如表1所示.为分析不同颗粒团聚对导热系数的影响，模拟中选取三个不同尺寸模拟体系，分别为39×39×39Å3，78×39×39Å3与78×78×39Å3，相应体系分别含有1个、2个与4个铜颗粒.

表1 模型参数

图1 初始模型

根据已有文献势能与作用参数，模拟体系中粒子间相互作用势能采用L-J作用势能和长程静电作用势能.

(1)

公式中：qi为第i个粒子所带的电荷；rij为粒子i与j之间的距离；ε和σ为势能函数能量参数和长度参数.

粒子间作用势能参数如表2所示[33].不同原子之间势能参数由Lorentz-Berthelot混合法则计算获得，即

采用LAMMPS软件模拟不同体系的演化，粒子初始速度满足高斯分布，模拟时间步长为1 fs，每1 000步输出体系原子坐标与速度.模拟中截断半径选取0.9 nm，长程静电力处理采用PPPM方法，水分子的键长和键角采用SHAKE算法固定[34].体系在NPT系综下运行经过充分弛豫使体系达到平衡状态，随后在NVT系综下运行统计计算导热系数.

本文采用平衡分子动力学方法，应用Green-Kubo公式来计算导热系数，根据文献[35]计算导热系数G-K公式可以写成

(3)

根据文献[36]，热流的公式如下

(4)

公式中：S为应力项作用；ej为势能和动能之和；Fij为原子i对原子j的作用力，rij为原子i和原子j之间的距离.其中ej计算式如下

(5)

公式中：mj为原子j质量；vj为原子j速度；Φij为原子i对原子j相互作用势能.

考虑到势能项(P)，动能项(K)，应力项(S)，从能量角度对导热系数进行分解[31]，导热系数可以写成公式(6)矩阵形式

(6)

2 结果和讨论

2.1 模型合理性验证

为验证模拟设置的合理性，选取文献[36]结果

作为对比，文献中获得纳米流体与纯水导热系数的比值.因此，本文首先对温度300 K下纯水体系的导热系数进行模拟计算，将得到的导热系数与文献[28-31]中结果进行对比，展示在图2中.结果表明纯水的导热系数处于文献获得的结果范围内.进一步验证含铜纳米颗粒模拟体系的合理性，构建含有一个纳米颗粒的铜水纳米流体模型.模拟获得的纳米流体导热系数与纯水导热系数比值，如表3中所示.和文献[37]进行对比，相对误差为2.27%，结果表明本文模拟设置的合理性.这里，选用的纳米流体与纯水导热系数比值为相同质量分数下的实验数据.

图2 300 K温度下纯水模型导热系数与文献对比

表3 纳米流体导热系数与文献对比

2.2 纳米颗粒团聚对导热系数的影响

为提高颗粒热运动与颗粒团聚速率，本文模拟温度设置为363 K高温，颗粒团聚前不同模型导热系数如图3所示.当纳米颗粒的质量分数一定时，实际纳米流体的导热系数应该是确定的.本文建立的相同质量分数纳米颗粒体系，颗粒团聚前，含有1，2与4个纳米颗粒模型的纳米流体导热系数分别为0.97，1.01与1.02 W/(m·K).结果表明含有2个与4个颗粒模拟体系导热系数数值相近，而含一个颗粒模拟体系的导热系数偏低，因此，推断对于MD模拟纳米流体导热系数时采用多个颗粒的模型更合理.

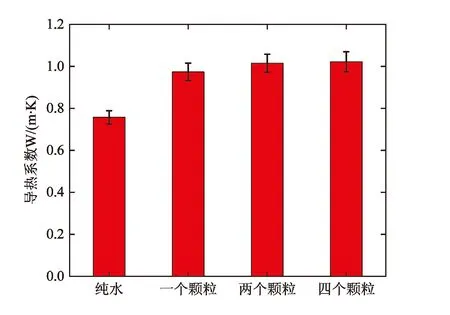
图3 颗粒团聚前不同模型的导热系数

颗粒团聚前后纳米流体的导热系数对比如图4所示，其中四个颗粒模型导热系数只展示了两个颗粒第一次碰撞后的导热系数.在两个纳米颗粒体系中，纳米颗粒团聚后体系导热系数为1.05 W/(m·K)，高于颗粒团聚前导热系数1.01 W/(m·K)，导热系数提高3.96%.对于四个纳米颗粒体系，发生第一次团聚后，体系的导热系数为1.07 W/(m·K)，高于颗粒发生团聚前体系导热系数1.02 W/(m·K)，导热系数增加4.90%，两个模型得到的导热系数系数增长率不同，是由于颗粒团聚程度差异引起的.对于四个颗粒模型，当颗粒再次发生碰撞，体系的导热系数会进一步提高.结果表明，颗粒团聚行为引起纳米流体的导热系数的提升，这与文献[14，15，23，24]结论相一致.模拟中通过增加铜颗粒粒径为2 nm(保持体系中颗粒质量分数不变)，颗粒碰撞后纳米流体导热系数同样升高，验证模拟结论的合理性.相比于粒径为1.5 nm纳米流体，含2 nm粒径的纳米流体具有更大的导热系数.而已有实验[25]得出颗粒碰撞导致纳米流体导热系数降低的实验结果，原因可能是实验中无法避免颗粒团聚沉降引起的.

图4 颗粒团聚前后不同模型体系的导热系数

2.3 颗粒团聚对导热系数影响机理分析

为揭示纳米颗粒团聚对纳米流体导热性能的影响机理，结合公式6对导热系数各项贡献进行统计分析.这里以两个颗粒模型为分析对象，颗粒团聚前纳米流体导热系数与各项贡献如图5所示.在这六个贡献项中，对体系导热系数作用占比最高的应力贡献项(SS，69.42%)，其次是势能贡献项(PP，20.60%)，这两项贡献之和占比为90.02%，动能贡献项(KK)占比为0.56%.其余为势能贡献项、应力项及动能耦合作用部分.

图5 两个颗粒模型的纳米流体导热系数与各项贡献

本文重点分析影响纳米流体导热系数的贡献项占比高的势能(PP)与应力项(SS).图6对比了颗粒团聚前后纳米流体导热系数和各项贡献.颗粒团聚前后对纳米流体导热系数的势能贡献项从0.225 W/(m·K)变化为0.265 W/(m·K)，增加幅度为17.78%.应力贡献部分从0.725 W/(m·K)变化为0.724 W/(m·K)，减少幅度为0.14%.因此，体系势能项的变化是颗粒团聚后纳米流体导热系数增加的主要因素.

图6 颗粒团聚前后体系导热系数和各项贡献对比

为分析颗粒团聚前后体系势能变化，本文分别统计了体系中铜颗粒与水的势能值，结果如图7所示.颗粒团聚前后颗粒势能绝对值从705.72 eV变化到725.09 eV，势能绝对值增加19.37 eV.而水的势能绝对值从1 723.11 eV变化到1 719.91 eV，势能绝对值减小3.20 eV.因此，颗粒碰撞过程中势能变化主要是由颗粒势能的绝对值增加引起的.

图7 颗粒团聚前后体系中铜颗粒与水势能绝对值变化

为分析两个纳米颗粒团聚过程中体系势能变化原因，本文统计了颗粒团聚前后两个颗粒之间的相互作用势能变化，统计结果展示在图8中，负号代表两个颗粒相互吸引.在0 ps～4200 ps区间，两个纳米颗粒相向运动(未发生团聚)，颗粒之间相互作用势能接近0.在4 200 ps～4 240 ps区间内，两个纳米颗粒相对运动到较近距离，颗粒间相互作用势发生变化，两个颗粒在4 240 ps时发生团聚.随后(t>4 240 ps)，两个颗粒团聚为一个稳定状态，此时颗粒间相互作用势能恒定.分析两个纳米颗粒之间相互作用势和体系总势能，可以看出，体系总势能的变化是由于两个纳米颗粒之间相互作用势变化而引起的.即两个纳米颗粒团聚增加了两个纳米颗粒之间相互作用势，导致体系的总势能绝对值增加.

图8 颗粒团聚前后颗粒相互作用势能

两个铜颗粒间作用为短程范德华力，而两个铜颗粒能够相向运动，两个铜颗粒间作用势能接近0如图8所示，因此，一定存在其他强的吸引力作用.由于铜颗粒对水分子有较强的吸引作用，颗粒表面存在明显的水吸附层[7]，本文统计了两个纳米颗粒团聚前距颗粒表面一定距离(0-9 Å)内水分子密度变化，统计结果如图9所示.颗粒近表面处水分子数密度存在两个波峰，表明纳米颗粒周围存在两层明显的水吸附层.这两层吸附层的密度均大于体系平均密度，第一吸附层内水分子密度最高，第一吸附层距颗粒表面距离为5 Å(对应于第一波谷)，第二吸附层距颗粒表面距离为7 Å.

图9 纳米颗粒周围水分子密度分布

为分析水分子吸附层对颗粒相向运动影响，如图9所示，以颗粒与周围一层或两层水吸附层定义颗粒团簇单元，这里第一与第二层分别以距颗粒表面5 Å和7 Å为水分子吸附层的分界.包含一层与两层水吸附层的两个颗粒团簇之间相互作用势平均值计算结果分别为-20 eV和-28 eV，负号表示相互吸引.结果表明，水分子间作用包括长程库仑力作用，包含水吸附层的两个铜颗粒团簇间存在强的吸引作用.因此，颗粒发生相向运动是由于颗粒表面的水吸附层引起的.当颗粒间距离很近时，如图8中子图所示，颗粒间的相互吸引力才对颗粒团聚起作用.综上所述，水基铜纳米流体中铜颗粒表面存在两层致密的水分子吸附层，吸附层间强的吸引作用导致颗粒相向运动并发生团聚.颗粒团聚的发生引起颗粒势能与体系总势能的绝对值增加，从而导致纳米流体的导热系数提高.

3 结 论

本文采用平衡分子动力学方法计算水基铜纳米流体的导热系数，通过对比分析体系的势能、应力、动能及颗粒之间相互作用势，从微观角度揭示了团聚行为对纳米流体导热性能的影响机理.模拟结果表明，采用分子动力学模拟计算较高体积分数的纳米流体时，建立多颗粒模型计算纳米流体导热系数结果更合理.纳米颗粒发生团聚会导致纳米流体导热系数增加，通过分解体系导热系数的各项贡献发现，颗粒团聚后颗粒势能绝对值的增加导致体系势能的增加，是导致纳米流体导热系数增加的物理机理.此外，模拟发现铜纳米颗粒表面存在致密的水分子吸附层，颗粒水吸附层之间强吸引作用是颗粒相向靠近与发生团聚的驱动力.而当颗粒较近时，颗粒间的吸引力才对颗粒碰撞起作用.