双肋椭圆扭管管内传热与流阻特性分析及其多目标结构优化
2022-09-06刘必伟师春雨刘志春
刘必伟,师春雨,刘 伟,刘志春
(华中科技大学能源与动力工程学院,湖北 武汉 430074)
随着经济与科技的发展,世界范围内的能源消耗水平亦日益增加,因能源产生的社会与经济问题也随之加剧.换热器作为能源化工领域的重要器件,对其进行强化换热的研究对缓解能源消耗具有巨大的意义.换热器的强化换热研究主要集中在新型换热器器型开发与强化换热管研究.对于换热管,强化换热手段包括异形换热管设计——如三叶管、微肋管,与插入扰流元件,如弹簧纽带、锥形片.
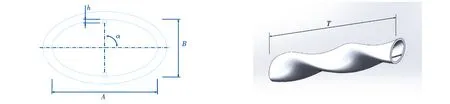
Bhadouriya等[1]利用实验和数值模拟研究了方形截面扭管内空气的传热与流阻特性.分别研究了不同扭曲比的换热管在雷诺数100至100 000时的情况,结果显示方形扭管比圆管拥有更好的传热性能,并且更适用于层流,当Re=3 000时,扭曲比为2.5的方形扭管能获得最好的综合效果.Eiamsa-ard等[2]通过数值模拟的手段探究了以水为工质湍流情况下的三头扭管与三叶形扭带组合的强化换热管,结果表明,由于二次流的存在,扭管与纽带结合具有更好的传热性能.Zambaux等[3]研究了内外壁连续交替变形的同轴管的热工水力性能,相比光滑圆管,连续变化的壁面对流体的扰动致使换热管具有更佳的性能,并且得出外壁和内壁之间具有八分之一波长的相移值时,综合性能可提高43%.Samruaism等[4]通过实验和数值模拟研究了水在湍流情况下三角形截面扭管与双弹簧纽带组合强化管的特性,并且研究了扭绞比与努赛尔数和流动阻力的影响,确定了4 500 以往学者对扭曲管的研究多集中于截面形状、插入物等强化换热手段,而少于针对椭圆管进行壁面处理的研究.本文提出了一种具有两根对称排布的矩形内肋的椭圆扭管,利用数值计算方法,分析了其在雷诺数为5 000~50 000情况下的努赛尔数Nu、阻力系数f、流动换热综合评价指标PEC以及速度-温度梯度场协同角β等指标.对比研究了该换热管与普通椭圆扭管和圆管的差异,以及矩形肋排布角度α对其流阻与传热性能的影响.最后利用NSGA-II算法对其进行截面参数优化,以努赛尔数增长率与阻力系数增长率为优化目标,通过TOPSIS方法选择出了最佳结构参数. 在研究中,双肋椭圆管的横截面示意图与三维模型如图1所示.结构参数包括(1)管长L;(2)长半轴a;(3)扭矩T;(4)肋高h;(5)双肋与长轴夹角α.为了比较强化传热管的性能,论文比较了没有肋的椭圆管以及相同周长的圆管,其中基准圆管尺寸为(φ25×2.5)mm,椭圆管周长与圆管一致. 图1 双肋椭圆扭管平面(左)与三维(右)示意图 本文首先对比研究了双肋椭圆扭管、椭圆扭管、光滑圆管在Re=5 000~50 000情况下的流动与传热特性.换热管L均为1 000 mm;两根椭圆管a=13 mm、b=6.45、T=150 mm,其中双肋椭圆管h=1 mm、α=90°.其次,研究了α由0°变化至90°时双肋椭圆扭管各项流动传热特性指标的变化情况.最后以努赛尔数增长率与阻力系数增长率为目标,利用NSGA-Ⅱ算法与TOPSIS方法选取双肋椭圆管在截面参数a∈(12 mm,14 mm),α∈(30°,90°)时的最佳结构. 为了简化计算过程,对计算目标的数学模型进行合理简化假设:(1)不考虑重力;(2)工质不可压缩;(3)流体连续;(4)无滑移壁面条件;(5)不考虑辐射. 流体在管内对流换热时满足的控制方程如下所示. 质量守恒方程: (1) 动量守恒方程: (2) 能量守恒方程: (3) 公式中:μeff为有效动力粘度等于层流与湍流动态粘度之和;λeff为有效导热系数,λeff=λl+μtcp/Prt,下标l与t分别代表层流与湍流. 选用剪切应力输运模型(k-ωSST)作为湍流模型,其方程如下所示. (4) (5) 公式中:Pk,μt,S可由下列方程得到: (6) (7) (8) 公式中:F1,F2为混合因子,所有系数通过φ=φ1F1+φ2(1-F1)得到,下标1代表k-ω模型,2代表k-ε模型.β*=0.09,φ1=5/9,φ2=0.44,β1=3/40,β2=0.082 8,σk1=0.85,σk2=1,σω1=0.5,σω2=0.856. 通过计算之后,得到对流换热过程中的速度、温度以及压力等参数分布,之后对数值模拟结果进行处理.计算过程中,对数平均温差ΔT、对流换热系数h、等效水利直径Dh、雷诺数Re、平均努赛尔数Nu、阻力系数f与速度-温度梯度场协同角β的定义如下所示. (9) Δp=pin-pout, (10) (11) (12) (13) (14) (15) (16) 计算模型采用ANSYS CFD ICEM对目标模型进行网格划分.近壁面划分了十层边界层网格,保证y+~1,确保边界层计算准确.对光滑椭圆扭管进行了网格独立性验证,划分了网格数分别为1 406 784、3 213 850、5 872 922的三套网格,计算其在Re=20 000时的努赛尔数Nu与阻力系数f.网格数为1 406 784的模型较于网格数为3 213 850的模型的Nu与f的误差分别为0.7%与-0.6%;网格数为3213850的模型较于网格数为5 872 922的模型的Nu与f的误差分别为0.01%与0.3%,因此认为网格数不少于321万时满足网格无关性. 管内流动工质为水,物性不随温度变化;入口条件为速度入口,工质入口温度为297 K,管壁为定壁温345 K;出口条件为压力出口.压力与速度耦合采用SIMPLE算法,动量、能量方程采用二阶迎风离散方法,当能量方程的残差小于10-8,连续性方程的残差小于10-4,其余方程的残差小于10-6时认为计算收敛. 选用k-ωSST作为湍流模型,对光滑椭圆扭管、光滑圆管进行数值模拟.为保证湍流充分发展,选取距入口400 mm至600 mm段流域计算其Nu与f.并将椭圆扭管的计算结果与Gao等的实验结果[6]对照;圆管的计算结果与公式(17)、公式(18)对照,经验公式分别来自Gnielinski[7]与Filonenko[8].结果如图2所示.数值计算所得结果与实验或经验公式的误差均在可接受范围内.其中,光滑椭圆扭管的f同Nu与实验经验式的最大偏差分别为-18.14%与-10.9%,最小偏差分别为-2.23%与-2.03%;光滑圆管的f同Nu与实验经验式的最大偏差为3.53%与13.60%,最小偏差分别为1.81%与-0.42%,因此认为该湍流模型具有较高的准确性. 图2 实验验证 (17) f=(1.82lgRe-1.64)-2. (18) 双肋椭圆扭管与椭圆扭管在Re=20 000时,距入口500 mm处的截面温度、速度分布与流线图与涡量云图如图3、图4、图5所示.从图3可以看出相较于椭圆扭管,双肋椭圆扭管的截面温度分布更加均匀,平均温度更高.由于扭管截面随主流方向发生扭转,扭管具有更大的横向速度,破坏了边界层,增强了边界层与流体域中心区的换热.从图4可以看出,双肋椭圆扭管具有更大的横向速度,并且在双肋处分别出现了两个明显的纵向涡.双肋椭圆扭管由于肋的存在,破坏了边界层的同时,强制改变了流体横向运动的方向,在壁面附近造成了二次流,使得流体向中心流域冲击,增强了流体在温度梯度方向上的速度. 图3 Re=20 000时双肋椭圆扭管(左)与椭圆扭管(右)在L=0.5 m处温度云图 三种换热管的Nu随Re的变化情况如图6(b)所示.可以看出,在不同的雷诺数下,双肋椭圆扭管、椭圆扭管的Nu均高于圆管.从图4中,肋的存在使得换热管内有更大的纵向涡量,纵向旋流使得冷热流体混合,增强壁面热量向主流中心扩散,因此较于另外二者,其拥有更好的换热性能. 三种换热管的流阻特性随Re的变化情况如图6(a)所示.由于截面扭转,椭圆扭管的流体具有横向速度,对壁面的冲击造成了流动损失,因此比圆管具有更大的阻力.从图3可以看出,双肋管中,内肋强制改变了流体横向的运动方向,进一步提高了流动损失,阻力系数最大.三者的阻力系数f均随Re的增大而减小,并且变化逐渐趋于平缓.这是由于低雷诺数时壁面边界层较厚,粘滞力对阻力的影响较大,当Re升高,湍流度提高,边界层影响减小,因此阻力系数变化趋势减缓. 图6 双肋椭圆扭管、椭圆扭管、光滑圆管流动换热特性:(a)f;(b)Nu;(c)PEC;(d)β 为考虑综合椭圆扭管的传热和压降性能,以相等功耗下传热膜系数为基础,前人定义了流动换热综合指标[9]: (19) 公式中:下标0代表光滑圆管. 两种强化换热管的流动换热综合指标图6(c)所示.可以看出,双肋椭圆扭管相较于光滑椭圆管具有更好的综合性能.Re小于15 000时,二者能获得更显著的综合换热性能,当雷诺数升高,管的结构对综合性能的影响逐渐减小,当Re大于20 000时,光滑椭圆扭管综合性能接近光滑圆管. 三种换热管在不同雷诺数下的平均速度-温度梯度场协同角β如图6(d)所示.场协同原理是由过增元[10]首先提出用以描述对流传热中速度场与温度梯度场协同性能的理论.β越小,协同度越大.由于温度梯度主要方向为壁面向主流中心,而无扰动情况下圆管内横向速度低,因而圆管的平均场协同角接近90°.两根椭圆扭管,横向速度使得热量被流体运动带离边界层,故二者具有更小的协同角,双肋造成的二次流,破坏了边界层,强制边界热流体向中心冷流体区域方向冲击混合,因此具有更大的协同度,故其拥有更好的传热效果. 由上述分析可得,双肋导致的二次流使换热管具有更大的协同度,因而具有更强的强化传热性能.本部分研究了双肋的不同布置角度对椭圆扭管的流动传热性能造成的影响.研究了在Re=5 000~50 000范围内,双肋与长轴的夹角α分别为0°、20°、40°、60°、90°时椭圆扭管的流阻与传热. Re=20 000时不同排布角度下的双肋椭圆扭管在0.5 m处的截面温度云图如图7所示.当α由0°变化至90°时,双肋对管内流体扰动的作用区域由长轴两侧逐渐转移至中心流域,当α较小时,长轴两端温度更高,而中心区域温度很低;当α靠近90°,因内肋产生的纵向旋流作用在短轴两侧,壁面热量能很好地传递至中心,因此中心流域平均温度更高,而长轴侧温度更低;当α在60°附近时,扰流作用能够同时作用于长短轴两侧,因此其具有更高的平均温度. 图7 Re=20 000时不同双肋排布角度下双肋椭圆扭管在L=0.5 m处的温度云图:(a)f;(b)Nu;(c)PEC;(d)β 图8展示了不同双肋排布角度下椭圆扭管的努谢尔数Nu、阻力系数f、综合评价指标PEC与速度-温度梯度场协同角β随Re的变化规律.从图中可以看出,当角度从0°变化到90°,扭管的换热性能与阻力系数先增后减,当肋对角为60°时,换热性能最好、阻力系数同时也具有最大的流动传热综合指标. 从图8(d)中显示的不同排布角度下双肋椭圆扭管的管内场协同角的变化规律可以看出,换热管的平均场协同角呈现与Nu相同的变化规律,当α为60°时,协同角最小,说明此时换热管速度与温度梯度协同作用较好.由于椭圆管的截面并非对称,因此肋在不同位置时对管内流场的影响也不尽相同,在60°附近,纵向涡能够有更大的影响区域,因此双肋椭圆管拥有更好的换热性能. 图8 双肋排布角度对椭圆扭管流动换热特性的影响 取两个重要的截面参数长半轴a与双肋排布角度α为设计变量,对双肋椭圆管进行优化.基于工业中常使用的尺寸与上节参数分析的结果,a取值范围为a∈(12 mm,14 mm),α的取值范围为α∈(30°,90°).其余参数L=1 000 mm、T=150 mm、h=1 mm、Re=10 000. 对于换热管的强化换热而言,通常希望在提升其换热能力的同时具有更小的压降,因此以努塞尔数提升率Nu/Nu0最大与阻力系数f/f0最小为优化目标对齐进行多目标优化. 析因实验指将实验所关注的全部实验因素的各水平排列组合成为不同的实验条件,在变量设计范围内,利用析因试验方法得到12个参数组合,对每种组合的换热管进行数值模拟,结果如表1所示. 表1 设计变量及目标函数值 利用响应面分析优化目标与参数之间的关系,得到相应的代理模型.选取二次多项式模型作为代理函数的数学模型,如公式(20)所示. (20) 对试验结果进行拟合,得到响应面如图9所示.图中x轴与y轴分别为长半轴a与双肋排布角度α,z轴则分别为Nu提升率与f提升率.其表达式分别为 图9 代理模型响应面 Nu/Nu0=-16.87+2.591a+0.017α-0.094 07a2-0.000 397 6a*α-0.000 074 27α2. (21) f/f0=-7.57+1.228a+0.008 449α-0.042 72a2-0.000 030 35a*α-0.000 0499 4α2. (22) 多目标遗传算法常用来协调各个优化目标函数的关系,找出使每个目标都尽可能大(小)的解集.本文选用带有精英保留策略的快速非支配遗传算法即NSGA-Ⅱ算法通过代理模型对Nu/Nu0与f/f0进行优化. 在NSGA-Ⅱ算法中,初始种群数为100,最优个体比例为0.45,适应度函数偏差为10-10,迭代200代后停止,最后输出45个Pareto最优解.并利用优劣解距离方法(TOPSIS)对30个最优解进行排序选择,得到结果如图10所示. 图10 Pareto最优解前沿与TOPSIS解 TOPSIS选取的最优参数组合为a=13.44 mm、α=58.5°.该解相较于换热能力提升最大的解,Nu/Nu0降低1.54%、f/f0降低5.21%;相较于阻力系数提升最小的解,Nu/Nu0提升41.01%、f/f0仅提升23.53%.由此可见,TOPSIS选择的参数组合在传热能力提升与降低压降比其他二解更具优势. 本文提出了一种具有两根对称排布矩形内肋的椭圆扭管,对比了其与光滑椭圆扭管和光滑圆管的性能差异;研究了内肋排布角度对其性能影响;最后考虑设计变量截面长半轴a与肋排布角度α,以Nu/Nu0与f/f0为优化目标对其进行优化,利用TOPSIS选择出了最佳参数组合. (1)双肋使椭圆扭管管内流体横向速度更大,纵向涡强度更大,能够破坏边界层,增强壁面附近流体与中心区混合,从而强化传热. (2)在Re=5 000~50 000时:Nu随雷诺数增大而增加,扭管换热能力强于光滑圆管,双肋椭圆扭管换热能力最强;f随雷诺数增大而减小,相同雷诺数下扭管的阻力系数均大于圆管,双肋椭圆扭管具有最大的压降;双肋椭圆扭管的PEC拥有最好的综合性能,最高为Re=5 000时的1.96;双肋椭圆管速度-温度梯度协同效果最好. (3)相同雷诺数下,截面长半轴a=13 mm、h=1 mm时,当双肋排布角度为60°时,双肋椭圆扭管具有最大的平均场协同度与综合性能,当Re=5 000时,PEC可达1.243. (4)多目标优化后,利用TOPSIS在Pareto解集中选择出最终的参数组合.该解相较于换热能力最好的解,Nu/Nu0降低1.54%、f/f0降低5.21%;相较于压降最小的解,Nu/Nu0提升41.01%、f/f0仅提升23.53%.该参数组合下换热管具有较好的综合性能.1 计算模型与验证
1.1 几何模型
1.2数值模型
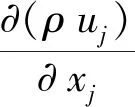

1.3数据处理
1.4 网格独立性验证
1.5 边界条件与模型验证

2 结果分析
2.1 性能分析
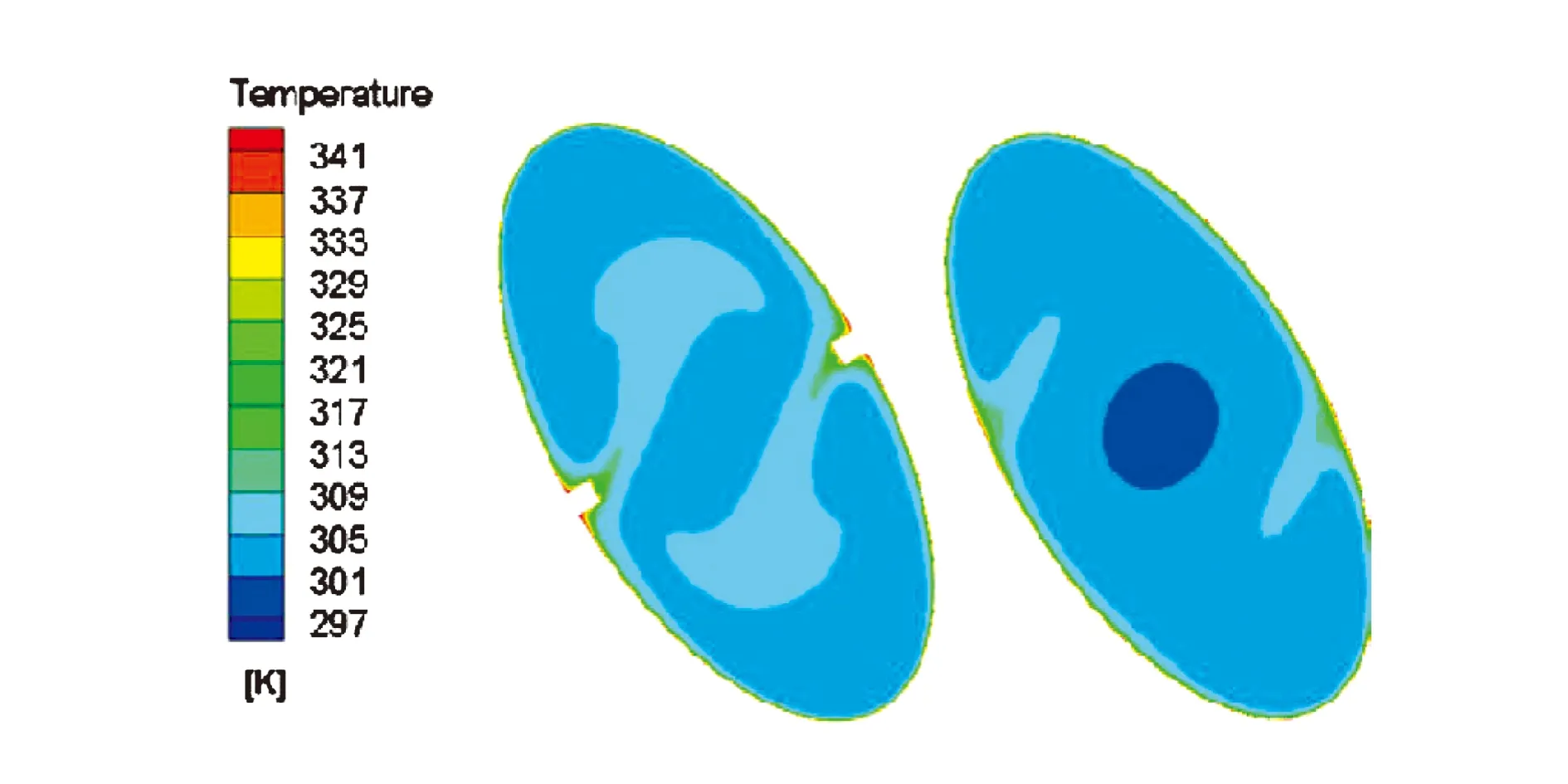
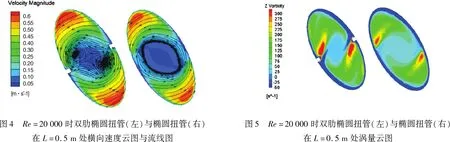

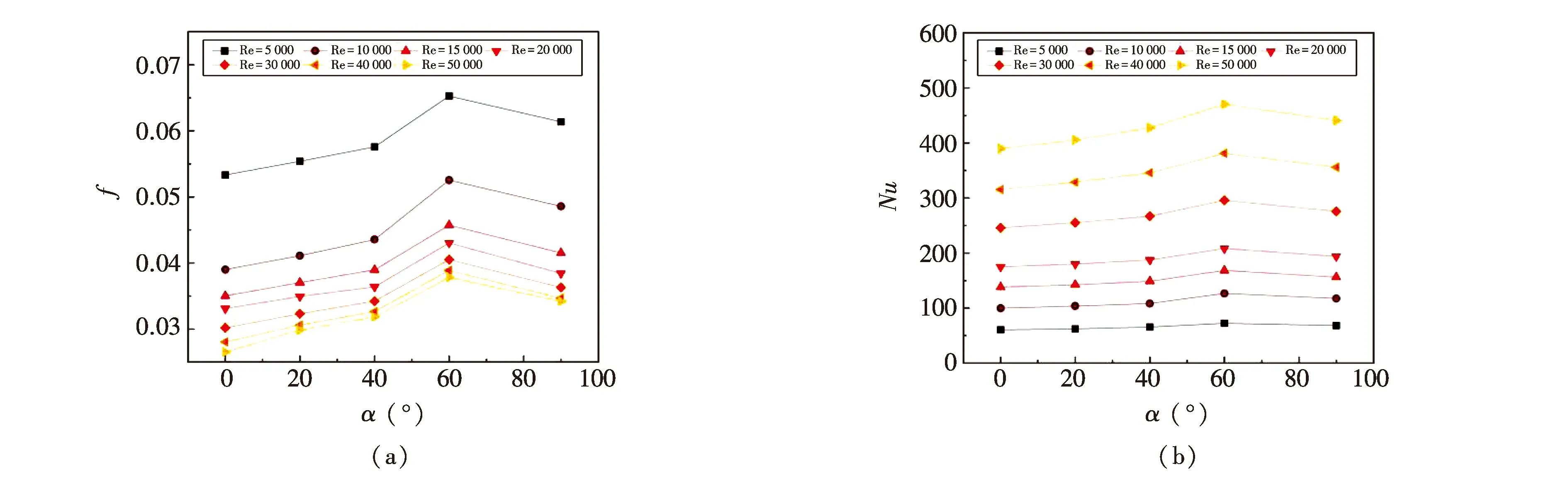
2.2 双肋布置角度对扭管性能的影响


3 结构优化
3.1 设计变量和优化目标

3.2 代理模型

3.3 多目标优化结果

4 结 论
