基于高精度三轴转台的GNSS/INS组合导航姿态性能自动化测试评估方法研究

王剑平，潘树国，高旺，喻国荣，贺留杰，王浩

( 1. 东南大学 仪器科学与工程学院, 南京 210096；2. 东南大学 交通学院, 南京 210096；3. 江苏海洋大学 海洋技术与测绘学院, 江苏 连云港 222005 )

0 引 言

全球卫星导航系统/惯性导航系统(GNSS/INS)组合导航系统，被公认为是目前最优的组合导航形式，因为其较高的抗干扰能力、连续性及可靠性等优势，在军用和民用导航领域得到了广泛地运用[1-6]. 由于组合导航系统评价指标多样且意义不同，类型也随着用途、型号、组合方式的不同而不同，使得系统建设工作具有研制复杂、资源消耗大、使用周期长的特性[7]. 因此，针对GNSS/INS组合导航系统进行性能评估是保证所研制的组合导航系统满足各项性能指标，提高系统可靠性，降低研制技术风险和成本的重要一环[8].

近年来国内外诸多专家学者在导航系统性能评估方面开展了深入研究[9-10]. 伦敦帝国理工大学Umar Iqbal Bhatti 设计了一套组合导航系统仿真平台，用以分析组合导航系统完好性算法性能[11]；王敏[12]提出了采用数理统计法对组合导航系统影响因素进行定性、定量估计的方法，进而开发了组合导航评估系统，并通过室内模拟实验完成评估；卢鸿谦[13]针对SINS/GPS组合导航系统，研究了增强其可靠性、精度、稳定性的方法. 目前，国内在GNSS/INS组合导航系统测试评估技术研究方面，仍存在评价方式过于单一(仅直接评价和数值评价两种，缺乏更具说服力的评价方式)，存在数据自动化处理程度不高等问题. 因此，研究一种面向GNSS/INS组合导航系统姿态性能实时动态(RTK)测试评估新技术，探索组合导航终端产品姿态性能指标评价新方法，提升GNSS/INS组合导航姿态性能测试结果表达的准确性和全面性，实现测试评估流程的自动化，对于推动组合导航终端产品技术优化、建立行业准入机制、促进产业健康发展具有十分重要的意义.

本文依托高精度三轴动态基准仿真转台，针对GNSS/INS组合导航系统姿态性能测试评估，研究了粗差探测与剔除算法、误差计算与精度统计算法以及不确定度分析算法，并研发了具备评估误差动态显示功能的评估软件进行测试. 利用三轴转台姿态模拟仿真功能，设计多转位复合姿态运动测试任务，通过多转位、多姿态且具有重复一致性的测试流程，对GNSS/INS组合导航系统姿态进行针对性评估测试.最后使用实测数据对两类GNSS/INS组合导航终端产品姿态评估结果，与自身技术参数进行了对比，从而验证了本文所提测试评估方法的可行性.

1 测试评估算法

测试评估算法主要包括粗差探测与剔除算法、误差计算与精度统计算法和不确定度分析算法. 数据处理流程为：采用汤普森(Thompson)奇异值剔除法剔除三轴转台异常姿态参考值[14]，随后将其与组合导航设备姿态数据做差，进行误差均值和均方根(RMS)统计，并结合转台基准不确定度进行评价分析，保证测试评估基准的客观可用性.

1.1 粗差探测与剔除算法

由于采集到的转台基准数据中可能包含误差较大的数据，对测试评估的结果影响较大，因此在进行测试之前需要舍弃掉这些数据. 该模块采用Thompson奇异值剔除法对转台基准数据中的粗差项进行探测与剔除. 测试中采集得到n个基准数据X1,X2,X3,···,Xn，为检验数据中是否含有奇异值，先按式(1)计算：

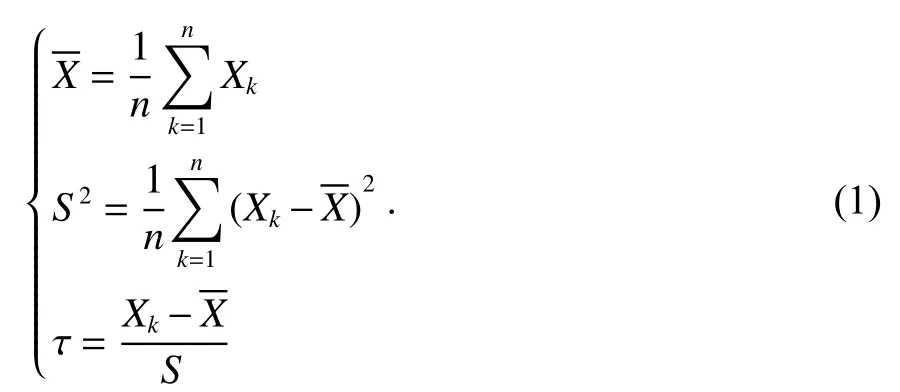
然后将 τ 代入式(2)计算求得统计量

若 |t|＞t(n-2,α) ，则Xk被剔除，否则Xk保留. 其中，t(n-2,α) 为 学生氏t分布分位点，可根据自由度n-2 和显著性水平 α 从学生氏t分布表中查得. 经过上述剔除流程后，可以完成转台基准奇异值数据进行准确的预处理工作，保证转台基准数据可靠性，为提高测试评估结果的可信性奠定了基础.

1.2 误差计算与精度统计算法

经过粗差探测与剔除处理后，对GNSS/INS 组合导航设备和处理后的转台参考基准姿态数据进行做差并进行数理统计. 本文采用RMS误差值来评价组合导航姿态动态性能指标，包括：方位角精度、俯仰角精度、横滚角精度. 以方位角精度评定方法为例，首先计算出方位角误差均值，如式(3)所示：

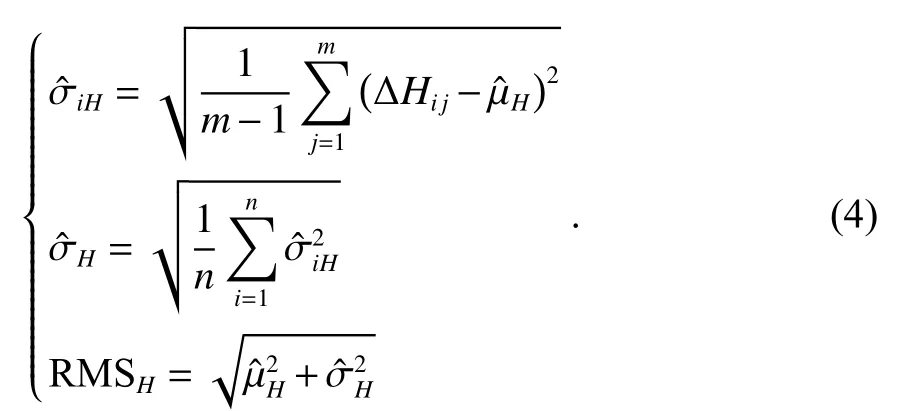
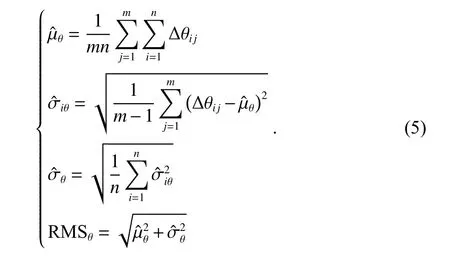
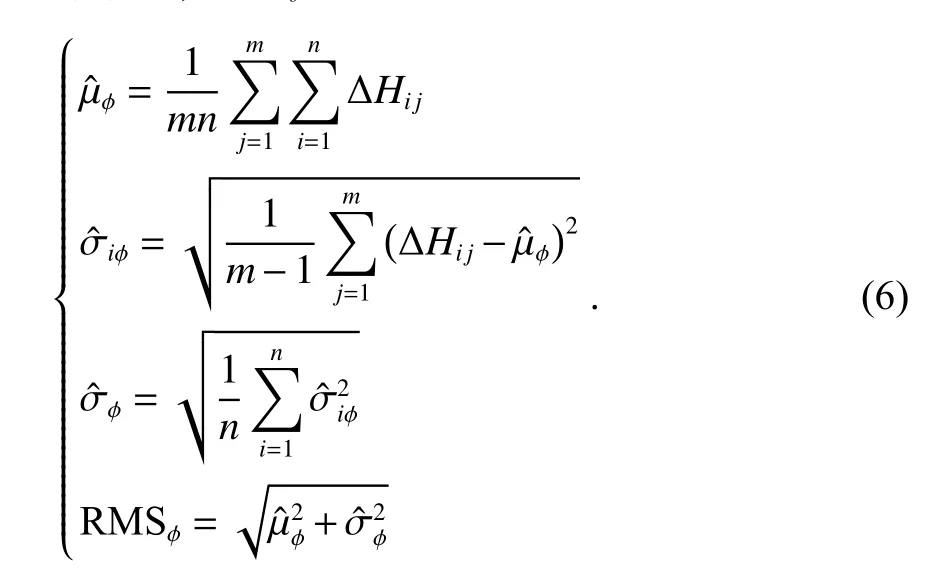
1.3 不确定度分析算法

在GNSS/INS组合导航系统姿态性能测试评估的过程中，容易受到外界各种不确定因素的影响，如测试过程中温度的变化对三轴转台光电编码器、圆光栅等精密器件的精度造成影响，外部不明物理振动冲击以及系统电气噪声等因素也会造成测试基准产生各种误差.

设计的仿真轨迹的偏差，并进行标准差统计作为测试评估过程中转台参考基准的不确定度量值. 转台参考基准不确定度评定公式为

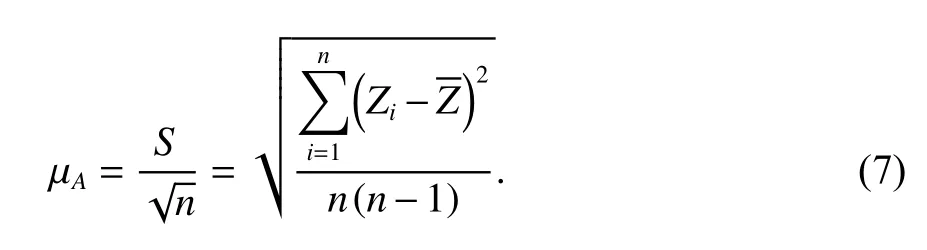
式中：S为标准差；n为采样数；Z为偏差均值；Zi为第i采样点的偏差值.

2 测试评估软件

结合本文所测试的评估算法，图1为测试评估软件，图1中左侧栏为操作控制区，中间栏为视图区，右侧栏为姿态误差曲线实时绘制区.

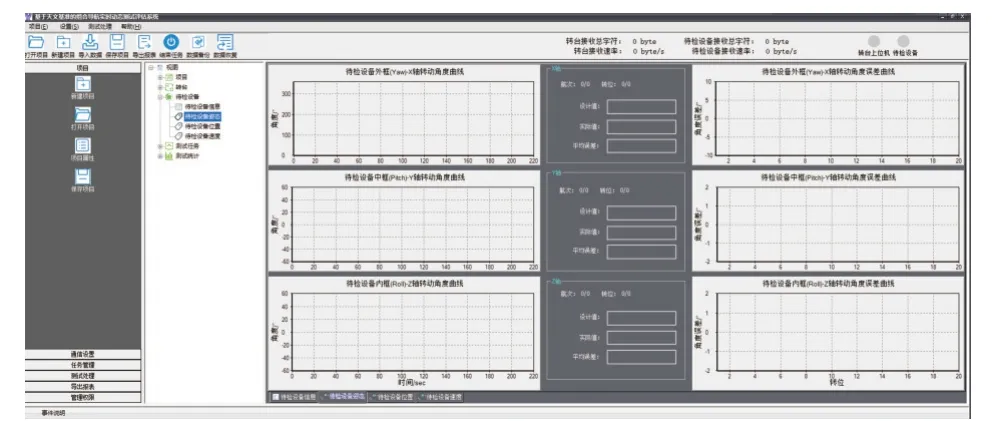
图 1 测试评估软件主界面框架图

2.1 软件运行环境

测试评估软件运行在一个独立的硬件计算机上，分别通过网口、串口与三轴转台、GNSS/INS组合导航设备建立连接，由测试评估软件配置网口和串口通讯参数，实时接收高精度三轴转台和GNSS/INS组合导航设备输出的运动数据，三轴转台的姿态运动数据为基准数据. 接口框图如图2所示.

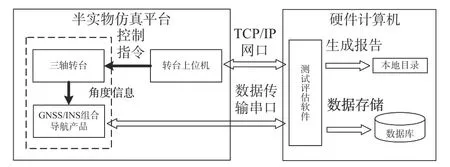
图 2 外部接口框图

2.2 评估任务设计

按照测试评估数据处理流程，本文研究设计了多转位的转向运动测试、俯仰运动测试、横摇运动测试以及复合运动测试任务. 其中，转向运动测试将姿态轨迹设置为转台外框多转位运动模式，中框和内框为固定常值的导航测试，俯仰运动测试、横摇运动测试类似；复合运动测试将转台外、中、内框均设置为多转位复合运动模式的导航测试，实现对GNSS/INS组合导航产品的多姿态综合测试. 通过C++编程语言编译相应的功能函数供用户手动选择，实现测试评估流程的自动化，评估任务设计界面如图3所示.

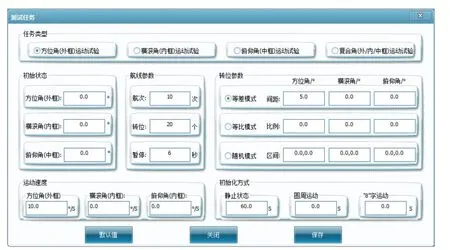
图 3 评估任务设计界面图

3 实测验证与分析

图4为在室外搭建实验平台. 测试所选设备为Newton-M3微机电系统(MEMS)组合导航系统，该产品姿态角技术参数分别为：方位角精度为0.1°；俯仰角精度为0.1°；横滚角精度为0.1°. 设置数据采样频率为10 Hz.

图 4 GNSS/INS组合导航设备实测图

图4中，序号1为GNSS/INS组合导航系统，序号2为天线，序号3为三轴转台.

三轴转台基准参数如表1所示，其中外框轴为方位轴，中框轴为俯仰轴，内框轴为横滚轴. 设置转台数据输出频率为10 Hz.

表 1 三轴转台基准参数

设计两个复合角运动测试评估任务，任务1：共8个航次，每个航次10个转位；任务2：共8个航次，每个航次20个转位. 其中，方位角、俯仰角、横滚角按增量(5°，5°，5°)的方式布设，三框初始位置为(0°，0°，0°). 软件实时误差曲线绘图如图5～6所示. 将实时采集的数据保存至本地后，对各转位上转台实际航行姿态与任务设计的姿态、转台实际航行姿态与组合产品导航解算输出的姿态做差分析，绘图如图7～10所示.

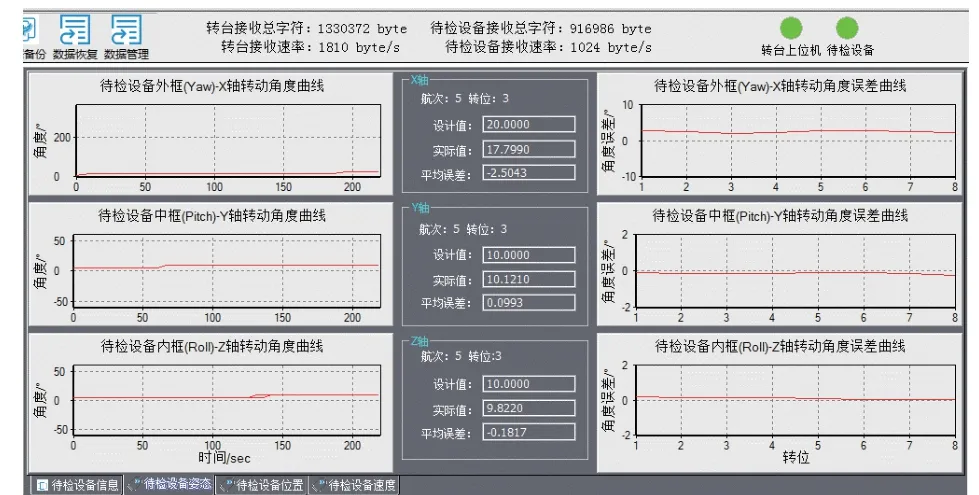
图 5 任务一 实时误差曲线

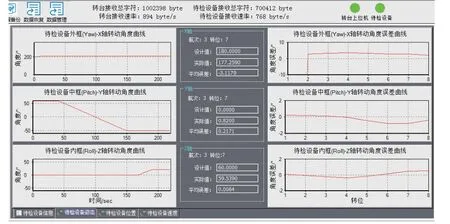
图 6 任务二 实时误差曲线

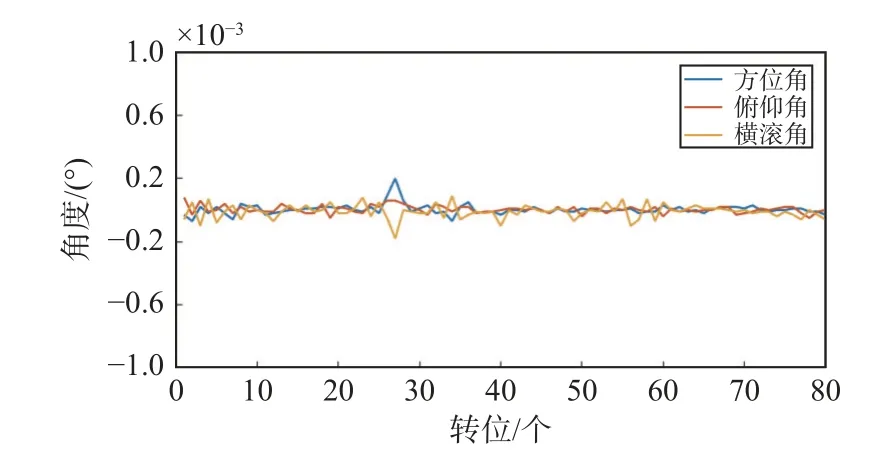
图 7 任务1 转台实际航行姿态误差图

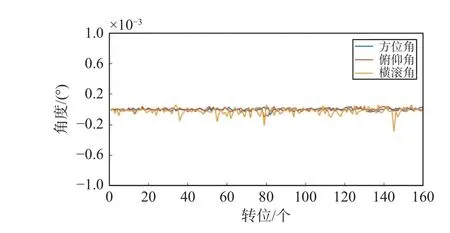
图 8 任务2 转台实际航行姿态误差图

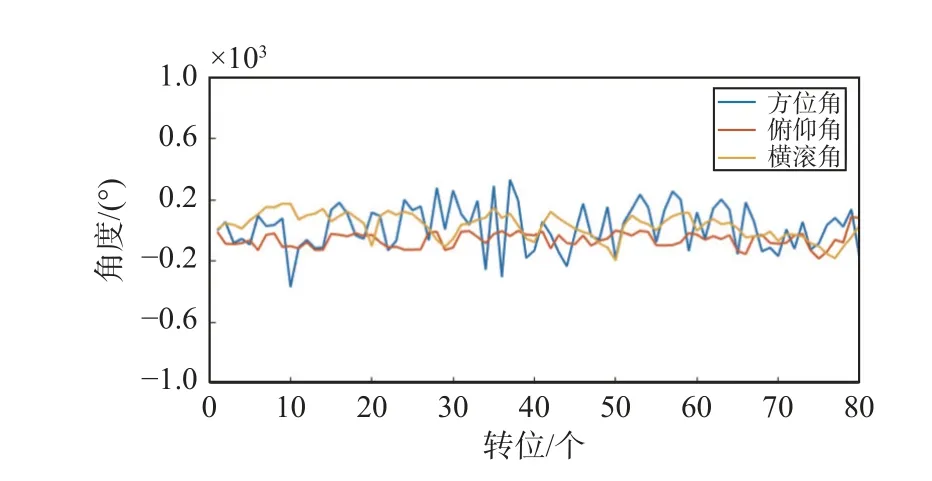
图 9 任务1 Newton-M3航行姿态误差图

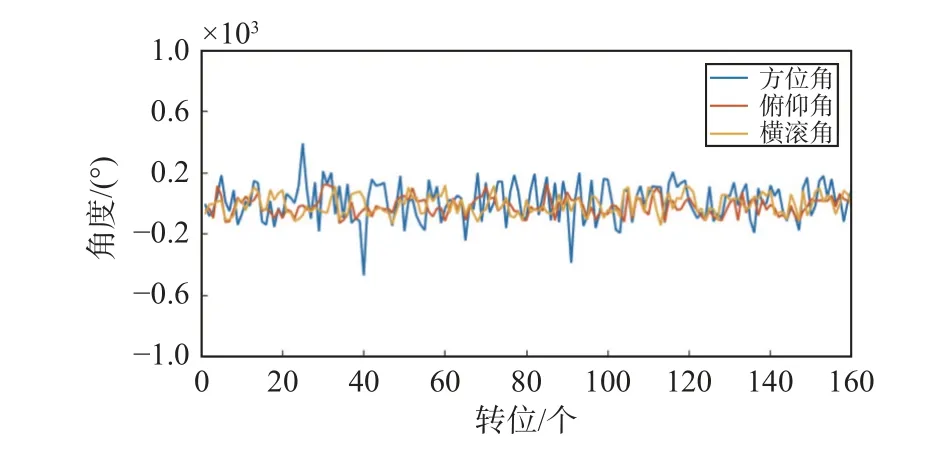
图 10 任务2 Newton-M3航行姿态误差图

由图7～8可知，三轴转台基准方位角、俯仰角和横滚角偏差均在±0.000 25°(0.9″)之内，依次进行不确定度分析，结果如表2所示. 由图9～10可知，Newton-M3组合导航设备方位角、俯仰角和横滚角偏差均在0.6°以内.

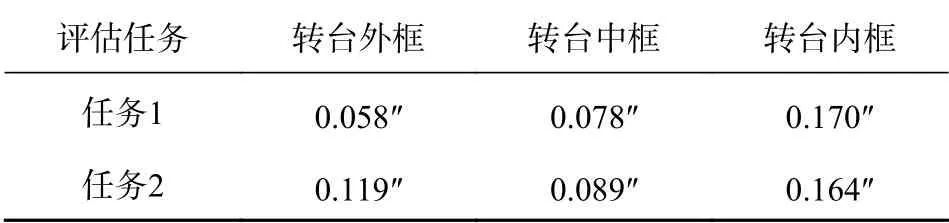
表 2 A类不确定度分析结果

由表2进行分析可知，转台三轴不确定度值均在0.2″以内，表明转台基准数据具有较高地可靠性和可信性.

在转台基准数据中添加一个奇异点，并分两组进行数据处理测试本文提出的方法抑制奇异值的效果，第一组直接进行误差计算和精度统计，第二组通过Thompson奇异值剔除法进行处理后，再进行误差计算和精度统计. 两组测试的姿态误差实时曲线如图11～12所示，表3为最终的测试评估结果.

表 3 Newton-M3测试评估结果

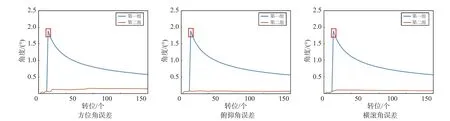
图 11 任务1 Newton-M3姿态误差实时评估结果图

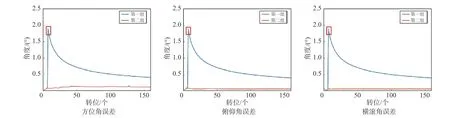
图 12 任务2 Newton-M3姿态误差实时评估结果图

图11～12为两种测试任务下Newton-M3姿态误差实时评估结果图，图中蓝线表示在存在奇异值的情况下直接对测试数据进行误差计算和精度统计的结果；红线表示在经过Thompson奇异值剔除法进行处理后，然后进行误差计算和精度统计的结果，图中红框处为奇异值点所在转位. 由图可知：经过Thompson奇异值剔除法处理之后，能明显改善最终测试评估的结果，姿态误差均更小、精度更优，具有较高的可信性.

对表3进行分析可知，在设计的两个不同的测试任务中，Newton-M3的俯仰角、横滚角精度与自身标称精度指标吻合. 而由于Newton-M3为MEMS组合导航产品，本身难以长时间准确的对方位角进行估计，导致方位角精度要略差于设备的标称精度，但也处于正常范围内. 两组试验中进行Thompson奇异值剔除法处理后的方位角、俯仰角和横滚角RMS误差比未进行处理的结果分别提高了69.87%、84.25%、83.79%和74.22%、86.17%、84.45%.

4 结束语

本文基于高精度三轴转台研究了一种GNSS/INS组合导航系统动态性能测试评估新方法，并研发了相应的测试评估软件进行实现. 本文采用多转位多姿态且具有重复一致性的测试流程对组合导航系统姿态性能进行针对性评估，对采集到转台输出的姿态数据先通过Thompson奇异值剔除法进行处理，保证转台基准数据的可信性，随后将其与组合产品导航解算输出的姿态值作差，并进行RMS误差统计，同时对转台参考基准不确定度进行评价分析，提高测试评价结果的可靠性. 本文对Newton-M3 MEMS组合导航系统进行了两组测试，结果表明：在两种不同测试任务中，所研究方法在存在奇异值点情况下，将组合导航系统方位角、俯仰角、横滚角精度提升69.87%、84.25%、83.79%和74.22%、86.17%、84.45%. 同时转台的不确定度值均在0.2″以内，表明了该测试评估方法具有较高的可行性和可靠性，可为GNSS/INS组合导航产品的开发、定型、生产及验收等方面提供测试评估服务.