基于Park-Ang 损伤模型的网壳结构地震作用下双参数准则研究
2022-09-03叶继红
华 文,叶继红
(1. 江苏省土木工程环境灾变与结构可靠性重点实验室(中国矿业大学),江苏,徐州 221116;2. 徐州市工程结构火灾安全重点实验室(中国矿业大学),江苏,徐州 221116 )
自20 世纪90 年代以来,基于性能的抗震设计方法已成为世界地震工程发展的趋势,它要求将结构划分为多个性能状态[1-4],并强调在不同水平的地震动强度下,能够有效控制结构的损伤概率。网壳结构造型优美、质量轻、刚度强,近年来在城市地标性建筑中得到广泛应用。然而,作为地震发生时的紧急避难场所,网壳结构的破坏或倒塌将带来严重的人员伤亡和经济损失。因此,有必要对网壳结构进行基于性能的抗震设计,合理划分性能状态并建立性能指标。
国外规范SEAOC Vision 2000[5]、ATC-40[6]和FEMA 273[7]已提出多级的性能状态。2004 年,我国颁布的《建筑工程抗震性态设计通则(试用)》[8]体现了基于性能的抗震设计理念,并将结构划分为五种性能状态。我国《建筑抗震设计规范》(GB 50011-2010)[9]在建筑抗震性能设计部分通过位移角限值将结构划分为五种性能状态:基本完好、轻微破坏、中等破坏、严重破坏和倒塌。定义结构的性能状态不仅是基于性能抗震设计方法的重点内容,也是建立易损性曲线、进行地震风险评估的关键步骤。
目前,基于性能的抗震设计理念以及性能状态的划分已应用到许多不同的结构体系[10-25],且大多以强度、变形、能量或变形与能量双控指标作为划分结构性能状态的依据。然而,网壳是由众多杆件组成的空间结构,因其特殊的结构形式,单一参数的指标无法较好地刻画其在地震作用下的损伤情况,而变形与能量双控指标有着考虑因素更全面、合理等优势。1985 年,Park 和Ang[26]根据大量钢筋混凝土柱构件试验结果,提出适用于钢筋混凝土构件在地震作用下的损伤模型,该模型采用规格化最大位移和规格化滞回耗能的线性组合方式。此后,较多学者对其进行修正并应用在其它构件和结构中。Chai 等[27]考虑到单调加载至破坏时结构将耗散一定能量,对Park-Ang 损伤模型进行修正。江近仁和孙景江[28]根据45 个砖墙重复循环加载恢复力曲线,得到适用于砖结构的地震双参数模型。针对钢结构和钢筋混凝土结构,欧进萍等[29]和牛荻涛等[30]提出了位移项与耗能项采用非线性组合形式的双参数改进模型。周知等[31-32]对模型进行修正,解决Park-Ang 损伤模型上、下界不收敛问题并应用于钢构件和剪力墙构件中。门进杰等[33]与尚庆学等[34]通过修正Park-Ang 双参数模型分别得到适用于RCS混合框架结构和RC 剪力墙结构的损伤模型。杜文风等[35]考虑单层球面网壳结构的变形和耗能,以Park-Ang 损伤模型为原型用于单层球面网壳结构,并将位移与耗能对损伤的贡献按1∶1 比例体现,但该准则存在参数物理意义不明确的问题,且缺少试验验证。
鉴于此,本文以经典Park-Ang 损伤模型为基础,综合考虑位移与耗能对网壳损伤的贡献,建立由最大变形与塑性耗能两项无量纲参数非线性组合的双参数模型;根据我国《建筑抗震设计规范》[9]、网壳结构在地震作用下的破坏情况与以往学者的研究成果,以地震作用下最大位移响应δM、开始进入塑性时最大位移响应δP与塑性杆件比例P作为判断依据,通过性能点LS-1、LS-2、LS-3 与LS-4 将网壳结构的性能状态划分为基本完好、轻微破坏、中等破坏、严重破坏和倒塌五种状态;根据考虑不同跨度、矢跨比、屋面质量、杆件尺寸与地震作用的216 组数值模拟算例计算结果,拟合得到模型中待定参数α、β 和γ 的取值,并提出适用于网壳结构的双参数准则及划分指标。最后,以叶继红教授课题组[36]的两个K6 型单层球面网壳结构振动台试验为例,验证双参数准则的普适性。
1 网壳结构双参数模型
Park 和Ang[26]在1985 年根据一批钢筋混凝土柱构件试验结果,提出适用于钢筋混凝土构件在地震作用下的损伤模型:

此外,模型假定最大变形和累积滞回耗能对损伤的贡献为线性关系,而网壳结构的位移与耗能对损伤的贡献并非为线性关系。以跨度为40 m的K8,6型单层球面网壳结构为例(如图1 所示),观察网壳结构的位移与耗能随地震动发展的响应情况。结构矢跨比为1/3,结构周边为三向固定铰支座,环向杆件采用95 mm×3.5 mm,斜向及径向杆件采用102 mm×3.5 mm,结构材料选用Q235钢,弹性模量2.06×105MPa,采用理想弹塑性模型,考虑结构承受的荷载为60 kg/m2。

图1 K8,6 型单层球面网壳结构Fig. 1 K8,6 single-layer spherical reticulated shell structure
在ANSYS 中对结构进行分析,杆件采用PIPE20 单元模拟。对结构进行静力弹塑性全过程

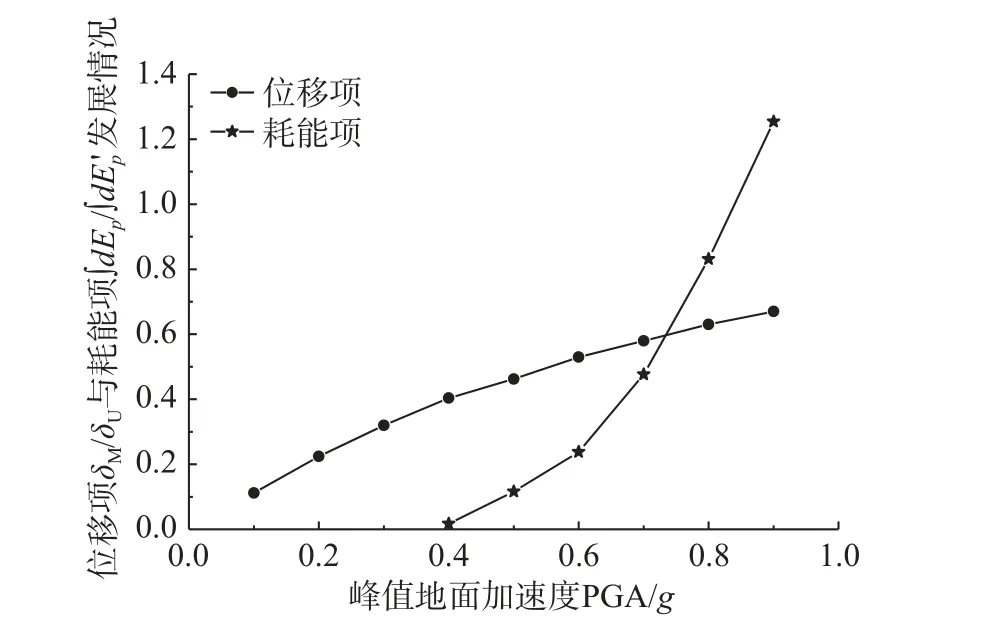
图2 网壳结构位移项与耗能项随地震动强度发展情况Fig. 2 The development of displacement term and energy dissipation term of the reticulated shell structure with the intensity of ground motion
由此,在Park-Ang 损伤模型的基础上,结合网壳结构位移与耗能在地震下的响应特点,并考虑模型的普适性,引入α、β 和γ 待定参数,将位移项与耗能项作为非线性组合的形式,提出适用于网壳结构的双参数模型:


2 网壳结构性能状态的定义及划分
基于性能的抗震设计要求将结构划分为多个性能状态。不同于以层间位移等单一参数可衡量结构在地震作用下发展情况的多高层建筑,网壳为高次超静定结构,其失效形式不但包括以位移发散为判定依据的动力失稳,还可能发生由于塑性变形过度发展而导致的强度破坏[37-38],故需从位移与塑性发展两方面共同衡量网壳结构在地震作用下的响应情况,常见的参数有最大节点位移、塑性杆件比例、杆件应变、结构应变能等[35,37-40]。
结合《建筑抗震设计规范》[9]、网壳结构的自身动力特性与前人的研究成果[35,37-40],以地震作用下最大位移响应δM、开始进入塑性时最大位移响应δP与塑性杆件比例P作为划分依据,将网壳结构的性能状态划分为基本完好、轻微破坏、中等破坏、严重破坏和倒塌这五种状态,其各性能状态下对应的结构响应情况、震后措施与划分依据列于表1 中。当结构开始出现塑性杆件之前,认为结构处于基本完好状态,根据P=0 即可判断,且此时最大节点位移δM<δP;当位移发散时,认为结构倒塌,根据δM=∞即可判断。考虑到网壳的失效形式为动力失稳与强度破坏且大多数两者兼具,当以动力失稳为主要破坏形式时,位移响应较明显而塑性发展不大;当以强度破坏为主要形式时,塑性发展相对前者较明显。为使所得准则具有普适性,轻微破坏、中等破坏和严重破坏这三种破坏等级需从位移与塑性发展两方面判断。当结构的位移与塑性发展分别满足两种破坏状态时,取最不利情况。

表1 网壳结构性能状态与划分界限[9,35,37-40]Table 1 Performance levels and descriptions of reticulated shell structures[9,35,37-40]
划分五种性能状态的四个性能点分别为LS-1、LS-2、LS-3 与LS-4,各性能点处的判断依据如表2所示。性能点LS-1 为结构处于弹性与塑性的临界状态,当结构开始出现P>0 时即可判断,并将此时的最大节点位移记为δP;性能点LS-4 为结构倒塌的临界状态,当结构开始出现最大节点位移δM发散时即可判断。在性能点LS-2 与LS-3 处,从位移和塑性发展两方面判断,即当结构处于最大节点位移δM≥2.5δP或塑性杆件比例P>15%的临界状态为性能点LS-2 的判断依据,当结构处于最大节点位移δM≥10δP或塑性杆件比例P>45%的临界状态为性能点LS-3 的判断依据。

表2 各级性能点判断依据Table 2 Judgment criterion for performance points at all levels
3 网壳结构数值计算模型
为得到式(2)待定参数α、β 和γ 的取值,并找到划分每个性能点的D值,通过数值模拟算例对网壳结构在各级性能点处的位移与耗能进行统计分析。其中,在LS-4 处计算得到的D值均为无穷,故不作统计。
根据《空间网格结构技术规程》[41]的要求,建立考虑不同跨度(40 m、50 m、60 m)、矢跨比(1/3、1/5、1/7)、屋面质量(60 kg/m2、120 kg/m2、180 kg/m2)的K6、K8 型单层球面网壳结构模型算例,为保证所得准则具有普适性,所有参数均在工程常用范围内选取,具体模型参数详见表3。结构周边为三向固定铰支座,材料选用Q235 钢,屈服强度235 MPa,弹性模量2.06×105MPa,Reyleigh阻尼,阻尼比为0.02,采用理想弹塑性本构模型。每种网壳采用两种尺寸的杆件,环杆和斜杆采用较小尺寸,径杆采用较大尺寸。所选网壳算例均已进行静力稳定性计算,各算例的稳定安全系数K在2.00~5.88 范围内,同时杆件受力强度与结构挠度也满足规范[41]要求。在ANSYS 中对模型进行数值模拟计算,杆件采用BEAM188 单元模拟,每根杆件划分为三个单元;在动力分析时荷载采用质量块单元MASS21 模拟。从ATC-63[42]选 取Northridge-01、Imperial Valley-06、Duzce、Hector Mine 四种不同波形的地震波,采用增量动力分析(Incremental Dynamic Analysis,IDA)方法分别输入到结构中。为提高计算效率,选用90%能量持时[43]。共计216 组算例,每组统计3 个性能点处(表2 中LS-1、LS-2 与LS-3)的位移与耗能情况。

表3 K6、K8 型单层球面网壳结构数值计算模型参数Table 3 Numerical calculation model parameters of K6, K8 single-layer spherical shell structures
4 双参数准则的拟合
为让各级性能点所得D值更加简明,首先,令性能点LS-3 处的D=1,按照式(2)对LS-3 处的216 组算例结果进行回归拟合,得到α=0.2,β=0.4,γ=0.1,如式(3):
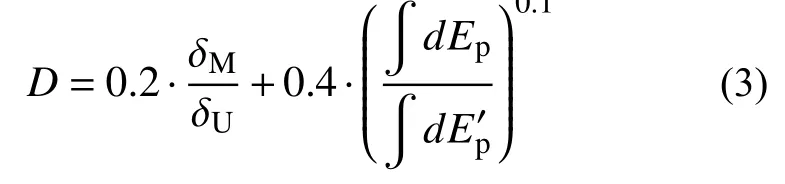
然后,将216 组算例在LS-1 与LS-2 处的计算结果代入式(3),得到的D值如图3 所示,其中,性能点LS-1 与LS-2 处算例结果的均值分别为0.3 与0.6,方差均为0.002,拟合精度良好。因此,式(3)可作为适用于网壳结构的双参数准则。此外,由图3 可知,该三组数据点均趋近于均值,故取0.3、0.6 与1 作为各级性能点的划分指标,具体详见表4。

表4 网壳结构双参数准则性能状态划分Table 4 Performance level divisions of the two-parameter criterion for reticulated shell structures

图3 相应于各级性能点的D 值计算结果Fig. 3 Calculation results of D values corresponding to performance points at all levels
5 大型振动台试验验证双参数准则
5.1 模型概况
以叶继红教授课题组[36]的大型网壳振动台试验为例验证双参数准则的普适性。2 个K6 型单层球面网壳试验模型的原型跨度均为81.9 m,矢跨比为1/2,试验缩尺比1∶3.5,缩尺后跨度为23.4 m。每个模型节点总数为1261,杆件总数为3660。模型1 整体刚度均匀;模型2 在模型1 的基础上设置了两个薄弱区,并增大顶部杆件截面,使两模型用钢量相同,方便对比与模型1 倒塌过程的差异。结构模型如图4 所示,模型2 的薄弱区分布详见图5。试验利用同济大学多点振动台试验系统完成,该系统由 A、B、C、D 四个振动台组成,每个振动台上有10 个支座,周边其他节点不设支座。振动台分布与支座情况如图5 与图6 所示。

图4 模型与振动台[36]Fig. 4 Model and shaking tables[36]

图5 模型2 薄弱区与振动台编号[36]Fig. 5 The weakened zones of model 2 and shaking table number[36]

图6 模型支座约束[36]Fig. 6 Model support constraints[36]
5.2 试验加载
分别在四个振动台处沿Y向(如图5 所示)输入一条EL-Centro 地震波,地震波满足设定的自谱与互谱关系。考虑相似关系后,地震波持时28.58506 s,时间间隔0.01069 s,各个振动台输入的地震波时程如图7 所示。采用IDA 方法,逐级提高PGA,分别观察并记录两个模型的倒塌破坏过程。
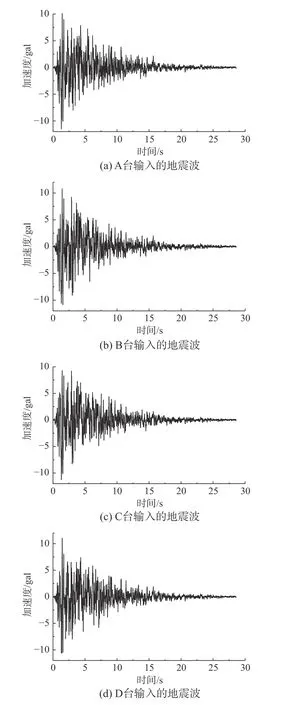
图7 地震波时程曲线[36]Fig. 7 Seismic wave time history curves[36]
5.3 双参数准则的验证



表5 网壳试验模型1 对双参数准则的验证Table 5 Validation of the two-parameter criterion by the reticulated shell test model 1

表6 网壳试验模型2 对双参数准则的验证Table 6 Validation of the two-parameter criterion by the reticulated shell test model 2
对于试验模型1(正常设计的模型):在PGA为100 gal 时,结构振动幅度微弱,仿真得到最大节点位移δM为4.8 mm,无杆件进入塑性,依据表1 的划分依据,此时结构处于基本完好状态,将仿真结果代入式(3),计算得到D值为0.02,通过与表4 对比可知,该D值在基本完好状态的划分范围0~0.3 内;在PGA 为200 gal 时,C、D 台面之间的结构下部首次出现少量弯曲杆件(如图8(b)),此时仿真得到最大节点位移δM为9.6 mm,在C、D 台面之间结构下部开始有杆件进入塑性,塑性杆件比例P为0.74%,依据表1 可知,结构处于轻微破坏状态,计算得到D值为0.38,对比表4可知,该D值符合轻微破坏状态的划分范围0.3~0.6;在PGA 达到250 gal 时,位移进一步发展,仿真得到最大节点位移δM为20.3 mm,约为跨度的1/1150,塑性杆件比例P为1.52%,由表1可知结构仍处于轻微破坏状态,计算得到D值为0.43 且在表4 的划分范围0.3~0.6 内;在PGA 为300 gal~350 gal 过程中,C、D 台面之间的结构下部斜向杆件逐渐弯曲,范围有明显的发展扩大过程(如图8(c)),此时仿真得到最大节点位移δM分别为44 mm 与71 mm,约为跨度的1/530 与1/325,塑性杆件比例P分别达到2.1%与3.9%且集中于C、D 台面之间,由表1 可知,虽然塑性发展仍处于轻微破坏但位移已达到中等破坏状态,依据“当结构的位移与塑性发展分别满足两种破坏状态时,取最不利情况”的原则,在300 gal 与350 gal下结构均为中等破坏状态,相应计算得到的D值分别为0.61 与0.72,均在表4 的划分范围0.6~1.0 内;当PGA 为400 gal 时,上述损伤区域进一步迅速扩大,结构在短时间内整体向下坍塌(如图8(d)),此时仿真得到的最大节点位移δM发散,由表1 知结构处于倒塌状态,计算的D值为∞,满足表4的划分。

图8 模型1 试验过程[36]Fig. 8 Test process of model 1[36]
对于试验模型2(薄弱模型):在PGA 为100 gal时,结构振动平稳,仿真得到最大节点位移δM为7.3 mm,未有杆件进入塑性,由表1 可知结构为基本完好状态,由公式(3)计算得到D值为0.03且满足表4 的划分(0~0.3);在PGA 为200 gal时,结构振动加剧,但变形不明显,此时仿真得到最大节点位移δM为15 mm,塑性杆件比例P为0.49%,依据表1 可知,结构开始有杆件进入塑性,处于轻微破坏状态,计算的D值为0.34,在表4 的划分范围0.3~0.6 内;在PGA 为250 gal时,结构中薄弱区突然发生凹陷,其它部分仍无明显变形(如图9(b)),此仿真得到时最大节点位移δM为72 mm,约为跨度的1/325,有5.9%的杆件进入塑性且集中于薄弱区的凹陷部位,由表1可知,塑性发展仍为轻微破坏状态,而位移进入中等破坏状态,依据“最不利原则”,此时结构为中等破坏状态,计算得到D值为0.71 且在0.6~1.0 范围内(表4);加载至300 gal,结构凹陷部分位移明显增加,凹陷区逐渐扩大,但结构其它部分仍无明显变形(如图9(c)),此时最大节点位移δM为150 mm,已达到跨度的1/156,有7%杆件进入塑性,依据表1 可知,虽塑性发展仍为轻微破坏状态,但位移已达到严重破坏状态,故此时结构为严重破坏状态,计算的D值为1.03,在表4 划分的严重破坏状态范围内(≥1.0);在PGA为350 gal 时,结构突然发生倒塌(如图9(d)),仿真得到的最大节点位移δM发散,由表1 知此时为倒塌状态,相应的D值为∞,满足表4 的划分。

图9 模型2 试验过程[36]Fig. 9 Test process of model 2[36]
由此可知,两个模型在每种工况下依据双参数准则计算得到的D值均在各性能状态所对应指标的范围内,且四个性能点的指标值(0.3、0.6、1 和∞)能较好地划分网壳结构的5 个性能状态,由此验证了准则的有效性和普适性。
6 结论
本文将基于性能的抗震设计理念引入网壳结构,基于Park-Ang 损伤模型提出适用于网壳结构的双参数模型,并通过四个性能点将网壳结构划分为五种性能状态;在此基础上,根据216 组覆盖性网壳实例(考虑不同跨度、矢跨比、屋面质量、杆件尺寸与地震作用)拟合得到适用于网壳结构的双参数准则;最后通过两个大型网壳振动台试验模型对准则的有效性和普适性进行验证。得到以下结论:
(1)结合我国规范、网壳结构自身动力特性与前人的研究成果,以地震作用下最大位移响应δM、开始进入塑性时最大位移响应δP与塑性杆件比例P作为判断依据,将网壳结构的性能状态划分为基本完好、轻微破坏、中等破坏、严重破坏与倒塌五种状态。
(2)考虑网壳结构在地震下的响应特点,基于Park-Ang 损伤模型提出适用于网壳结构的双参数模型,该模型以位移和耗能作为非线性组合的形式呈现且物理意义明确,能综合考虑位移与耗能对网壳损伤的贡献,基本涵盖网壳结构在地震作用下的失效形式。根据216 组覆盖性网壳结构算例拟合,得到对应于上述五种状态的性能点LS-1、LS-2、LS-3、LS-4 处 的 指 标 值D分 别 为0.3、0.6、1.0 与∞。该准则经2 个大型K6 型单层球壳结构振动台试验验证,能较好地划分网壳结构的各个性能状态,具有良好的有效性和普适性。
(3)通过双参数准则,研究者可以定量得知网壳结构在地震作用下的损伤情况与破坏等级,进而为结构震后加固与维修、人员伤亡与经济损失的统计提供依据,为网壳结构基于性能的抗震设计与地震风险评估奠定了基础。
