基于概率的高层建筑地震需求模型与风险评估

郑晓伟，李宏男，张营营，尹世平

(1. 中国矿业大学力学与土木工程学院，江苏，徐州 221116；2. 大连理工大学建设工程学部，辽宁，大连 116024；3. 沈阳建筑大学土木工程学院，辽宁，沈阳 110168)

城市区域的人口快速增长和经济高速发展，促使高层建筑等高性能结构建设越来受到工程界的重视，仅2020 年，全球范围内共完成106 栋200 m 以上的建筑，其中57 栋在中国，占总数的53%[1]。目前关于高层建筑的抗震研究主要集中在结构整体/局部承载能力[2]、构件强度[3]和耗能减震[4]等方面，缺少基于概率的高层建筑地震风险评估研究[5]。工程结构在地震作用下的破坏风险概率定义为：结构响应达到或超过某一极限状态时的可能性[1]，主要包含2 部分内容：① 地震事件的危险性分析；② 结构的易损性分析。

地震危险性分析，即确定所研究地区在结构服役期内可能发生不同强度地震的概率，是开展工程结构地震风险评估的首要任务。目前针对地震概率模型的研究相对成熟，Cornell[6]首次提出了基于概率的地震危险性分析方法，并建议以平稳泊松分布描述地震事件。我国是世界上地震频发地区之一，高小旺等[7]对华北、西北和西南3 个地区45 个城镇的地震危险性进行了统计分析，指出地震动峰值加速度(peak ground acceleration, PGA)的概率分布符合极值II 型分布。美国地质调查局USGS(U.S. Geological Survey)依托其丰富的实测地震数据，给出了美国境内的地震危险性曲线，并提供了查询不同超越概率危险性的工具，这为基于风险一致性设计准则的发展提供了条件[8]。我国抗震设计规范[9]给出了主要城镇小震、中震和大震对应的PGA 取值，据此可反算出上述3 类强度地震所对应的年超越概率，通过插值法也可进一步获得关于PGA 的地震危险性曲线，但由此确定的危险性模型离散性较大。鉴于此，郑晓伟等[1,5,10]和李宏男等[11]，以中国地震局强震台网中心提供的1970 年～2017 年间仪器地震记录和地震目录为研究基础，对云南大理地区开展了基于概率的地震危险性分析，并给出了关于PGA的危险性曲线。另外，为考虑地震危险性分析中的不确定性，贝叶斯更新技术开始应用于该领域，例如地震波形反演[12]、地震震级预估[13]和地震危险性分析[14]。

结构易损性作为连接灾害概率模型和结构破坏风险之间的纽带，其定义为：在极端事件发生的条件下，工程需求参数(engineering demand parameter, EDP)达到特定极限状态的条件概率[15]。研究人员对地震作用下高层建筑的易损性开展了系列研究[16-18]，且常选取最大层间侧移[19]、顶层最大位移[5]等指标来衡量结构的性能水平。另外，李宏男等[20]对地震易损性的发展历程和研究现状进行了系统梳理，分别对经验分析法、数值分析法和混合方法的优缺点以及计算要点进行了总结，并进一步强调了随机变量不确定性对易损性分析的重要意义。Ang 和Tang[21]指出，不确定性可分为两大类：固有不确定性(aleatory uncertainty)和认知不确定性(epistemic uncertainty)。目前，随机抽样方法常被用来考虑与材料力学特性相关的认知不确定性[22]；而通过选取大量地震动记录的方法来考虑输入地震荷载的固有不确定性[23]，且通常认为输入荷载的不确定性在易损性分析中起主导作用[24]。而大量研究表明[25-27]，易损性分析中结构参数不确定性与地震动记录不确定性的影响程度相当。需要指出的是，计算结构易损性时通常假定结构的需求和能力服从正态分布或对数正态分布。但由此仅能得到结构易损性的点估计值，却无法反映结构能力模型(C)和工程需求模型(EDP)中参数不确定性的影响。鉴于此，Gardoni等[28-29]通过贝叶斯理论，发展了基于概率的结构能力和工程需求模型，而结构易损性可由严格可靠度分析确定。

本文将针对高层建筑开展基于概率的地震需求模型和易损性研究，并提出基于概率的高层建筑地震风险分析方法。以中国地震局强震台网中心提供的地震数据为研究基础，首先开展基于贝叶斯理论的地震危险性分析，建立具有更新功能的地震概率模型。其次，通过贝叶斯理论建立地震需求模型，以此考虑需求模型不确定性对结构易损性的影响。最后，以某42 层钢框架-RC 核心筒建筑为研究对象，展示基于概率的风险评估方法。本文的研究成果有助于提高工程界对工程结构地震风险的认识，且可为规程中相关条文的修订提供科学依据。

1 基于贝叶斯理论的地震风险评估

地震作用下高层建筑结构响应达到不同极限状态的破坏风险概率λR，可表示为地震发生频率与结构易损性乘积的积分，即：

本文将采用马尔科夫链-蒙特卡罗(Markov chain-Monte Carlo, MCMC)抽样方法[32]，确定模型中未知参数的后验估计值。在执行MCMC 算法时，需采用足够的分析步数来保证所有未知模型参数均满足收敛性要求。

2 数据来源及分析

云南大理地处云贵高原的中-甸地震带上，地质构造复杂，是我国地震活动最为频繁的地区之一。大理地区现布置有强震台站27 座，选取该地区2007 年-2017 年间的仪器实测PGA 记录，实测地震动记录的震中距和震级分布图绘于图1。由于我国强震台站布置周期较短，实测数据不足以进行该地区的地震危险性分析，因此借助1970 年-2017 年间的地震目录，通过地震动衰减模型补充PGA 数据，并将其定义为半实测PGA 记录[1]。

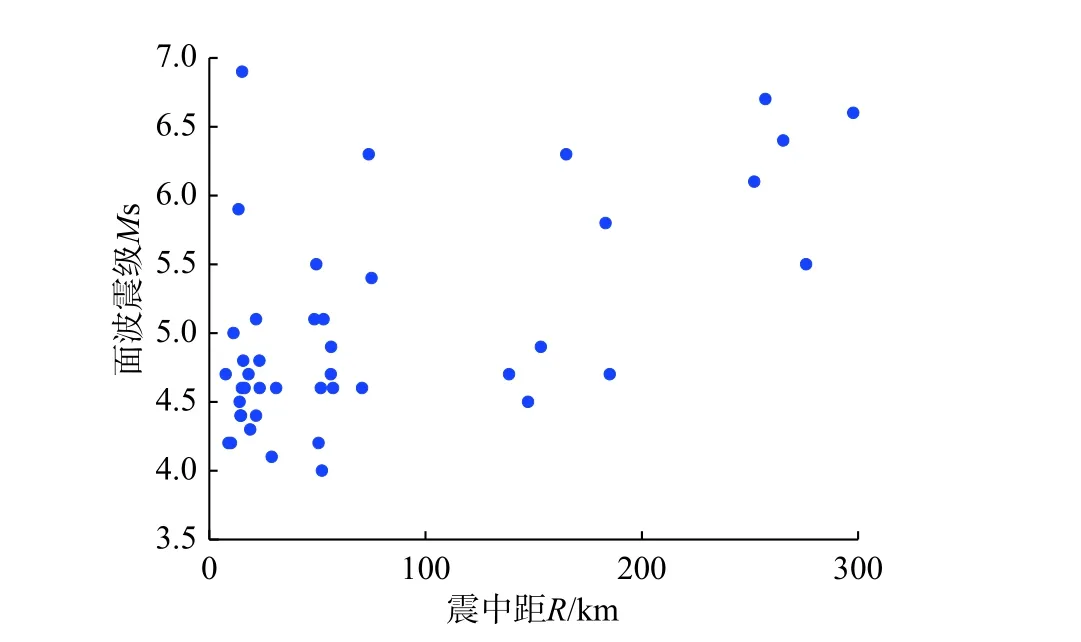
图1 震中距-震级分布图Fig. 1 The distribution of epicentral distance-magnitude

为考虑衰减模型不确定性对地震危险性分析的影响，本节选取Benchmark 模型(Model I)[33]和我国规范中采用的模型(Model II)[1]。基于实测PGA 数据，通过回归分析的方法确定衰减模型中参数c1～c6的取值，Model I：c1=0.164、c2=0.896和c3=-1.980；Model II：c1=-0.119、c2=0.045、c3=0.067、c4=-1.463、c5=52.32 和c6=-0.453。

Model I: lnPGA=c1+c2m+c3ln(R+25) (6)

在实测地震数据和地震目录中选取面波震级Ms≥4 和震中距R≤300 km 的地震数据，共获得683 个PGA 数据样本。该数据集包含2 类样本：样本I 由实测PGA 数据和由Model I 得到的半实测PGA 数据构成；样本II 包括实测PGA 数据和由Model II 得到的半实测PGA 数据。

3 基于贝叶斯理论的地震危险性分析

本节在概率地震危险性分析方法(probabilistic seismic hazard analysis, PSHA)的基础上，给出了基于贝叶斯理论的地震危险性分析方法(Bayesianbased PSHA, B-PSHA)，由该方法确定PGA 大于给定值x的年平均超越概率为：

式中，Rt为震中距R的限值，取300 km[10-11]。

本节选取对数正态分布描述PGA 的概率分布[34]，基于贝叶斯理论确定模型中未知参数的后验概率分布。对不同数据样本，模型中未知参数的后验估计值汇总于表1，其中，m=1，2。

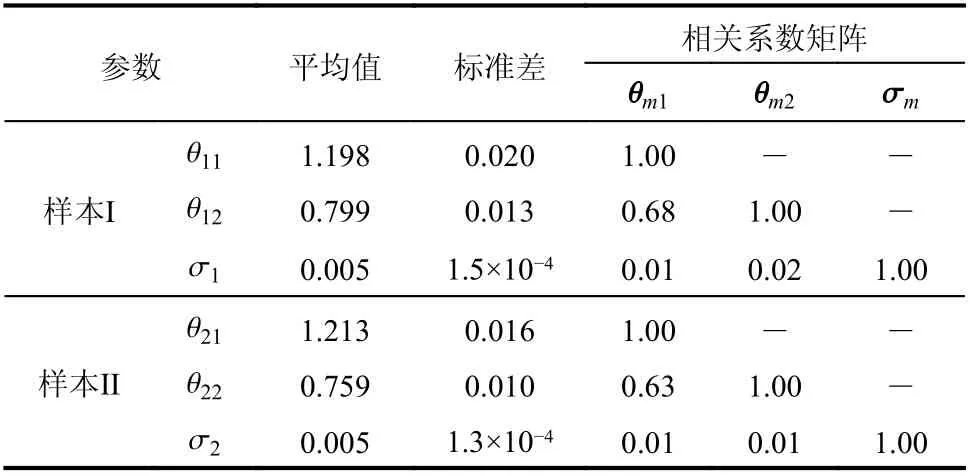
表1 PGA 概率模型未知参数的后验估计值Table 1 Posterior statistics of unknown parameters in the probability distribution of PGA

除PGA 概率模型不确定性的影响外，本文另通过逻辑树方法考虑古登堡-里克特系数b、最大震级和地震动衰减模型不确定性对B-PSHA 结果的影响。其中，逻辑树中系数b分别取0.70、0.74和0.79，其权重可由文献[37]确定，分别为0.125、0.75 和0.125；最大震级分别取7.0、7.5和8.0，其相应权重可由地震目录计算确定，分别为10/19、7/19 和2/19；两类衰减模型的权重均为0.5。图2中给出了由传统PSHA 方法(虚线)和B-PSHA 方法(实线)确定的地震危险性曲线。从图可见，由B-PSHA 方法得到的危险性曲线衰减速度慢于传统PSHA 方法的结果，且B-PSHA 方法得到的危险性曲线更符合实际情况。

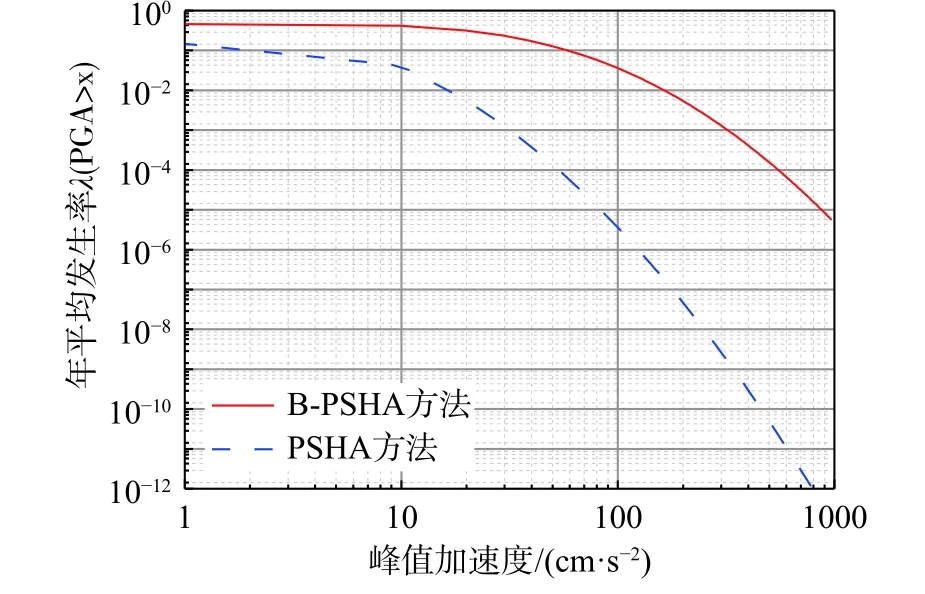
图2 关于峰值加速度的地震危险性曲线Fig. 2 Seismic hazard curve of PGA

4 基于贝叶斯理论的地震易损性分析

地震易损性定义为在给定PGA 条件下，结构响应达到给定极限状态的条件概率[1,38]。其中，极限状态方程写作[28]：

为探究基于概率的地震风险评估方法，按现行规范[9,40]设计了一个42 层钢框架-RC 核心筒建筑，其长度和宽度分别为32.4 m 和30.6 m，平面布置图见图3(a)。该高层建筑总高为152.1 m +3.0 m 设备层，其中，第一层高度为4.5 m、其他层高度均为3.6 m。在OpenSEES 平台上对该高层建筑进行动力非线性时程分析，其中，圆钢管柱和I 字型钢梁均采用非线性梁柱单元模拟，RC 剪力墙由分层壳单元模拟，其三维有限元模型如图3(b)所示。有限元模型中，钢材本构模型为Steel02，混凝土本构模型由Concrete02 描述。

图3 高层钢框架-RC 核心筒建筑的布置图Fig. 3 The layout of the high-rise steel frame-RC core tube building

本文除考虑对需求模型认知不确定性的影响外，还通过拉丁超立方抽样方法[41]，随机生成20 个高层建筑的有限元模型样本，以此考虑材料参数和阻尼比不确定性的影响。其中，材料参数和阻尼比的概率分布和变异系数见文献[1]。为考虑输入地震动记录的固有不确定性，本文根据我国抗震规范[9]中8 度(0.2g)设防烈度对应的目标谱，从PEER-NGA 数据库中获取97 条地震动记录。其中，包括30 条普通地震动、30 条远场谐波型地震动和37 条近场脉冲型地震动[42]；另从汶川地震记录中选取3 条远场谐波型地震动，总计100 条地震动记录。所选100 条地震动的响应谱与目标谱绘于图4。

图4 地震动记录响应谱与目标谱对比Fig. 4 Comparison of the response and target spectra

图4 表明，本节所选取的地震动记录符合抗震规范要求[9]，可用于后续非线性动力分析。将100 条地震动记录与20 个有限元模型随机匹配，形成20 组“有限元模型-地震动记录”，即每个模型随机匹配5 条地震动记录。选择最大层间侧移角来衡量结构在地震作用下的性能水平，共选取了六级极限状态，其量化指标如表2 所示。

表2 极限状态及其量化Table 2 Damage levels and limit states

通过OpenSEES 平台对该高层建筑进行地震作用下的非线性动力时程分析，其中，地震作用分别沿高层建筑X和Y轴方向单独加载。根据贝叶斯更新准则确定需求模型中参数的后验概率分布，参数的后验估计值汇总于表3，其中k=X和Y。

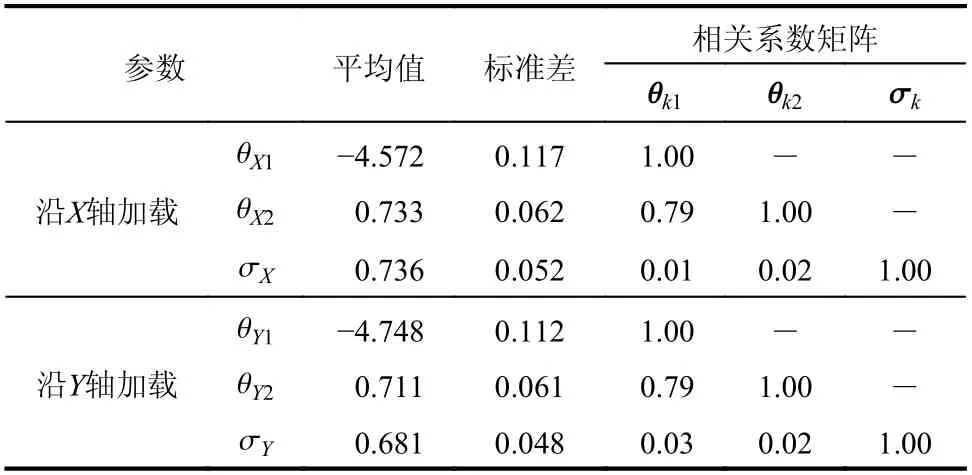
表3 需求模型中参数的后验估计值Table 3 Posterior statistics of the parameters in the demand model

将平均需求模型，即参数取平均值时，绘于图5，其中，虚线对应的置信区间边界为平均值±σX和±σY。从图5 中不难看出，地震作用沿X轴加载时，结构响应在ln(PGA)为[-2, 0]和ln(最大层间侧移角)为[-6, -4]区间内更为集中。这主要是因为，对该高层建筑而言，结构X轴的刚度小于Y轴刚度。

图5 地震需求模型Fig. 5 Seismic demand model

为探讨考虑需求模型中未知参数不确定性与否对易损性的影响，将中度破坏(DS3)和重度破坏(DS4)对应的易损性曲线绘于图6(a)。从图6(a)中相对难以发现易损性之间的差异，因此，为更加具体对比需求模型不确定性对易损性的影响，此处引入差异率=100×(FYE-FNO)/FNO，其中YE和NO 分别表示考虑与不考虑不确定性，计算结果如图6(b)所示。从曲线对比图中可以发现，易损性间最大差异接近15%。另外，当地震动记录沿X轴加载时，不考虑需求模型的不确定性会低估结构地震易损性；相反，当地震作用沿Y轴加载时，不考虑需求模型的不确定性会高估地震易损性。因此，在结构的地震易损性分析中，应充分考虑需求模型不确定性对分析结果的影响。并且，本文并未考虑能力模型(C)不确定性的影响，在今后的研究中应计入能力模型不确定性对结构地震易损性的影响，该差异也许会更加显著。

图6 考虑需求模型不确定性与否的地震易损性Fig. 6 Fragility curves with and without uncertainty in demand models

结构需求模型中未知参数的后验概率分布确定后，根据式(14)计算不同极限状态下的地震易损性。图7 以轻微破坏、中度破坏和严重破坏为例，展示了地震作用分别沿结构X轴和Y轴加载时的易损性曲线。由图7 可知，沿X轴加载的结构易损性大于沿Y轴的值，这主要是因为，与X轴相比，该高层建筑沿Y轴的刚度较大。

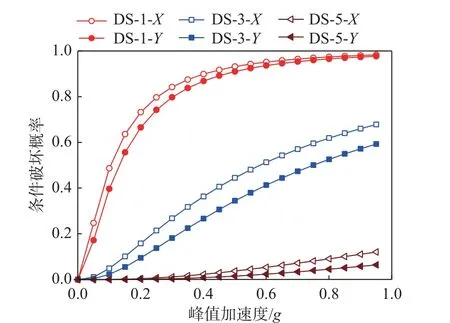
图7 地震易损性曲线Fig. 7 Seismic fragility curves

5 高层建筑的地震风险评估

本文以PGA 作为地震作用的强度指标，结构响应达到给定极限状态的年平均发生率，即式(1)可写作：

需要指出的是，式(15)积分号内的部分可看作累积年破坏概率的密度。将不同加载工况下极限状态1 和状态3 对应的密度曲线绘于图8。

图8 地震作用下的年破坏概率Fig. 8 Seismic-induced annual damage probability

对图8 中的密度曲线进行积分，即式(15)，可确定不同加载方向对应的总年破坏概率，如图9所示。从图中不难发现，对所有的极限状态，X轴对应的破坏概率明显大于沿Y轴的概率值，与易损性结果呈现相似的变化趋势。

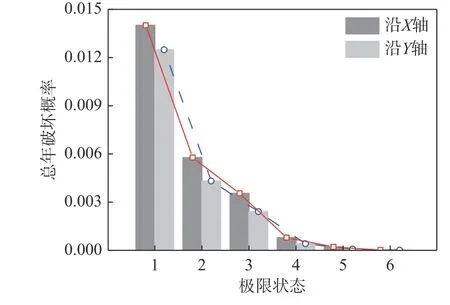
图9 地震作用下的总破坏概率Fig. 9 Seismic-induced total annual damage probability

6 结论

本文提出了基于贝叶斯理论的地震风险评估方法，该分析方法包含了从地震危险性模型建立到结构破坏概率估算的全流程，以中国地震局强震台网中心提供的云南大理地区1970 年-2017 年间仪器实测地震记录和地震目录为研究基础，并以某高层钢框架-RC 核心筒建筑为例，详细介绍了本文所提出的风险评估方法。在分析过程中，综合考虑了地震危险性模型、输入地震动记录、材料参数、阻尼比和需求模型参数不确定性的影响。主要结论如下：

(1) 在传统概率地震危险性分析的基础上，提出了基于贝叶斯理论的地震危险性分析方法，用以考虑对PGA 概率模型认知不确定性的影响。通过与传统方法对比发现，基于贝叶斯理论的方法可以得到更为合理的地震危险性模型。本文立足于我国丰富的地震目录资料和强震台网中心提供的实测数据，这对提升我国现有地震数据的利用效率，以及推动地震危险性评估研究均有一定借鉴意义。

(2) 通过贝叶斯理论建立了基于概率的地震需求模型，在地震易损性分析中考虑了对需求模型认知不确定性的影响。通过与未考虑需求模型不确定性的易损性曲线对比发现，忽略需求模型中参数不确定性将错误估计高层建筑的地震易损性。

(3) 地震动加载方向对高层建筑的年破坏概率存在显著影响，且随着极限状态强度的增加，年破坏概率大幅减小。因此，在高层建筑的地震风险评估时，应综合考虑不同加载方向的影响。