弯折裂纹尖端应力强度因子值的近似计算方法

汪自扬，杨立云，吴云霄，林长宇

(中国矿业大学(北京)力学与建筑工程学院，北京 100083)

断裂力学的发展建立在直裂纹的基础上[1]，当裂纹承受Ⅰ型荷载时，直裂纹沿着裂纹所在轴线扩展，当裂纹承受混合荷载时，直裂纹的扩展路径将会发生不同程度的弯折、弯曲甚至产生分叉现象[2-3]。关于不同形态的裂纹以及裂纹在不同工况下的计算方法有很多[4-6]，通常来说，计算直裂纹的应力强度因子表达式并不适用于计算非直裂纹的情况，但是由于计算非直裂纹的表达式及方法需要运用大量复杂的数学及计算方法[7-9]，例如：弯折、分支裂纹尖端应力强度因子的计算方法可以归纳为两大类[10]：第一类是保角映射法[11]，将分支裂纹映射到单位元上，通过边界条件得到多个积分方程，从而解得裂纹尖端应力强度因子值；第二类是位错方法[12]，即列出奇异积分方程，通过求积分的方法进行数值求解。但是这些方法的缺点是计算量较大，不能够对非直裂纹尖端应力强度因子进行简单快速的求解。

大量学者认为，可以应用简单的直裂纹对非直裂纹进行近似计算，即将非直裂纹通过近似方法转化为相对应的等效直裂纹，通过计算等效直裂纹，得到非直裂纹的解。这种近似方法被许多学者研究并应用，如Kitagawa 等[13]对中心弯曲、弯折和分支裂纹进行研究，并提出在一定的裂纹长度和偏转角度范围内，弯折裂纹尖端应力强度因子(K)值取对应等效直裂纹尖端K值作为理论值的方法是符合精度要求的，特别指出，当分支裂纹长度极小时，由于主次裂纹间的相互作用问题，该近似方法的计算误差较大。Noda 等[14-15]在此基础上通过超奇异积分方程对边缘弯曲裂纹进行研究，结果表明，在Ⅰ型荷载作用下，边缘弯曲裂纹可以应用具有相同投影长度和尖端偏转角的直裂纹进行近似计算。Chen 等[16-17]提出了一个可以计算任意形状裂纹的模型，该模型将任意形状的裂纹分割成多个直裂纹的形式，然后应用复应力势将所受荷载与裂纹尖端的张开位移联系起来进行计算。还有一些研究表明，在某些特定的裂纹形状和荷载形式下，可以将非直裂纹尖端K近似为简单直裂纹形状参数的函数[18-19]，并且认为对于将复杂形状裂纹近似为等效直裂纹的方法是可取的。Tilbrook 和Hoffman[1]研究了非直裂纹的形状参数对断裂参数的影响，认为计算弯曲裂纹尖端的应力强度因子是复杂的，应用等效直裂纹可以大大简化计算过程，并且通过算例很好地解释了为什么直裂纹可以作为等效模型来近似计算弯曲、弯折裂纹的问题。

通过以上观点可以认为，通过建立等效直裂纹模型来近似计算弯折裂纹的近似方法是便捷的。但是，以上文献所提出的关于将弯折裂纹近似为等效直裂纹的方法太单一，提出的可近似计算范围比较笼统，在某些范围内精度不够高，误差较大。所以本文在以上研究的基础上，新提出了三种将弯折裂纹近似为等效直裂纹的近似方法，相比已有近似方法，扩大了可应用近似方法的适用范围，解决了获得等效直裂纹方法单一、近似计算的范围太笼统的问题，并且使近似计算结果的误差进一步缩小。为能够简单快速地在实际工程中计算出不同形状参数下的弯折裂纹尖端K值提供理论参考和方法指导。

1 力学模型与计算方法

1.1 计算模型

为了能清晰地对弯折裂纹进行分析，特建立弯折裂纹力学模型，并将弯折裂纹模型应用几个形状参数进行表示，从而可以应用形状参数求解应力强度因子。图1 为本文所研究的弯折裂纹模型，远场承受单轴拉伸应力σ，其他具体的形状参数OA为弯折裂纹主裂纹，长度为a，与荷载σ 所在方向的锐角夹角(下文所说夹角均为锐角夹角，简称夹角)为β；OB为弯折裂纹次裂纹，长度为b，与荷载σ 所在方向的夹角为α；由此引入图1 中未表示的参数θ，为次裂纹OB与主裂纹OA之间的夹角，称为弯折角，表示为θ=β-α。

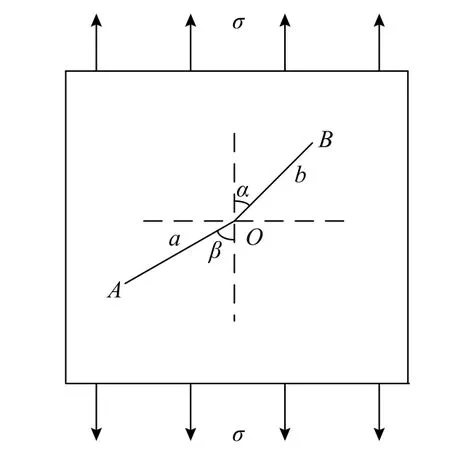
图1 弯折裂纹形状参数示例图Fig. 1 Sample diagram of bending crack geometry parameters

1.2 近似计算方法

本文将弯折裂纹模型按照不同的近似方法近似为等效直裂纹。方法1 为文献[13]中所提出的近似方法，方法2、方法3、方法4 为本文新提出的近似方法。近似方法不同，所得到的等效直裂纹也不同。下面应用这四种近似方法对弯折裂纹尖端A、B分别进行分析。

1.2.1 方法1：水平投影法

参考文献[13]的近似方法可知，当计算弯折裂纹主裂纹尖端A的K时，具体方法是：将次裂纹OB向水平方向(将垂直于荷载方向的轴所在方向定义为水平方向)做投影，投射线与OA反向延长线交于点B1，将直线AB1 作为通过水平投影法得到的计算尖端A的等效直裂纹。等效直裂纹AB1 的长度c11由式(1)计算得到，与荷载所在方向的夹角为η=β，图2 为水平投影法推演图。

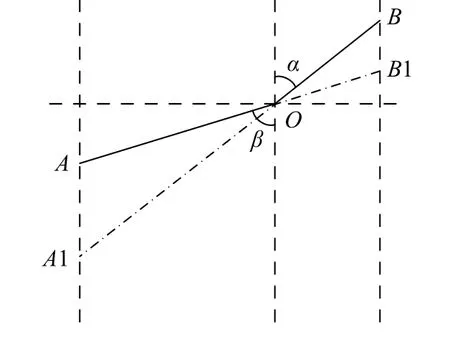
图2 方法1 推演图Fig. 2 Method 1 inference diagram

当计算弯折裂纹尖端B的K时，方法是将弯折裂纹主裂纹OA向水平方向做投影，投射线与OB反向延长线交于点A1，将直线A1B作为通过水平投影法得到的计算尖端B的等效直裂纹。等效直裂纹A1B的长度c12由式(2)计算得到，与荷载所在方向的夹角为η=α。

该方法在文献[13]中表明：当主次裂纹长度比b/a＞0.3，且偏转角θ＜45°时，该近似方法适用。

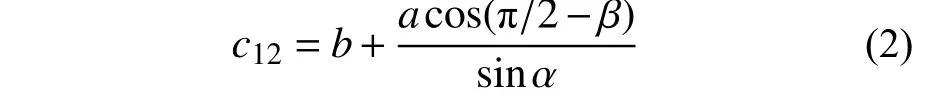
式中：c11为计算裂纹尖端A时的等效直裂纹长度；c12为计算裂纹尖端B时的等效直裂纹长度；其他参数含义同上。

1.2.2 方法2：垂线投影法

当计算弯折裂纹尖端A时，垂线投影法的具体方法是：将次裂纹OB向OA所在方向的反向延长线做垂直投影，垂线与OA反向延长线相交于点B2，将直线AB2 作为通过垂线投影法得到的计算裂纹尖端A的等效直裂纹。等效直裂纹AB2 的长度c21由式(3)计算得到，与荷载所在方向的夹角为η=β，图3 为垂线投影法推演图。

图3 方法2 推演图Fig. 3 Method 2 inference diagram

当计算弯折裂纹尖端B时，将主裂纹OA向OB所在方向的反向延长线做垂直投影，垂线与OB反向延长线相交于点A2，将直线A2B作为通过垂线投影法得到的计算裂纹尖端B的等效直裂纹。等效直裂纹A2B的长度c22由式(4)计算得到，与荷载所在方向的夹角为η=α。

式中：c21为计算裂纹尖端A时的等效直裂纹长度；c22为计算裂纹尖端B时的等效直裂纹长度。其他参数含义同上。

1.2.3 方法3：中心旋转法

当计算弯折裂纹尖端A时，中心旋转法是将次裂纹OB绕点O向OA所在方向的反向延长线一侧做旋转，即将B点旋转至重合点B3 点，旋转角度为主裂纹OA与次裂纹OB之间的夹角θ，得到直线AB3，将直线AB3 作为通过中心旋转法得到的计算裂纹尖端A的等效直裂纹。等效直裂纹AB3 的长度c31由式(5)计算得到，与荷载所在方向的夹角为η=β，图4 为中心旋转法推演图。

图4 方法3 推演图Fig. 4 Method 3 inference diagram

当计算弯折裂纹尖端B时，将主裂纹OA绕点O向OB所在方向的反向延长线一侧做旋转，即将A点旋转至重合点A3 点，旋转角度为主裂纹OA与次裂纹OB之间的夹角θ，得到直线A3B，将直线A3B作为通过中心旋转法得到的计算裂纹尖端B的等效直裂纹。等效直裂纹A3B的长度c32由式(5)计算得到，与荷载所在方向的夹角为η=α。

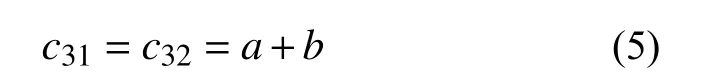
式中：c31为计算裂纹尖端A时的等效直裂纹长度；c32为计算裂纹尖端B时的等效直裂纹长度。其他参数含义同上。

1.2.4 方法4：连线法

连线法的具体方法是：将弯折裂纹主裂纹尖端A与次裂纹尖端B相连，无论计算尖端A还是尖端B，均能够得到等效直裂纹A4B4。该方法得到的等效直裂纹长度c4根据式(6)进行计算，与荷载所在方向的夹角η 根据式(7)计算得到，图5为连线法推演图。

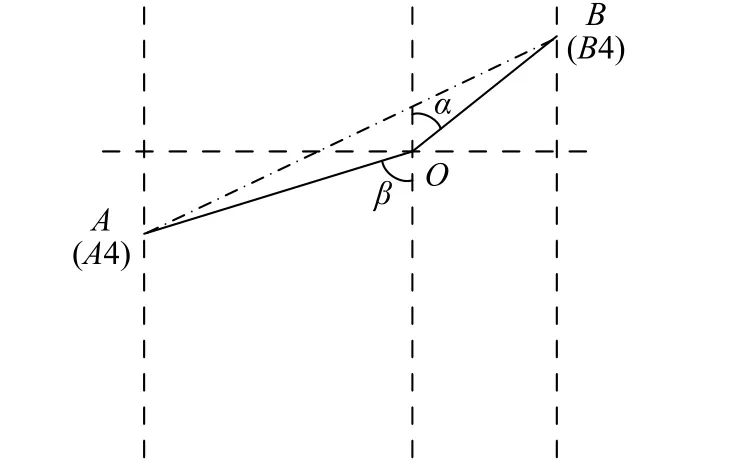
图5 方法4 推演图Fig. 5 Method 4 inference diagram

2 应力强度因子计算

查阅应力强度因子手册，应用Westergaard 应力函数法得到倾斜直裂纹尖端应力强度因子的精确解[20-21]。无限大板中心含倾斜直裂纹，远端承受单轴拉伸荷载，其尖端应力强度因子值的计算式如式(8)所示：

式中：KⅠ、KⅡ为裂纹尖端应力强度因子；σ 为远场拉应力；c为倾斜直裂纹长度；η 为倾斜直裂纹与荷载所在方向的夹角。

根据式(8)可得到各近似方法下的等效直裂纹尖端应力强度因子的计算式，图6 为无限大板中心含倾斜裂纹示意图。

图6 无限大板中心含倾斜裂纹Fig. 6 Inclined crack in the center of infinite plate

A端：将式(1)、式(3)、式(5)代入式(8)，得到计算等效直裂纹尖端A的K值式(9)～式(11)：

B端：将式(2)、式(4)、式(5)代入式(8)，得到计算等效直裂纹尖端B的K值式(12)～式(14)：

不论计算裂纹尖端A还是裂纹尖端B，应用方法4 只能推演出一条等效直裂纹A4B4。将式(6)、式(7)代入式(8)，得到计算等效直裂纹尖端应力强度因子式(15)。

通过推导出来的公式可知，当得到远场拉伸荷载σ、和裂纹各形状参数(a、b、α、β)并代入式(9)～式(15)，即可求得等效直裂纹尖端应力强度因子值。

3 有限元模型

本文基于有限元软件ABAQUS 对二维平面应力条件下不同形状参数的弯折裂纹模型进行计算分析，网格采用八结点双向二次平面应力四边形(CPS8)单元[22]。为了得到更为精确的裂纹尖端应力强度因子值，在裂纹尖端处进行网格加密处理，如图7 所示，模型节点个数为176 144 个，单元个数为59 340 个，使得裂纹尖端区域单元尺寸为初始裂纹长度的0.1%，这便有效地控制了结果的精度要求[23]。裂纹尖端附近环状区域内的单元采用奇异单元以满足裂纹尖端附近应力场平方根的奇异性[24]，本文使用静力、通用分析步，收敛准则采用力的收敛，计算一个模型耗时90 s 左右，从计算结果来看，该计算结果是收敛的。

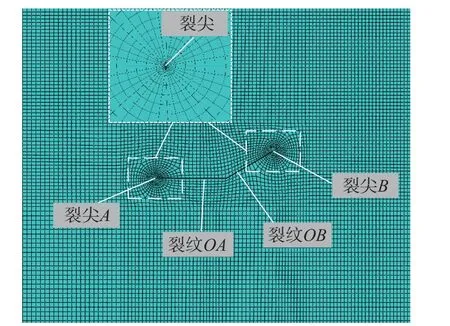
图7 有限元网格图(a=20, b/a =1.5, α=30°, β=90°)Fig. 7 Finite element mesh diagram(a=20, b/a=1.5, α=30°, β=90°)

本文所使用的数值模拟硬件平台基本配置为：CPU 型号为i5-5200U，双核，64 位操作系统，安装内存(RAM)为4 GB，该硬件平台满足计算要求，对计算结果无影响。

板的大小：长×宽=2100 mm×1200 mm，弹性模量：E=2.95 GPa，泊松比：ν=0.2，上下边界施加拉伸荷载σ=4 MPa。基于有限元软件ABAQUS中的相互积分法[25]，直接输出应力强度因子值。

研究过程中，对弯折裂纹进行焦散线试验，计算得到弯折裂纹尖端应力强度因子值，具体的焦散线试验原理和方法参见文献[26]，具体细节不展开讨论。图8 所示为试验中弯折裂纹(b/a=0.8、α=60°、β=90°)的焦散斑图像，根据裂纹尖端焦散斑计算得到裂尖B的KⅠ= 23.51 MPa·mm1/2，KⅡ=14.66 MPa·mm1/2。对试验模型进行数值仿真，得到对应的数值计算结果为：KⅠ= 23.69 MPa·mm1/2，KⅡ= 14.72 MPa·mm1/2。试验结果和数值结果基本吻合，差值不超过1%，验证了数值计算方法的准确性。

图8 弯折裂纹尖端焦散斑图像Fig. 8 Caustics image of bending crack tip

表1 给出了各组弯折裂纹模型的形状参数，共设置六组弯折裂纹模型，模型1、模型2、模型3、模型4 的变量为次裂纹OB与荷载所在方向的夹角α，研究当α 分别为30°、45°、60°、75°时各近似方法的最优情况。设置模型5、模型6 与模型2 形成对照组，分析当α=45°，主裂纹OA与荷载所在方向夹角β 分别为30°、60°、90°时，各近似方法的最优情况。

表1 模型形状参数表Table 1 Model geometry parameter table

4 分析与讨论

应用近似方法计算得到等效直裂纹尖端K值作为弯折裂纹尖端K值的预测值与有限元数值模拟求得的K值进行对比，为了能够清晰地了解各近似方法的准确性和适用性，以下将对弯折裂纹尖端A的KⅠ、KⅡ和弯折裂纹尖端B的KⅠ、KⅡ分别进行分析。

为了能够对近似计算有一个定量的分析，本文将应用近似方法得到的预测K值与有限元数值模拟得到的K值之间进行量化分析，具体指标为误差值，用来衡量误差的大小。但是对于当β=90°的情况，应用方法1、方法2、方法3 进行近似计算，裂纹尖端A的KⅡ预测值均为零，应用误差值不能够进行较好的衡量，所以应用差值作为参考标准，具体定义如下：

4.1 A 端KⅠ值

图9 为裂纹尖端A的KⅠ值随参数b/a的变化曲线。总体来看，当b/a取极小值时，四种方法的K曲线与数值模拟的K曲线重合度较好，但随着b/a的增大，各近似方法的K曲线均呈现不同程度的远离数值模拟K曲线，可以看出，形状参数b/a对近似结果有很大影响。观察图9(a)～图9(d)，随着形状参数α 的增大，四种近似方法的曲线偏离程度逐渐变小，可以得到：尖端A的KⅠ值受形状参数α 影响较大，且形状参数越接近直裂纹的弯折裂纹，近似结果越准确。

如图9(a)～图9(d)，当β=90°，α=30°、α=45°时，近似方法2 的K曲线与数值模拟K曲线重合度最高，相比已有近似方法1，误差值更小。随着α 不断增大，当α=60°、α=75°时，方法3 的误差值最小，最大误差值不超过2%。

图9 裂尖A 的KⅠ 随参数b/a 的变化曲线Fig. 9 Crack tip A of KⅠ curve along with the change of parameter b/a

如图9(e)、图9(f)，当α=45°，β=90°、β=60°时，方法2 的误差值较小，当β=30°时，方法1 要比新提出的三种近似方法适用，所以当β 值较大时，应用方法2，β 较小时，应用方法1，可以减小近似的误差值，使近似结果更为准确。通过对裂纹尖端A的KⅠ值近似计算进行分析，各近似方法的适用范围及误差总结见表2。

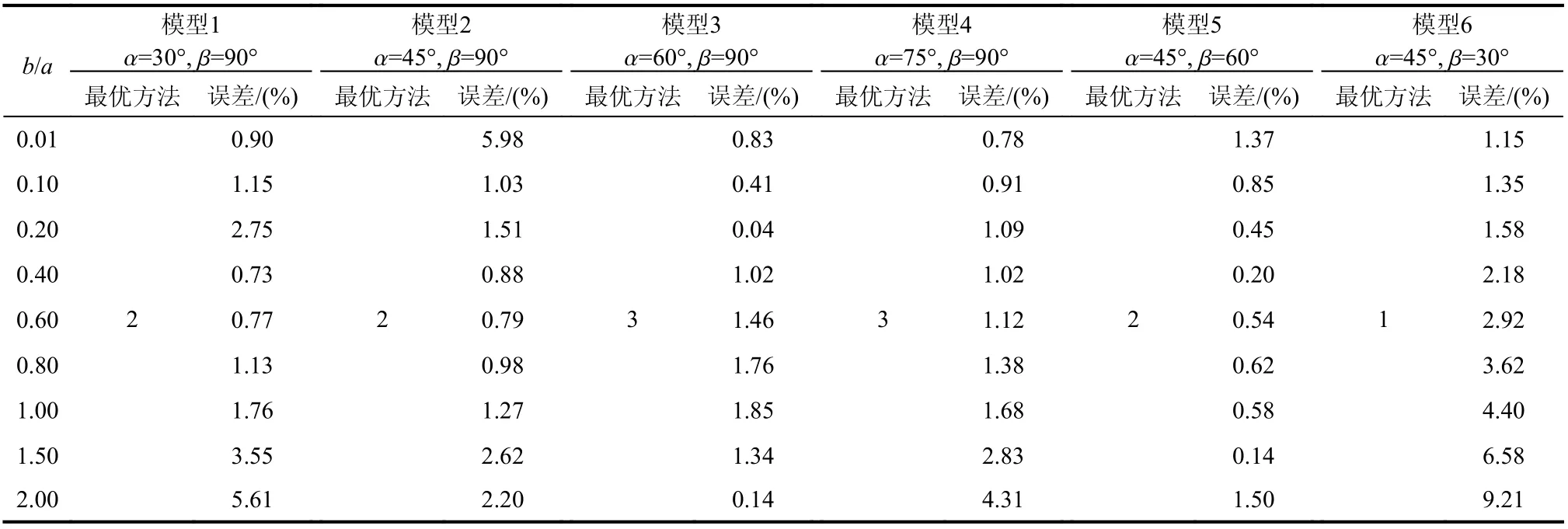
表2 裂尖A 的KⅠ 近似方法Table 2 KⅠ approximation method for crack tip A

4.2 A 端KⅡ值

图10 为裂纹尖端A的KⅡ值随参数b/a的变化曲线。如图10(a)～图10(d)，方法4 的K曲线偏离较大，不考虑。方法1、方法2、方法3 的K曲线与数值模拟K曲线重合度较高，且不受形状参数α、b/a的影响。但观察图10(b)、图10(e)、图10(f)，当α 不变，β 变化时，对曲线的重合度影响较大。所以得出，形状参数β 是影响裂尖A的KⅡ值近似计算的主要因素。

如图10(a)～图10(d)，方法1、方法2、方法3对于裂尖A的KⅡ值的近似计算结果差值均较小，当b/a＜1.5，最大差值不超过一个计量单位，所以可以应用方法1、方法2、方法3 对当β=90°情况下的尖端A的KⅡ值进行近似计算。

如 图10(b)、图10(e)、图10(f)，当α=45°，β=90°、β=60°时，原近似方法1 误差较小，但当β=30°时，方法4 的近似结果更为准确，从表3 可以看出，方法4 在形状参数0.1＜b/a＜1 的区间内，近似计算的误差值非常小。所以认为方法4 适用于近似计算β 值较小(即主裂纹所在方向平行于荷载所在方向)情况下的A端KⅡ值。

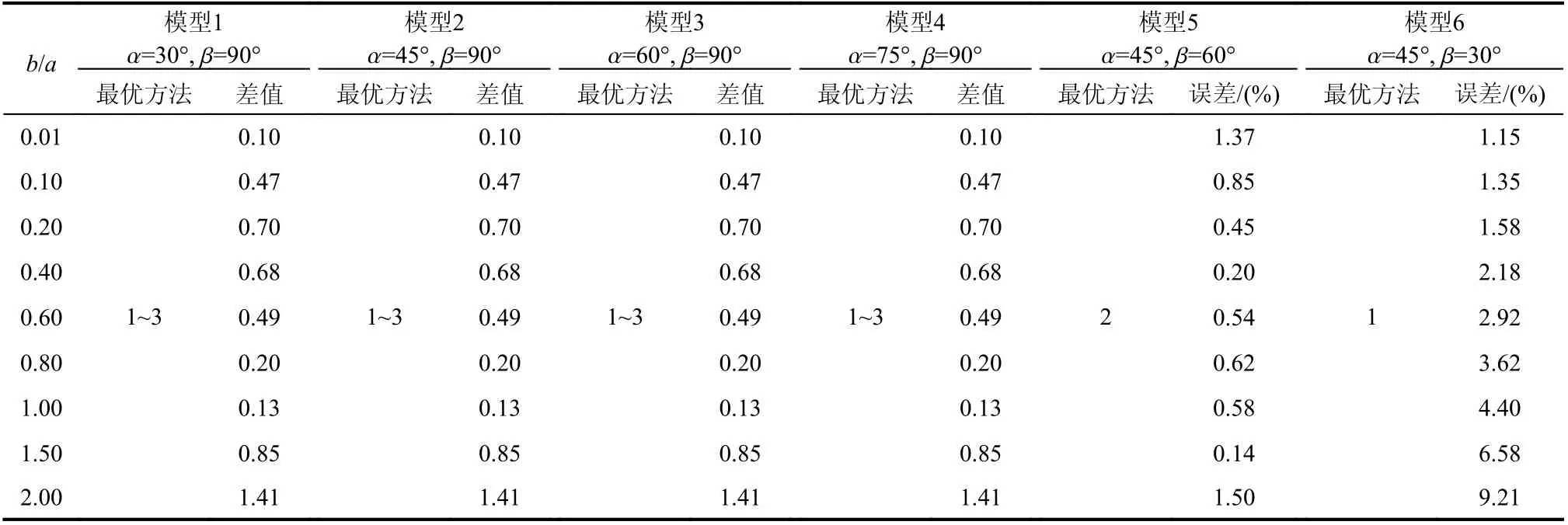
表3 裂尖A 的KⅡ近似方法Table 3 KⅡ approximation method for crack tip A

图10 裂尖A 的KⅡ随参数b/a 的变化曲线Fig. 10 Crack tip A of KⅡ curve along with the change of parameter b/a

4.3 B 端KⅠ值

图11 为裂纹尖端B的KⅠ值随参数b/a的变化曲线。总体来看，形状参数α、β、b/a对K曲线均有影响。当β=90°时，α 不论取什么值，方法1始终为最优方法，但是从误差值来看，结果并不理想。参考图11(a)，当α=30°时最大误差值高达42.82%，即在该几何参数下的弯折裂纹不宜应用等效直裂纹进行近似计算，这是由于弯折角度θ 较大，主次裂纹尖端的相互作用所导致的，与文献[13]中的相关结论一致。观察图11(c)、图11(d)、图11(e)，随着α 不断增大，误差值逐渐减小，所以得出：形状参数α 是影响近似计算裂尖B的KⅠ值的最主要因素。

参照图11(b)、图11(e)、图11(f)，当α=45°，β 取不同的值，方法1 为最优方法，误差值随形状参数b/a变化较大。可以发现，当形状参数b/a较大时，近似方法1 的近似计算误差值会增大，新提出的近似方法可替代近似方法1 进行近似计算。具体的最优近似方法和误差见表4。

表4 裂尖B 的KⅠ近似方法Table 4 Crack tip B of KⅠ approximate solution

图11 裂尖B 的KⅠ 随参数b/a 的变化曲线Fig. 11 Crack tip B of KⅠ curve along with the change of parameter b/a

4.4 B 端KⅡ值

图12 为裂纹尖端B的KⅡ值随参数b/a的变化曲线。总体来看，K曲线的大体趋势相同，受形状参数的影响，多条K曲线的聚合程度不同，随着形状参数α 的增大或者β 的减小，各种近似方法的K曲线相互靠拢，所以得出结论：越接近直线的弯折裂纹，近似方法的适用性更强。从表5可以发现，当β=90°时，各近似方法的近似计算误差都较大，所以该参数下的弯折裂纹模型不适合应用近似方法进行近似计算。但随着β 逐渐减小，近似计算的误差逐渐减小，所以形状参数β 是影响裂纹尖端B的KⅡ值的主要因素。

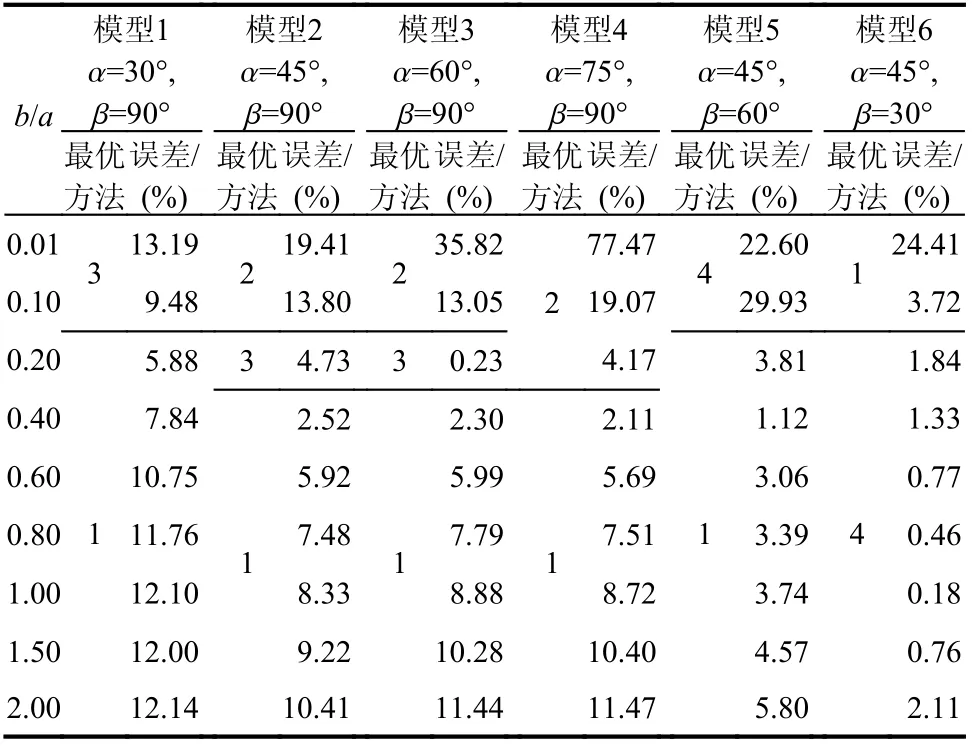
表5 裂尖B 的KⅡ近似方法Table 5 Crack tip B of KⅡ approximate solution

参考图12，当0＜b/a＜0.3，数值模拟K曲线呈现出突增的趋势，在该区域内，次裂纹长度的微增量便引起了KⅡ值的显著增大，根据文献[13]的相关结论可知，主要原因是：当次裂纹长度较小时，次裂纹尖端应力场受主裂纹影响较大。相比较原有近似方法1，近似方法2、方法3，在该区间内的近似结果较好。当β=90°，0.3＜b/a＜2.0，方法1 为最优方法，但是，近似计算的误差较大。

图12 裂尖B 的KⅡ随参数b/a 的变化曲线Fig. 12 Crack tip B of KⅡ curve along with the change of parameter b/a

参考图12(b)、图12(e)、图12(f)，当β=90°、β=60°时，方法1 的近似计算结果误差较大。当β=30°时，近似方法4 的近似计算误差较小，在该形状参数下，方法4 为最优方法。结合裂尖A的KⅡ近似计算结果可以得到的结论是：近似方法4适用于形状参数β 值较小的弯折裂纹的近似计算，并且近似计算的误差值较小。

5 结论

本文将弯折裂纹模型通过近似方法近似为等效直裂纹，通过计算等效直裂纹得到弯折裂纹尖端应力强度因子值。根据已有的近似方法新提出了三种计算弯折裂纹的近似方法，并将计算结果与数值模拟值进行对比，得到以下结论：

(1)新提出的三种近似方法同已有近似方法相比，丰富了得到等效直裂纹的手段，使得到等效直裂纹的方式不再单一；扩大了使用等效直裂纹计算弯折裂纹尖端应力强度因子的近似方法的范围；而且提出了在不同形状参数下近似方法的最优情况，使得近似计算的精度更高。

(2)当计算弯折裂纹主裂纹尖端Ⅰ型应力强度因子 (KⅠ) 时：主裂纹与荷载所在方向垂直，且次裂纹与荷载所在方向的夹角小于45°，垂线投影法比水平投影法的近似计算精度高；当次裂纹与荷载所在方向的夹角大于45°时，中心旋转法为最优近似方法。当计算弯折裂纹主裂纹尖端KⅡ时，垂线投影法、中心旋转法均能够得到精度较高的计算结果。通过分析可知：由于主次裂纹间的相互作用，对次裂纹尖端K值的近似计算结果并不理想，当计算弯折裂纹次裂纹尖端KⅠ时，在主次裂纹长度比b/a较大时，新提出的近似方法比已有近似方法更适用。综合来看，连线法适用于计算当主裂纹与荷载所在方向夹角较小的弯折裂纹，而且近似计算结果的精度很高。

(3)对弯折裂纹主裂纹尖端的近似计算结果精度较高；但由于主次裂纹间的相互作用，弯折裂纹次裂纹尖端的近似计算结果精度较低，尤其是当主次裂纹长度比b/a较小时，受弯折裂纹的裂纹长度影响较大。弯折裂纹主裂纹OA与荷载所在方向的夹角β 是影响KⅡ近似计算结果精度的主要因素；弯折裂纹次裂纹OB与荷载所在方向的夹角α 是影响KⅠ近似计算结果精度的主要因素。