基于变弹性模量的Ti-6Al-4V板材五点弯曲回弹预测
2022-09-03孟智娟马立东
屈 聪 孟智娟 赵 亮 陈 耀 马立东
太原科技大学机械工程学院,太原,030000
0 引言
Ti-6Al-4V钛合金具有质量小、强度高、耐腐蚀和耐疲劳等优越的性能,在航空、军事、医学等[1-3]领域得到了广泛的应用。但因其具有较高的屈服强度和较低的弹性模量,使得Ti-6Al-4V在弯曲成形过程中的回弹难以控制,所以预测弯曲回弹对产品质量具有重要的意义。国内学者在弯曲回弹理论方面做了大量研究。赵军等[4]建立了平面弯曲弹复方程,并将其成功地应用于扩径矫圆工艺。在此基础上,ZHAO等[5-6]对大型管道的管端整修过程中回弹的预测和控制进行了研究,并通过预紧力和弯矩的加载方法对型材平面拉伸弯曲的回弹分析进行了研究。段永川等[7]建立了V形小曲率自由弯曲回弹的解析预测模型,利用此模型分析了不同工艺参数对V形自由弯曲力和回弹后弯曲角度的影响规律,确定了弯曲力和回弹角的主要影响因素。马瑞等[8]针对板材回弹问题,建立了迭代补偿机制,并将此工艺应用于宽板自由弯曲工艺的回弹控制,根据每次实验的回弹量,迭代补偿机制可以预测下一次的补偿值。李佼佼等[9]建立了三点弯曲有限元模型,研究了不同厚度、不同温度下Invar30合金厚板的回弹规律。MA等[10]分析了ERW管FFX预制段的五点弯曲过程和回弹过程,建立了五点弯曲回弹力学模型。吴义江等[11]以高强钢厚板冷弯成形为研究对象,利用数值仿真方法对回弹的影响参数进行了分析。
目前有很多学者使用有限元模拟的形式来预测成形过程中的回弹。有限元模拟与实际情况也存在一定的误差,这与所构建的模型、单元的划分、材料本构设置、边界条件设置等都有关系,其中材料本构模型尤为重要。BARLAT等[12]提出了一个各向异性屈服准则,适用于平面应力条件,能够描述板料变形时的面内各向异性。BARLAT等[13]又提出了YLD2000-2D屈服准则并应用于铝合金板材成形过程有限元分析中。NAOFAL等[14]基于Y-U硬化模型及变弹性模量对板材辊弯成形过程回弹预测进行了研究,结果表明,硬化模型及弹性模量变化对回弹预测有很大的影响。FU等[15]针对弯曲成形过程中的回弹问题,利用遗传算法优化权值进而实现理想的弯曲回弹预测和研究。BADR等[16-18]对Ti-6Al-4V钛合金室温辊弯成形进行了研究,提出了一种各向异性的弹塑性本构材料模型,该模型在预测室温下Ti-6Al-4V薄板样品的鲍辛格效应和瞬态硬化行为方面具有更高的准确性,在此基础上他们还研究了辊弯成形方式对Ti-6Al-4V室温辊弯成形回弹的影响。
随着科学技术的进步与制造业的不断发展,人们对回弹预测的精度提出了更高的要求。弹性模量在成形过程中发生变化,从而影响回弹预测的精度,这在回弹问题的研究领域是一个新的研究方向。MORESTIN等[19]通过实验发现,当塑性应变仅为5%时,弹性模量降幅即可达到初始值的10%以上,并且通过所开发的软件计算了冲压工艺中的回弹,该软件考虑了弹性模量的变化,计算结果很接近实验值。YOSHIDA等[20]针对高强钢DP590的材料性能进行了研究,发现当增加预应变时弹性模量出现迅速下降的趋势,并提出了Y-U硬化模型及变弹性模量数学模型。LIU等[21]以超高强钢为研究对象,提出了一种考虑弹性模量变化的数学模型,并将其应用于三维有限元分析(finite element analysis,FEA)中来模拟冷轧成形过程,通过与Swift材料本构模型的对比,使用非线性弹性模量计算出的回弹精度提高了18%。SUN 等[22]针对材料的弯曲回弹行为,建立了QPE模型用来描述弹性模量的非线性变化,该模型提高了弯曲回弹的预测精度。
本文以Ti-6Al-4V钛合金为研究对象,通过单轴拉伸实验与循环加载-卸载实验确定了材料各向异性参数并研究材料五点弯曲变形过程中弹性模量变化规律, 建立了变弹性模量数学模型。基于变弹性模量数学模型及YLD2000-2D屈服准则编写了材料本构模型子程序,利用ABAQUS仿真软件Umat子程序接口将自定义本构模型嵌入有限元模型中,进行了常温下板材五点弯曲回弹数值模型。最后,进行了常温下五点弯曲实验,对比分析了实验结果与模拟结果。
1 材料选取
钛是一种同素异构体,有两种不同的晶体结构,在低于882℃时称为α-Ti,在882℃以上时称为β-Ti,α-Ti为理想的密排六方(HCP)结构,β-Ti呈体心立方晶体结构。Ti-6Al-4V钛合金作为一种具有α+β两相的等轴组织合金,具有良好的综合性能,可以较好地进行热应力加工,也能通过淬火、时效处理使合金强化,其主要构成元素及含量见表1。

表1 材料化学成分(质量分数)
2 实验、数值模拟及本构模型的建立
2.1 单轴拉伸、循环加载-卸载实验
Ti-6Al-4V钛合金材料具有较强的各向异性,为测定Ti-6Al-4V钛合金的材料性能及各向异性系数,进行了准静态单轴拉伸实验。如图1所示,该实验在Instron-5969万能材料实验机(载荷50 kN)上进行。

图1 Instron-5969万能材料实验机Fig.1 Instron-5969 universal material testing machine
分别在材料的RD(轧制方向)、DD(对角线方向)、TD(横向)三个方向进行了拉伸实验。根据实验需求,制作了拉伸试样,试样尺寸及取样方式如图2和图3所示。本实验在常温下进行,拉伸速率为0.01 mm/min,使用接触式引伸计测量变形。
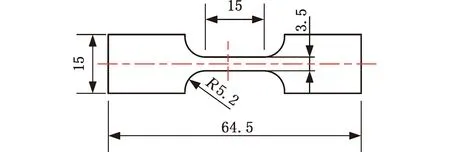
(a)拉伸试样示意图

(b)拉伸试样实物图图2 拉伸试样的尺寸Fig.2 The size of the tensile specimen
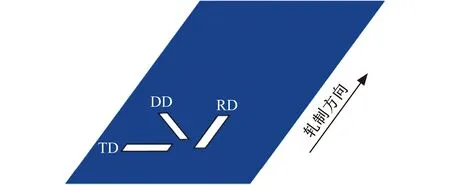
图3 取样方式Fig.3 Sampling method
为测定Ti-6Al-4V钛合金在不同塑性应变下弹性模量的变化规律,对其进行了单轴循环加载-卸载实验。该实验同样在Instron-5969万能材料试验机上进行,实验条件及拉伸试样与单轴准静态拉伸实验相同。单轴循环加载-卸载实验的具体实验步骤如下:将试样加载至所需的初始预应变,停止拉伸,之后将应力卸载为0;再加载至第二个预应变值,停止拉伸,将应力卸载为0,如此循环直到完成最大的预设应变值。预应变设置为:0.8%、1.0%、1.5%、2%、2.5%、3.3%、4.1%、5.1%、6.1%、7.1%、8.1%、9.1%。同理,对RD、DD、TD三个方向的试样进行测试。与其他两个方向相比,TD方向的延伸率较低,为了防止接触式引伸计被损坏,TD方向的试样预应变值仅设置到7.1%。
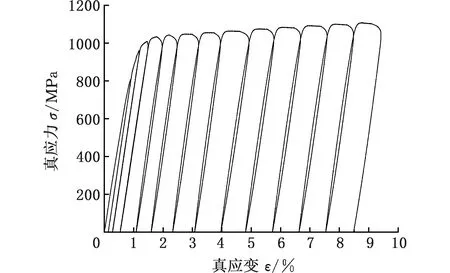
(a)RD方向的应力-应变曲线
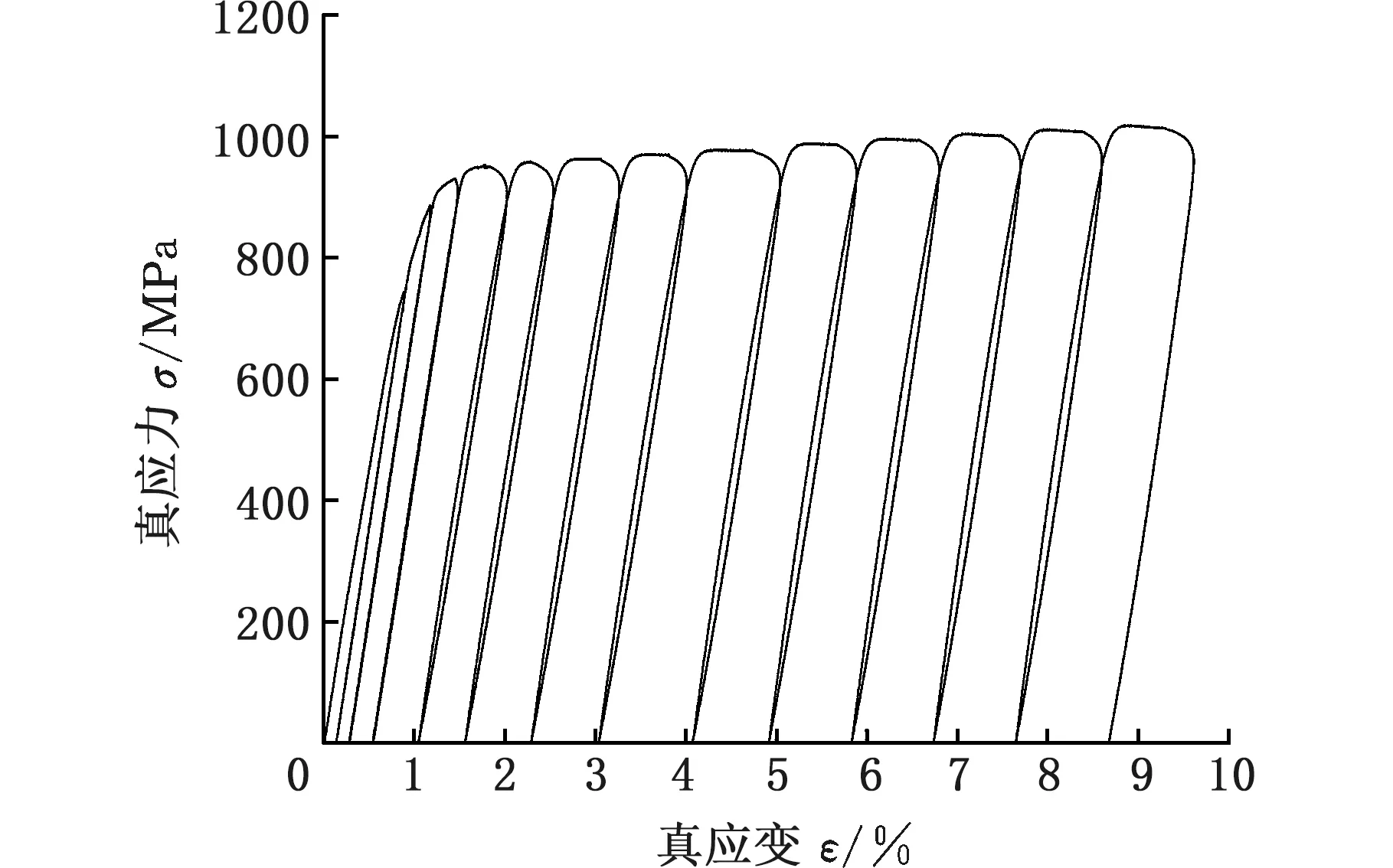
(b)DD方向的应力-应变曲线

(c)TD方向的应力-应变曲线图4 加卸载实验应力-应变曲线Fig.4 Loading-unloading-loading experiment stress-strain curves
2.2 实验结果分析
循环加载-卸载实验所测得RD、DD、TD三个方向的应力应变曲线如图4所示。通过单轴准静态拉伸实验得到了Ti-6Al-4V钛合金RD、DD、TD三个方向的应力-应变曲线,如图5所示。

图5 Ti-6Al-4V钛合金应力-应变曲线Fig.5 Ti-6Al-4V titanium alloy stress-strain curves
本实验测量的Ti-6Al-4V钛合金RD、DD、TD三个方向的弹性模量、0.2%偏移屈服强度、极限抗拉强度、总伸长率和塑性应变比(r值)见表2。
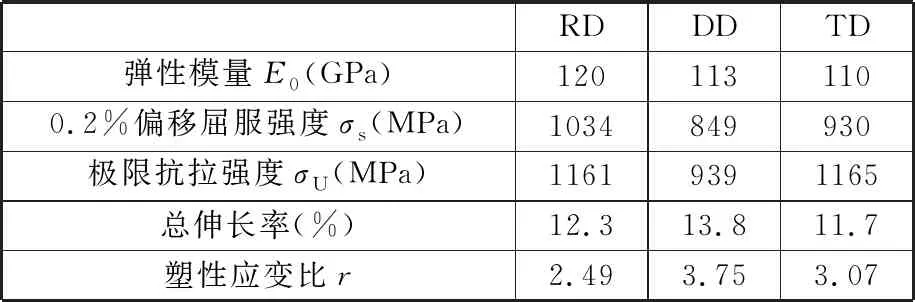
表2 Ti-6Al-4V钛合金单轴拉伸实验的材料参数
r值按以下公式计算:
(1)
式中,εw、εt分别为宽度方向和厚度方向上的应变;w0、w分别为试样的初始宽度和最终宽度;t0、t分别为试样的初始厚度和最终厚度。
2.3 变弹性模量的定义
弹性模量的值在一般的应力-应变曲线中为直线的斜率,由上文单轴循环加载-卸载实验数据可以发现,重新加载的弹性模量具有迟滞特性,弹性模量不能再以简单的取斜率的方式来计算,故一些学者提出了三种弹性模量的计算方式:加载模量、卸载模量、弦线模量。其中,加载模量为二次加载曲线前半段连线的斜率,卸载模量为卸载曲线前半段连线的斜率,弦线模量为前一次最大应变点与后一次起始应变点连线的斜率。NAOFAL等[14]验证了弦线模量比加载模量与卸载模量对预测回弹具有更高的精度,故本文选取弦线模量的计算方式计算加载-卸载曲线中的弹性模量值。弦线模量的计算公式如下:
(2)
式中,σ1、ε1分别为前一次最大应变点的应力、应变值;σ0、ε0分别为后一次起始应变点的应力、应变值。
基于YOSHIDA等[20]提出的变弹性模量数学模型,对以上三个方向的数据点进行拟合。变弹性模量数学模型如下:
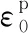
(3)
式中,E0为初始弹性模量;Eav为变形过程中平均弹性模量;Ea为材料参数;ξ为控制弹性模量下降速率的材料参数。
基于以上公式,拟合得到三个方向的变弹性模量公式参数,其中每个方向的参数E0、Ea、ξ见表3。
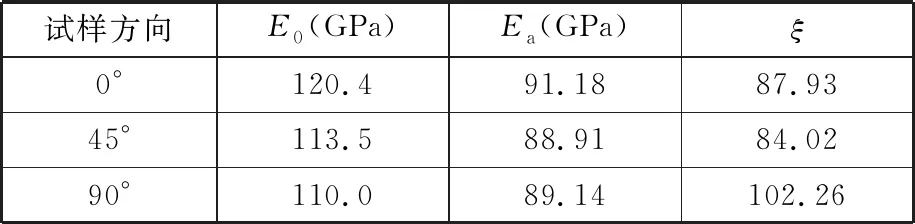
表3 变弹性模量数学模型参数

图6 RD、DD、TD方向的变弹性模量拟合曲线Fig.6 Variable elastic modulus fitting curve for RD, DD, TD
图6为实验数据点与拟合曲线的对比图。RD、DD、TD三个方向的弹性模量随着塑性应变的增加都出现了明显的下降趋势。在3.3%塑性应变之前,弹性模量下降速率较快,而在3.3%塑性应变之后,该下降趋势逐渐趋于平缓,最终成为一个定值。Ti-6Al-4V钛合金的塑性应变为8.3%时,RD方向弹性模量下降了18.9%,DD方向弹性模量下降了22.39%,TD方向弹性模量下降了20%。从图6中可以看出,根据数学模型拟合的曲线与实验数据非常接近,说明数学模型可以很好地描述材料弹性模量变化规律。虽然Ti-6Al-4V钛合金三个方向的变化规律相同,但由于初始弹性模量存在一定的各向异性,导致在整个变形过程中RD方向的弹性模量始终大于另外两个方向的弹性模量,在较大塑性应变下的弹性模量比另外两个方向的弹性模量大10 GPa左右。由于DD方向和TD方向的初始弹性模量相近,并且随着塑性应变增加,它们的弹性模量的变化规律相同,故DD、TD两个方向的弹性模量在变形过程中比较接近。
2.4 YLD2000-2D屈服准则
由于Ti-6Al-4V钛合金在成形过程中表现出较强的各向异性,各向同性屈服准则并不适用,所以本文采用文献[13]中的YLD2000-2D屈服准则。YLD2000-2D屈服准则是建立在平面应力基础上的一个平面屈服准则,它是通过在Cauchy应力张量上使用两个线性变换将材料的各向异性参数引入屈服函数当中。YLD2000-2D屈服准则可以很好地描述Ti-6Al-4V钛合金的屈服行为,且对研究薄板五点弯曲过程(可近似看成二维问题)也非常适用。YLD2000-2D屈服函数表达式如下:
(4)
φ′=|X′1-X′2|a
(5)
φ″=|2X″2+X″1|a+|2X″1+X″2|a
(6)
其中,X′1、X′2,X″1、X″2分别为X′和X″的应力主值,即
(7)
(8)
X′和X″的分量可以通过以下两个线性变换获得:
X′=C′s=C′Tσ=L′σ
(9)
X″=C″s=C″Tσ=L″σ
(10)

(11)
其中,变换矩阵T的作用是将柯西应力σ变换为其对应的偏应力张量s;矩阵C′与C″的作用是引入各向异性参数。即
(12)
(13)
(14)
(15)
(16)
(17)
其中,α1~α8为8个各向异性参数,当这8个参数的值等于1时,该屈服准则就变成了各向同性屈服准则。这8个参数需要通过单轴拉伸实验以及双轴拉伸实验所测得的σ0、σ45、σ90、σb、r0、r45、r90、rb这8个实验数据计算得出,其中,σb、rb由文献[16]给出,其他参数具体计算方式参考文献[13],各向异性参数取值见表4。

表4 YLD2000-2D各向异性参数
2.5 数值模拟
本文采用ABAQUS有限元软件对常温下Ti-6Al-4V钛合金板材五点弯曲过程进行数值模拟。数值模拟共分为两组,分别对应不同的压弯行程y=25 mm,30 mm。模型尺寸及弯曲行程示意图见图7。此数值模拟共分为以下3个分析步:①上模具与板材上层接触;②压弯至指定位置;③上模具上升板材回弹。
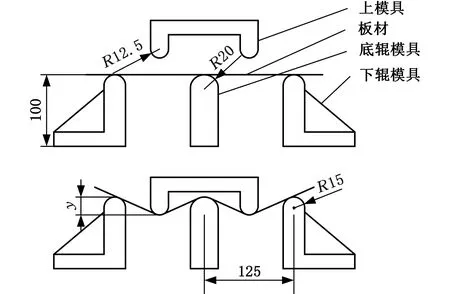
图7 模具尺寸及弯曲行程示意图Fig.7 Schematic diagram of mold size and bending stroke
Ti-6Al-4V钛合金板材五点弯曲有限元模拟三维模型如图8所示。Ti-6Al-4V钛合金板材长330 mm,宽40 mm,厚度2 mm,上模具、底辊模具和下辊模具均设置为离散刚体,板材设置为可变形壳体。
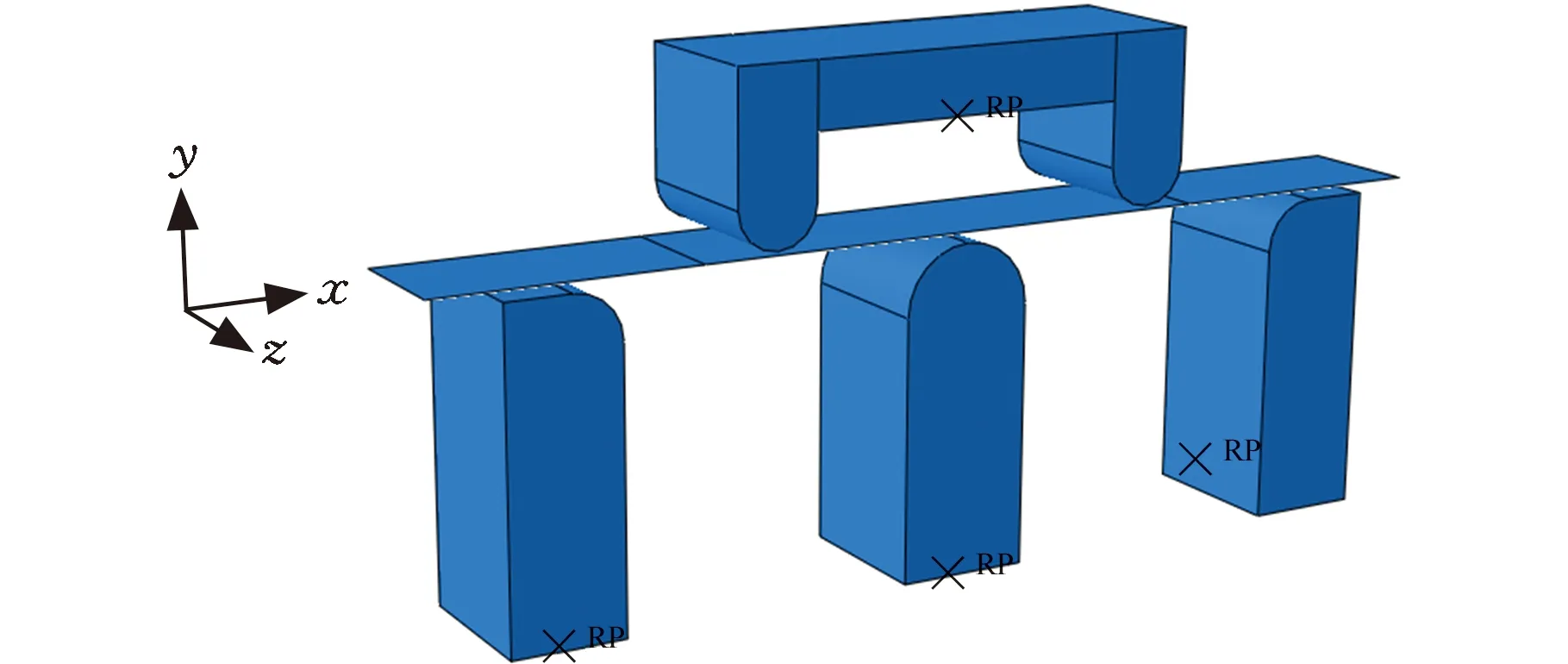
图8 有限元模型Fig.8 Finite element model
ABAQUS具有高度的开放性,当 ABAQUS 材料库中包含的现有本构模型中不能准确地表示要模拟的材料行为时,它为用户提供了自定义材料模型子程序接口,即Umat子程序接口。本文基于以上YLD2000-2D屈服准则及变弹性模量数学模型建立了Ti-6Al-4V钛合金材料本构模型,并通过Umat子程序接口将该模型嵌入ABAQUS软件中。为研究屈服准则及变弹性模量对Ti-6Al-4V板材弯曲回弹预测的影响,本文进行了两种不同本构模型情况下的弯曲回弹模拟。
为了准确描述Ti-6Al-4V钛合金的硬化曲线,本文选择Voce模型来描述其流动应力的变化。对轧制方向的流动应力进行了拟合,拟合结果如下:
(18)
数值模拟中,两种本构模型的材料参数设置见表5。
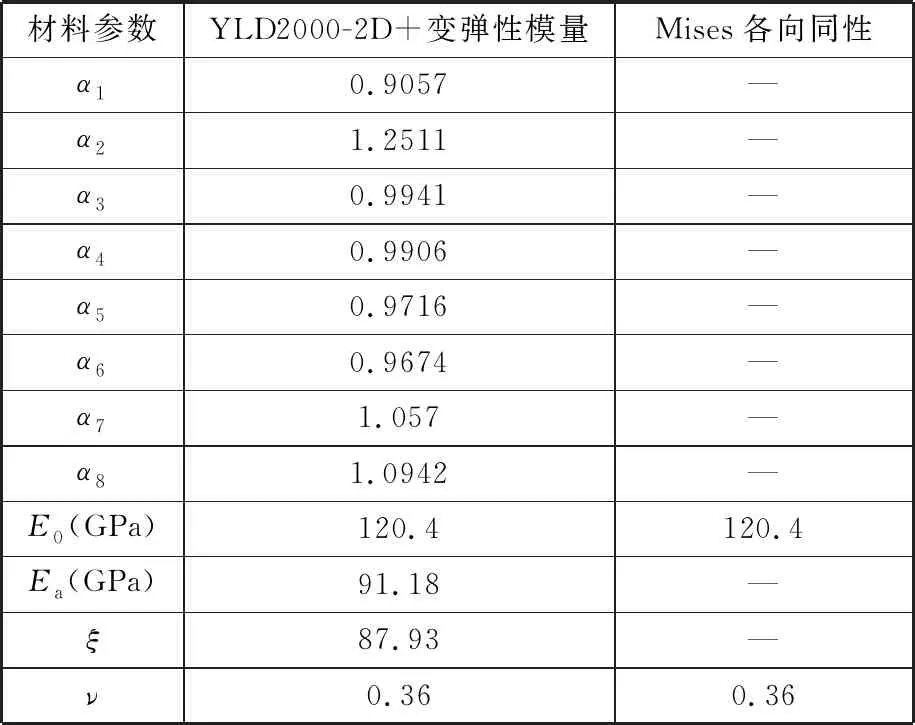
表5 两种本构模型的输入参数
ABAQUS中对模型进行网格划分是决定精度高低的重要环节。网格划分的粗细程度和单元类型的选择都在不同程度上影响着最终的计算结果。YLD2000-2D是基于平面应力状态下的屈服准则,对此板材单元采用S4R四节点壳单元。为了使计算结果的准确度更高,将板材分成两个区域分别设置不同的单元尺寸,其中,变形大的区域网格较精细,变形小的区域网格较粗糙,网格划分如图9所示。
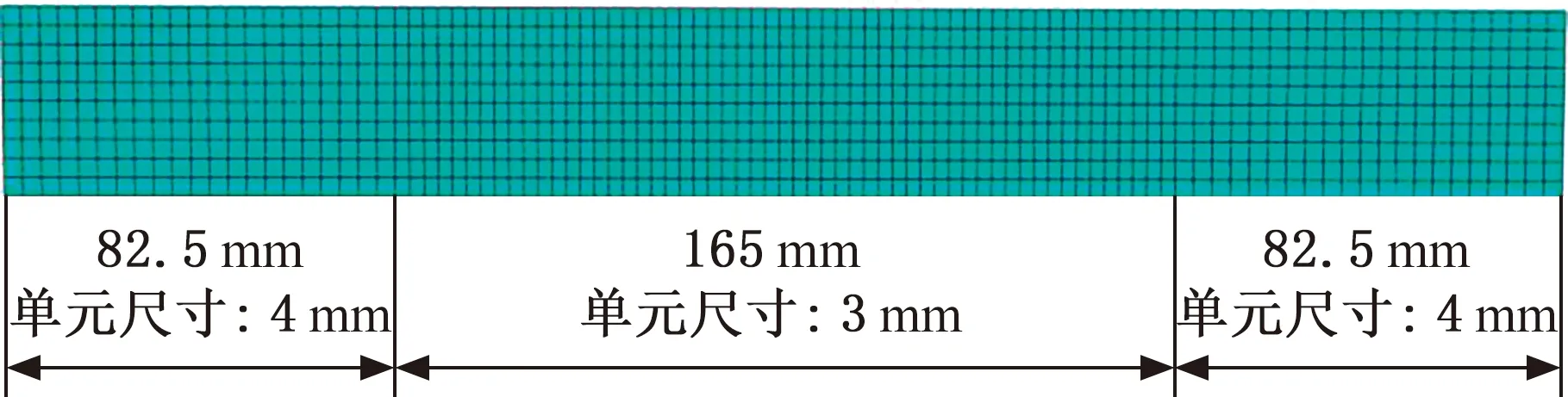
图9 单元划分法Fig.9 Element division method
在接触面设置中,选择面对面接触作为板材与模具之间的接触类型,并且遵循主从面选择,其中定义刚体面为主面,可变形体面为从面。此外对两个面之间的接触定义接触属性,其中,法向属性设置为“硬接触”,切向属性设置为库仑摩擦,设定摩擦因数为0.2。对于边界条件的设置,上下模具需设置参考点,如图8中的RP。下辊和底辊模具在参考点处设置完全固定约束,上模具在参考点处设置y轴方向的位移载荷。
Ti-6Al-4V钛合金由于其弹性模量小,在弯曲的过程中会产生很明显的回弹现象。图10、图11分别为基于子程序本构模型和ABAQUS原有本构模型计算的板材弯曲行程30 mm状态下的横向弹性应变图,可以看出Ti-6Al-4V钛合金板材在卸载后发生了很明显的回弹。在弯曲过程中,发生弹性变形的区域主要集中在板材的中间区域,且在回弹之后弹性应变全部恢复。

(a)回弹前

(b)回弹后图10 弯曲行程为30 mm时基于子程序计算的横向弹性应变云图Fig.10 Transverse elastic strain nephogram based on subroutine calculation when bending stroke is 30 mm
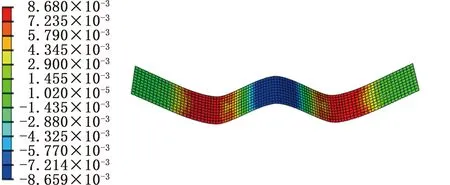
(a)回弹前

(b)回弹后图11 弯曲行程为30 mm时基于原有材料模型计算的横向弹性应变云图Fig.11 Transverse elastic strain nephogram based on original material model when bending stroke is 30 mm
2.6 常温下五点弯曲实验
为验证数值模拟结果的准确性,进行了常温下Ti-6Al-4V钛合金板材五点弯曲实验,本实验在电子万能实验机上进行。如图12所示,先将上模具与板材上表面贴合,之后在操作系统中设置压下量,上模具压下至指定的压下量,最后上模具抬升。实验所用模具如图12所示,分为上模具、下辊模具、底辊模具,模具尺寸与数值模拟中模具的尺寸完全相同。实验所用的Ti-6Al-4V钛合金板材几何参数为330 mm×40 mm×2 mm,板材是以初轧或锻造的板坯为原料经加热、轧制、热矫、热处理、中断、矫形、除磷、酸洗等基本生产过程加工而来的,其中热处理为硬退火。

(a)板材与模具贴合图

(b)板材压弯图图12 五点弯曲实验工艺流程图Fig.12 Process flow chart of five point bending test
本实验中,压下量分别取25 mm和30 mm,实验测得的板材回弹后与水平线夹角θ的示意图见图13。夹角θ的实验数据见表6。

图13 夹角θ的示意图Fig.13 Schematic diagram of included angle θ

表6 不同弯曲行程下板材回弹后与水平线夹角
为了使结果更有说服性,取三次实验的平均值作为后续分析的依据。当压弯行程为25 mm时,板材回弹后与水平线夹角取6.51°;当压弯行程为30 mm时,夹角取11.12°。
3 回弹分析
通过常温下的数值模拟及弯曲实验获知了Ti-6Al-4V钛合金板材在不同压弯行程及不同本构模型下的板材回弹情况。不同本构模型对Ti-6Al-4V钛合金板材五点弯曲回弹预测的影响如图14所示(示意图为板材的左半部分)。图14展示了25 mm和30 mm两种不同弯曲行程下不同本构模型对板材最终弯曲成形效果的影响。弯曲行程相同的情况下,基于Mises各向同性本构模型得到的数值模拟结果与实验结果差距最大。而基于YLD2000-2D屈服准则及变弹性模量本构模型所得的数值模拟结果与实验结果比较接近。25 mm弯曲行程下,Mises各向同性本构模型的模拟结果和实验结果相差2.38°,YLD2000-2D屈服准则及变弹性模量本构模型的模拟结果和实验结果相差0.35°;30 mm弯曲行程下,前者相差4.41°,后者相差1.68°。

(a)弯曲行程25 mm

(b)弯曲行程30 mm图14 基于不同本构模型的数值模拟与实验结果Fig.14 Numerical simulation and experimental results based on different constitutive models
如图15所示,基于YLD2000-2D及变弹性模量本构模型,25 mm压弯行程下,Ti-6Al-4V钛合金板材五点弯曲数值模拟回弹预测精度比Mises各向同性本构模型提高了31.18%;30 mm压弯行程下,回弹预测精度提高了24.55%。综上所述,基于YLD2000-2D及变弹性模量的本构模型可以显著提高Ti-6Al-4V钛合金板材五点弯曲回弹预测精度。
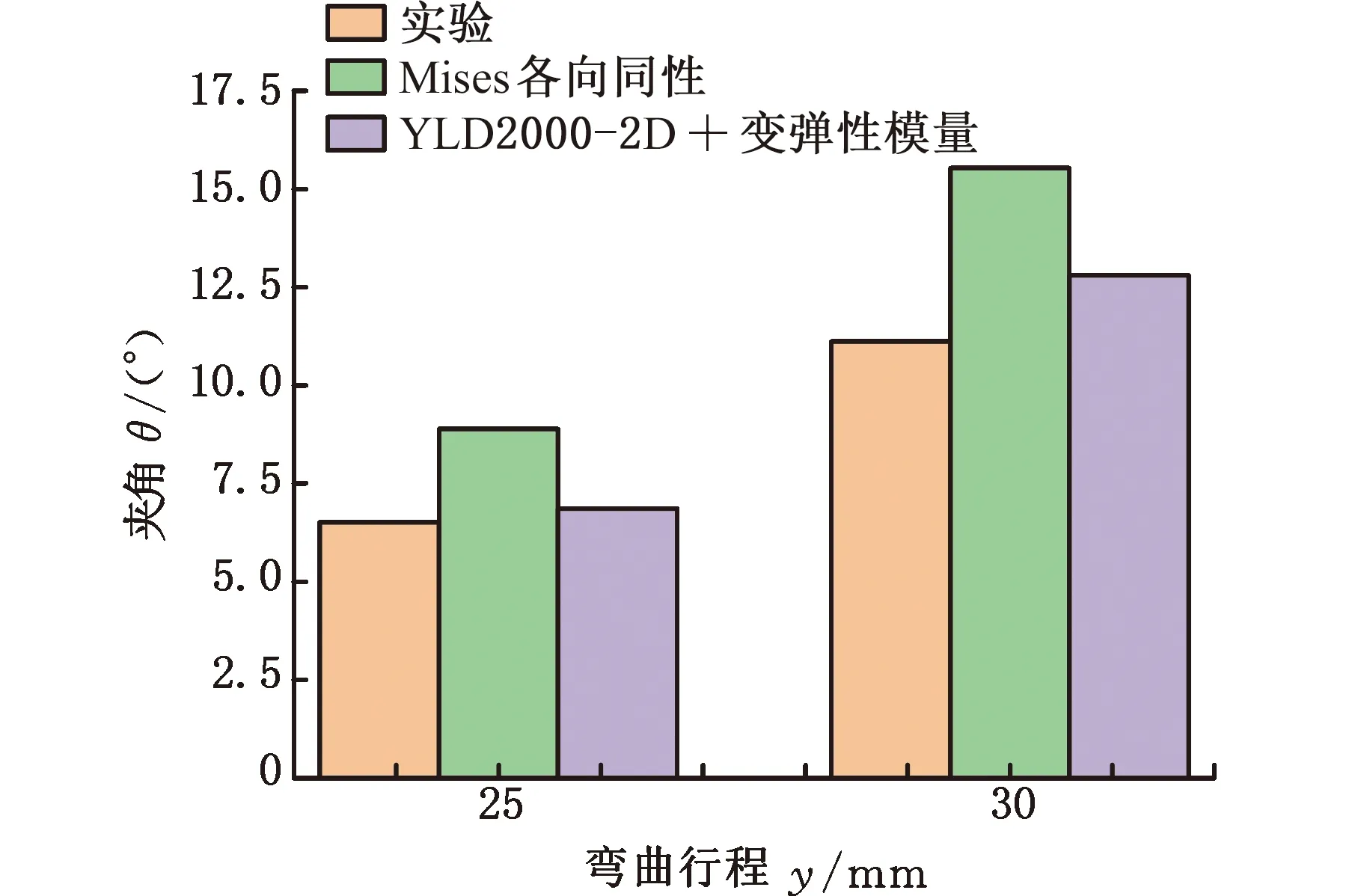
图15 不同本构模型在25 mm、30 mm弯曲行程下回弹预测的差异Fig.15 Difference of springback prediction of different constitutive models under 25 mm and 30 mm bending stroke
4 结论
(1)Ti-6Al-4V钛合金的屈服强度及弹性模量在RD、DD、TD三个方向上存在明显的各向异性。
(2)Ti-6Al-4V钛合金弹性模量随塑性应变增加而减小,最终变为一个定值。基于以上规律,建立了Ti-6Al-4V钛合金变弹性模量数学模型。
(3)基于YLD2000-2D屈服准则及变弹性模量模型,建立了Ti-6Al-4V钛合金本构模型,并通过Umat二次开发接口,将其嵌入ABAQUS软件中进行Ti-6Al-4V钛合金板材五点弯曲回弹数值模拟。
(4)基于YLD2000-2D屈服准则及变弹性模量的本构模型显著提高了Ti-6Al-4V钛合金板材五点弯曲回弹预测精度,相比Mises各向同性本构模型最高提高了31.18%。
