形如2m(m+1)的Fibonacci数仅有0和144

张少男，杨 鹏

（辽宁科技大学 理学院，辽宁 鞍山 114051）

关于整数数列，特别是Fibonacci数列Fn+2=Fn+1+Fn，F0=0，F1=1及其伴随序列Lucas数列Ln+2=Ln+1+Ln，L0=2，L1=1的形数问题，数论学家们做了大量的讨论与研究。

1963年，Rollett［1］提出Fibonacci数中除F0、F1、F2、F12以外，是否存在其他的平方数的问题。1964年，Cohn［2］用递归数列方法考察Fibonacci数和Lucas数列的性质，求得其中形如平方数或二倍于平方数的整数。1965年，柯召［3］利用不定方程解决了Fibonacci数列中的平方数问题。1981年，Lagarias［4］解决了其中的立方数m3问题。

由于递归方法的局限性，Luo［5-9］在此基础上作了进一步的改进，利用构建雅可比符号恒等式的方法，解决了Fibonacci数和Lucas数中的三角形数m(m+1)/2问题。随后，罗明又解决了其中的殆平方数m(m+1)和五角形数问题［7］。1996年，Mcdaniel［10］使用罗明的方法解决了Pell数列Pn+2=2Pn+1+Pn，P0=0，P1=1中的三角形数问题。2001～2005年，Prasas等解决了Fibonacci数和Lucas数中的七角形数问题，以及Pell数列及其伴随数列中的五角形数和七角形数等问题［11-17］。

本文首先给出一些已知的Fibonacci数和雅可比符号的简单结果，并以此推广罗明建立的关于Fibonacci数和Lucas数的雅可比准则。之后，通过新建立的恒等式，结合Mathematica筛选，最终求得所有可表为4倍三角形数的Fibonacci数。

1 一些Fibonacci数及雅可比符号的简单结果

Lucas数列作为Fibonacci数的伴随序列，两者有如下等式成立

当n是一个正整数时，若n≡±2(mod 6)，有

对于雅可比符号，设m,n为大于1的奇数，有以下式子成立

对任意正整数m，Fibonacci数关于modm的剩余类序列具有周期性［18］，部分结果如表1所示。

表1 F n关于部分模m的剩余类周期Tab.1 Period of F n(mod m)

2 主要定理

引理1如果n为整数且满足n≡±2(mod 6)，有

证明：由于n≡±2(mod 6)，考虑Fn，Ln关于部分模m的剩余类周期性，有Ln≡3(mod 4)，Fn≡1(mod 2)，2n≡±4(mod 12)，从而有L2n≡7(mod 8)，因此

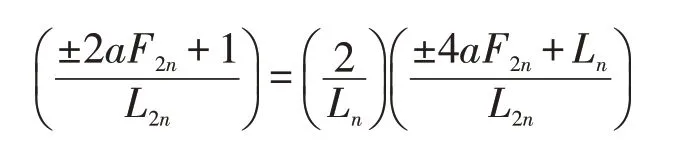
由公式（10），有

由公式（11），有

再由公式（6），有

由公式（12），有

因此

由公式（6）和公式（10），得到

又由公式（4），有

若Fn≡1(mod 4)，有

若Fn≡1(mod 3)，有

因此总有

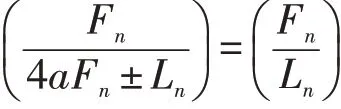
又因为

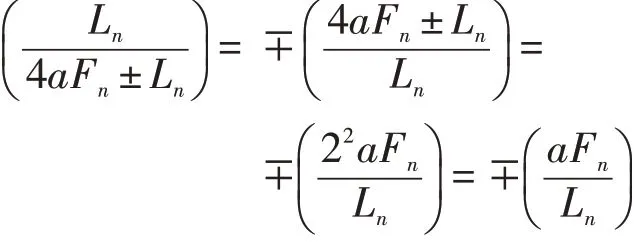
得到

特别地，当时a=1，有

当a为偶数时，即是文献［5］中的引理1。

很显然，当Fn具有形式2m(m+1)时，2Fn+1是一个大于1的平方数。所以，只需找到所有使得2Fn+1为平方数的n即可。

引理2当n≡0(mod 160)时，2Fn+1为一个平方数，当且仅当n=0。

证明：若n≠0，可令m=8，n=2×5×2m×k。

由公式（8），有Fn=-F2m(modL2m)，所以

由引理1，有

对序列{4Fm-Lm}取模21，得到剩余类周期为16。

因为当m=8时，4Fm-Lm≡16(mod 21)，所以

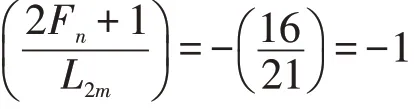
故而2Fn+1不可能为一个平方数。

当n=0时，2F0+1=1=12。证毕。

引理3当n≡12(mod 800)时，2Fn+1为一个平方数，当且仅当n=12。

证明：如果n≠12，则可令n=12+2r×2×2×25×k，其中r≥3,2∤k。

取m=2r，从而m≡8,16,24,32(mod 40)，同时有2m≡16,32,48,64(mod 80)。

由公式（8），有

从而

对序列{L2m}取模287，所得剩余类具有周期80。当2m≡16,64(mod 80)时，L2m≡198(mod 287)；当2m≡32,48(mod 80)时，L2m≡170(mod 287)。

由以上两个引理能得到以下推论。

推论1若n≡0,12(mod 800)，则2Fn+1是一个平方数，当且仅当n=0,12。

下面证明最后一个引理。

引理4若n≢0,12(mod 800)，则2Fn+1不可能为一个平方数。

证明：采用对2Fn+1取模的方式，应用Mathematica软件计算来证明。

mod 11。{2Fn+1}的剩余类周期为10。当n≡6,8(mod 10)时，{2Fn+1}为mod 11的平方非剩余，故可排除。

mod 5。{2Fn+1}的剩余类周期为20。当n≡1,2,4,6,7,8,13,19(mod 20)时，{2Fn+1}为mod 5的平方非剩余，故可排除。

mod 3。{2Fn+1}的剩余类周期为8。当n≡3,5,6(mod 8)时，{2Fn+1}为mod 3的平方非剩余，故可排除。剩n≡0,9,10,11,12,15,17,20,23,25,31,32,34(mod 40)。

mod 41。{2Fn+1}的剩余类周期为40。当n≡9,10,11,17,23,31,34(mod 40)时，{2Fn+1}为mod 41的平方非剩余，故可排除。剩n≡0,12,15,20,25,32(mod 40)。

mod 101。{2Fn+1}的剩余类周期为50。当n≡20,25,40,52,55,60,72,92,95,105,120,140,145,152,160,172,175,192(mod 200)时，{2Fn+1}为mod 101的平方非剩余，故可排除。

mod 151。{2Fn+1}的剩余类周期为50。当n≡15,65,80,135,180,185(mod 200)时，{2Fn+1}为mod 151的平方非剩余，故可排除。剩n≡0,12,32,100,112,132(mod 200)。

mod 401。{2Fn+1}的剩余类周期为200。当n≡32,132(mod 200)时，{2Fn+1}为mod 401的平方非剩余，故可排除。剩n≡0,12(mod 100)。

mod 2161。{2Fn+1}的剩余类周期为80。当n≡72(mod 80)时，{2Fn+1}为mod 2161的平方非剩余，故可排除。

mod 3041。{2Fn+1}的剩余类周期为160。当n≡32,40,52,60,112,120(mod 160)时，{2Fn+1}为mod 3041的平方非剩余，故可排除。

mod 1601。{2Fn+1}的剩余类周期为160。当n≡92,100,132,140(mod 160)时，{2Fn+1}为mod 1601的平方非剩余，故可排除。

剩下n≡0,12,400,500(mod 800)。

对于n≡400(mod 800)，它包含于n≡16(mod 32)中，这一情形可分为n≡16,48(mod 64)，进而可分为n≡16,48,80,112,144,176(mod 192)。

mod 769。{2Fn+1}的剩余类周期为192。当n≡16,48,80,112,176(mod 192)时，{2Fn+1}为mod 769的平方非剩余，故可排除。

mod 3167。{2Fn+1}的剩余类周期为192。当n≡144(mod 192)时，{2Fn+1}为mod 3167的平方非剩余，故可排除。这样完全排除n≡400(mod 800)。

对于n≡500(mod 800)，Fn≡±F20(modL80)，而，故而排除n≡500(mod 800)。

最终只剩下n≡0,12(mod 800)。证毕。

定理1形如2m(m+1)的Fibonacci数仅有F0和F12。

证明：综合推论1和引理4，可知定理1成立。

3 结论

本文改进了罗明解决Fibonacci数为三角形数问题的方法，并以此考虑Fibonacci数为三角形数的倍数问题，得到Fibonacci数中仅0和144是三角形数的四倍。本文所使用的雅可比符号恒等式也可用来求解Fibonacci数中的三角形数或殆平方数，但对于解决更一般的情况，如Fibonacci数为形数或形数的倍数问题还需进一步研究。