基于海温因子的传递函数模型在黄海绿潮规模预测中的应用

刘旭，梁颖祺，王兆毅，李志杰，王峥，季轩梁，何恩业

（1.国家海洋环境预报中心，北京 100081；2.北京林业大学经济管理学院，北京 100083）

1 引言

自2007 年首次在青岛监测到浒苔规模性聚集形成绿潮以来[1-2]，浒苔灾害已经连续10余年在黄海周期性爆发。大量浒苔堆积在近岸海域，给海洋生态环境造成严重威胁[3-4]。研究表明海表面温度（Sea Surface Temperature，SST）是影响浒苔生长和死亡的主要生态因子[5-6]。通过实验室设置温度梯度可以分析浒苔对温度的敏感性，吴洪喜等[7]认为浒苔适宜生长的海水温度为10～30 ℃，在缺乏阳光的干露状态下可承受的最高温度为38 ℃。Taylor等[8]认为浒苔适宜生长的温度范围为10～25 ℃，最高生长率温度范围为15～20℃，最适萌发温度为20 ℃。韩红宾等[5]认为浒苔孢子/配子萌发适宜温度为15～25 ℃，最适萌发温度为20 ℃；浒苔孢子/配子放散的温度为20～30 ℃，最适宜放散温度为25 ℃。忻丁豪等[9]认为20～26 ℃是浒苔生长发育的最佳水温，此温度区间下当盐度为26～32 时生长率可达到36%以上[10]。陈月红[11]发现浒苔在25℃组和30℃组中，相对增长率下降趋势明显，说明浒苔不具有耐高温性[5]，高SST极大地抑制了浒苔的生长。

上述研究均表明SST 是浒苔生长的重要限制因子，但不同学者通过对照培养实验获取的浒苔最适生长温度范围具有明显差异性。黄海浒苔爆发是自然海域多种环境因子共同影响的过程[12]，因此实验室模拟浒苔生长环境存在一定局限性[13]。在实证研究方面，李弘毅[13]基于时间序列的GOCI（Geostationary Ocean Color Imager）影像定性分析了2011—2017年浒苔爆发的环境驱动因素，得出5—7 月SST 都处于浒苔最适宜生长的温度范围内。张广宗等[14]基于环境卫星HJ-1A/1B 的CCD（Change-Coupled Device）影像和MODIS（MODerate Resolution Imaging Spectroradiometer）影像对2011—2017年南黄海海域浒苔信息进行了提取，结合ESRL（Earth System Research Laboratroy）海温数据对浒苔生长进行了定性分析，结果表明每年5—8 月SST逐月升高为浒苔生消过程提供了环境条件。辛蕾等[15]和刘旭等[16]基于多源卫星数据将浒苔生命周期分为发生—发展—爆发—衰落—消亡5 个阶段，并定性分析了绿潮覆盖面积随表层水温的变化呈现出先上升后下降的趋势，指出约在22 ℃时覆盖面积达到最大值。何恩业等[17]在构建黄海浒苔漂移输运模型时耦合了生长消亡过程的生态模块，将海温因素耦合到黄海浒苔的生长率公式中，设置最适宜温度区间为15～20 ℃，生长率为1.15～1.80，临界死亡温度为25 ℃，最大死亡率为1.10。对于绿潮和海温的关系，尽管学者在室内培养实验和生态动力学模型等方面开展了定量研究，但目前基于遥感影像资料的实证研究仍处在定性分析阶段，定量化研究鲜有报道。为给绿潮灾害规模预测提供借鉴，本文基于2010—2019 年多源卫星遥感黄海绿潮资料，分析了绿潮覆盖面积与SST 间的协整关系和Granger 因果关系，使用协整模型和传递函数模型对绿潮灾害爆发条件下的规模变化过程进行模拟和预测。2018—2019 年绿潮覆盖面积的预测检验可验证该方法的适用性和可靠性。在浒苔的生消机制尚不完全清晰的背景下，基于数据驱动的时间序列法可有效提取历史信息，为绿潮预测提供技术支持，为深入挖掘绿潮的生态影响因素提供参考。

2 数据与方法

2.1 数据来源

黄海绿潮覆盖面积数据资料来源于2010—2019年国家卫星海洋应用中心的每日业务化绿潮遥感影像解译结果，其中2010—2018年的反演结果主要基于MODIS 和HY-1B 数据，2019 年反演结果主要基于MODIS和HY-1C数据，MODIS和HY-1B分辨率为250 m，HY-1C 分辨率为50 m。表层海温数据来源于日本气象厅（Japan Meteorological Agency，JMA）发布的近实时的日变化表层海温数据（Merged satellite and in-situ data Global Daily Sea Surface Temperature，MGDSST，网址：http://ds.data.jma.go.jp/gmd/goos/data/pub/JMA-product/）。该数据融合了AVHRR（Advanced Very High Resolution Radiometer）卫星红外传感器数据、WindSat、AWSRE和AWSR-2 微波传感器数据以及来自浮标和船测现场的全球SST 产品，水平分辨率为0.25°，时间分辨率为1 d，其资料已被广泛应用于海洋科学研究[18]。

由于绿潮遥感受云层遮挡影响较大，难以获得成像条件较好的日数据，因此，按照每年绿潮生消的起止规律，将研究周期设定为每年的5 月8 日—8月7 日[19]，挑选出成像条件较好的反演结果，按照每月1—7 日，8—14 日，15—21 日，22 日—月底进行周平均，形成绿潮遥感覆盖面积周平均时间序列{yt}。根据当日浒苔覆盖区域的经纬度范围解析对应区域内的日均海温数据，按照绿潮覆盖面积周平均序列的处理方法，合成相应的SST周平均时间序列{xt}。

将2010—2017 年数据作为实验集用于模型模拟，2018—2019 年数据作为测试集用于模型预测检验，以此评估模型预测精度。

2.2 研究方法

2.2.1 Granger 因果检验

采用Granger 因果检验，从统计角度识别自变量海温序列{xt}是否为因变量绿潮遥感覆盖面积序列{yt}的原因，即SST 变化是否对绿潮覆盖面积变化有显著影响。假设{xt}和{yt}是宽平稳序列，至少存在一个h= 1,2…使得式（1）成立，说明{xt}序列历史信息的加入能提高{yt}的预测精度，则称xt是yt的原因[20]。

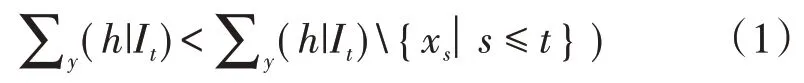
式中，It表示在t时刻及以前的所有信息集合。设yt(h|It)为信息It可获得的h步最小均方误差预测，则相应的均方预测误差记为∑y(h|It)，It{xs│s≤t}为除开变量xs在t时刻及以前的信息。

原假设{xt}不是{yt}的Granger 原因，备择假设{xt}是{yt}的Granger原因。

在备择假设成立的条件下，构造F统计量：

式中，SSEr为有约束条件下的随机波动，SSEu为无约束条件下的残差平方和；q为{xt}序列的历史延迟阶数；n为序列长度；p为{yt}的自回归阶数。当F统计量大于F1-α(q,n-q-p- 1)时，拒绝原假设，认为{xt}是{yt}的Granger原因。

2.2.2 协整模型

协整模型可以有效地衡量序列之间是否具有长期相关性。假定海温时间序列为自变量{xt}，绿潮覆盖面积序列为因变量{yt}，构造回归模型：

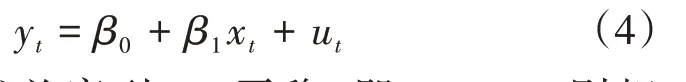
如果回归残差序列{ut}平稳，即ϵt～I(0)，则相应变量序列{yt}与自变量序列{xt}之间具有协整关系。检验双变量协整关系时，需满足xt～I(d)且yt～I(d)。在建模时首先需要检验数据的平稳性以确定序列是否符合建模要求。当变量均为d阶单整时，采用EG 检验法对回归残差进行ADF（Augmented Dickey Fuller）平稳性检验，假设条件为：

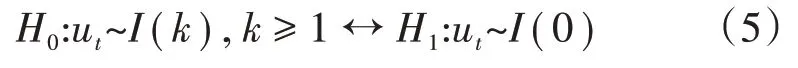
由于{ϵt}序列是回归模型式（4）中最小二乘法估计的残差，ADF 检验法的统计量极限分布与观测样本有所不同，因此需采用专门用于协整关系的ADF-t检验临界值表判断{ϵt}是否存在单位根及协整关系[20]。

当式（4）中回归残差序列{ut}不平稳时，说明蕴含着历史信息之间的相关性，可以进一步构建{ϵt}的自回归滑动平均模型（Auto-Regressive and Moving Average model，ARMA）。协整模型可表示为：

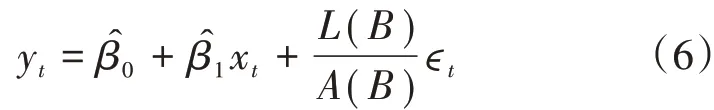
式中，L(B)为{ϵt}q阶移动平均系数多项式；A(B)为{ϵt}p阶自回归系数多项式；ϵt为白噪声序列，ϵt～N(0,σ2)。

2.2.3 传递函数

建立海温序列{xt}作为输入变量绿潮覆盖面积序列{yt}的单输出传递函数模型：

式中，Ω(B)、E(B)、Θ(B)和Ф(B)为滞后算子B的多项式，其阶数依次为s、r、q和p；b为延迟参数，即xt的b期滞后值才开始对yt产生影响；εt为随机干扰性，满足εt～iidN(0,σ2)，其与xt相互独立；为传递函数，可表示为V(B)。

3 结果与讨论

3.1 黄海浒苔爆发期间覆盖面积和SST变化规律

2010—2019 年我国黄海绿潮爆发期内浒苔覆盖面积的时间序列图呈现出明显的以年为周期的季节性单峰波动规律（见图1a）。除2010 年和2015年在第8期（7月上旬）达到峰值外，其余年份均在第6 期和第7 期（6 月中下旬）达到峰值，绿潮最大覆盖面积范围为330～905 km2，峰值平均为576 km2，峰值中位数为654 km2。 图2a 中自相关函数（AutoCorrelation Function，ACF）也显示了绿潮爆发的循环特性，绿潮覆盖面积ACF序列以12期为一个周期，第24 期和第36 期均有明显的正峰值，第6 期表现出最大负相关性，说明绿潮覆盖面积变化总体规律为1～6期是由初始值逐渐增长到峰值的阶段，6～12 期是由峰值逐渐到消亡的阶段，这与图1a 反映出的绿潮覆盖面积年变化规律基本一致。

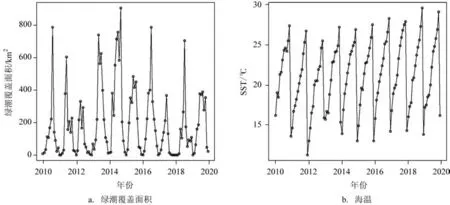
图1 时间序列图Fig.1 Time Series Diagram

图1b显示，2010—2019年绿潮爆发区域海温变化呈年周期的季节性增长，SST 范围为11.2～29.5 ℃，初始温度区间为11.2～15.8 ℃，平均温度为13.8 ℃。2012 年为初始温度最低值，当年绿潮峰值规模为10 a 间最小值，2014 年为初始阶段温度最高值，当年绿潮规模为10 a 间最大值。根据ACF 统计结果（见图2b），将第6 期设定为每年绿潮爆发的峰值期，峰值阶段海温区间为19.1～21.5 ℃，平均温度为20.7 ℃；最终消亡阶段（第12期）海温区间为25.4～29.5 ℃，平均温度为27.5 ℃。统计结果表明，浒苔从生长到消亡的SST 区间为11.2～29.5 ℃，与吴洪喜等[7]的实验室海温梯度（10～30 ℃）对浒苔生长产生影响的分析结果基本一致。萌发温度（第1期）有7 a 低于文献中浒苔微观繁殖体的最适宜萌发温度15 ℃[5]，也低于陈月红[11]采用硝酸还原酶活力（Nitric Acid Reductase Activity，NRA）指标测定的浒苔的NRA平均值15 ℃。浒苔快速增长期（4～6 期）的温度区间变化范围为16.4～21.5 ℃，与白雨等[19]的实证研究结果较为一致，比Taylor 等[8]和Cui 等[21]的实验室研究成果（15～20 ℃）整体偏高1.5 ℃，在韩红宾等[5]通过实验测定的浒苔孢子/配子适宜萌发温度15～25 ℃范围内。绿潮出现的最后位置区域（第12 期）的SST 平均达到27.5 ℃，与韩红宾等[5]认为的浒苔孢子/配子放散的温度为20～30 ℃结论一致，较白雨等[19]实证研究成果偏高1.5℃，与陈月红[11]梯度水温在25 ℃组和30 ℃组时浒苔相对生长率下降明显的结论相一致。

由图3可见，绿潮覆盖面积对不同滞后期（Lag）的SST 序列的互相关系数（Cross-Correlation Function，CCF）存在明显的正弦曲线波动规律，CCF 超过蓝色虚线表明两序列具有显著相关性。Lag=-2 时存在明显峰值（CCF=0.48），说明SST 序列领先绿潮覆盖面积序列2 期；Lag=5 时也存在明显峰值（CCF=-0.46），说明SST 序列还存在滞后绿潮覆盖面积序列5 期的规律，CCF 由正转负意味着初期SST 与绿潮覆盖面积为同方向变化，5 期后反方向变化趋势最为明显。

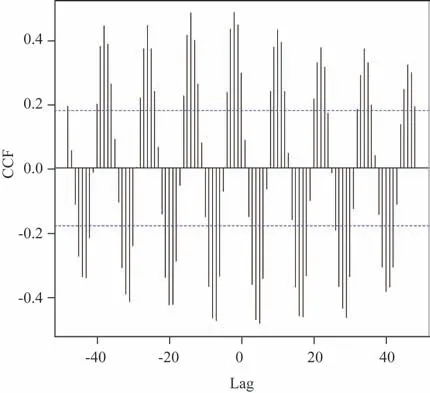
图3 绿潮覆盖面积与海温互相关系数图Fig.3 Correlation coefficient between green tide coverage area and SST

时间序列图（见图1）和自相关函数图（见图2）均表明两序列具有明显的季节周期（s=12），因此分别采用wold 分解法（见图4）和季节差分法（见图5）消除季节效应。通过wold 分解法提取确定性周期变化规律，将原序列每期值分别减去每期的平均值来消除序列的季节性，新生成序列分别记为{area_st}和{temp_st}。季节差分法是将每期值减去上一年对应期数据的差，新生成序列分别记为{area_dt}和{temp_dt}。

图2 自相关函数和偏自相关函数图Fig.2 Autocorrelation function and partial autocorrelation function

图4 和图5 的时间序列结果表明两种方法均消除了原序列明显的季节波动规律。ACF 结果表明wold 分解海温序列呈现出缓慢下降的拖尾趋势（见图4a），偏 自 相 关 函 数（Partical AutoCorrelation Function，PACF）一阶截尾；绿潮覆盖面积的ACF 和PACF 均呈现出截尾特征（见图4b）。季节差分海温序列也呈现出拖尾特征（见图5a），并且仍具有正弦波动规律；绿潮覆盖面积的ACF 和PACF 均表现出在1 阶和12 阶显著（见图5b），呈一定的季节波动特征。总体来看，wold 分解法去季节周期效果优于差分法，但从ACF 衰减速度来看季节差分后的序列更为平稳。

图4 wold分解法Fig.4 Wold decomposition method

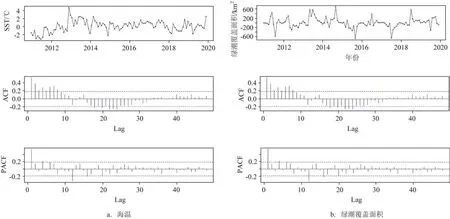
图5 季节差分法Fig.5 Seasonal difference method

3.2 平稳性检验与最优滞后阶数选取

为避免因数据出现“伪回归”而影响估计结果的有效性，我们首先需要对数据进行单位根平稳性检验和协整检验。综合采用ADF 检验法和PP（Philips & Perron）检验法，零假设均为序列为存在单位根的非平稳过程，备择假设为平稳序列，在5%的显著水平下拒绝存在单位根的原假设。结果表明（见表1），除海温原始序列{xt}外，其余序列在ADF 检验和PP 检验下均为无漂移项且无趋势的平稳序列。{xt}序列两种检验结果均为带漂移项的平稳序列，因此在以{xt}为自变量的回归方程中引入截距项。由于各序列为I（0）单整序列，原始序列、wold 分解法序列和季节差分序列之间必然具有长期相关性的协整关系。

表1 单位根检验结果Tab.1 Results of unit root test

自变量和因变量存在协整关系，进一步采用Granger 因果检验法诊断海温是否可作为绿潮覆盖面积模型的自变量，即检验海温是否可作为回归方程的自变量提高模型预测效果。Granger 检验对滞后阶数有较大的敏感性，选取自变量领先因变量0～5 期，原假设为海温不是绿潮覆盖面积变化的原因，在5%的显著水平下拒绝原假设。结果表明（见表2），原始序列在0～5阶均为Granger的统计原因，0阶{xt}是{yt}的Granger原因的概率为99.997%，说明海温当期的变化会引起绿潮覆盖面积的变化。去掉季节效应的序列自变量和因变量的Granger 因果检验均不能拒绝原假设，说明在模型构建时加入海温数据序列不能提高预测精度。

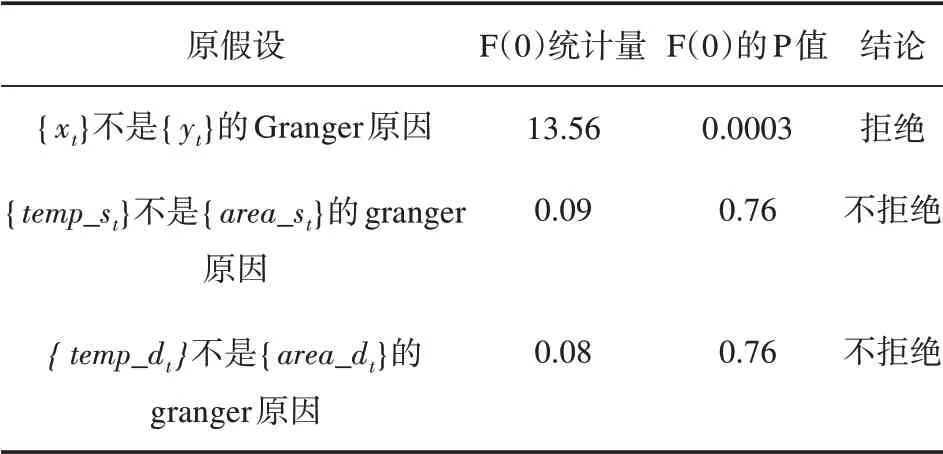
表2 Granger因果关系检验结果Tab.2 Granger causality test results

3.3 协整回归模型的建立和预测

根据平稳性检验结果，{xt}和{yt}均为0 阶单整，建立的以{xt}为单变量的回归模型残差也具有平稳性，符合协整模型建模要求[20]。采用EG两步法构建协整模型，通过最小二乘法构造回归模型为：

经过ADF 检验，式（8）回归残差序列{ut}为平稳非白噪声序列，说明两个变量间存在协整关系，但建立协整回归模型还需要进一步提取残差序列中的相关信息，因此，构建残差序列的ARMA 模型。根据{ut}的ACF 和PACF 的性质（见图6a），回归残差序列的ACF 为拖尾特征，PACF 为1 阶截尾特征，因此初步设定式（8）中的残差序列拟合模型为AR（1）。

采用最大似然法对模型参数进行估计，Box-Ljung 法判断模型残差为平稳非白噪声序列。重新进行模型定阶数、参数估计和残差检验后，构建残差模型阶数为ARMA（2，0，2），各参数C 均通过显著性检验（见表3），拟合后最终模型残差为平稳白噪声序列。模型可表示为：

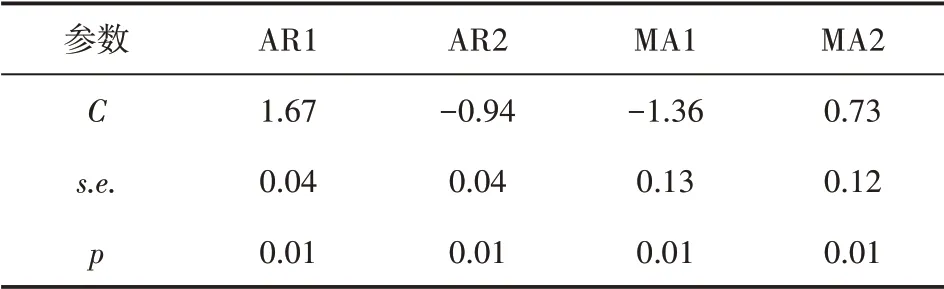
表3 协整模型残差参数显著性检验结果Tab.3 Significance test results of residual parameters of cointegration model

采用赤池信息准则（AIC）、校正的赤池信息准则（AICc）和贝叶斯准则（BIC）评价模型拟合精度（见表4）。协整模型拟合精度AIC=13.03，AICc=13.04，BIC=13.22。对2018—2019 年绿潮覆盖面积进行模型预测（见图6b），测试集为{yt}序列2018—2019年数据。图6b中黑色线为实际值（2010—2019年），红色线为拟合值（2010—2017 年）和预测值（2018—2019 年）。采用均方根误差（Root Mean Square Error，RMSE）和 平 均 绝 对 误 差（Mean Absolute Error，MAE）评价模型的预测精度（见表4）。协整模型的预测精度为MAE=122.48，RMSE=171.40。式（9）的计算结果表明，xt与yt相关性较强，海温与绿潮面积变化具有显著的正相关性。虽然在6期后绿潮面积有从峰值下降的趋势，但是6～12期海温（19.7～29.5 ℃）仍基本处于浒苔最佳生长范围内（10～30 ℃）[7]，仅第12 期平均温度大于25 ℃，因此式（8）中自变量系数表现为海温每升高1 ℃，绿潮覆盖面积增长15.07 km2。残差项表明除受海温影响外，绿潮覆盖面积还具有显著的自身变化规律，滞后因子B 表明绿潮规模短期变化是ARMA（2，0，2）的自回归平均移动过程，残差模型的系数表明{yt}t-1期对t期的影响大于t-2期的动态过程，t-1 期的AR 过程和t-2 期的MA 过程参数为负表明具有负向调节趋于平稳的作用，6～12 期由于t-1和t-2 期的{yt}较大，负向调节功能更为明显，表现为{yt}的下降趋势，即绿潮覆盖面积由峰值衰减的过程。

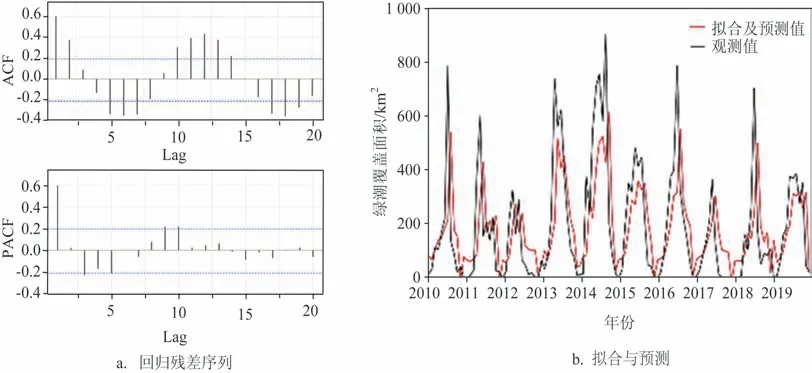
图6 协整模型Fig.6 Cointegration model

表4 协整模型和传递函数模型精度Tab.4 The precision of co-integration model and transfer function model

3.4 传递函数模型的建立和预测

以{xt}为输入变量，{yt}为输出变量构建动态回归过程的传递函数模型。首先对序列进行预白化处理，基于Box-Jenkins 建模方法对{xt}进行ARMA模型拟合，结果为带漂移项的ARMA（2，0，1）模型，传递函数模型参数通过显著性检验（见表5）和残差进行白噪声检验，预白化滤波器为：

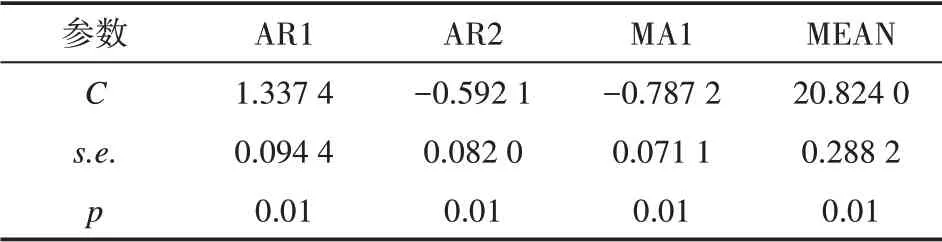
表5 预白化滤波器参数显著性检验结果Tab.5 Significance test results of pre-whitening filter parameters

根据预白化生成的{xt}残差序列{αt}和{yt}的派生序列{βt}计算互相关函数，排除自变量自相关干扰后两者仍具有强相关性，该结果与协整检验和因果检验结果保持一致，说明海温与绿潮覆盖面积变化的长期趋势具有强相关性。由于预白化过程去除了海温序列的自相关性，与图3 的滞后阶数不同，{αt}序列滞后2 期时达到最大值，式（10）中xt的滞后算子为0、B和B2，也表明滞后0～2期海温对绿潮覆盖面积有显著影响。将新生成的{αt}和{βt}进行回归，模型残差是平稳非白噪声序列，根据图7a将传递函数模型残差设定为ARMA（0，0，2），整个传递函数模型参数通过显著性检验（见表6），传递函数模型残差为平稳白噪声，传递函数模型函数可表示为：

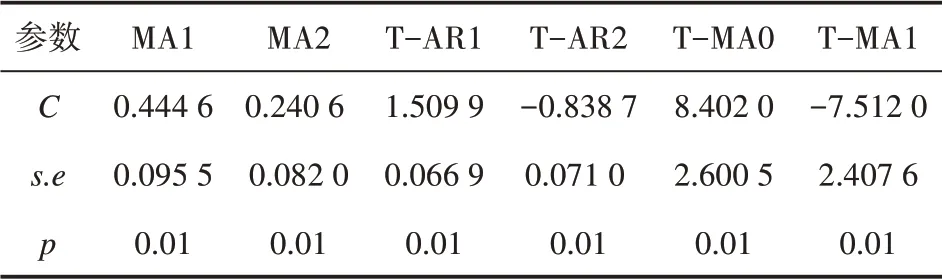
表6 传递函数模型参数显著性检验结果Tab.6 Significance test results of transfer function model parameters

模型拟合精度为AIC=5.40，AICc=5.41，BIC=5.53。对2018—2019 年的绿潮覆盖面积进行预测（见图7b），预测精度为RMSE=160.94，MAE=109.70。式（11）中xt的参数项表明，海温对绿潮覆盖面积的影响是显著的，表现为海温滞后的0～2期对绿潮覆盖面积规模的非线性动态关系，其中t 和t-1 期的MA 过程影响最为显著，t-2 期的AR 过程具有负向调节作用。误差项表明因变量yt除与自变量xt具有相关性外，还具有绿潮覆盖面积变化的自身时序关系，表现为在1～2 期的非线性平均移动回归过程中，增长阶段的yt残差的负向调节机制不明显，而峰值后t-1 期和t-2 期yt的负向调节更为显著，该结论与协整模型中yt的变化规律一致。

3.5 模型预测精准度评价

将海温序列进行自回归预白化处理，提升了模型的拟合精度，即便是对模型复杂性更具有惩罚性的BIC 准则，传递函数模型也优于协整模型。图6b和图7b 的拟合结果表明，从长期趋势来看，两个模型均模拟出2013年、2014年和2016年绿潮灾害较为严重，2012年和2017年绿潮灾害较轻。从年内模拟效果看，10 a间生消过程估计趋势与遥感反演结果趋势一致，传递函数模型在每年的生消过程中还可以模拟出更多的绿潮覆盖面积增减的信息。

传递函数模型预测的RMSE 与协整模型相比提高了6.1%，MAE 提高了10.4%。图6b 和图7b 的预测结果表明，两模型均预测出了2018年绿潮具有较大规模，2019 年绿潮规模处于平均水平，2019 年的传递函数模型预测与真实值非常接近，说明模型具有良好的预测能力。

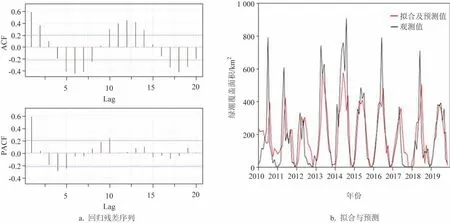
图7 传递函数模型Fig.7 Transfer function model

4 结论和展望

本文基于黄海绿潮遥感覆盖面积和表层海温数据开展ADF 检验和PP 检验，结果显示两变量均为0 阶单整非白噪声序列，两变量间具有长期协整性。绿潮覆盖面积自相关系数变化规律表明面积峰值集中在6 月中下旬出现，海温与绿潮覆盖的相关系数波动规律表明两者具有先正相关后负相关的季节特征。分别采用wold 分解法和季节差分法消除序列中年度波动因素，进一步采用Granger 因果检验法发现，原始海温序列在领先0～5阶均具有显著互相关性，说明海温可作为绿潮覆盖面积变化模型的自变量因子，消除季节波动的两类序列间存在长期协整性但海温不能作为绿潮覆盖面积变化模型的自变量因子。利用协整模型和传递函数模型，采用海温因子构建静态回归模型和动态回归模型，模型参数的显著性和残差检验说明两模型均具有可预测性。综合采用赤池信息准则和贝叶斯准则评价拟合效果，结果表明传递函数模型整体优于协整模型。根据均方根误差和平均绝对误差比较模型预测效果，传递函数模型预测精度比协整模型的RMSE 提升了6.1%，MAE 提升了10.4%。此外，传递函数参数表明可以利用本周及滞后1～2 周的海温数据预测本周的绿潮覆盖面积变化，增强了预测的时效性，因此传递函数模型是海温和绿潮生消变化更适合的预测模型。

绿潮灾害涉及多种环境因子共同作用，其爆发机制尚未十分清晰，当前从海洋物理、化学和生态层面预测浒苔绿潮的生态扩展和消亡过程尚有难度。时间序列方法不要求机制明确，可直接基于历史数据进行绿潮生消模拟和预测，还具有计算量低和业务性强的特点。本文以海温因子对浒苔生消变化的影响为研究切入点，得到基于主导因子的绿潮规模协整模型和传递函数预测方法，可作为绿潮年度预测的有效途径。为提高模型预测精准度，下一步还需将光照、营养盐和降水等其他生态因子纳入模型，并将时间序列模型嵌入漂移扩散预报系统，实现绿潮漂移趋势和规模变动预测，以应对防灾减灾的迫切需要。

致谢：感谢国家卫星海洋应用中心为本研究提供了宝贵的基础观测资料。