基于改进Informed-RRT* 算法的机器人路径规划

代军，李志明，李艳琴，赵俊伟

（河南理工大学 机械与动力工程学院，河南 焦作 454000）

0 引 言

近年来，移动机器人相关技术研究取得了较大突破，广泛应用于消防救援、医疗服务、餐饮服务、病毒消杀等领域。市场对移动机器人路径规划的精度和效率要求也逐步提高，路径规划技术作为移动机器人领域的核心技术之一，已成为科研人员关注的热点。

传统的路径规划算法包括蚁群算法［1］、遗传算法［2］、深度学习算法［3-4］、Dijkstra算法［5］、A*算法［6］等。T.Lung等［7］基于随机采样原理提出了Rapid-exploring Random Tree（RRT）算法，RRT算法在空间中随机提取采样点进行搜索，不需构建显式的任务空间，因而计算简单，且其具有概率完备性，即在规划中一定有解。户望力［8］针对RRT算法盲目采样的缺点，通过约束采样方向使节点树向目标点生长；李洋等［9］提出一种通过自适应采样步长使节点树快速覆盖采样区域的RRT算法；为解决RRT算法的路径非最优问题，S.Karaman等［10］提出RRT*算法，RRT*算法在规划过程中对新节点进行局部的剪枝重新布线，使路径接近最优解；刘猛等［11］将RRT*算法与三次曲线规划相结合，通过三次曲线规划使路径趋向平滑，减少汽车自主泊车时的横向移动；曹凯等［12］将人工势场法与RRT*算法融合，并通过人工势场引导节点树向目标方向生长；其他算法也相继被提出，如基于D*的Field D*［13］，基于RRT*的Informed-RRT*［14-15］等算法。

Informed-RRT*算法不需要构建显式的采样空间，但路径规划目的性差、路径优化效率低。为此，本文提出一种改进的Informed-RRT*路径规划算法。首先，在路径规划过程中引入贪心算法思想，当找到一个可以加入节点树的新采样点后，判断该节点能否直接与目标点连线，若条件成立，则结束路径规划过程进入路径优化过程，否则，继续采样；其次，将路径优化过程中搜索潜在最优父节点的搜索对象由构建的节点树替换为路径，减少路径优化过程中搜索潜在最优父节点时消耗的时间。通过融合两种优化方案，进一步提高路径规划的效率。

1 RRT*算法

RRT算法从起点开始，在空间中随机采样，并从路径树上找到与采样点最接近且能与它无障碍连接的父节点，然后连接父节点与采样点，将采样点加入路径树，直至终点附近区域被搜索到。RRT*算法在RRT算法的基础上重选父节点和剪枝重布线。首先，当采样点Xnew加入节点树后，以采样点为圆心画一个小圈，考虑在圈内是否有更好的父节点使起点到该节点的距离更短。若存在更加合适的父节点，就将它们连接起来，并去除原来的连线。然后，判断在圈内是否存在某种节点，该节点经过Xnew节点到初始节点的代价比该节点到初始节点原路径的代价小，若存在该类型节点，则将Xnew节点作为该节点的父节点，并断开该节点与原父节点的连接。

RRT*算法的伪代码如图1所示，M为实验地图，T为节点树，V为节点树的节点，E为节点树中节点之间的连线。图2（a）对应图1第4行，RRT*算法在图中采样得到节点Xrand。图1（第5-6行）Xrand节点在节点树中找到距离最近的节点Xnear（图2（a）中为Xnew），若Xrand节点与Xnear 节点的距离小于StepSize，Xrand节点即为Xnew节点。若Xrand节点与Xnear节点的距离大于StepSize，则依据步长StepSize，沿Xnear到Xrand方向上的截取一段等于Step Size的距离得到一个新的Xnew节点。图2（b）对应图1第7-8行，以Xnew为圆心，StepSize为半径画圆，在圆内搜索节点树中的潜在最优父节点，并保存到Ls之中。然后在Ls列表中找到Xmin节点，该节点保证从Xinit到Xmin到Xnew节点代价最小。图2（c），（d）对应图1第9～12行将Xnew节点与Xmin的关系加入到节点树中，然后根据Ls列表进行剪枝重布线，该过程首先检查Ls中每个节点x，如果从Xinit到Xnew到x的成本小于原来从Xinit到x的成本，并且可以将Xnew和x相连，则断开x和原来父节点的连接，将Xnew作为x的父节点连接到树中，并发布新的节点树T。图1（第13行）检测是否到达目标点。

图1 RRT*算法伪代码Fig.1 RRT*algorithm pseudocode

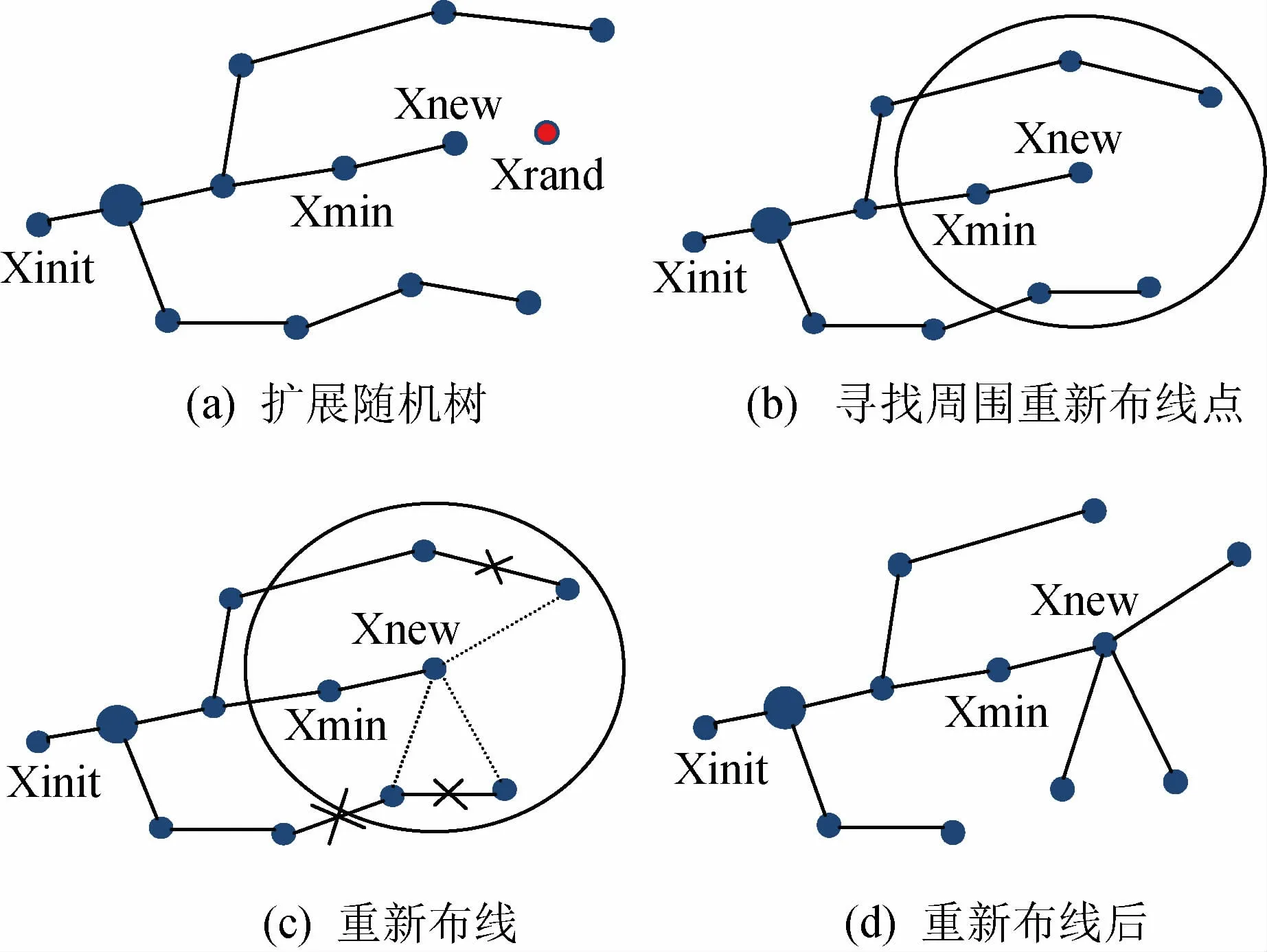
图2 RRT*算法重选父节点和重布线示意图Fig.2 RRT*algorithm reselect parent node and rewiring schematic diagram

2 Informed-RRT*算法

Informed-RRT*算法在RRT*算法基础上对采样空间进行优化，伪代码如图3所示。图3中，Cmin为起点到终点的距离，Cbest为规划路径的长度，初始化状态下Cbest为0。如图4所示，当得到第一条路径后，计算路径的长度Cbest，如式（1）～（2）所示，Cbest为椭圆两个顶点的距离2×a，Cmin为椭圆两个焦点的距离2×c。Informed-RRT*算法根据Cbest和Cmin两个参数，得到一个椭圆的采样空间。

图3 Informed-RRT*算法伪代码Fig.3 Informed-RRT*algorithm pseudo-code

图4 Informed-RRT*采样区域示意图Fig.4 Schematic diagram of the Informed-RRT*sampling area

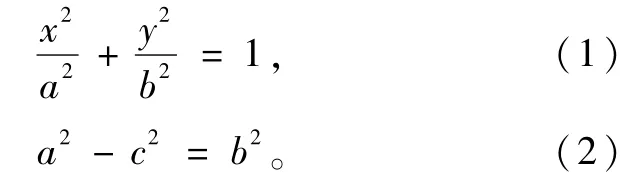
图3第3行中，Informed-RRT*算法在路径优化过程中的采样空间为椭圆区域，而RRT*算法的采样空间为整个区域，因此，Informed-RRT*算法随着路径不断被优化，Cbest不断缩短，采样空间会不断缩小，收敛速度不断加快。

3 Informed-RRT*算法的优化

Informed-RRT*算法以当前节点到目标点距离的阈值判断是否与目标点连线，然后结束路径规划进入路径优化过程。实际环境中，存在虽然与目标点的距离大于阈值但仍然可以直接与目标点连线的新采样点，面对此种情况，Informed-RRT*路径规划算法会继续采样，直到小于阈值的采样节点出现时才进入路径优化过程。相对而言，贪心算法会直接将新采样点与目标点连线，然后结束路径规划进入路径优化过程。除此之外，Informed-RRT*算法在路径优化过程中，搜索潜在最优父节点时的搜索对象是整个节点树，搜索过程中会消耗大量时间，严重影响路径规划效率。

3.1 贪心算法的引入

贪心算法以当前情况为基础，根据某个优化目的做最优选择，不考虑各种可能的整体情况，因此省去了为寻找最优解必须耗费的大量时间。

图5对应图6第13行，节点Goal为目标点，节点New_node为新得到的采样点，Dalte为节点搜索障碍物的搜索半径，Dis为采样点到目标点的距离。如图5（a）所示，原算法判断找到目标点的依据为：New_node与目标点的距离Dis小于Dalte。规划出第一条路径后，算法结束路径规划过程，进入路径优化过程。如图5（b）所示，引入贪心算法的改进Informed-RRT*算法判断是否找到目标点的依据为：新节点New_node能否直接与目标点连线。

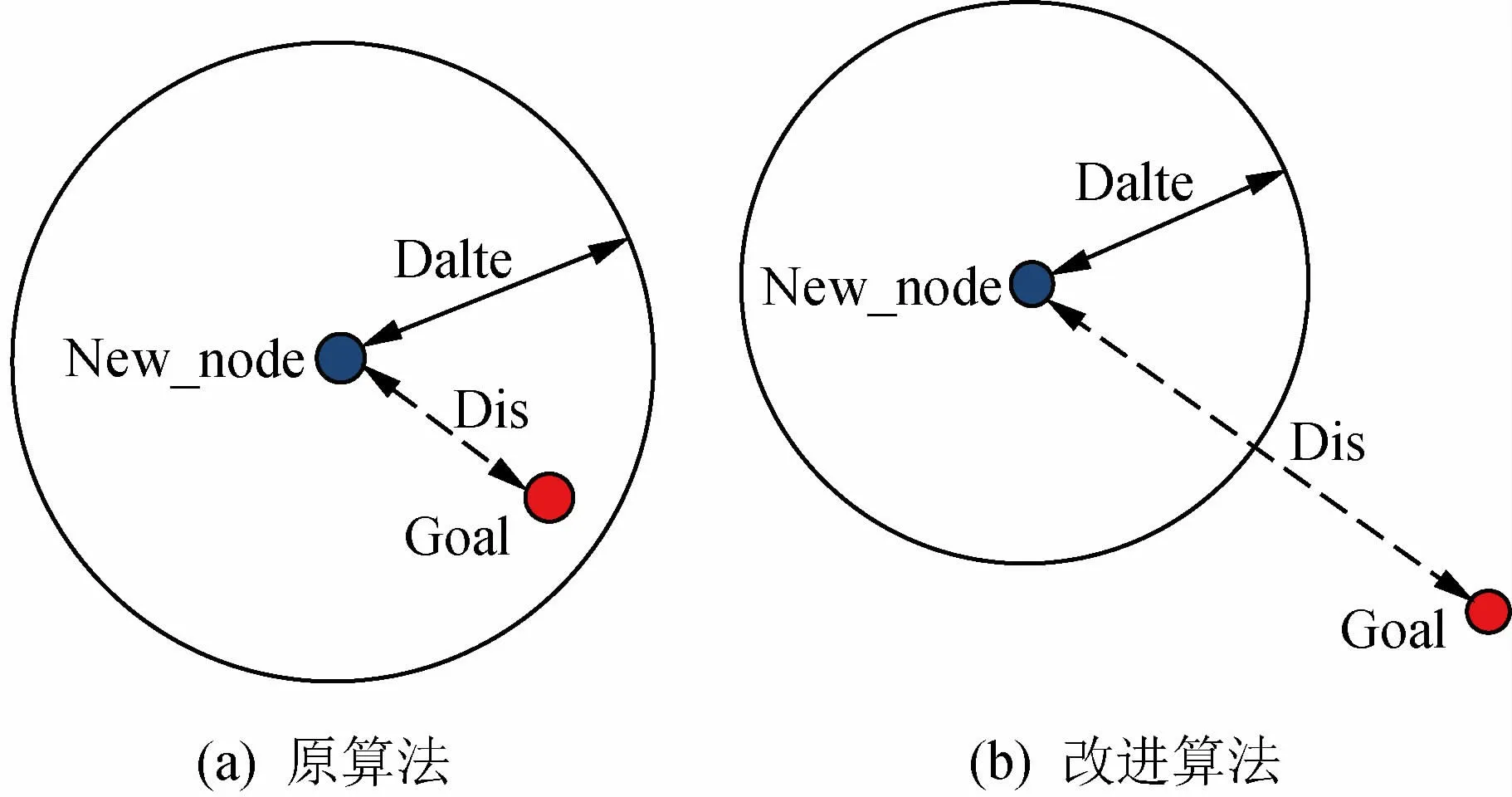
图5 搜索目标示意图Fig.5 Schematic diagram of searching target

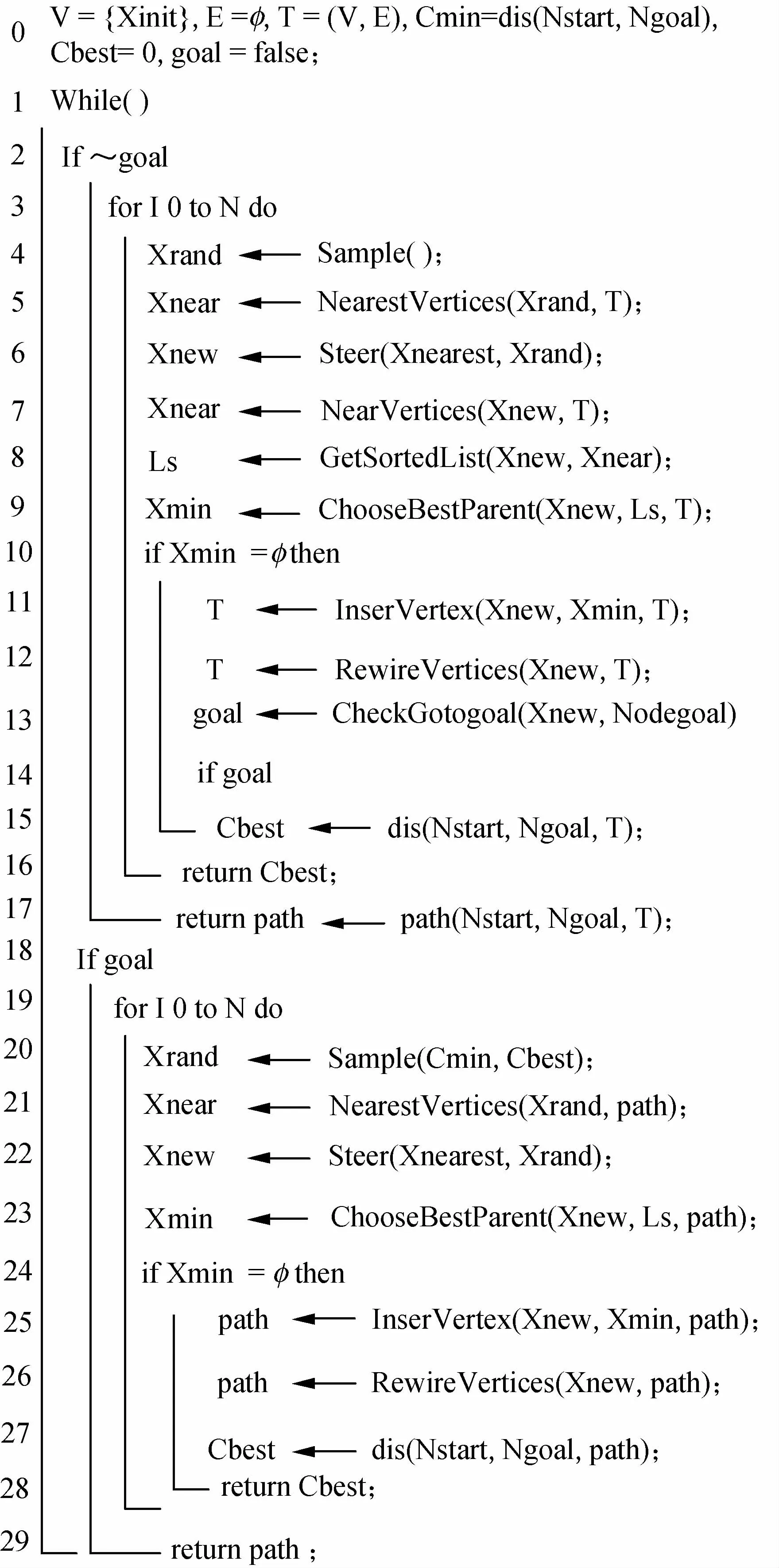
图6 改进Informed-RRT*算法伪代码Fig.6 Improved Informed-RRT*algorithm pseudo-code

3.2 搜索对象的优化

在Informed-RRT*算法的路径优化过程中对潜在最优父节点的搜索对象是路径规划过程中构成的节点树，潜在的最优父节点数量只有少数几个，检测过程中需要检测所有节点，因此存在检测多余节点会造成路径规划效率低下。本文考虑将搜索潜在最优父节点的搜索对象从节点树替换成路径。

代码如图6（第19～29行）所示。（第21行）定义规划出的待优化路径为path，在空间内采样得到采样点Xrand。若检测出Xrand点在障碍物上，则该节点被舍弃，结束本次迭代。（第22行）若Xrand点不在障碍物上，则在path列表中查找离Xrand点最近的节点Xnear。（第23行）查到Xnear 后记为path（c），然后计算Xrand到path（c）节点的距离记为delta，若delta大于SizeStep，则沿path（c）到Xrand的方向截取SizeStep长度选取一个新的点记为Xnew，若delta小于SizeStep，则Xrand节点即为要更新的节点Xnew。（第24行）得到Xnew节点后，检测path（c）是否在path列表的头部或尾部，若在path列表的头部或尾部，则Xmin为空；若不在，则Xmin非空。图7对应图6第26～27行，若Xmin非空，则比较Path（b）-Xnew-Path（d）的长度与Path（b）-Path（c）-Path（d）的长度，若Path（b）-Xnew-Path（d）长度小于Path（b）-Path（c）-Path（d）长度，则用Xnew节点代替Path中的Path（c）节点，剪枝布线获得新路径，然后重新计算Cbest，进一步缩小采样空间。

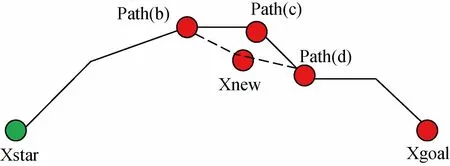
图7 改进Informed-RRT*算法路径优化示意图Fig.7 Schematic diagram of improved Informed-RRT*path optimization

4 模拟仿真实验

为了验证改进算法的有效性，本文采用MATLAB软件进行路径规划仿真实验。实验仿真区域为900 cm×700 cm的矩形，起始位置Start为（100 cm，240 cm），目标位置Goal为（800 cm，150 cm）。图8中方框表示环境内的障碍物，圆圈表示路径规划过程中采样得到的节点。实验环境根据障碍物的数量分为简单，较复杂，复杂3个等级。从规划路径的长度与时间两方面对改进前后两种路径规划算法的实验结果进行对比。

由图8可以看出，细实线为第一次规划出的路径，粗实线为在第一条路径基础上的优化路径。仿真结果表明，由于改进Informed-RRT*算法融合了贪心算法思想，因此在采样点数量上有大幅减少。

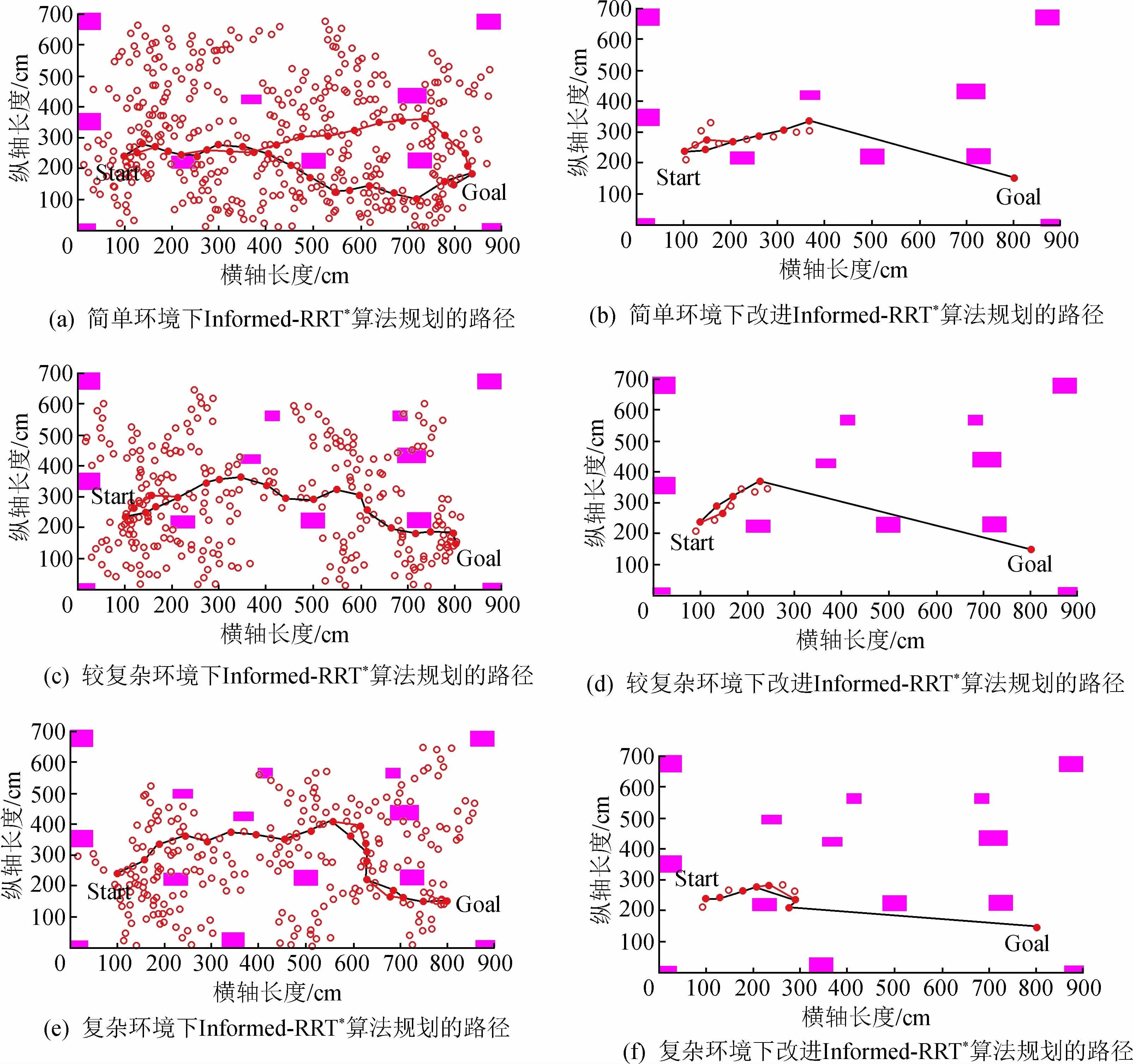
图8 改进前后两种算法在不同环境下规划的路径Fig.8 Paths planned by the two algorithms before and after improving in different environments

表1为改进前后两种路径规划算法在3种实验环境下规划路径的长度。表中实验1，2，3分别为简单环境，较复杂环境，复杂环境下的仿真实验。路径1为改进前后两种算法规划出的第一条路径，路径2为改进前后两种算法在路径优化过程中得到的路径。实验结果表明，在3种不同复杂程度的仿真实验环境下，两种路径规划算法规划出的第二条路径均比第一条路径缩短1～2 m。对比改进前后两种算法规划路径的长度，改进Informed-RRT*算法在路径规划与路径优化过程中得到的两条路径的长度均比原算法规划出的两条路径缩短10%～20%。

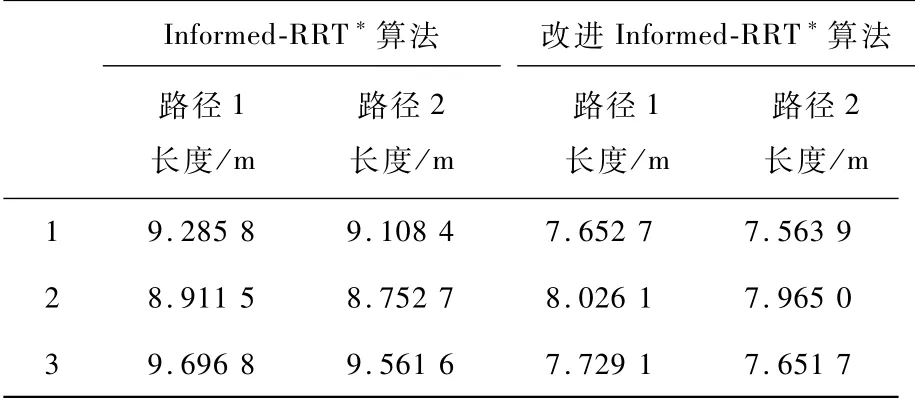
表1 改进前后两种算法在不同环境中路径长度的实验结果Tab.1 Experimental results of path length of the two algorithms before and after improving in different environments

表2为改进前后路径规划算法在3次实验中规划路径消耗的时间。在简单实验环境下，改进算法在路径规划过程中消耗的时间比原算法消耗的时间缩短了88.93%；在较复杂实验环境下，改进算法在路径规划过程中消耗的时间比原算法消耗的时间缩短了89.53%；在复杂实验环境下，改进算法路径规划消耗的时间比原算法路径规划消耗的时间缩短了83.22%。实验结果表明，在3种实验环境下改进Informed-RRT*路径规划算法在路径规划过程中消耗的时间比原算法消耗的时间缩短80%～90%。

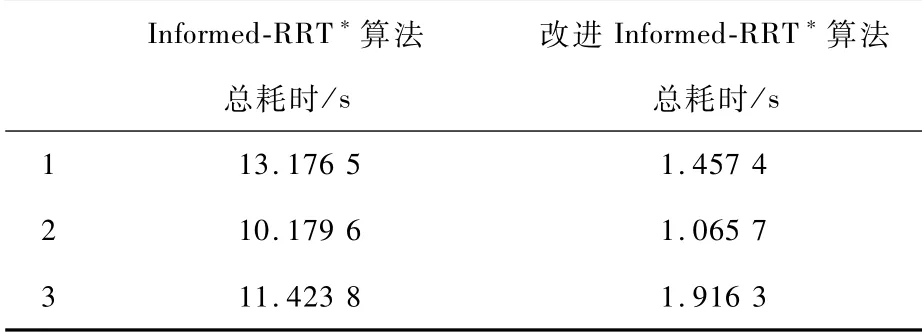
表2 改进前后两种算法在不同环境中路径规划耗时的实验结果Tab.2 Experimental results of path planning time of the two algorithms before and after improving in different environments

5 结 语

本文针对Informed-RRT*路径规划算法存在的问题，从路径规划和路径优化两个方面对Informed-RRT*路径规划算法进行优化。在3种不同复杂度的环境下进行仿真实验，结果表明，改进Informed-RRT*算法在规划路径长度与规划路径时间两方面均优于原算法，这为提高机器人自主导航效率的研究提供了理论基础。