基于粒子群模糊PID控制的自整角机伺服系统

刘祎玮，唐路平，李清源，郭迎庆，杨 蓉

(南京林业大学机械电子工程学院，江苏 南京 210000)

伺服系统作为工业生产以及基本家用电器的控制系统具有十分广泛的应用，但因其结构特性或外部干扰会导致各种误差的出现，因此需要对伺服系统制定良好的控制方案。在伺服系统的运行过程中，需要控制系统精确地调整控制参数，让输出与输入之间的误差尽可能小，且过程尽可能平稳光滑。近年来，大量学者在伺服系统的智能化控制方案的研究上取得了丰硕的成果。黄庆[1]等学者利用模糊自抗干扰控制针对永磁电动机的伺服系统进行优化控制并取得了良好的控制效果；张明月[2]等学者采用改进的自抗干扰控制系统针对电动舵机的伺服系统大大改善了系统的稳态均方差；屈毅[4]等学者针对温室采用RBF神经网络优化的PID控制器进行调控，提高了系统的辨识精度且提高了系统的自适应能力；齐霁[6]等学者利用模糊神经网络对电网的智能化调度进行了相应的实验，并取得了良好的系统控制效果。

因此，为研究伺服控制系统智能化控制研究方案，选取自整角机的伺服系统作为研究对象。采用粒子群优化算法对模糊控制进行参数优化，通过对量化因子Cke、比例因子Ckp、Cki、Ckd进行粒子群迭代寻优然后将其送入模糊控制中的模糊化与反模糊化模块处理最终得出最佳权重因子。本次实验选取RBF神经网络、模糊控制、以及传统的PID控制进行数据比较，发现该智能化控制方案可以相应地提高系统的动态性能以及控制精度，且由于该控制系统结构简单，容易实现，因此有望被应用于实际的伺服系统的控制当中。

2 自整角机的结构及工作原理

自整角机能够将角信号与电信号进行转化，可用于操控远距离仪器的转角，两台自整角机相互配合可以进行远距离的角信号发送与接收，因此往往将其应用于军事领域，如雷达扫描系统，望远镜系统等[8]。本次实验选取自整角机位置伺服系统作为研究对象，系统通常由自整角机，相敏整流电路，可逆功率放大器，执行器及减速器构成。系统构成如图1所示。

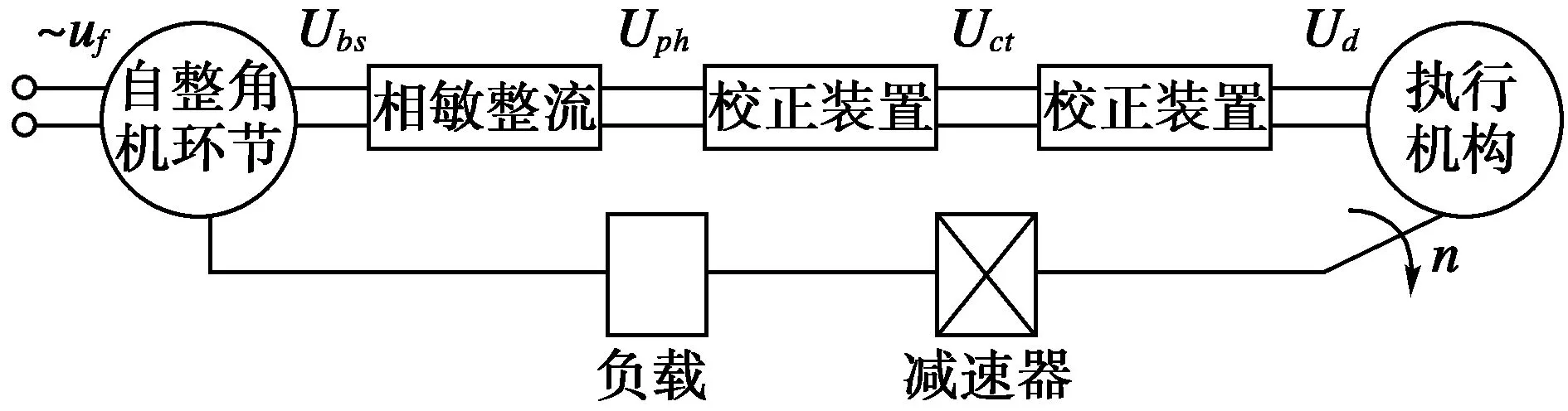
图1 自整角机伺服系统结构

自整角机环节由一对自整角机构成，其分别作为发送机与接收机进行工作，在之后加入相敏整流电路和滤波电路可以将交流信号转化为直流信号[9]。该环节的综合传递函数如下：

(1)

式中：Km为系统的滤波系数；Tph为滤波时间常数。

校正环节与前两个环节进行配合，可以提高系统的控制精度并起到消除角差的作用[10]。设矫正环节的传递函数为Wb(s)并取值为1。

可逆功放环节主要由反相放大电路及同相放大电路构成，传递函数如下：

(2)

式中：TD为可逆功率放大器时间常数，Ks为可逆环节增益系数。

执行机构选用直流伺服电机。由于电枢电路一般没有电感，电磁时间常数趋于零，可以近似为一个惯性环节。因此，得到执行器的传递函数为：

(3)

式中：Tm为系统的机电时间常数，1/Ce为电机电动势系数

减速器可以影响系统的快速性故需要选取合适的速比，传递函数如下：

(4)

式中：Kg为减速器增益系数，Kg=6/i。

综上所述，将上述环节传递函数进行整合并进行化简得到系统总的传递函数如下：

(5)

式中：T1是由可逆功率放大器时间常数与滤波时间常数合并构成，T1=TD+Tph。

综上，我们得到了自整角机伺服系统的传递函数，可由此建立相应的控制对象模型，并进行后续智能化控制系统的仿真分析。

3 控制系统的设计

3.1 RBF神经网络的设计

RBF神经网络又称径向基神经网络，是由输入层，隐含层和输出层构成的前馈神经网络。它具有自学习功能和逼近任意函数的特点。通过学习和训练，权值和参数可以在线调整，以达到最佳输出[11]。RBF神经网络具有操作简单、速度快、全局优化、逼近任意函数等优点。该方法计算量小，训练方法简单，有望在实际生产过程中得到应用[12]。在控制系统中，常将RBF神经网络与PID控制器结合使用。RBF神经网络的优点可以大大提高控制系统的动态性能。控制结构框图如图2所示。

图2 RBF神经网络系统结构

其中，误差变量的表达式为：

e(k)=r(k)-y(k)

(6)

控制系统输出变量u(k)以及增量式PID控制算法为：

(7)

隐含层利用RBF神经网络辨识系统得出的Jacobian信息在线调整系统参数，实现控制系统的在线自整定。其学习控制算法如下：

(8)

神经网络权值调整指标函数为：

(9)

(10)

3.2 模糊控制器的设计

模糊控制由以专家经验编辑成的模糊数据库、模糊规则库、模糊环节、模糊推理环节和解模糊环节组成[14]。模糊控制器利用量化因子Cke计算被检测系统的实际航迹与设定的期望航迹之间的偏差，得到模糊数据，并与模糊规则库进行相应的匹配分析。对模糊推理环节进行推理计算，得到系统的比例因子Ckp、Cki和Ckd，然后将比例因子导入PID控制器中，通过不断调整输入进行优化，从而完成控制系统的优化。

结合自整角机伺服系统的数学特征，以二维模糊控制算法对系统进行调控，以期望轨迹与实际轨迹的偏差e以及偏差的变化率ec作为输入变量，PID控制参数Kp、Ki、Kd作为输出量；采用七段式模糊语言将基本论域[-3，3]描述为相应的模糊子集{NB，NM，NS，Z，PS，PM，PB}与{负大，负中，负小，零，正小，正中，正大}相对应；选用对称式三角形隶属函数，去模糊化环节采用去重心法。

3.3 粒子群模糊PID控制器的设计及工作原理

粒子群优化算法可以通过迭代寻优在线调整系统参数，从而提高系统的控制精度，提高系统的动态性能[15]。其核心思想可以理解为鸟群捕食的过程。将每个粒子视为一只鸟，鸟群捕食的过程可以抽象为粒子群优化算法的优化过程。在寻优过程中，粒子具有速度和位置属性，规模为N的粒子群在D维空间中的速度向量和位置向为：

Vi=(vi1，vi2，vi3，…，vid)

Xi=(xi1，xi2，xi3，…，xid)

通过迭代寻优单独粒子的最佳值为局部最优解pt，再通过整体对比得到全局最优解gt，进而达到对系统参数的优化[16]。系统位置和速度在迭代过程中遵循如下算法更新：

Vt+1=ωvt+c1r1(pt-xt)+c2r2(gt-xt)Xt+1

=xt+vt+1

(11)

式中：速度迭代算法由社会认知、自我认知及继承部分组成。惯性因子ω代表前一时刻速度对当前时刻的作用；加速常数c1、c2分别代表个体认知和社会认知对粒子群的影响，当c1过大时容易陷入局部最优，当c2过大时容易过早的进入全局最优即早熟问题的出现[17]。权重ω迭代算法选用线性递归法，算法如下：

(12)

式中：t与tmax分别表示当前迭代次数与最大迭代次数，ωmax与ωmin分别表示最大惯性因子与最小惯性因子。系统采用ITAE指标作为适应值函数，其可以代表时间与误差的关系，适应值越小代表控制系统的性能越优良[18]，算法如下：

(13)

式中：e为实际轨迹与期望轨迹之间的误差，T为运行时间。

粒子群寻优具体过程为：

(1)初始化粒子群。将惯性因子，维度，粒子群规模，加速常数，最大迭代次数，最小适应值范围进行设定，并设定量化因子取值范围，设定全局最优解与个体最优解的初始值。

(2)不断分析和计算适合度值。在优化过程中，系统利用位置值计算自适应值，得到系统的ITAE指标。在迭代过程中，降低系统的自适应值，当自适应值达到要求标准时停止迭代。

(3)对粒子群的速度与位置进行更新。根据权重算法更新权重值并带入粒子群的迭代算法中对粒子群的速度与位置变量进行更新。

(4)设定粒子群迭代更新的终止条件。在粒子群达到最高迭代次数或满足适应值预期后，停止迭代寻优，并将迭代结果中的最佳值输出。

该控制方案选用粒子群优化算法在线调整优化模糊PID控制器的输入输出，即将量化因子Cke与比例因子Ckp、Cki、Ckd进行优化，然后通过模糊化与反模糊化处理动态的调节权重因子，可以相应的提高系统的控制精度及动态性能。控制结构框图如下：

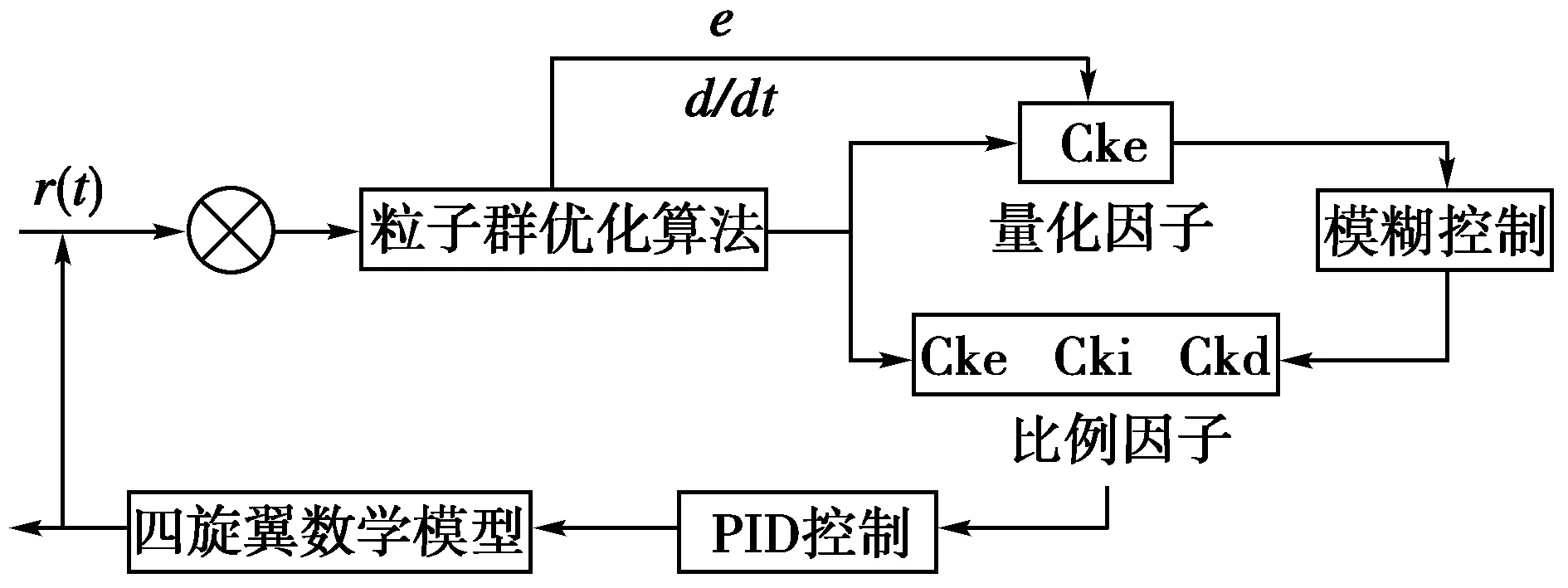
图3 粒子群模糊PID控制结构

在Matlab环境中编写程序并根据该控制结构设计搭建Simulink模型，并在此模型中对自整角机伺服系统进行实验验证。

4 实验仿真

4.1 粒子群模糊PID控制器阶跃响应实验

在Simulink搭建好仿真模型后进行实验。给予系统一阶跃响应，选取RBF神经网络PID控制器，传统PID控制器，模糊控制器进行对照仿真。

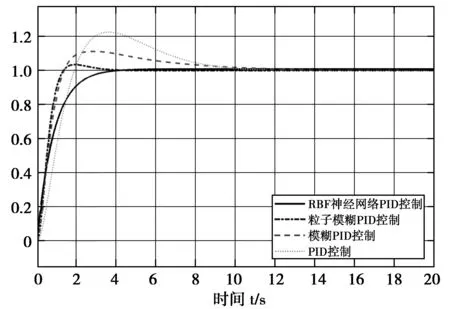
图4 粒子群模糊PID阶跃响应特性曲线

试验结果表明：在阶跃响应情况下，粒子群模糊PID控制超调量仅有3.4%，收敛速度快，在3.945 s处完成收敛。RBF神经网络面对阶跃响应也有出色的动态性能，可以做到基本无超调，但其收敛速度相对较慢。相比较而言，粒子群模糊算法具有更好的动态特性，且控制精度很高，具体数据如表1所示。

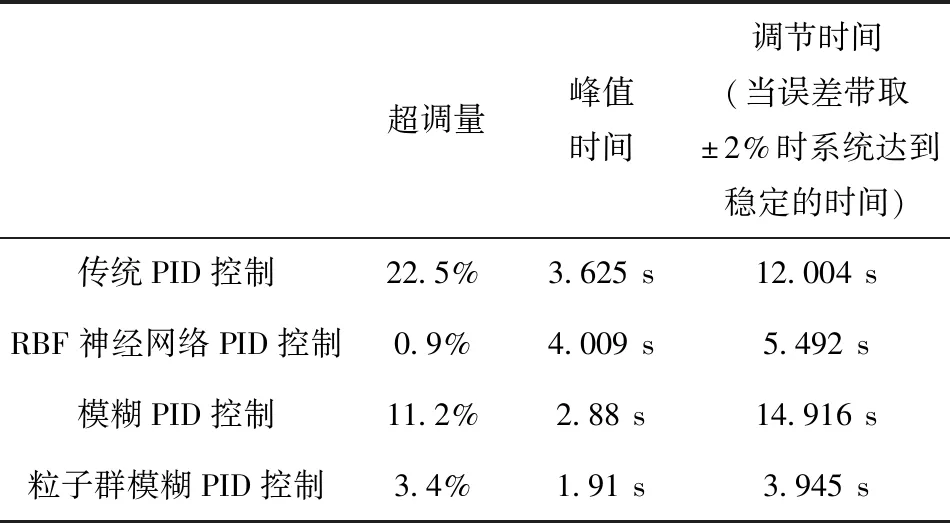
表1 各控制系统阶跃响应特性对比

4.2 粒子群模糊PID控制器角信号跟随实验

由于自整角机主要作用在对角信号的跟随问题上，因此需验证对角信号的动态响应特性，给予系统一正弦信号，观察系统响应情况。

实验结果表明，粒子群模糊PID控制的伺服系统对正弦信号具有较强的跟踪性能，跟踪时间误差仅为0.116 s，表明粒子群模糊PID控制系统具有较高的灵敏度和较快的响应速度。此外，在控制系统的控制下，几乎没有超调，证明系统的控制精度可以得到提高。具体数据见表2。

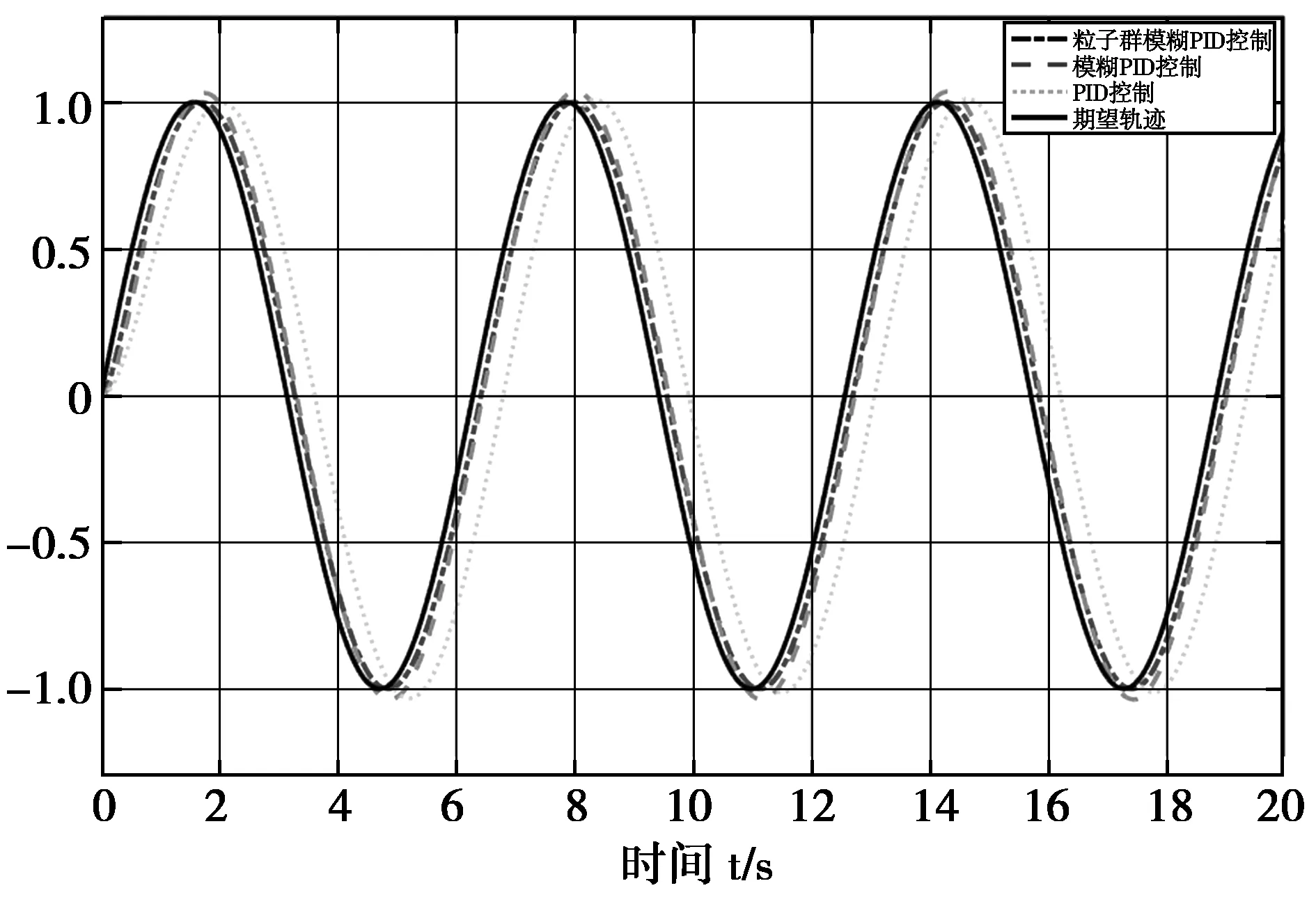
图5 粒子群模糊控制对角信号的跟踪实验

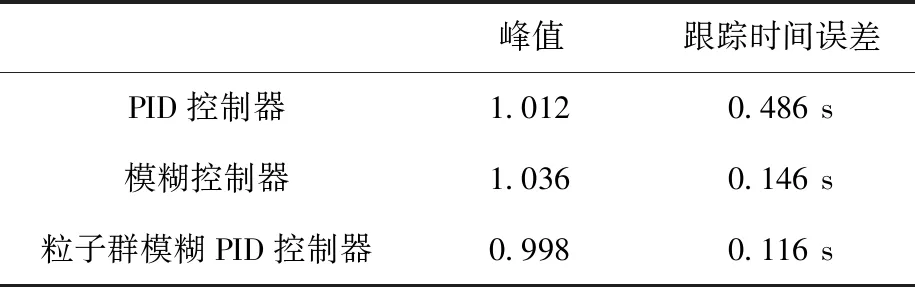
表2 各控制系统角信号跟踪数据

4.3 粒子群模糊PID控制的抗干扰性实验

因为在实际的外部生产过程中会出现大量的干扰因素，影响机器的正常运行，所以有必要对系统的抗干扰性进行实验分析。当系统稳定后，加入暂态外部干扰因子，观察系统的动态响应，如下所示：

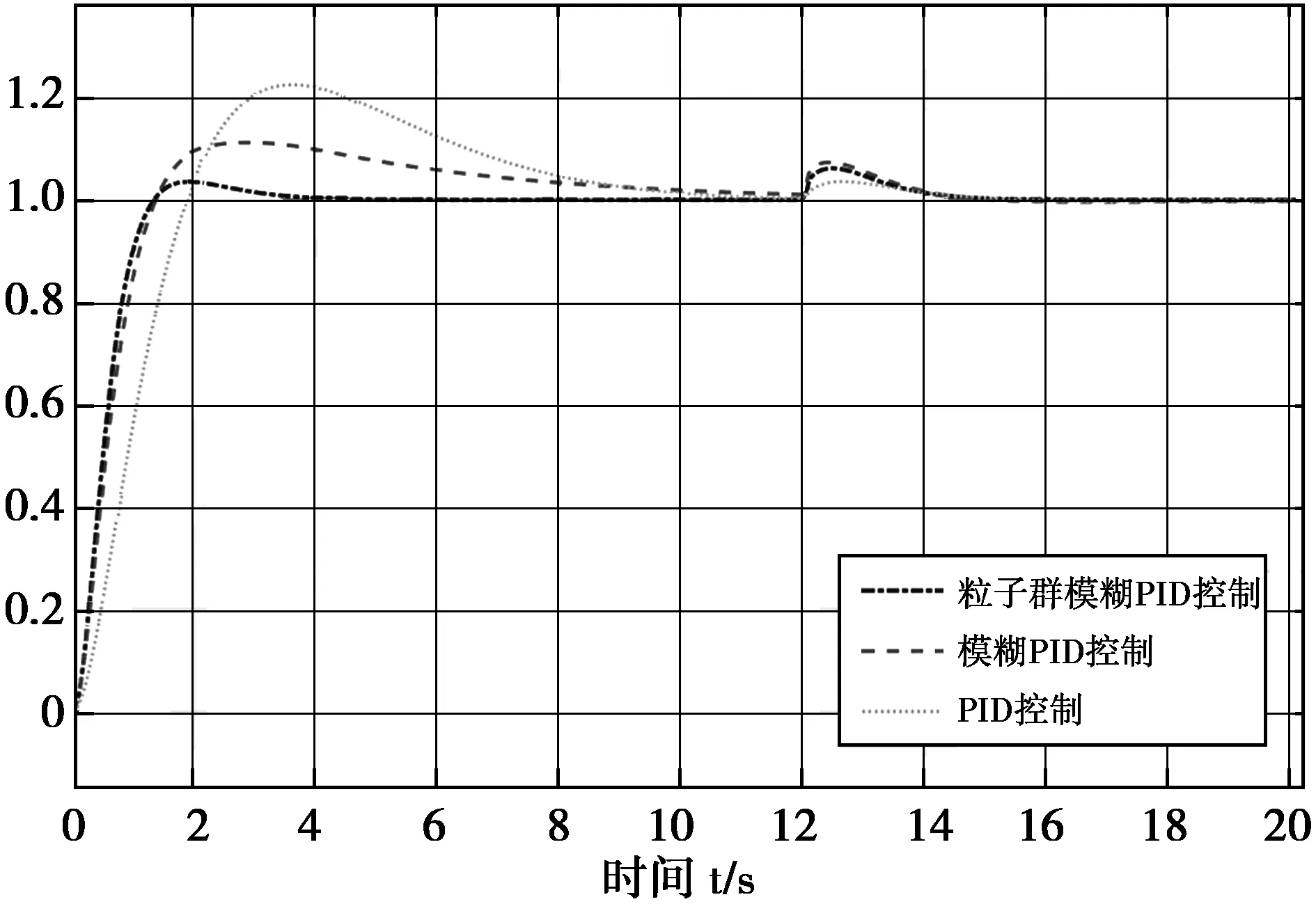
图6 粒子群模糊控制抗干扰性测试

由图中数据可知，在12 s加入50%干扰因素后，粒子群模糊控制器可以迅速调节系统，使系统能够在短暂的波动后恢复稳定。最大误差为6.2%，收敛时间为2.92 s，仅需1.71 s即可达到±2%误差区，证明了系统对于外界的干扰因素具有很强的抗干扰性，强大的稳定性。

5 结论

针对自整角机伺服系统的控制问题，本文在Matlab环境中设计了一种基于粒子群优化算法的模糊PID控制器，并与RBF神经网络，传统PID控制器及模糊PID控制器进行了实验对比。实验仿真结果表明，经过粒子群优化的粒子群模糊PID控制器具有超调量小、抗干扰性强、收敛速度快、控制精度高的优点。在面对角信号的跟踪问题时也具有很好的动态特性，可以良好地跟踪角信号轨迹。综上所述，针对自整角机的伺服系统粒子群模糊PID控制器具有良好的控制性能，对实际自整角机伺服系统的设计具有参考价值。