基于GNSS多频信号反演海平面变化研究

陈小菊，刘凯，岳国森

(1.佛山市南海区测绘成果质量检验中心，广东 佛山 528200； 2.佛山市测绘地理信息研究院，广东 佛山 528200)

1 引 言

海洋在全球生态系统的循环中发挥着至关重要的作用，传统中对海平面进行监测主要采用验潮站和卫星测高等技术，然而这些手段存在一定局限性[1]。随着GNSS的发展与深入研究，国内外学者提出利用GNSS卫星信号经地表反射后的反射信号可有效监测地表环境变化，即GNSS-R技术。Bilich等深入研究了信噪比与多路径之间的映射关系，为GNSS-R技术的发展奠定了基础[2]，Martin-Neira最先提出基于GNSS监测海平面变化，开启了GNSS-R遥感地球表面这一新的研究领域。此后Larson研究小组利用信噪比中的多路径反射分量分别进行了雪深[3]、土壤湿度[4]、植被覆盖等地表环境监测，并取得了一系列极有参考价值的研究与应用成果。Johan S.Löfgren利用GTGU、SC02、BRST、BUR2和OHI3五个观测站的数据反演海平面并分别与当地验潮站数据相比较，均取得较好数值结果[5]。在GNSS-R领域的研究，虽然国内起步略晚，但近些年国内学者同样在利用信噪比反演地表环境的研究中取得了显著研究成果[6～8]。敖敏思等利用GPS信噪比对土壤湿度进行监测并利用烘焙法得到实测土壤湿度，研究表明利用指数函数能较好地描述SNR多径延迟相位与土壤湿度之间的关系[9]。王泽民在卫星高度角范围、弧段长度、信噪比强度等因素进行研究分析，进一步提高了利用信噪比反演雪深的精度[10]。

2 GNSS信噪比反演海平面变化基本原理

在GNSS-R技术观测海平面变化的几何模型(如图1)中，部分卫星信号在传播中经反射后成为反射信号而被天线接收，尤其是对低卫星高度角的观测值影响较为明显。反射信号的干涉效应将被反映到GNSS的信噪比数据中，信噪比数据是表示接收机天线接收的卫星信号强度的一个量值。依据接收机载波跟踪环可推导出信噪比与振幅之间的关系：

(1)

由于存在反射信号干涉，向量中不仅存在直射信号的振幅Ad和相位φd，还有反射信号的振幅Ar及其相位ψ(相对于φd)，相位偏差为δφ。接收机记录的是复合信号的振幅Ac和相位φc，此时的信噪比等于复合信号的振幅。由于测量型接收机天线的扼流圈和天线增益能有效抑制因地表层反射引发的多路径效应，所以在合成信号中直射信号占主导，一般可使用低阶多项式拟合去除信噪比整体趋势项Ad，可得信噪比残差序列δ(SNR)。

从图1的几何模型中可以得出反射信号相对直射信号的路径延迟δ：

δ=2hsinβ

(2)

其中，β为卫星高度角，h指天线相位中心到水面的垂直距离。

结合式(1)和式(2)可将噪比残差序列表示为：

(3)

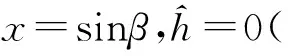
(4)

由于信噪比残差序列δ(SNR)按照历元采样，并非等间隔的sinβ函数，所以文中采用Lomb-Scargle(LS)频谱分析方法来处理非等间隔采样数据，通过对信噪比残差序列的频谱分析，获得δ(SNR)频谱能量的峰值所对应的频率f，进而求得天线至海平面的垂直反射距离h。

3 实验分析

实验数据来源于Onsala空间天文台的GTGU测站，该测站地处瑞典西海岸(57.4°N，11.9°E)，天线位于海域北侧，至海平面垂直距离约 4.3 m，在其方位60°～300°往外延伸 100 m皆为海水反射区域，测站东侧和西侧仅有部分基岩，使得最大程度上面向海域。位于GTGU测站东侧约 10 m处设有压力传感器，可通过测量来自上方水压而测得水位变化，利用此验潮数据作为参考值，如图1所示。

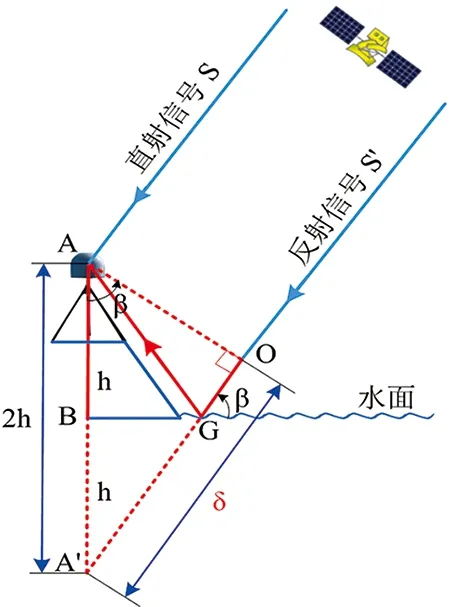
图1 GNSS-R观测海平面变化几何模型

以2020年第23天为例，图2中描述了卫星反射点在各方向上到测站的距离，同心圆为卫星反射点所对应的高度角。通过分析GPS卫星信号在测站周围的反射轨迹，可以得出卫星信号在测站周围的反射点分布情况，从而为筛选有效实验数据提供依据。文中选取方位角在70°～260°的反射信号作为有效弧段用于反演海平面变化。

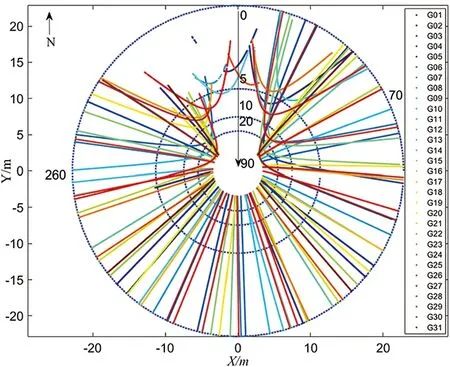
图2 卫星反射轨迹图

图3展示了有效弧段中GLONASS和GPS的SNR数据，将其去除趋势项后利用LS频谱分析可得出天线相位中心到海平面垂直距离。图4即为Lomb-Scargle频谱分析周期图，其中LSP的峰值与占主导地位的多路径频率相对应，通过式(4)得到相应的反射高度h。

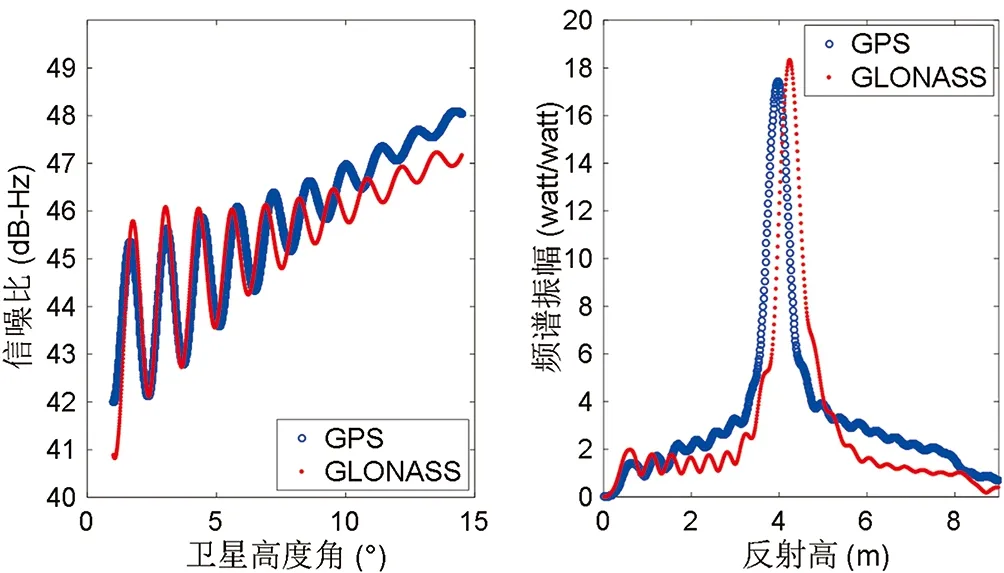
图3 信噪比 图4 Lomb-Scargle周期图

利用GTGU测站2020年doy1至doy200 GPS和GLONASS的L1和L2双频观测数据分别反演了当地海平面变化时间序列。如图5～图8分别为GPS-R和GLONASS-R实验结果，由于本文着重分析海平面变化的情况，无须求出绝对海平面高，故图中纵轴所表示的海平面变化为潮位减去其平均值的变化量。图中红色实线为验潮站所实测的海平面变化时间序列，蓝色点为GNSS-R反演值。

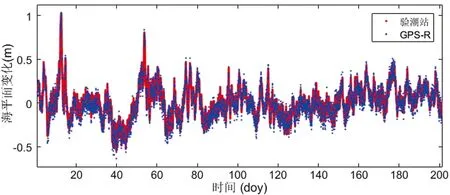
图5 GPS-R L1波段反演海平面变化

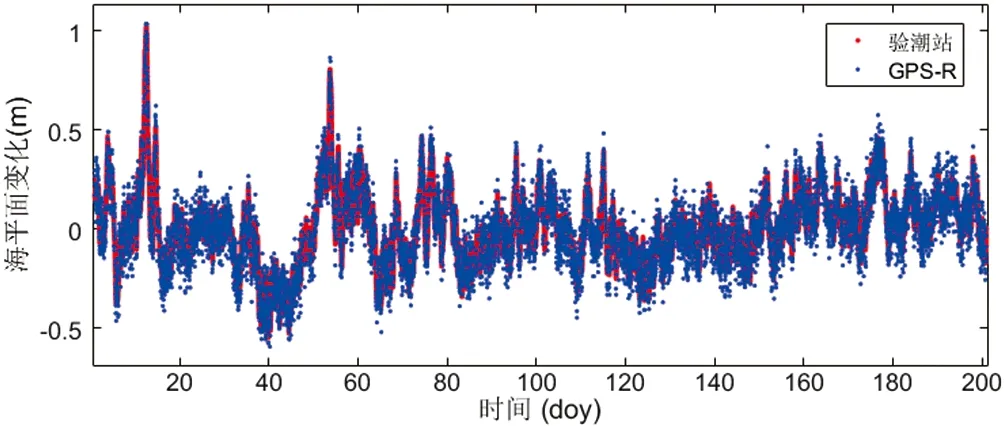
图6 GPS-R L2波段反演海平面变化

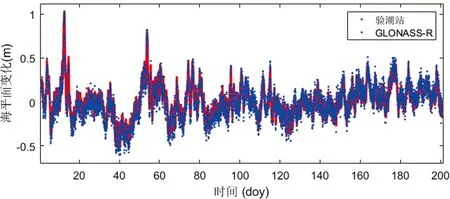
图7 GLONASS-R L1波段反演海平面变化

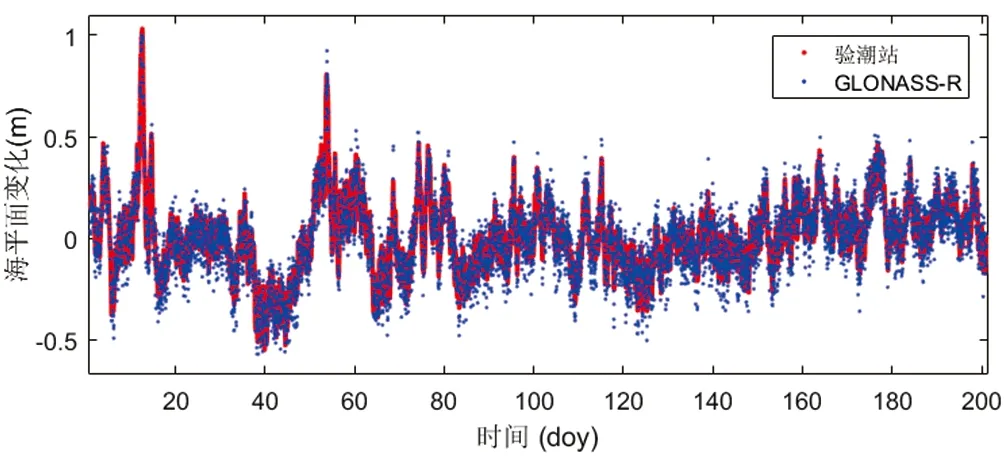
图8 GLONASS-R L2波段反演海平面变化

从图5～图8中可以看出反演结果剔除粗差后，利用GPS和GLONASS的L1和L2波段信噪比数据均可有效反演出海平面变化情况，其观测值与验潮站观测数据基本吻合。综合分析实验结果，L1波段反演值与验潮数据更为集中(如图5和图7所示)，而图8中GLONASS L2波段实验结果略差，部分与验潮数据偏离较大，但未偏离整体趋势。图6中利用GPS L2波段所得到的海平面变化时间分辨率最高，说明此测站GPS L2波段信噪比数据频谱峰值最为显著，可以得到更多有效反演结果。

从GNSS-R反演值与验潮值的相关性分析(如图9)中可以看出，GPS和GLONASS利用L1波段所得到的反演值均优于L2波段，相较于验潮数据的差值更为集中，而L2波段在海平面变化较大时比较离散，表明其反演精度略低。表1给出了GNSS-R反演海平面具体的数值分析，四组反演值均能较好反映出海平面变化情况，均方根误差均小于8cm，且与验潮数据的最小二乘相关系数均优于0.92。

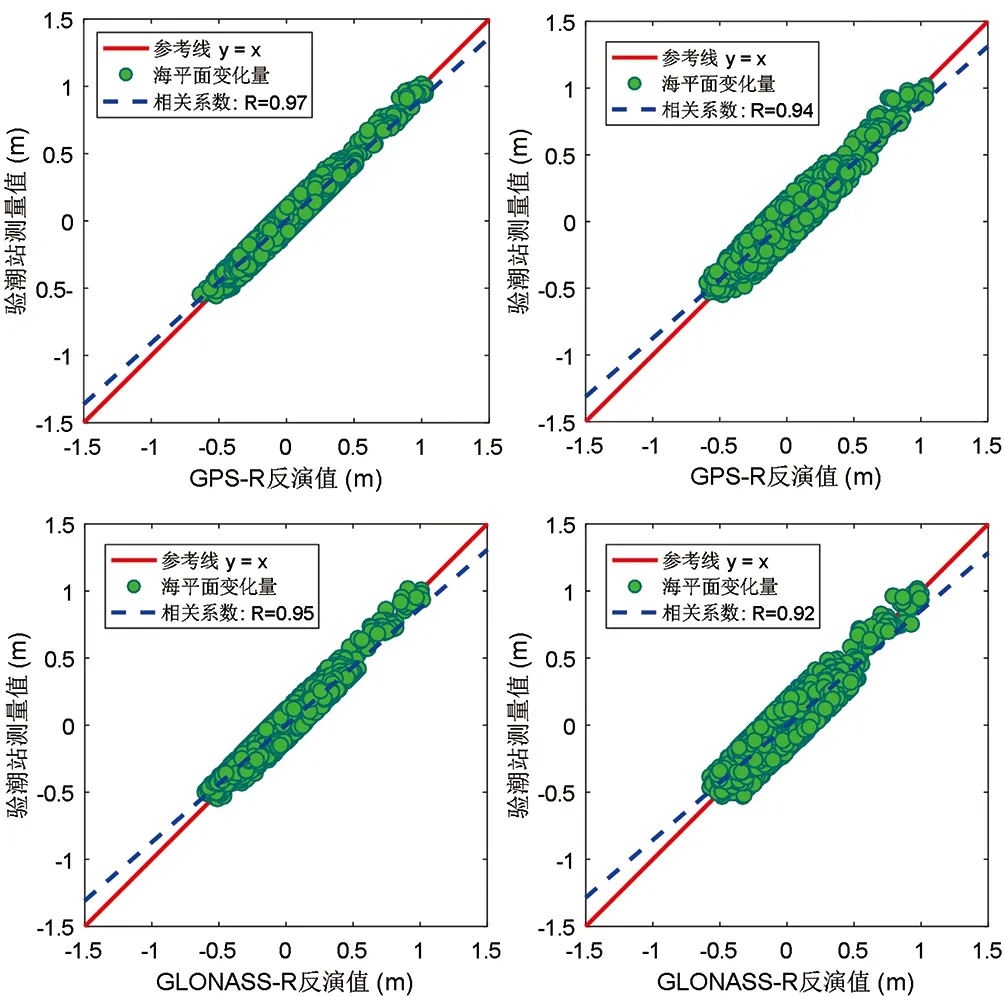
图9 GNSS-R反演值与验潮值相关性分析

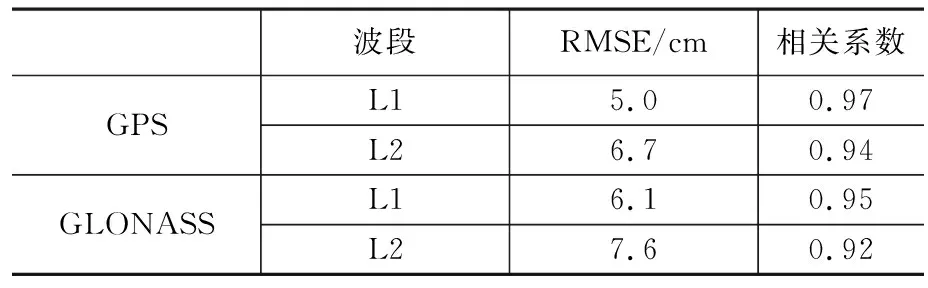
表1 GNSS-R反演海平面精度分析

4 结 论

本文以瑞典西海岸的GTGU测站为例，利用2020年长时间段的GNSS观测数据验证了GNSS-R技术用于观测海平面变化的可行性及可靠性。其中由GPS-R所得实验结果精度较高，其RMSE为 5 cm～7 cm，然而相比于GPS利用GLONASS各波段所反演实验结果误差略大，其RMSE为 6 cm～8 cm，四个波段的实验结果的相关系数均高于0.92以上。通过与验潮数据对比分析可以看出，由GPS和GLONASS的L1和L2波段所反演海平面变化均能较好地反映出海平面的变化情况。本文首次利用GPS和GLONASS的L1和L2多频观测数据对海平面进行长时间段监测，验证了GLONASS-R观测海平面变化的可靠性，且利用多频GNSS系统的信噪比对海平面进行监测，可增强监测海平面变化的多样性。