High-precision Measurements of Cosmic Curvature from Gravitational Wave and Cosmic Chronometer Observations
2022-09-02YuanHeYuPanDongPingShiJinLiShuoCaoandWeiCheng
Yuan HeYu PanDong-Ping ShiJin LiShuo Caoand Wei Cheng
1 School of Science,Chongqing University of Posts and Telecommunications,Chongqing 400065,China; panyu@cqupt.edu.cn
2 School of Electronic and Electrical Engineering,Chongqing University of Arts and Sciences,Chongqing 402160,China; dpshi@cqwu.edu.cn
3 Department of Physics and Chongqing Key Laboratory for Strongly Coupled Physics,Chongqing University,Chongqing 401331,China
4 Department of Astronomy,Beijing Normal University,Beijing 100875,China; caoshuo@bnu.edu.cn
Abstract Although the spatial curvature has been measured with very high precision,it still suffers from the well-known cosmic curvature tension.In this paper,we use an improved method to determine the cosmic curvature,by using the simulated data of binary neutron star mergers observed by the second generation space-based DECi-hertz Interferometer Gravitational-wave Observatory (DECIGO).By applying the Hubble parameter observations of cosmic chronometers to the DECIGO standard sirens,we explore different possibilities of making measurements of the cosmic curvature referring to a distant past: one is to reconstruct the Hubble parameters through the Gaussian process without the influence of hypothetical models,and the other is deriving constraints on ΩK in the framework of the non-flat Λ cold dark matter model.It is shown that in the improved method DECIGO could provide a reliable and stringent constraint on the cosmic curvature (ΩK=−0.007±0.016),while we could only expect the zero cosmic curvature to be established at the precision of ΔΩK=0.11 in the second model-dependent method.Therefore,our results indicate that in the framework of methodology proposed in this paper,the increasing number of well-measured standard sirens in DECIGO could significantly reduce the bias of estimations for cosmic curvature.Such a constraint is also comparable to the precision of Planck 2018 results with the newest cosmic microwave background (CMB) observations (ΔΩK ≈0.018),based on the concordance ΛCDM model.
Key words: (cosmology:) cosmological parameters–gravitational waves–cosmology: observations
1.Introduction
The determination of cosmic curvature is an essential topic of cosmology.Following the cosmological principles,the spacetime of our universe can be described by the Friedmann-Lemaitre-Robertson-Walker metric.Cosmic curvature can help us understand whether universe’s space is open,closed,or flat.It is worth mentioning that in the research of some scholars,the cosmic curvature is not entirely independent but depends on dark energy (Clarkson et al.2007;Wang &Mukherjee2007;Hlozek et al.2008).
To determine the cosmic curvature,scholars did some researches from two aspects.On the one hand,based on the model assumption of the cold dark matter model,it is feasible to fix the dark energy parameters in the model and introduce the cosmic curvature density parameter.In this research,the constraint result of the curvature density parameter by the Planck 2018 cosmic microwave background(CMB)is−0.095<ΩK<−0.007(Aghanim et al.2020;Di Valentino et al.2020).The constraints of CMB combined with lens and baryon acoustic oscillation (BAO)on the parameter of cosmic curvature density support the flat universe,ΩK=0.007 ±0.0019 (Aghanim et al.2020).Besides,Gao et al.(2020)studied the curvature density parameters and dark energy using the latest supernova sample.Some have proposed using Full-Shape and BAO to constrain the model with curvature parameters (Chudaykin et al.2021).On the other hand,progress has been achieved in measuring the curvature using modelindependent methods.Starting from the equation of curvature parameters,we can construct the curvature parameters at different redshifts by providing Hubble parameters (H(z)) and luminosity distances(DL)at different redshifts ΩK=(Clarkson et al.2007).This method is used as a good way to directly test the curvature parameters by bypassing the model’s hypothesis.Li et al.(2014) usedH(z) and angular diameter distance (DA(z)) given by BAO to test the curvature parameters.Supernova and quasar samples,which do not depend on model assumptions,are also suitable for these works (Gao et al.2020;Yahya et al.2014;Cai et al.2016;Li et al.2016b;Wang et al.2017;Liu et al.2020b;Jesus et al.2021;Cao et al.2019b;Wei &Melia2020).Some scholars use gravitational waves andH(z)to construct curvature at different redshifts(Zheng et al.2021).It is worth mentioning that this method needs to estimate the first and second derivatives of the luminosity distance from the fitting function,which will lead to an increase in uncertainty (Yu &Wang2016).Therefore,for the deficiency of this method,some scholars have proposed an improved model-independent method to measure curvature (Wei&Wu2017).In their research,the error caused by the derivative of luminosity distance is overcome.Since then,some scholars have used this method to test the universe’s curvature (Wei2018;Cao et al.2019a;Wei&Melia2020;Yang&Gong2021).Numerous scholars use model-independent methods to test the curvature parameters.For example,based on the distance ratio contained in the strong gravitational lensing,some scholars avoid assuming the model to test the curvature(Qi et al.2019b;Liu et al.2020a;Wang et al.2020;Zhou &Li2020;Cao et al.2022a;Wei et al.2022).Except for these ways,some scholars have tested the curvature using strong lens time delays data.(Liao et al.2017b;Qi et al.2021).It should be noted that although cosmological models do not need to be assumed in these methods,the Gaussian process used to reconstruct data may have a model dependence tendency(Colgain &Sheikh-Jabbari2021).It is worth mentioning that recently,some scholars have used machine learning methods combined withH(z) and supernova sample to test the curvature parameters ΩK=0.028±0.186 (Wang et al.2021).In their research,the method founded on the artificial neural network can overcome the a priori problem of the Hubble constant(H0).
The successful detection of gravitational waves (GW)opens a new window for cosmological research (Abbott et al.2016,2017).Looking for merging events of binary black holes or merging events of two neutron stars with electromagnetic radiation can be used as standard sirens to study cosmology (Dalal et al.2006;Hlozek et al.2008;Zhao et al.2011;Liao et al.2017a;Cai &Yang2017;Pan et al.2021;Chen et al.2021;Du&Xu2022;Chen et al.2022;Shao et al.2022).Recently,black hole-neutron star merging events have also been successfully detected(Abbott et al.2021).Moreover,the coupling coefficient between GW and matter is trifling,which can carry more primordial wave source information,which benefits cosmology.In this paper,the data from the space gravitational wave detector DECi-hertz Interferometer Gravitational wave Observatory (DECIGO) are used to simulate the gravitational wave events detected by DECIGO in the future.We use two methods to test curvature.In the former method,we directly test the curvature density parameters in the luminosity distance,but the cosmological model is not added to the luminosity distance.In the second method,we add a cosmological model including curvature to the luminosity distance and constrain the curvature density parameters in the model.First,we use the improved method proposed (Wei &Wu2017) to test the curvature.Taking into account the impact of the number of data samples on the constraints,we reconstruct the expansion rate,and the curvature parameters are constrained.Then,we utilize gravitational wave data to constrain ΩKin the framework of the nonflat Λ cold dark matter model to compare the curvature constraint effect of the two methods.In addition,in the second method,we use electromagnetic wave (EM) (supernova and quasar) data to constrain the curvature in the non-flat Λ cold dark matter model to compare with the constraints from DECIGO data.Finally,we compare and analyze the results with the researches of other scholars.
The structure of this paper is reproduced below.In Section2,we briefly introduce the data and methods we used.In Section3,we give the results and analysis.In Section4,we make a summary of this article.
2.Data and Method
2.1.Gravitational Wave Detection From DECIGO
For GW events,we know that the luminosity distance of the merging event of two stars can be obtained by detection,and the redshift information can be obtained by directly detecting the merging event with neutron stars (Holz &Hughes2005;Zhao et al.2011;Abbott et al.2017).So this kind of binary merging event can be used as a standard siren to study cosmology(Piórkowska-Kurpas et al.2021;Cao et al.2021,2022b).
DECIGO (Seto et al.2001;Kawamura et al.2006) is a GW detection project under construction in Japan,which means DECi-hertz Interferometer Gravitational wave Observatory.DECIGO’s detection frequency ranges from 0.1 to 10 Hz(Kawamura et al.2019).DECIGO has excellent detection ability.First,DECIGO in space is less affected by ground noise.Second,among the space-based gravitational wave detectors,the frequency band and objectives of DECIGO are special,its frequency band fills the gap between the sensitivity window of ground-based detectors and space detector.DECIGO is expected to measure the gravitational waves from neutron star binaries even at a redshift of 5,five years before the coalescences(Kawamura et al.2019).This means that DECIGO can estimate the time of merging and let other electromagnetic telescopes aim at the target in advance and observe other phenomena accompanied by merging,which is of great help for us to find electromagnetic counterparts.DECIGO expects to detect 10,000 neutron star binary gravitational signals a year(Kawamura et al.2019),and a large amount of data can help us better measure cosmological parameters.In this paper,we use DECIGO as the detector to simulate the standard siren information supplied by gravitational waves (see Geng et al.2020for details).
We consider two systems with massesm1andm2,whose Fourier transform can be expressed as


where ∂ameans to derive the parameter θa.It can be seen from the data released by DECIGO that it has eight equivalent detectors (Seto et al.2001;Kawamura et al.2006).Therefore,if all detectors are taken into account,the coefficient of Гabshould be eight times that of a single detector.Noise spectrum analysis from DECIGO (Kawamura et al.2006;Nishizawa et al.2010;Kawamura et al.2019):
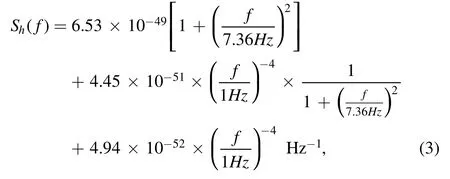
where the first line on the right represents shot noise,the second line represents radiation pressure noise,and the last line represents acceleration noise.
The relationship between the Fisher matrix and the instrumental uncertainty of the measurement of the luminosity distancecan be estimated as

wherecis the speed of light andH0is the Hubble constant.
The distribution of wave sources that can be observed on the Earth is (Sathyaprakash et al.2010;Cai &Yang2017):

whereH(z) represents the Hubble parameter,DC(z) represents the comoving distance,and the representation ofR(z) has been used in many articles (Schneider et al.2001;Cutler &Harms2006;Cai &Yang2017)

The error expression of luminosity distance is:

Through the analysis of Kawamura et al.(2019),DECIGO expects to detect more than 10,000 binary merging events every year.Based on the analysis of Cutler&Holz(2009),it is feasible to determine the redshift of these events through their electromagnetic counterparts.Therefore,we simulate the luminosity distance and the corresponding redshift of 10,000 GW events,see Figure1.

Figure 1.Luminosity distance and redshift data simulated by 10,000 GW events.

Figure 2.We reconstruct 31 Hubble parameter data from the cosmic chronometer and show its error within 1σ.
2.2.Luminosity Distance from the Cosmic Chronometer
In the Friedmann–Lemaitre–Robertson-Walker (FLRW)metric(Cao et al.2019b;Qi et al.2019a),the luminosity distance can be expressed as

ΩKrepresents the curvature density parameter andzrepresents the redshift.E(z)=H(z)/H0is given by the ratio ofH(z)toH0.H(z) (Hubble parameter) denotes the expansion rate atz,andH0is the Hubble parameter atz=0,which is called the Hubble constant.To eliminate the influence of the model,we can introduce comoving distance:
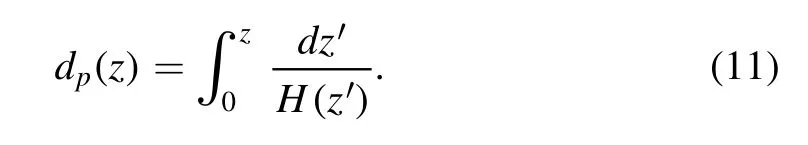
If we expressdp(z)in terms of the Hubble parameter,we can get a luminosity distance given by the Hubble parameter,

In this paper,we set the Hubble constant toH0=69.6±0.7 km s−1Mpc−1(Bennett et al.2014),so the only free parameter contained in the(z)is ΩK.We will expand the photometric distance data from the cosmic chronometer in Section2.3and combine it with the gravitational wave samples from DECIGO in Section3to test the curvature density parameters.
2.3.Gaussian Process
In this paper,to calculate the data at different redshifts at the same redshift,we use the Gaussian process method to reconstruct the data.This method was first used by Seikel et al.(2012)and has been studied by many scholars (Zhang &Li2018;Liao et al.2019;Fu et al.2013;Li et al.2016a;Wu et al.2020;Liu et al.2020b;Zhou &Li2020;Liu et al.2021).
The Gaussian process (GP) is a method of smoothing data.For the input data set,multiple smooth data in a given range can be reconstructed,and the tasks of data set expansion and redshift reconstruction can be well completed.Seikel et al.(2012) used GP to reconstruct the dark energy state parameter equation,which includes the use of GP,for which they have developed a third-party library GaPP based on Python.
In this paper,we use the Gaussian process to reconstruct Hubble parameter data.The evolution of the Hubble parameter with redshift represents the change of cosmic expansion rate with the increase of distance (Cao &Liang2013;Cao et al.2011).Jimenez&Loeb(2002)pointed out that we can use the relative galactic age to constrain the cosmological parameters,the Hubble parameter is expressed as

In this work,we use 31 redshift from 0.09 to 1.965H(z)data from cosmic-chronometer approach (Jimenez et al.2003;Simon et al.2005;Stern et al.2010;Moresco et al.2012;Moresco2015;Moresco et al.2016;Ratsimbazafy et al.2017).
We reconstruct 31 Hubble parameter data from the cosmic chronometer,and the results are shown in Figure2.In addition,we also integrate the reconstruction results and get thedp(z)and its error within 1σ,and the results are shown in Figure3.

Figure 3.We get dp(z) and its error for the reconstructed Hz integral,and the red line represents the error of dp(z) within 1σ.

Figure 4.The constraint results of the reconstructed cosmic chronometer and DECIGO on the curvature parameter.

Figure 5.Comparison of the results of four kinds of data using modelindependent method.
3.Results and Discussion
3.1.Improved Curvature Test Method
In Section2.3,we use the Gaussian process to reconstruct the Hubble parameter data and obtain the luminosity distance(z)) given by H(z).It is worth noting that the luminositydistance obtained by this method is not the same as that given by GW,so we smooth theConsidering that there may be unknown errors in gravitational wave detection,we add 10%systematic error toTherefore,we can constrain the curvature density parameter through the χ2method:

The curvature parameter result is shown in Figure4.To show the constraint effect more intuitively,we compare the constraint results of curvature parameters given by other observation data using the same method (see Table1).

Table 1The Results Obtained by Using the Model-independent Method to Constrain Curvature
As shown in Table1,the cosmic curvature density parameter,which is constrained by the luminosity distance obtained from the reconstructedH(z) and the simulated GW data from DECIGO is ΩK=−0.007±0.016.To better compare the constraint ability of DECIGO to curvature parameters.We add the research results of other scholars to the table.The constraint result given by the third generation gravitational wave detector ET is ΩK=0.035±0.039.The curvature constraint ability of DECIGO is better than that of ET.

Table 2Results of Non-flat Λ Cold Dark Matter Model with Different Data Constraints
We also show the curvature constraint results of supernovae and quasars.It is easy to see that the curvature constraint accuracy given by the GW data is more than 90% higher than that given by quasar (ΩK=0.0±0.3) and supernova sample(ΩK=0.09±0.25),respectively.In addition,we also noticed that Zheng et al.(2021) used the GW simulation data of DECIGO and ET to test the cosmic curvature,and they used the third-order logarithm polynomial approximation ofDL(z)with undetermined coefficients in their research and directly constrained the cosmic curvature through the research results of Clarkson et al.(2007).They use DECIGO (0 Figure 6.The result of constraining the non-flat Λ cold dark matter model using DECIGO and EM,respectively. Figure 7.Curvature density parameters in non-flat Λ cold dark matter model. In addition,we also investigate the constraint effect of DECIGO on curvature density parameters under the assumption of the cosmological model.The non-flat Λ cold dark matter model is, At the same time,we also combine the supernova sample(Scolnic et al.2018) with the quasar sample (Cao et al.2017a,2017b) (EM) to constrain curvature parameter to discuss the constraint effect of GW data and EM data on the curvature density parameters in the non-flat Λ cold dark matter model (see Figure6).When using the supernovae,we fix the absolute magnitude at 19.32 (Suzuki et al.2012).Meanwhile,we divide the sub-samples of simulated GW with redshifts 0 As shown in Table2,the results of constraining the non-flat Λ cold dark matter model in the table show that the curvature best values and their 68%confidence errors are ΩK=−0.012±0.11 and ΩK=−0.031±0.05 constrained by sub-sample DECIGO data at the redshift 0 to 2 and full sample atz=0 to 5 respectively.In addition,when two kinds of EM (supernova +quasar) data are used,the constraint of the curvature density parameter is ΩK=−0.034±0.15.For intuitive comparison,we also show the model-based constraint results of three kinds of data in Figure7. Our results show that in the method of directly assuming cosmological models (non-flat Λ cold dark matter model),the accuracy of curvature parameter error (ΔΩK=0.05) given by the full sample with redshift(z∊[0,5])is higher,which is only 0.5 times of the curvature error(ΔΩK=0.11)given by the subsample(z∊[0,2]),and only 0.3 times of the error(ΔΩK=0.15)given by the EM data sample.It can be seen that the error given by the full sample (z∊[0,5]) is more than twice the result of Planck data constraint ΔΩK=0.018 (Aghanim et al.2020).In addition,it is worth noting that the accuracy of the curvature parameter (ΔΩK=0.11) is lower than that of the improved curvature test method(ΔΩK=0.016)error given under the same redshift range (z∊[0,2]),as shown in Table1.However,the curvature constraint results obtained by the improved curvature test method are similar to those obtained by Planck data.For EM data,compared with the constraint result of using supernova sample alone on the model is ΩK=(Gao et al.2020),the accuracy of curvature is improved after adding quasars.However,it is still lower than those from GW data.Therefore,for gravitational waves,an improved curvature test method to constrain the curvature can be able to obtain higher accuracy results.In addition,for the constraint results of matter density parameters (Ωm) in the non-flat Λ cold dark matter model,the constraint accuracy of GW data is also higher than that of EM data,and this constraint ability becomes stronger with the increase of the number of events with the higher redshift of GW.For the Hubble constant (H0),the error results constrained by the two kinds of GW data are slightly larger than those given by EM data,but they are consistent within the 1σerror range.In particular,we use the non-flat Λ cold dark matter model to simulate the gravitational wave data and repeat the above work.The results show that the selection of curvature density parameters in the non-flat Λ cold dark matter model has little effect on testing curvature accuracy using simulated gravitational wave data. Gravitational waves as a standard siren may open up a new window for the study of cosmology,and more interesting results are expected through gravitational wave detection.In this paper,we use an improved curvature test method to study the curvature.First,31 sets of Hubble parameter data from the cosmic chronometer are reconstructed using the Gaussian process.After integrating the reconstructed data,a group of luminosity distancegiven byH(z) is obtained.Then,we use the data from DECIGO to simulate 10,000 GW events and obtain their redshift,luminosity distance,and corresponding error.By comparing the luminosity distance given by the two kinds of data,the curvature parameters are constrained.In our work,1.We simulated 10,000 GW events based on the estimation of future detection events by the DECIGO project.2.The curvature constraint results of the third generation GW detectors (ET) and the space gravitational wave detectors(DECIGO)are compared in our study.When the cosmic curvature is constrained by the improved curvature test method,ET and DECIGO get the constraint results of ΩK=0.035±0.039,ΩK=−0.007±0.016,respectively.The results demonstrate that the space gravitational wave detectors can provide a stronger constraint effect.3.We also compare the results of using the improved curvature test method and the method of using the non-flat Λ cold dark matter model to constrain curvature based on DECIGO data,which are ΩK=−0.007±0.016,ΩK=−0.031±0.05.It is shown that for DECIGO,the improved curvature test method can get a stronger constraint effect.The curvature constraint accuracy obtained by the improved curvature test method can be similar to that of curvature constraint given by Planck 2018 microwave background (ΔΩK=0.018) (Aghanim et al.2020). At the same time,we also compare the constraint results given by other observation data.Compared with the thirdgeneration gravitational wave detector ET(Wei2018),Type Ia supernovae (Gao et al.2020) and compact radio quasars (Cao et al.2019a),the error given by DECIGO is half that of ET,and the accuracy is one order of magnitude higher than that of supernovae and quasars. In addition,we also use DECIGO to constrain the non-flat Λ cold dark matter model and take the EM data as the control group.The results demonstrate that in the case of the constraint model,the curvature constraint effect of DECIGO is slightly higher than that of EM.Meanwhile,GW has excellent potential for curvature constraints under improved curvature test method conditions.By comparing the current constraint results,the gravitational wave detector DECIGO has a higher constraint ability of curvature constraints than ET and some additional current research results.At the same time,some scholars have proposed a framework including multiple measurements of gravitational waves acting as standard probes,which provides complementary model-independent constraints on the cosmic curvature with DECIGO (Zhang et al.2022).Therefore,the GW observations provide a powerful and novel method to estimate the spatial curvature in different cosmological-modelindependent ways. Acknowledgments This work was supported in part by the National Natural Science Foundation of China (Grant Nos.12105032,11873001,12047564,12075041 and 12147102);the Fundamental Research Funds for the Central Universities of China(Grant Nos.2021CDJQY-011 and 2020CDJQY-Z003);the Science Foundation of Chongqing(Grant No.D63012022005);Chongqing Science and Technology research project (Grant No.KJ111206);the Natural Science Foundation of Chongqing(Grant No.cstc2021jcyj-msxmX0481);the Scientific Research and Innovation Project of Graduate Students in Chongqing(Grant No.CYS20272).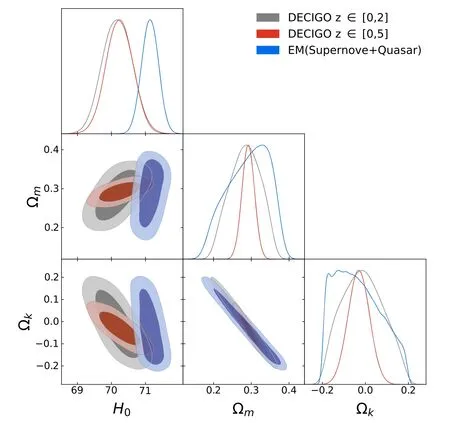

3.2.Curvature Test from Cosmological Model

4.Conclusion
杂志排行
Research in Astronomy and Astrophysics的其它文章
- A Baseline Correction Algorithm for FAST
- Ultra-wide Bandwidth Observations of 19 Pulsars with Parkes Telescope
- Correlation between Brightness Variability and Spectral Index Variability for Fermi Blazars
- HI Vertical Structure of Nearby Edge-on Galaxies from CHANG-ES
- Analyzing Dominant 13.5 and 27day Periods of Solar Terrestrial Interaction:A New Insight into Solar Cycle Activities
- Identifying Outliers in Astronomical Images with Unsupervised Machine Learning
