基于机器学习的长沙市空气污染物浓度预报研究

陈金车，迪里努尔·牙生，王田宇，王金艳，孙彩霞，谢祥珊，冯 薇

（1. 兰州市气象局，甘肃 兰州 730101；2. 兰州大学大气科学学院，甘肃 兰州 730000）

近年来，随着科技的不断进步和经济的快速发展，居民的生活水平越来越高，城市人口也在不断扩增，环境污染问题已经成为人们所关注的一个焦点。严重的大气污染不仅会对气候、植物和生态系统产生影响，还会对人们的日常出行和身体健康带来威胁[1−4]。细颗粒物是加重雾霾天气的罪魁祸首，其与雾气结合到一起使得大气能见度降低，交通事故发生的频次也随之增加[5]；高浓度的大气污染物也会通过呼吸作用进入人体组织，从而引发一系列的呼吸系统疾病和心脑血管疾病[6−9]。因此，准确预测空气污染物浓度就显得十分重要，不仅有助于提高人们的生活质量并降低损失，还可以为政府部门制定相关对策提供理论依据。

目前，国内外对于空气污染的预报方法主要分为2 种：数值预报和统计预报。数值预报模式往往要考虑污染物在大气中所经历的复杂的化学与物理过程，需要建立相对完备的气象以及排放源等相关模型，运算也比较复杂；统计预报是通过已经发生的大量历史数据进行归纳分析，寻找历史数据的特征并总结规律，从而预报出未来的大气污染物浓度，模型的构建比较简单。长沙市作为湖南省内唯一一个新一线城市 ，是湖南省经济发展的主心骨，长沙市的空气污染带来的经济损失，对整个湖南省的经济发展都会造成极大影响。因此，长沙市大气污染的预报与防治更是重中之重。

随着机器学习算法走进大气科学领域，统计预报方法更是被推上了一个新高度，最具代表性的机器学习算法包括神经网络算法、随机森林算法和支持向量机算法等。作为一个新兴领域，近些年机器学习在气象与环境污染预测等方面被广泛应用[10−12]。谢申汝等[13]通过建立支持向量机模型对大气细颗粒物进行了预测，发现输入参数的不同会对预测结果会产生较大影响；单大可[14]研究发现长短期记忆神经网络结构凭借其对时序数据较强的处理能力,可以应用于温度的精细化预报；李萍等[15]通过建立基于高斯核的支持向量机模型对北京、上海和广州3 个一线城市的空气污染指数（AQI）进行了预测，结果发现比传统预测模型的预测效果更好；陶晔[16]使用随机森林与长短期记忆神经网络相结合的方法对气温和降水进行了预测，得到了比其他方法误差更小的预测结果；孙全德等[17]通过建立机器学习模型对数值天气预报模式ECMWF 对华北地区近地面10 m 风速的预报结果进行了订正，结果发现机器学习算法在改善局地精准气象预报方面有着巨大的潜力。

本文利用空气质量监测数据和气象数据，基于支持向量机算法和随机森林算法建立SO2、NO2、O3、CO、PM10和PM2.5这6 种污染物日均浓度的预报模型，寻找出最适合于长沙地区的空气质量预报模型。

1 资料与方法

1.1 数据来源

大气污染物浓度监测数据和气象数据分别来源于环境监测站和天气后报网站（http://www.tianqihoubao.com/），选取长沙市的逐日数据，时间段 为 北 京 时 间2014 年1 月1 日 至2019 年12 月31 日，大气污染物浓度监测数据包括的要素为SO2、NO2、O3、CO、PM10和PM2.5这6 种污染物的日均浓度值；气象数据包括的要素为天气状况、最高气温、最低气温、风向和风速。首先对环境监测数据和气象数据进行质量控制，将序列中的乱码数据和缺失数据进行识别与剔除，采用相邻非缺失值线性插值的方法进行订正。

1.2 研究方法

1.2.1 归一化 由于空气污染物浓度数据以及气象数据的量纲和量纲单位存在差异，这种差异不仅会影响模型的训练速度，也会对最终的分析结果产生不利影响，因此在建立预报模型之前需要对数据进行归一化处理，使得数据被限定在一定的区间内，从而消除由奇异样本数据所带来的不利影响，提高预测精度。本研究使用公式（1）将所选数据归一化到指定区间（0，1）内，其中y代表经归一化处理之后的数据，x代表经归一化处理之前的数据，Xmax代表样本数据中的最大值，Xmin代表样本数据中的最小值，见式（1）：

1.2.2 随机森林筛选变量 通常情况下，一个数据集具有数百甚至数千种不同的特征， 在构建模型时选择对结果影响最大的属性以减少特征数量的方法已成为我们越来越关注的问题。目前在基于机器学习的大气污染物浓度预报研究中，人们常用一些方法对影响污染物浓度的因素进行重要性评估，挑选出对污染物浓度影响较大的因素作为预报因子，以此来提高预报准确率[18−23]。随机森林算法[24]可以对特征变量的重要性进行度量，尤其对于非线性问题更加适用，付旭东[25]于2020 年使用该方法对影响风场的预报因子进行了筛选，有效地提高了风场预报的准确率，该方法在污染物浓度的预测中使用较少。使用随机森林算法筛选出重要属性的思想是看每个特征对随机森林中每棵决策树的贡献程度，然后取该特征贡献的平均值，最后依据贡献值大小对每个特征进行排序。通常情况下，这种贡献大小可以通过基尼系数（Gini 系数）或者袋外数据错误率（OOB）来进行度量。

1.2.3 随机森林回归 随机森林算法是由美国加州大学的Leo Breiman 教授于2001 年提出的，单一的决策树算法在应用过程中经常会出现过拟合现象，而随机森林算法的提出可以解决此类问题。随机森林可以理解为不同的决策树应用随机处理方法所建立的算法，对于森林中的各棵决策树而言，它们彼此之间互不相关，是相互独立的个体。对于回归问题，它采用的是最小方均差原则。对于任意划分特征A 的任意划分点S，将数据集划分为S1和S2，要计算出使得S1和S2各自的均方差最小并且两者均方差和最小的特征和特征值划分点，其中，c1和c2分别为S1和S2的样本输出均值，yi为输入样本，见式（2）：

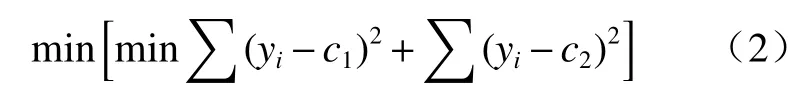
1.2.4 支持向量机回归 LIBSVM 是由台湾大学的中国学者林智仁设计发明的，并被广泛应用于分类问题和回归预测问题。传统支持向量机回归预测模型的缺陷就是只能依据经验以及对比试验来进行选取核函数与其他参数，而LIBSVM 的出现则克服了这一缺陷。与SVM 相比，LIBSVM 涉及到的参数调节更少，很多参数都是默认的，合理利用这些设置好的默认参数可用来解决许多问题，LIBSVM 还在SVM 的基础上提供了一种用于交互检验的新功能。

2 因子库的建立

2.1 基于随机森林的24 h 预报因子筛选

本文在构建污染物浓度的预报模型时，除了考虑过去5 d 的6 种污染物浓度值对次日待预测污染物浓度的影响外，还将星期效应、预测日的最高与最低气温、天气状况、风向和风速一并纳入因子库。为了降低浓度的突然波动对预测结果的影响，使得网络模型在测试数据上更加稳定，这里采用滑动平均法对污染物浓度进行3 d 滑动平均处理。在考虑星期效应时，将星期一至星期日分别用数字1～7 表示。将预测日的天气状况进行分类，分别为晴天、阴天、多云天、雾天、雨天、雪天和雨夹雪天气7 种天气类型，为了避免与星期效应产生重复对预测结果带来干扰，这里将以上天气状况分别用数字11～17 表示。将风向转化为角度值，东北风、东风、东南风、南风、西南风、西风、西北风和北风分别 用 数 字45、90、135、180、225、270、315 和360 表示，无持续风向的情况则用数字0 表示。各空气污染物浓度24 h 预报中预报因子的变量序号及其物理意义见表1。其中，X为输入变量，Y为输出变量，X1～X30 为大气污染因子，X31 为星期效应，X32～X36 为气象因子，Y1～Y6 为预测日6 种污染物的浓度值，见表1。

表1 大气污染物浓度24 h 预报中预报因子的变量序号及其物理意义

计算出长沙市24 h 预报中影响SO2、NO2、O3、CO、PM10和PM2.5浓度的因子重要性系数，以SO2和NO2为例，见图1。

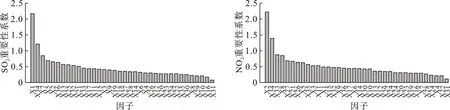
图1 长沙市24 h 预报中影响SO2、NO2 浓度的因子重要性系数

用随机森林重要性评估的方法挑选出对SO2质量浓度影响较大的因子共计23 个（相对重要性系数累计值≥80%），排名在前3 位的预报因子依次为前1 d 的SO2浓度、预测日的天气状况和前2 d的SO2浓度；挑选出对NO2质量浓度影响较大的因子共计23 个，排名在前3 位的预报因子依次为前1 d 的NO2浓度、预测日的天气状况和预测日的最低气温。同理，可以挑选出对O3质量浓度影响较大的因子共计24 个，排名在前3 位的预报因子依次为前1 d的O3浓度、预测日的天气状况和前2 d的O3浓度；挑选出对CO 质量浓度影响较大的因子共计24 个，排名在前3 位的预报因子依次为前1 d的CO 浓度、前1 d 的PM2.5浓度和前2 d 的CO 浓度；挑选出对PM10质量浓度影响较大的因子共计22 个，排名在前3 位的预报因子依次为前1 d 的PM10浓度、预测日的天气状况和前1 d的PM2.5浓度；挑选出对PM2.5质量浓度影响较大的因子共计20 个，排名在前3 位的预报因子为前1 d 的PM2.5浓度、前1 d 的PM10浓度和前1 d 的NO2浓度。

2.2 基于随机森林的48 h 预报因子筛选

与24 h 预报类似，将预报日向后推迟1 d，48 h预报中预报因子的变量序号保持不变，输入变量中大气污染因子（X1～X30）的物理意义由原来的前1～5 d 各污染物浓度值变为前2～6 d 各污染物浓度值,X31～X36 的物理意义不变，仍代表星期效应、预测日的最高与最低气温、天气状况、风向以及风速。预报因子的筛选过程同2.1 节，利用随机森林重要性评估的方法挑选出对SO2质量浓度影响较大的因子共计23 个（相对重要性系数累计值≥80%），排名在前3 位的预报因子依次为前2 d 的SO2浓度、预测日的天气状况和预测日的风速；挑选出对NO2质量浓度影响较大的因子共计21个，排名在前3 位的预报因子依次为前2 日的NO2浓度、预测日的天气状况和预测日的最低气温；挑选出对O3质量浓度影响较大的因子共计23 个，排名在前3 位的预报因子依次为前2 d 的O3浓度、预测日的天气状况和预测日的最高气温；挑选出对CO 质量浓度影响较大的因子共计25 个，排名在前3 位的预报因子依次为前2 d 的CO 浓度、前2 d的PM2.5浓度和前2 d 的NO2浓度；挑选出对PM10质量浓度影响较大的因子共计24 个，排名在前3 位的预报因子依次为预测日的天气状况、前2 d的PM10浓度和前2 d 的SO2浓度；挑选出对PM2.5质量浓度影响较大的因子共计24 个，排名在前3 位的预报因子依次为前2 d 的PM2.5浓度、前2 d的NO2浓度和预测日的天气状况。

总的来说，当以某种污染物浓度作为输出变量时，前1 d 的该污染物浓度（24 h 预报）和前2 d 的该污染物浓度（48 h 预报）对预报结果的贡献最大；不论是24 h 还是48 h 预报，预测日的天气状况都是一个不容忽视的预报因子，其重要程度在大部分预报模型中排名第2，但其对CO 预报的贡献较小，这可能与诸多的人为排放源有关；星期效应在长沙市空气污染预报中的重要程度较低，因此在选取预报因子时可不予考虑。

3 结果与分析

利用随机森林算法和支持向量机算法的回归原理建立空气污染物浓度预报模型。将数据集划分为2 个部分：训练数据和测试数据，其中训练数据和测试数据又各自包含输入数据和输出数据。选取2014 年1 月1 日至2018 年12 月31 日合适时间段的数据作为训练数据，2019 年1 月1 日至2019 年12 月31 日的数据作为测试数据，以此来构建基于机器学习的空气污染物浓度预报模型。

（1）调入数据，对数据进行归一化处理。

（2）从训练数据中选取合适时间段的特征变量采用随机森林算法和支持向量机算法分别训练模型，形成不同预报时效空气污染物浓度预报模型。

（3）将测试数据中的输入数据输入到已经训练好的预报模型中，输出经模型预报的空气污染物浓度数据。

（4）反归一化，得到空气污染物浓度预报值的最终结果。

（5）对模型输出的空气污染物浓度预报结果进行误差检验，评价不同污染过程、不同模型和不同方案下的预报效果。

3.1 典型个例分析

根据污染类型的不同，可将2019 年24 h 预报中的测试数据划分为优、良、轻度污染、中度及以上污染4 个部分进行讨论，研究在不同的污染类型下基于2 种机器学习算法的回归模型对各种污染物浓度的预报效果。

3.1.1 空气质量为优 2019 年长沙市空气质量为优的天数为117 d，当空气质量为优时，各污染物浓度真实值与预报值随时间的变化，见图2。

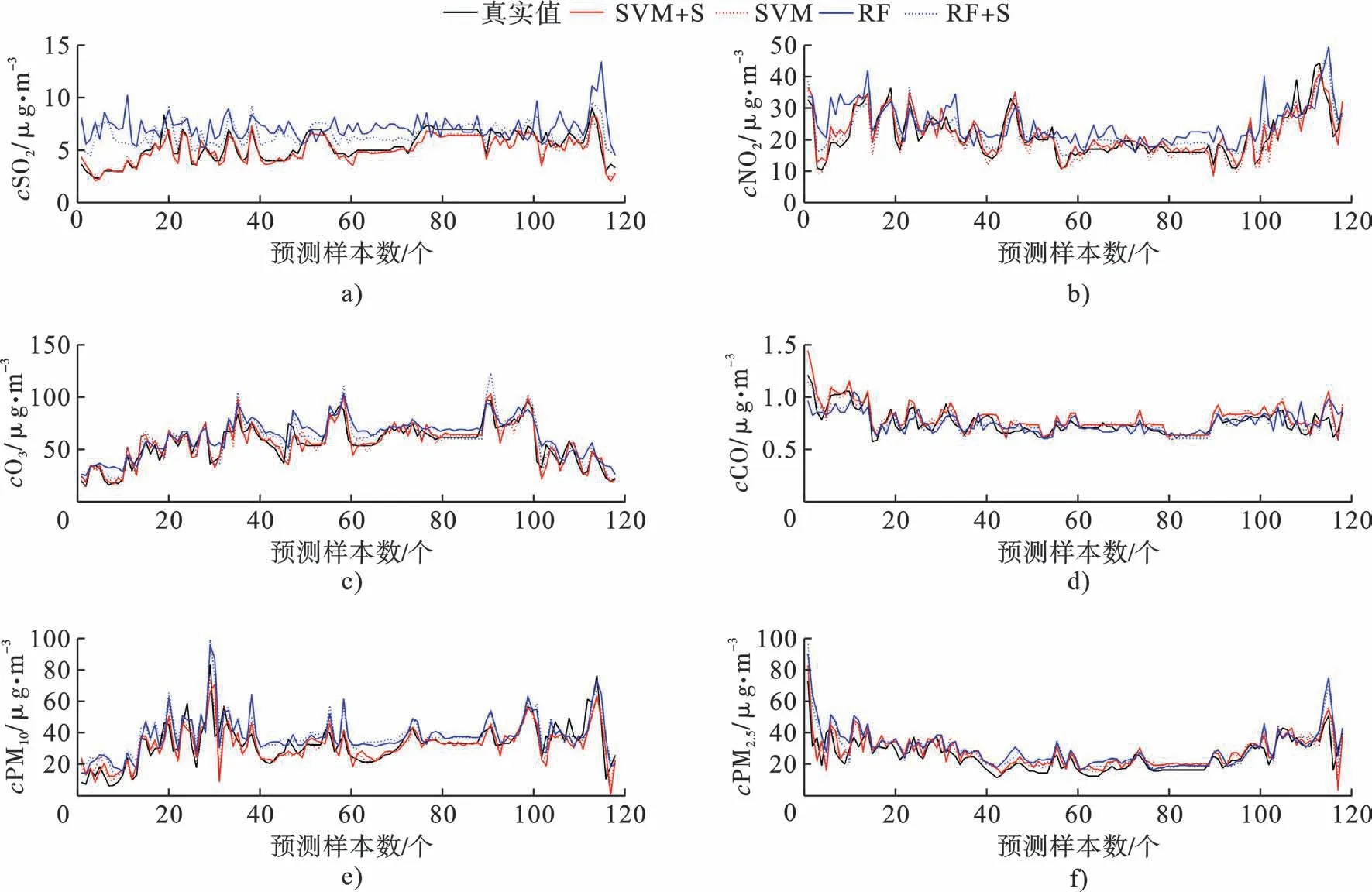
图2 空气质量为优时真实值与预报值的对比

SVM 表示经支持向量机输出的预报值；SVM+S 表示筛选变量优化之后经支持向量机输出的预报值；RF 表示经随机森林输出的预报值；RF+S 表示筛选变量优化之后经随机森林输出的预报值。图2可知，对于SO2和PM10而言，支持向量机模型的预报值偏低，随机森林模型的预报值偏高，而CO 则恰恰相反；对于NO2而言，优化后支持向量机模型的预报值偏低，随机森林模型和优化前支持向量机模型的预报值偏高；对于O3和PM2.5而言，支持向量机模型和随机森林模型的预报值都偏高。

空气质量为优时各预报模型的均方根误差分布，见表2。

表2 空气质量为优时各预报模型的均方根误差分布

表2 可知，变量筛选优化之后的支持向量机模型对SO2、NO2、O3、PM10和PM2.5浓度预报效果最好，预报结果的均方根误差最小；变量筛选优化之后的随机森林模型对CO 浓度预报效果最好，预报结果的均方根误差仅为0.063 mg/m3，变量筛选优化之后的支持向量机模型对CO 浓度预报效果次之，预报结果的均方根误差为0.065 mg/m3。

3.1.2 空气质量为良 2019 年长沙市空气质量为良的天数为200 d，当空气质量为良时，各污染物浓度真实值与预报值随时间的变化，见图3。

图3 可知，对于SO2而言，支持向量机模型的预报值偏低，随机森林模型的预报值偏高，而CO则恰恰相反；对于NO2而言，优化后支持向量机和优化前随机森林模型的预报值偏低，优化前支持向量机和优化后随机森林模型的预报值偏高；对于O3和PM10而言，支持向量机和随机森林模型的预报值都偏低；对于PM2.5而言，优化前的预报值都偏高，而优化后的预报值都偏低。

空气质量为良时各预报模型的均方根误差分布，见表3。

表3 空气质量为良时各预报模型的均方根误差分布

表3 可知，变量筛选优化之后的支持向量机模型对SO2、NO2、O3、PM10和PM2.5浓度预报结果的均方根误差最小；变量筛选优化之后的随机森林模型对CO 浓度预报结果的均方根误差最小，其次为变量筛选优化之后的支持向量机模型。

3.1.3 空气质量为轻度污染 2019 年长沙市空气质量为轻度污染的天数为29 d，当空气质量为轻度污染时，各污染物浓度真实值与预报值随时间的变化，见图4。对于SO2和而言，支持向量机模型的预报值偏低，随机森林模型的预报值偏高，而CO 和PM2.5则恰恰相反；对于NO2而言，优化后支持向量机模型和优化前随机森林模型的预报值偏低，优化前支持向量机模型和优化后随机森林模型的预报值偏高；对于O3而言，优化前的预报值都偏低，而优化后的预报值都偏高；对于PM10而言，除优化前随机森林模型的预报值偏高外，其余模型的预报值都偏低。空气质量为轻度污染时各预报模型的均方根误差分布，见表4。

表4 空气质量为轻度污染时各预报模型的均方根误差分布

图4 空气质量为轻度污染时真实值与预报值的对比

表4 可知，变量筛选优化之后的支持向量机模型对NO2、O3、PM10和PM2.5浓度的预报效果最好；变量筛选优化之后的随机森林模型对CO 浓度的预报效果最好；变量筛选优化之前的支持向量机模型对SO2浓度的预报效果最好。

3.1.4 空气质量为中度及以上污染 2019 年长沙市空气质量为中度及以上污染的天数为19 d，当空气质量为中度及以上污染时，各污染物浓度真实值与预报值随时间的变化，见图5。对于SO2和PM10而言，支持向量机模型的预报值偏低，随机森林模型的预报值偏高，CO 反之；对于NO2而言，各模型的预报值都偏高；对于O3而言，除了优化前支持向量机模型的预报值偏高外，其余模型的预报值都偏低；对于PM2.5而言，各模型的预报值都偏低。空气质量为中度及以上污染时各预报模型的均方根误差分布，见表5。

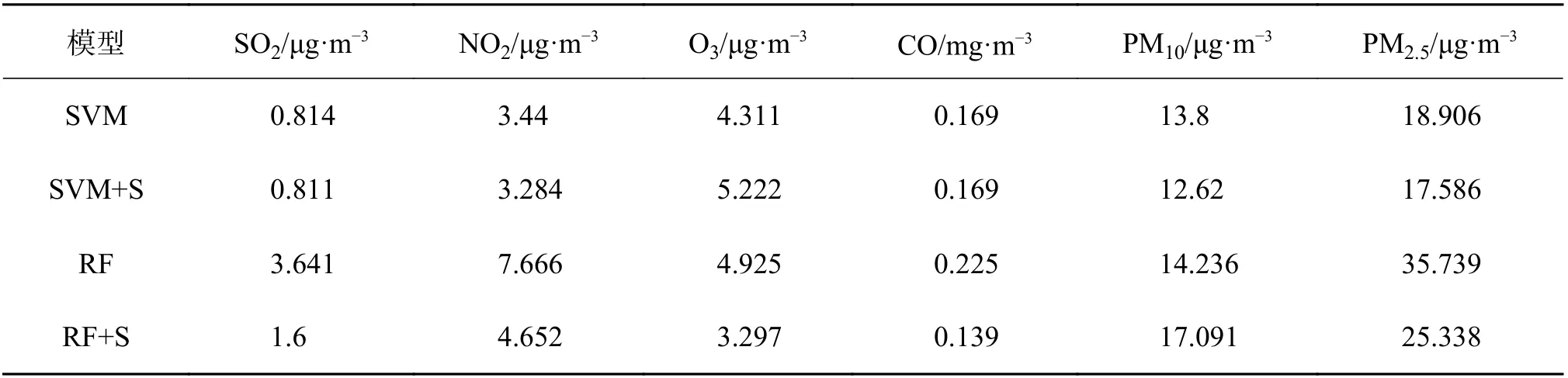
表5 空气质量为中度污染及以上时各预报模型的均方根误差分布

图5 空气质量为中度污染及以上时真实值与预报值的对比

变量筛选优化之后的支持向量机模型对SO2、NO2、PM10和PM2.5浓度的预报效果最好；变量筛选优化之后的随机森林模型对O3和CO 浓度的预报效果最好。

不同污染等级下4 种方法预报结果均方根误差的均值分布，见表6。

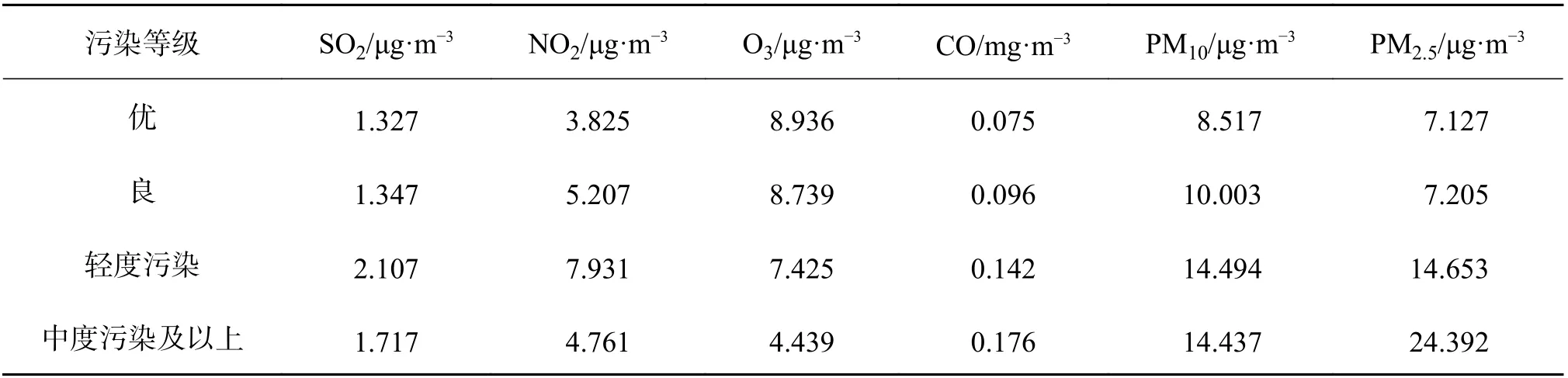
表6 不同污染等级下4 种方法预报结果均方根误差的均值分布

空气质量在优、良、轻度污染时，SO2、NO2、CO、PM10和PM2.5浓度预报结果的均方根误差随着AQI 指数的增大而增大，然而到了中度污染及以上时，SO2、NO2和PM10浓度预报结果的均方根误差反而减小，这可能与数据样本量过小有关，由于测试数据中长沙市空气质量为中度及以上污染的天数仅仅只有19 d，远小于其他污染类型的天数，因此带来了偶然性。

3.2 长时间预报效果检验

基于随机森林和支持向量机2 种机器学习算法，分别将随机森林重要性评估法挑选出的预报因子和未经挑选的预报因子作为预报模型的输入变量，对2019 年一整年这6 种空气污染物的浓度分别进行预报，得到预报结果。2 种方案24 h和48 h 预报结果的误差评价指标对比，见表7 和表8，为了便于叙述，将未经预报因子筛选的方案定义为方案A，经过预报因子筛选的方案定义为方案B。

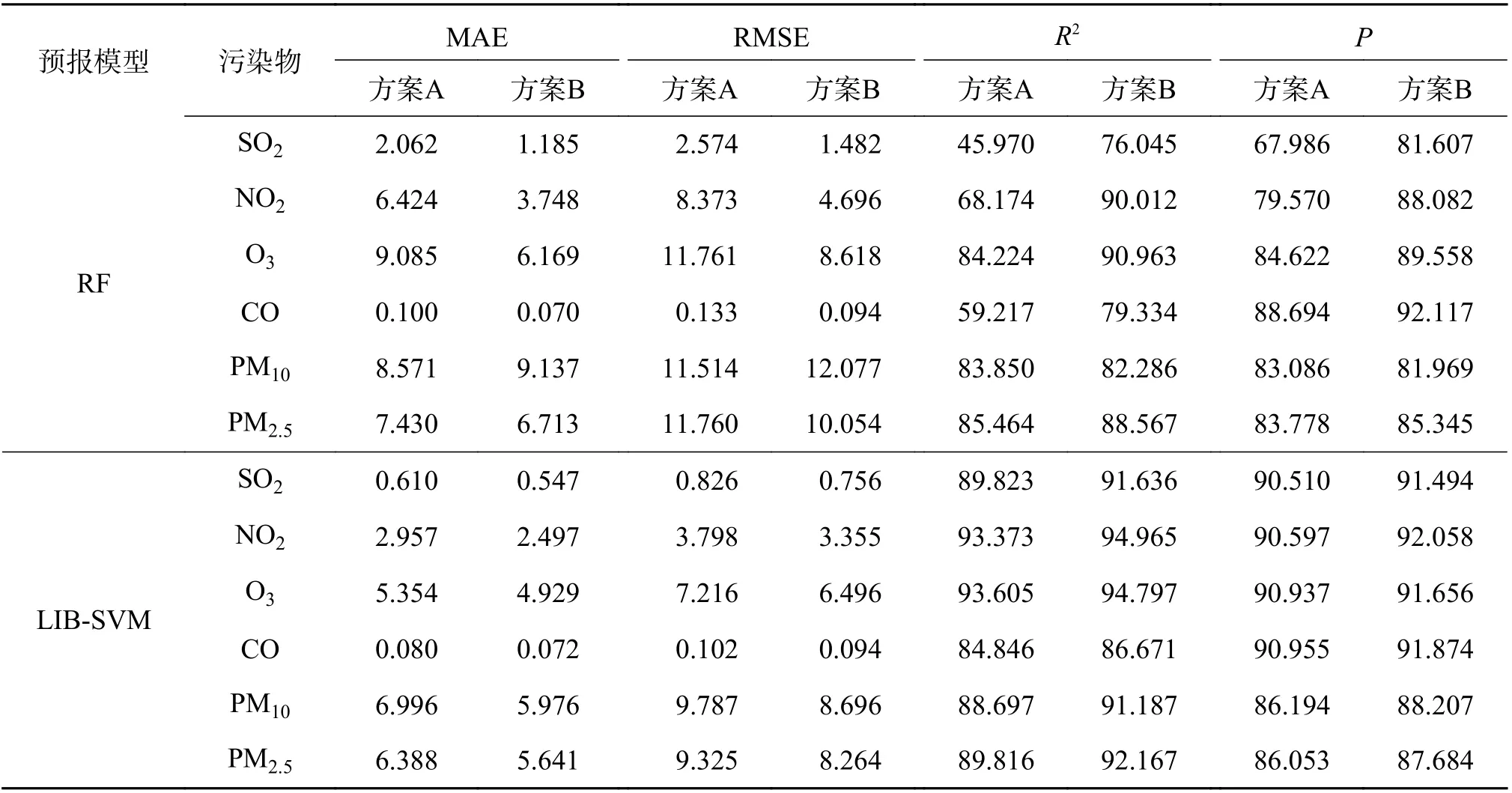
表7 2 种方案24 h 预报结果的评价指标对比

表8 2 种方案48h 预报结果的评价指标对比

表7 和表8 可知，在24 h 预报中，对于随机森林预报模型而言，除了PM10预报结果的平均绝对误差和均方根误差方案B 大于方案A，判定系数和准确率方案B 小于方案A 以外，其余指标的预报结果均表明方案B 优于方案A；对于支持向量机预报模型而言，所有指标的预报结果均表明方案B 优于方案A。在48 h 预报中，对于随机森林预报模型而言，除了NO2预报结果的均方根误差方案B 稍大于方案A，判定系数方案B 稍小于方案A 以外，其余指标的预报结果均表明方案B 优于方案A；对于支持向量机预报模型而言，所有指标的预报结果均表明方案B 优于方案A，这与24 h 预报中所得到的结论一致。整体而言，经随机森林筛选变量对模型进行优化之后，可有效提高模型的预报性能，提高准确率。

4 结论

文章基于长沙市2014～2019 年的空气污染资料与气象资料，利用随机森林重要性评估的方法对预报因子进行了筛选，结合支持向量机回归模型和随机森林回归模型对6 种污染物浓度分别进行了预报。

（1）在诸多预报因子中，前日的污染物浓度对该污染物预报的贡献最大，其次是预测日的天气状况，长沙市空气质量预报受星期效应的影响较小，在建立预报因子库时可将其忽略。

（2）AQI 指数越高，预报结果的均方根误差越大，且各模型的预报准确率随着预报时效的增加而减小。

（3）LIBSVM 模型在长沙市空气质量预报中较RF 模型有更强的泛化能力，预报结果的误差更小，准确率更高，且经随机森林筛选变量对预报模型进行优化可有效提高预报准确率，因此可将随机森林筛选预报因子的支持向量机回归模型推广至长沙市空气质量预报的业务中，可为长沙市空气质量业务化预报提供技术支撑和防控依据。