基于DHIM映射和分块置乱的彩色图像加密算法

代高乐，葛 斌

（安徽理工大学 计算机科学与工程学院，安徽 淮南 232001）

1 引言

近年来，通信技术的飞速发展，给人们生活带来了极大的便利，但同时也伴随着个人隐私泄露的可能，信息网络安全也成为当下热门的话题。数字图像作为一种常用的信息传输媒介，是隐私安全主要保护对象，而保护图像数据的安全最直接有效的方法就是图像加密。DES、RSA和IDEA[1,2]等都是具有极为优秀的加密算法，但这些算法在一般情况下用于文本加密，针对数字图像这种数据量大、冗余度高和相关性高的特点，需要有专门的加密算法进行加密。

目前，许多加密算法被陆续提出，大多是基于混沌映射和置乱扩散相结合的图像加密算法。Ban[3]等人提出SPM映射，用sine映射与模运算结合调制PWLCM映射，扩大了混沌映射的混沌区间，但混沌映射的随机性较差。Gao[4]提出一种改进的Henon映射，将Henon映射与传统的无限迭代映射相乘，增加了混沌系统的控制参数从而扩大了加密算法的密钥空间，但仍存在较小的混沌区间和不平均的输出值等问题。Wang[5]等人提出利用多重混沌映射结合动态L型置乱的方法对图像进行加密，但处理较大图像的效率较低。基于以上几点问题，本文通过增加动态控制参数增大混沌区间，且高效利用混沌序列，采用分块的方法块间置乱、块内置乱提高加密效率。

2 混沌映射的设计与性能评估

混沌因其具有不可预测性、内在随机性、长期不可预测性和对初始值的敏感性等优点，被广泛应用于图像加密中。本文介绍了设计的DHIM映射，并通过分岔图、李雅普诺夫指数和样本熵验证了DHIM的混沌性。

2.1 DHIM混沌映射的设计

由于传统Henon映射混沌区间小混沌、混沌行为简单，文献[4]将iterative映射与Henon映射复合，提出改进的Henon混沌映射，增强了一定区间的混沌行为，但混沌映射区间较小密钥空间不足。针对此问题，本文提出DHIM映射，用Logistic映射代替控制参数r∈[0,1]，动态控制混沌映射参数，增强了混沌行为的复杂性、增大混沌区间。DHIM映射被定义为：

其中，控制参数 a∈[-0.25,1.5]，b∈[0,0.3]，u∈[3.57,4]，令 b=0.3，u=3.99，由图 DHIM 映射在[-1,1]间处于满映射状态。

2.2 分岔图分析

分岔图的轨迹反应非线性系统的行为，描绘了系统从周期到混沌的运动轨迹。混沌映射在分岔图中映射范围越广，说明混沌映射的混沌性能越好。DHIM映射的分岔图如图1所示。

图1 DHIM分岔图

从图1中可以看出DHIM映射在a∈[-0.25,1.5]时处于混沌状态。

2.3 李雅普诺夫指数分析

李雅普诺夫指数(LE)描述了相空间中两条相邻轨迹之间的平均指数收敛或发散速率。二维混沌映射有两个LE，只要一个LE为正，说明此时混沌系统处于混沌状态，并且随着LE的增加，映射的混沌行为变得更加明显。图2展示了DHIM的李雅普诺夫指数图。

图2 样本熵

从图2中可以看出，由于在原有映射中添加了动态控制参数使得DHIM映射具有更复杂的混沌行为，李雅普诺夫指数更大，且具有两条LE皆为正数，效率更高。

2.4 样本熵测试

样本熵（Sample Entropy，SE）是通过度量信号产生新模式的概率大小来衡量时间序列复杂性，新模式产生的概率越大，序列的复杂性就越大。样本熵的大小在用来评估混沌映射产生混沌序列的复杂性具有较好的说服力。DHIM的样本熵如图3所示。

图3 DHIM样本熵

3 算法描述

本章节提出了基于DHIM分块置乱且适用于任何大小的彩色图像加密算法。该算法利用SHA-512产生与明文相关的混沌初始值与控制参数以达到一次一密的效果；对明文图像进行补零操作得到大小为(M×N)的图像以确保可以拆分为T个大小为(L×L)像素块，采用“块间-块内-块间”置乱的方式充分对像素位置进行打乱，正反两轮扩散以充分改变像素值，提高算法的安全性，如图4所示。

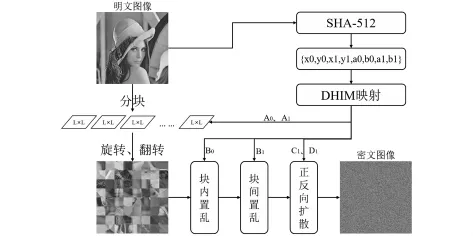
图4 加密算法流程图

3.1 初始值和控制参数的生成

Step 1：对明文图像进行SHA-512操作，得到长度为128位的密钥key，密钥为16进制字符串。

Step 2：将密钥转换为512位的二进制字符串，每 64 位为一组分为 8 组密钥值 k1、k2、k3、k4、k5、k6、k7、k8。

Step 3：令8组密钥值按照公式(3)和公式(4)所示确定本文算法中的初始值和控制参数{a0,b0,a1,b1,x0,y0,x1,y1}。

3.2 DHIM混沌序列

将上述操作得到的初始值和系统参数，代入DHIM映射中迭代数次，可得到本文算法中所需要的混沌序列：

Step 1： 将初始值 x0、y0、a0和 b0代入 DHIM 映射中迭代(500+max(T,L×L))次，L为每块的边长，T为分块的个数。舍弃前500次迭代结果以达到充分的混沌状态，得到两组混沌序列A0、B0。

Step 2：保留序列A0的前T个数，利用公式(4)对A0进行处理得到伪随机序列A1，用于块间置乱。

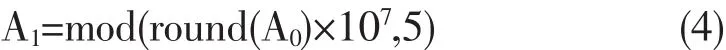
其中，mod()为模运算，round()为四舍五入。

Step 3：运用公式(5)对 B0进行处理得到 B1，并将B1重新组合成大小为(L×L)的矩阵P，用于块内置乱。

其中T为分块的个数。

Step 4： 将初始值 x1、y1、a1和 b1代入 DHIM 映射中迭代(500+M×N×3)次，舍弃前 500个数得到C0、D0，再利用公式(6)进一步处理得到新的混沌序列 C1、D1，用于两轮扩散。

其中abs()为取绝对值。

3.3 加密流程

Step 1：输入大小为的彩色图像I和块的边长L，并对明文图像进行补零操作得到大小为(M×N)的明文图像I′，确保分块大小均为(L×L)，设定L的大小为64。

Step 2： 将图像 I′拆分为 Ir、Ig、Ib 三个平面并组合成大小为(M×N×3)的矩阵S，并进行矩阵分块，每一块的大小为(L×L)。

Step 3：块间置乱。利用混沌序列A0索引排序对矩阵S进行块间排序，并根据序列A1的数值对分块矩阵进行旋转翻转，如表1所示。

表1 分块旋转翻转规则

Step 4：块内置乱。运用混沌序列B0排序后的索引，对每一块内的像素进行块内混沌置乱。

Step 5：块间置乱。将混沌序列B1组合成矩阵P，使每一分块的像素点与P中的元素一一对应，并根据P中的矩阵元素数值在每一块中循环移位，使像素在整个矩阵内充分置乱最终得到置乱后的矩阵Q。

Step 6：利用混沌序列C1构造矩阵W，根据公式(7)对矩阵Q进行第一轮正向非序列扩散得到矩阵G。其中W(i,j)为伪随机矩阵的像素值；Q(i,j)为置乱后矩阵的像素值；G(i,j)为正向扩散后矩阵的像素值。

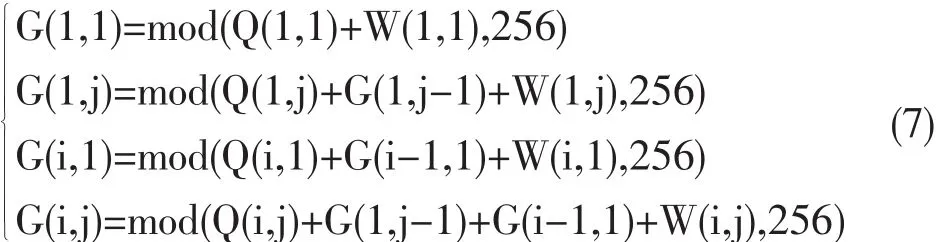
Step 7：利用混沌序列D1构造矩阵S，根据公式(8)对矩阵G进行第二轮反向非序列扩散得到矩阵E。其中S(i,j)为伪随机矩阵的像素值；E(i,j)为反向扩散后矩阵的像素值。

Step 8：依据公式(9)对矩阵E进行重塑，得到加密后的图像J。

3.4 解密流程

解密过程为加密过程的逆过程。

Step 1：使用SHA-512获取的哈希密钥代入DHIM映射中，得到解密所需的混沌序列。

Step 2：密文图像三通道分解并利用混沌序列进行正反两轮逆向非序列扩散。

Step 3：矩阵分块，并依据另一组混沌序列进行块间逆向循环移位、块间逆置乱、块内逆置乱、反向旋转翻转和索引排序。最终获得明文图像。

4 算法性能分析

本章节主要验证本文所设计的基于DHIM映射和分块置乱的彩色图像加密算法的有效性和安全性，实验在MATLABR2017a的仿真环境中，采用图像处理常用的标准测试图像，选取多组不同的彩色图像进行测试。按照第三章设计的加密算法，对测试图像 Lena(512×512)、baboon(512×512)、girl(768×512)进行加密、解密操作，加解密结果如图5所示。

图5 图像加解密结果

4.1 密钥空间分析

密钥空间大于100位才能保证加密算法的安全性[3]。本文提出的算法中的密钥是由512位二进制转换而成，其密钥空间大小为2512，远大于要求的2100。因此，该算法的密钥空间足够大，可以有效地抵抗暴力攻击，提高了加密的安全性。

4.2 密钥敏感性分析

高度敏感的密钥是一个加密算法的必要条件，密钥值细微改变而使得加密图像有明显变化，说明密钥敏感性强。

为了验证本文算法的密钥敏感性，实验选取fruits(512×512)作为测试图像。随机改变一个密钥值K0的小数点后第8位的数值，得到两个密钥值K1(K0+0.00000001)、K2(K0-0.00000001)， 分 别 用K1对明文加密，用K2对K0加密后的图像进行解密操作。加解密结果如图6所示：

图6 不同密钥值的加密、解密

从图6中(b)和(c)的加密效果可以看出采用不同的密钥值进行加密，得到的加密图像有明显区别；从(d)和(e)中可以看出用错误的密钥值解密无法得到明文图像。由此说明本文算法的密钥敏感性较强。

4.3 直方图分析

直方图反映了图像像素的分布，是衡量加密算法性能的重要指标。本文算法采用非序列扩散方法，将目标像素点周围的像素值与混沌序列值进行模运算，改变置乱后矩阵的像素值，使密文图像直方图的像素分布均匀，具有较强的抗统计攻击能力。

选取peppers(512×512)作为实验对象，图 7展示了加密前后三个通道的直方图对比。从图中可以看出加密后的直方图与明文图像相比，像素值分布更为均匀，可有效抵抗统计攻击。

图7 加密前后peppers的三通道直方图

4.4 相邻像素相关性分析

明文图像的相邻像素间具有较强的相关性，加密算法若不能有效降低其水平、垂直和对角线方向的相关性则会更易受到统计攻击。本文采用跨平面块间置乱和块内置乱的方法，有效降低了像素间的相关性。

为了验证本文算法的安全性，以Lena(512×512)为例随机选择3000对像素点及其加密后图像的水平方向、垂直方向和对角线方向上相邻像素对进行相关性分析并对比了其他算法的相关性。如表2所示，加密后的像素点相关性趋近于0，表明本文提出的加密算法可以有效去除相邻像素间的相关性。

表2 不同算法的Lena相邻像素相关性

4.5 差分攻击分析

差分攻击是另一种安全攻击方式，通过两个差异较小的明文进行二次加密得到密文，从两次加密后的密文关系建立起明文与密文之间的关系从而破解密文。

差分攻击是另一种测试加密算法质量的常用的攻击手段。主要是通过改变明文图像的像素值，并对其进行加密，然后通过与原始图像加密后密文进行比较，从而攻击加密算法。为了验证加密算法的抗差分攻击能力，选择Lena(512×512)、house(512×512)、airplane(512×512)作为实验对象，并用像素数变化率(NPCR)和统一平均变化强度(UACI)作为评价指标。理论上NPCR的值应大于99.6094%，且数值越大越好；UACI的理论值为33.4635%，数值越接近加密效果越好[5]。其计算方法见公式(9)和公式(10)：

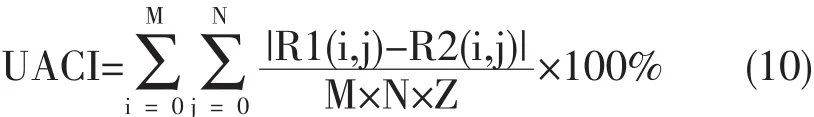
其中，M×N表示一个平面的大小，R1和R2表示仅改变一个像素点两次加密的图像，V(i,j)表示两次加密的密文图像像素不同的个数，Z表示最大允许的像素值。

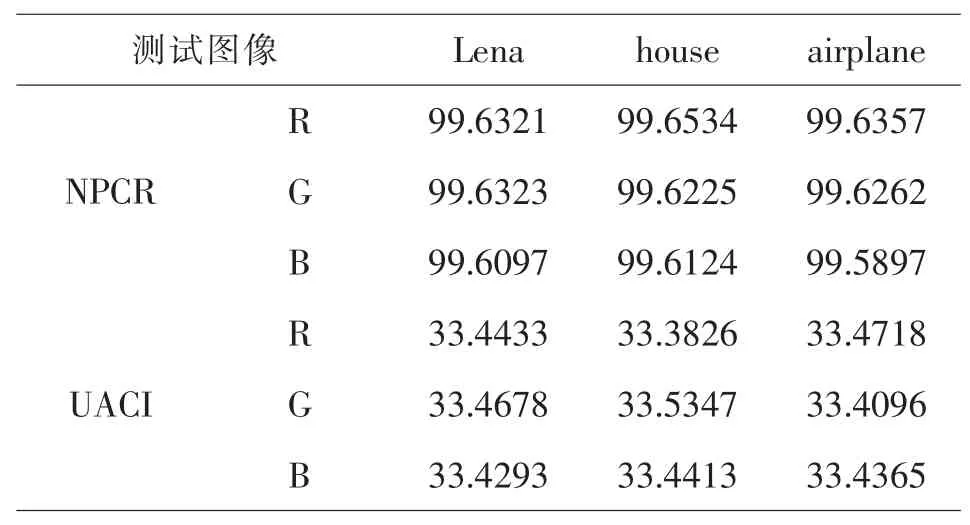
表3 NPCR和UACI的统计值

4.6 信息熵分析

信息熵是分析图像信息的随机性指标，加密后的图像信息熵越高，表示像素随机性越好。密文图像的信息熵越接近于8，说明加密算法对明文图像的加密效果越好[4]，信息熵的计算方法如公式(11)所示。

其中，a表示灰度值随机变量，N代表图像的灰度，P(ai)表示灰度值出现的概率。以Lena(512×512)作为实验对象，将本文加密算法于其他三种算法的信息熵进行比较，如表4所示。

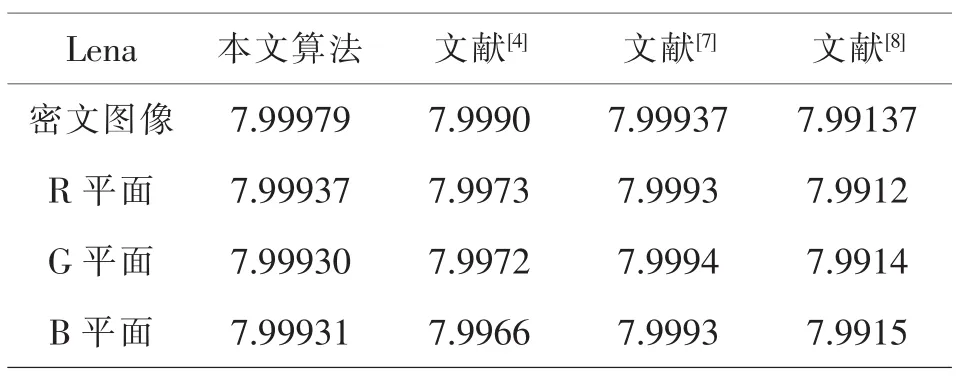
表4 不同算法Lena的信息熵

5 结束语

通过研究现有的混沌映射和彩色图像加密算法的优缺点，本文提出了一种基于动态二维映射和分块置乱的彩色图像加密算法。该算法主要利用设计的动态Henon-Iterative映射生成的混沌序列，结合块间-块内-块间置乱和两轮非序列扩散对彩色图像进行加密。通过仿真实验和安全性分析，证明本文提出的图像加密算法具有较好的安全性和鲁棒性。

在实际应用中，并不是明文图像中所有内容都是需要加密的。为了节省资源，提高算法的加密效率，在接下来的研究中，将继续利用分块的方法，结合目标检测的技术提高算法的运行效率，节省资源开销。