矢量数据多尺度表达图谱认知理论与计算
2022-09-01刘艳霞陈明建秦万英
宗 琴,刘艳霞,陈明建,秦万英
(1. 重庆建筑工程职业学院,重庆 400000;2. 武汉市测绘研究院,湖北 武汉 430072)
在地理空间数据呈几何级数增长中,出现了较为突出的两个问题。一是对于地理空间数据的存储管理而言,各行业部门在开展国家空间数据基础设施建设工作时,由于对地理空间数据的应用要求不同,导致在数据结构、数学基础、空间尺度、空间参考、语义以及几何位置等方面存在不一致;二是尽管国家投入了一定经费加强建设数据共享机制;但仍出现了地理空间数据生产随机性大、数据更新和共享管理机制不健全等问题。因此,如何对海量、多源、异构的地理空间数据进行管理、分析和更新成为当下相关科研机构、管理部门着重研究的课题[1-14]。
1 矢量信息图谱
1)矢量信息的“图”特征,是指描述地理空间实体的轮廓线条表征出的形态、大小、面积、轮廓、结构等,相比遥感信息的“图”特征,矢量信息的“图”特征更适应多尺度表达,因为其不会随着尺度变化而失真。目前自动综合技术对多尺度空间数据表达的限制使得矢量信息无法实现连续化表示,但“图特征”可以实现以其抽象、简洁、形象的符号离散化地表示地理信息。
2)矢量信息的“谱”特征,是指矢量数据表征出的类别、方向、关系、规律、变化等,相比遥感信息的“谱”特征,矢量信息虽没有光谱维信息,但其随尺度变化表现出的谱系更易量化。“图特征”实现了离散化表示地理信息,“谱特征”则完成了连续化表示,以运动、系列的谱系定量表示地理信息。
综上所述,矢量数据和遥感影像作为空间数据的组成部分,也具备了“图”和“谱”的综合信息,兼有“图形”与“谱相”的双重特性。矢量数据图谱合一的特性是多尺度表达的结果,反映了地理空间实体的地理属性,谱写了地理空间实体在空间分布、时间推移、尺度变化上的表现,是进行地理信息认知的起点和立足点[2,15-16]。
2 矢量信息图谱特性
矢量信息图谱的目标对象是地理空间实体,如同知识图谱本质上揭示实体之间关系一样,矢量信息图谱本质上具有目标的动态性、目标的相似性、关系的细粒度分析等3 个方面的特性,基于这3 个方面的特性,矢量信息图谱揭示着地理空间实体的关系,得以实现从理论上认知矢量数据的多尺度表达。
1)目标的动态性:指矢量信息图谱自动识别出同类事物,即某地理空间实体形态发生变化后,自动识别出它变化后的形态信息。
2)目标的相似性:指目标对象在不同尺度上的综合相似性。地理空间实体表达为计算机世界的空间数据后,连续尺度表达下的“图”特征和“谱”特征存在局部差异,但综合来看是相似的,这也验证了朱阿兴[17]等提出的地理相似性是地理学的第三定律。
3)关系的细粒度分析:地理空间实体因为实体类型不同表现出多样化,实体之间的关系也可能存在细粒度的不同,即要素级、目标级和几何特征级等不同层次的粒度,要素级的粒度最粗,几何特征级的粒度最精细,矢量信息图谱可以呈现出精细的实体关系。
3 矢量数据多尺度表达图谱认知理论与计算
矢量数据多尺度表达由地理信息自动综合技术实现,但目前自动化综合技术还处于理论研究阶段,真正的全智能化全自动化综合技术实时提取任意尺度表达的数据尚处于发展研究阶段。如若完成矢量数据多尺度表达图谱认知理论和计算方法论,多尺度空间数据库相关问题必将迈上新的台阶。下文将从“由图抽谱”、“图旧谱新”和“相谱相成”3 个阶段对认知理论进行论述。
3.1 由图抽谱
矢量数据的图形特征因实体对象的维度不同而有不同的描述方法。对于点实体而言,描述点实体的空间数据仅仅是单一的坐标,无法构成图形,常常将其升维为面群进行描述;对于线实体而言,描述线实体的空间数据是一系列坐标串,往往把首尾起止点连接形成封闭的面实体进行描述。基于这样的升维思想,矢量数据的图形特征更多的是面实体的几何特征。常见的特征包括面积、周长、内角、Feret直径、面积周长比率等。大部分学者专研于这些特征的描述方法,较有成效的包括形状中心点位置法、凸包法、包围盒法、重心射线法、重叠面积法、离散几何矩法、方位编码法和相对参数法等。这些描述方法更多地服务于实体之间的匹配,以实现数据更新、变化检测、数据融合等方面的应用,而挖掘图形特征中描述矢量数据发展规律的谱特征则是由图抽谱的智能化目的。
3.1.1 面实体图特征
面状实体的轮廓可以看作一系列轮廓点沿着指定的方向(顺时针或者逆时针)首尾相连形成的。已知某面状实体A的形状轮廓表示构成轮廓的轮廓点,n表示轮廓点的数量,每个轮廓点P'(i)的坐标为如图1所示。
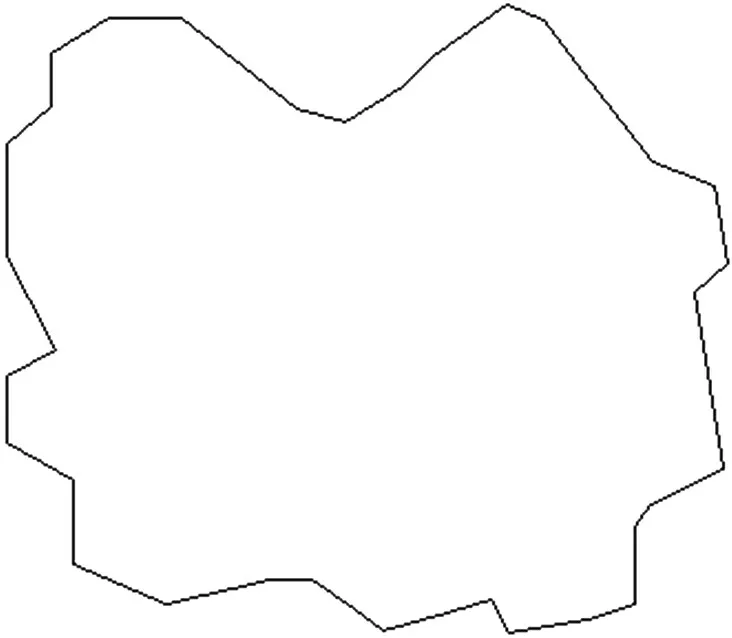
图1 面状矢量数据轮廓点提取
有了轮廓点的概念,相邻2个轮廓点则构成轮廓线段,轮廓线段再由有序的点相连成面实体形状轮廓。已知n个轮廓点P'(i)(i∈[1,n]) 组成的面实体形状轮廓S',以每对相邻的2个轮廓点P'(i)与P'(i+1) 构成一个轮廓段l'(i),则此时的形状轮廓可表示为S'={l'(i)|i∈[1 ,n] },l'(i)表示第i个轮廓段,n表示轮廓段的数量。
构成一个面实体形状轮廓的轮廓点数量往往比较多,因此利用等间隔采样的方法采样轮廓点从而简化计算过程,得到采样后的轮廓点集合S={P(i)|i∈[1 ,m] },P(i)为重采样后的轮廓点;m为重采样后的轮廓点数量。图2 表示重采样后的面状实体,可见适当的采样频率能够在减少轮廓点数量的同时保留形状细节,所以形状轮廓可以表示为S={l(i)|i∈[1 ,m] },l(i)为由重采样后的轮廓点构成的轮廓段(图2)。
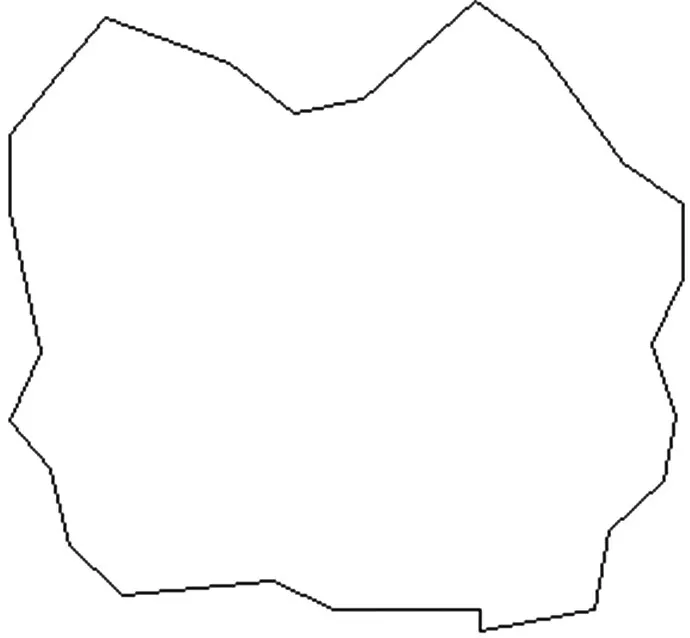
图2 重采样后的面状矢量数据
按照参考文献[18]针对栅格数据模型的提取策略,提取面实体的图特征,提出如表1 所示的图特征要素。本文将轮廓距离定义为从形状轮廓段的起点沿着轮廓,到另一端点所经过的轮廓长度为轮廓段的轮廓距离。轮廓段lk(i)两端点P(i)和p(i+ak)的轮廓距离codk(i):从起点P(i)到终点p(i+ak)沿着轮廓经过的所有轮廓点,每对相邻接轮廓点的欧氏距离之为:
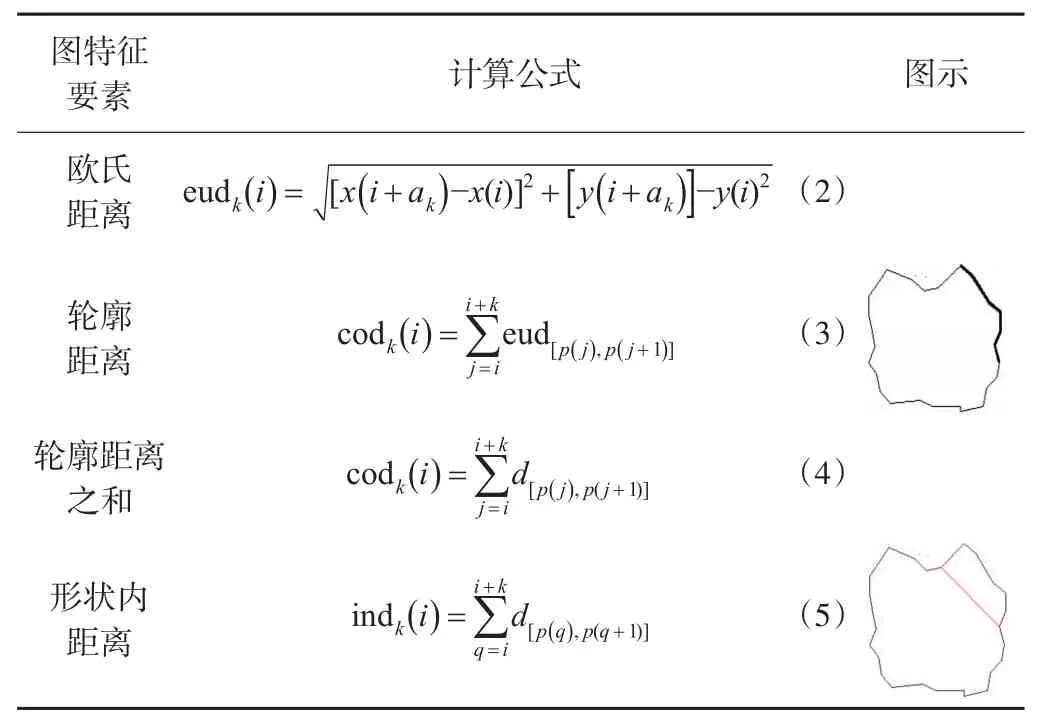
表1 面实体图特征要素
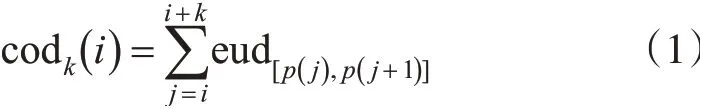
式中,p(j)∈C(i);C(i)为轮廓段lk(i)从起点P(i)到终点p(i+ak)构成轮廓路径的轮廓点集合。
3.1.2 面实体谱特征抽取
由面实体的图特征抽取面实体的谱特征,组成参数包括3.1.1 中的欧氏距离、轮廓距离、轮廓距离之和与形状内距离。抽取的谱特征包括归一化形状内距离、形状内距离变化率、归一化形状内距离与轮廓距离的比值、归一化欧氏距离与形状内距离的比值、归一化欧氏式距离与轮廓距离的比值(如表2)。

表2 面状实体谱特征
抽取如表2所示的面实体谱特征,即:

式中,k表示当前尺度层序数;K为尺度的总层数;这里选择6个尺度及K=6
3.1.3 面实体谱特征尺度化
采样后的面实体有m个轮廓点,轮廓段lk(i)表示从起点p(i) 按逆时针方向以间隔ak个轮廓点的p(i+ak)为终点构成的轮廓段,其中:

式中,k为当前尺度层序数,以6 个尺度为例,那么采样后的轮廓点p(i)为起点构成的多尺度轮廓段分别为以轮廓点为终点构成的轮廓段。从公式(12)中可以看出,当K=6 时,表示最小尺度轮廓段,此时lk(i)最短,包含的形状轮廓最小,体现了实体的局部特征;当K=1 时,表示最大尺度轮廓段,此时lk(i)最长,即第一层尺度时表示轮廓段最长,包含了面实体的半全局特征。
这样,对于采样后的实体,每个轮廓点在每个尺度上都有5类特征参数,即每个轮廓点p(i)都有5×K个特征参数,分别代表了以p(i)轮廓点为起点的面实体的局部细节与全局整体特征。
3.2 图旧谱新
矢量数据多尺度表达,常规的表达思维是根据不同的应用存储静态的不同尺度的数据版本,或者存储精细的数据版本再根据应用进行动态综合,尚未实现真正意义上的全自动表达。实际上构成矢量数据的主要空间实体面实体,其形态的变化规律如果组建图谱,那么多尺度表达便可开辟新的路径。
面实体在当前尺度下的图特征本身是静态化的属性,而当前尺度下的谱特征可以动态化,从而预测下一个尺度的图特征(这一构建思想在早期的研究中已有说明)。设当前尺度为N,面实体A、B、C分别为尺度N,N-1,N+1 下的面实体,其轮廓点为pi和qj与rk,两实体之间的距离函数定义为d(pi,qj)和d(pi,rk),即:
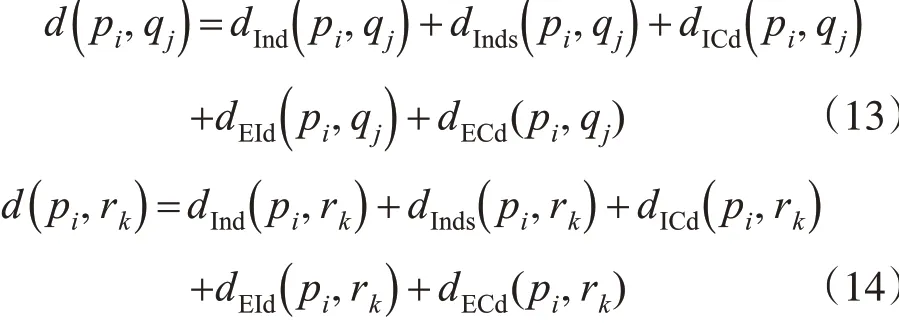
其中:
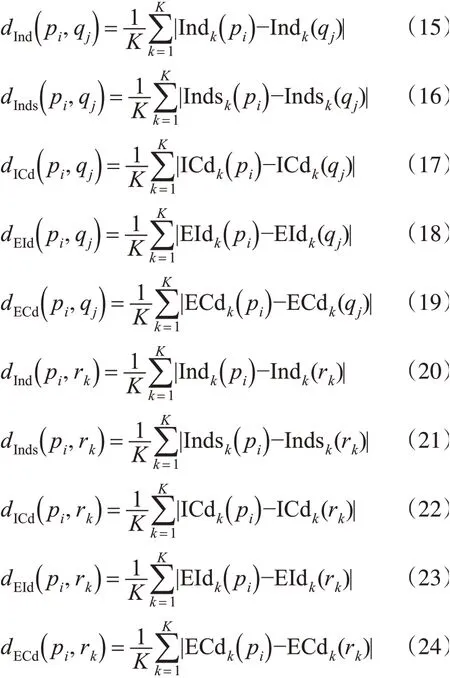
为了推算尺度N+1 下的面实体C 的轮廓点特征,以面实体A 轮廓点的特征序列为行向量,以面实体B轮廓点的特征序列为列向量,利用前面定义的距离函数构成距离矩阵。
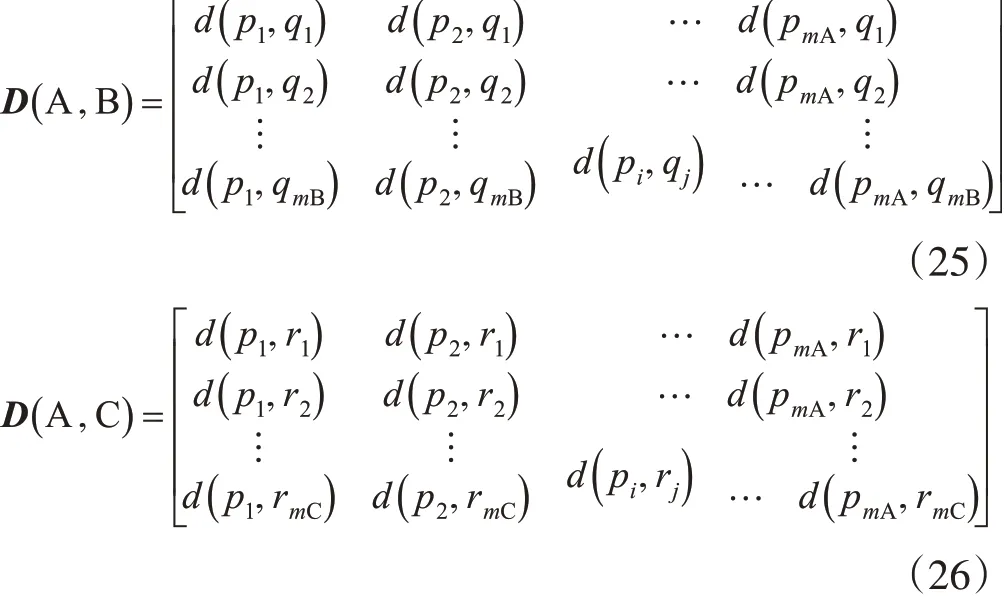
通过计算尺度N和尺度N-1 下的距离矩阵,以及尺度N-1和尺度N-2 下的距离矩阵,发现距离矩阵变化规律,从而推算尺度N和尺度N+1 下的距离矩阵,由此反演尺度N+1 下的C 实体的轮廓点及其图特征。
4 结 论
在大数据时代,地理信息的飞速增长使得现势数据呈现堆积的状态,随之出现的数据融合、联动更新、变化检测方面的问题限制了矢量数据的及时应用。本文对矢量数据多尺度表达图谱理论进行了论述,从根源上剖析地理空间实体认知规律,为大数据背景下的地理信息研究提供相应的参考。
