基于比例谐振与重复控制的400 Hz中频逆变器控制研究

王晓雷， 李志恒， 郭飞亚， 石金飞， 吕豫阳， 左松伟

(中原工学院 电子信息学院， 河南 郑州 450007)

广泛应用于航空航天、船舶、武器装备等领域的400 Hz中频电源，具有高质量的输出电压波形、精准的控制精度、良好的动态性能和稳态性能。在不考虑逆变器拓扑结构时，对逆变器控制策略的研究一直是相关领域学者关注的焦点。在诸多控制策略中，比例积分(Proportional Integral，PI)控制是目前使用最为广泛的。它算法简单，参数易设计，但针对交流量的跟踪存在静差问题，控制效果不佳。基于单相坐标变换进行交流信号提取的闭环解耦控制策略[1]，可实现无静差跟踪，但谐波抑制能力很弱。用比例谐振(Proportional Resonant，PR)控制器设计多个频率的谐振腔来抑制输出波形畸变时，谐振环节参数设计的工作量较大，控制系统的结构较复杂，不利于400 Hz中频逆变器的实际应用[2-3]。基于内模原理的重复控制方式可以有效地抑制波形畸变，被广泛应用于400 Hz中频逆变器的输出控制。然而，当负载变化时，重复控制的方法在动态性能上表现较差。

为了提高输出波形的电能质量，不少学者对基于重复控制的复合控制策略进行了研究，如：文献[4-5]将重复控制方式和PI控制方式结合起来，应用到逆变器的控制中，虽然使控制精度和动态性能显著提高，但所用复合控制策略的谐波抑制能力易受PI参数的影响，相应的控制器设计比较复杂；文献[6]利用比例控制和重复控制并联的结构实现了较快的动态响应，但控制精度不高；文献[7-8]提出的由重复控制与准比例谐振控制相结合的复合控制策略，兼具准比例谐振控制器和重复控制器的优点，控制精度较高，能让系统的抗干扰性及其动态性能大幅度提升，但并没有给出详细的参数设计方法。本文针对400 Hz中频电源的电能质量进行系统建模和实验，讨论基于比例谐振与重复控制的复合控制策略，并对控制器参数进行设计。

1 400 Hz中频逆变器介绍

针对基于比例谐振与重复控制的复合控制策略，可设计图1所示复合控制的400 Hz中频逆变器电路框图。在逆变单元中，4个开关元件VT1-VT4与续流二极管反并联，构成电压型逆变桥式电路，电感器(其电感为L)和电容器(其电容为C)组成电感电容滤波器。

注：udc、ui、uo分别为直流母线电压、逆变桥臂侧电压和输出电压；uref为给定的输出电压参考值；iL 、iC、io分别为电感器电流、电容器电流和输出电流；R为逆变器电路的等效电阻；Ro为负载电阻。图1 所设计复合控制的400 Hz中频逆变器电路框图Fig. 1 Circuit block diagram of 400 Hz intermediate frequency inverter based on compound control

根据图1中电压型逆变桥式电路，可列出系统空载时被控对象的传递函数，即

(1)

式中：Uo(s)、Ui(s)分别为uo、ui的拉普拉斯变换后形式；s为拉普拉斯算子。

本文根据文献[9]设定的400 Hz中频逆变器参数如表1所示。

表1 400 Hz中频逆变器参数Tab. 1 System parameters of 400 Hz intermediate frequency inverter

2 复合控制理论分析

本文将比例谐振控制器与重复控制器并联，组成了图2所示的复合控制结构。

图2 复合控制的结构Fig. 2 Structure diagram of compound control strategy

图2中：z为单位超前因子，在频域内z=ejω，角频率ω∈(0,π/Ta)；r(z)为指令信号；GPR(z)为比例谐振控制器的离散传递函数；e(z)为误差信号；Q(z)为内模滤波器；z-N为让控制系统相位超前的调节函数的必要组成部分，它使得逆变器能延迟一个周期输出；C(z)为补偿环节；P(z)为P(s)离散后的传递函数；u(z)和d(z)分别为控制器的输出量和扰动量。

重复控制器主要由内模和补偿环节两大部分组成。其内模可表示为z-N/(1-Q(z)z-N)，能对误差信号e(z)进行逐周期积分，当内模滤波器Q(z)=1时，可实现对指令信号r(z)的无静差跟踪。其补偿环节C(z)=kRzkS(z)，可提供幅值补偿和相位补偿。其中比例增益kR为幅值补偿的关键参数；zk为超前环节；k为超前环节系数，可以补偿被控对象和滤波器在相频上的滞后；补偿器S(z)一般为低通滤波器和陷波器的组合，主要用于将被控对象的中低频段增益校正为1，使其高频段迅速衰减，从而减小重复控制器的设计难度，提高控制系统的稳定性和抗干扰能力。当系统稳定时，复合控制器的误差信号为：

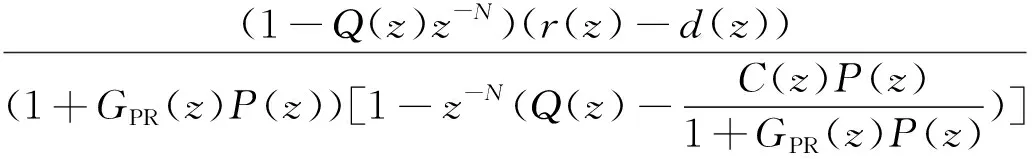
(2)

令新的被控对象Po(z)=P(z)/(1+GPR(z)P(z)),且H1(z)=1+GPR(z)P(z),H2(z)=1-z-N(Q(z)-C(z)Po(z))，则控制系统的特征值多项式为：

H(z)=H1(z)H2(z)

(3)

要让系统稳定，需式(3)满足H1(z)=0和H2(z)=0的特征根都位于单位圆内的条件。当逆变器单独采用PR控制器时，其闭环控制系统的特征值多项式为H1(z)，此时系统若保持稳定，可满足H1(z)=0的特征根位于单位圆内这一条件。当逆变器单独采用重复控制器时，其闭环控制系统的特征值多项式为H2(z)。欲使H2(z)=0的特征根也在单位圆内，就应将系统等效为重复控制器作用下的稳定状态。

当重复控制器单独作用于被控对象Po(z)时，闭环控制系统的特征方程为：

1-z-N(Q(z)-C(z)Po(z))=0

(4)

系统稳定时，有

|z-N(Q(z)-C(z)Po(z))|<1

(5)

当逆变器输出电压频率为基频及基频的整数倍时，易知|z-N|=1。由此可推导出系统稳定的条件,即：

(6)

3 复合控制器设计

3.1 比例谐振控制器设计

在复合控制器设计中，必须保证其PR控制器的稳定。PR控制器的传递函数为：

(7)

式中：KP、KR分别为比例系数和谐振控制系数；ωR为谐振角频率。

采用零阶保持器(Zero-order Holder，ZOH)离散法时，对应于GPR(s)的离散传递函数为：

(8)

在PR控制器参数设计中，因谐振控制器只对谐振点的频率产生明显影响，对其他点的频率影响较小，所以可暂时忽略谐振控制器的影响，在选取合适的比例系数KP后进行谐振控制系数KR的设计。

3.1.1 确定比例系数

当逆变器只采用比例控制方式时，根据式(1)和表1参数，可求出开环控制系统的离散传递函数，即

(9)

根据式(9)，可画出图3所示比例控制器作用下控制系统的根轨迹。其中，系统增益为无量纲量。

由图3可知，对于稳定的控制系统，KP的取值范围是[0，0.126]。为保证系统的稳定裕量，通常要求控制系统在频域内相位裕量大于或等于60°，幅值裕量大于或等于6 dB。取KP=0.05，可得图4所示比例控制器作用下控制系统的伯德图。该参数下，幅值裕量为8.07 dB，相位裕量为无穷大。

图4 比例控制器作用下控制系统的伯德图Fig. 4 Bode diagram of control system with proportional action

3.1.2 确定谐振控制系数

对于谐振控制器来说，其谐振点的位置变化会引起控制系统在相频响应上有±90°的相位跳变，导致在频域内分析控制系统稳定性的过程更为复杂。因此，设计时应根据已知的比例系数，在画出KR的根轨迹后，求取满足系统稳定要求的KR值范围。

在逆变器单独使用PR控制方式时，闭环控制系统的特征方程为：

(10)

根据参数根轨迹的定义，可将该控制系统等效为单位反馈系统。等效后系统的开环传递函数为：

(11)

将有关量和表1的逆变器参数值代入式(11)，可推导出对应于B(s)的离散传递函数，即

(12)

根据式(12)，可画出图5所示KR变化时控制系统的根轨迹。

图5 KR变化时控制系统的根轨迹Fig. 5 The root locus of the control system when the KR changes

由图5可知，KR的取值范围是[0，8 590]，但具体取值仍需进一步分析确定。图6所示为KR为1 000、2 000、3 000时控制系统的伯德图。

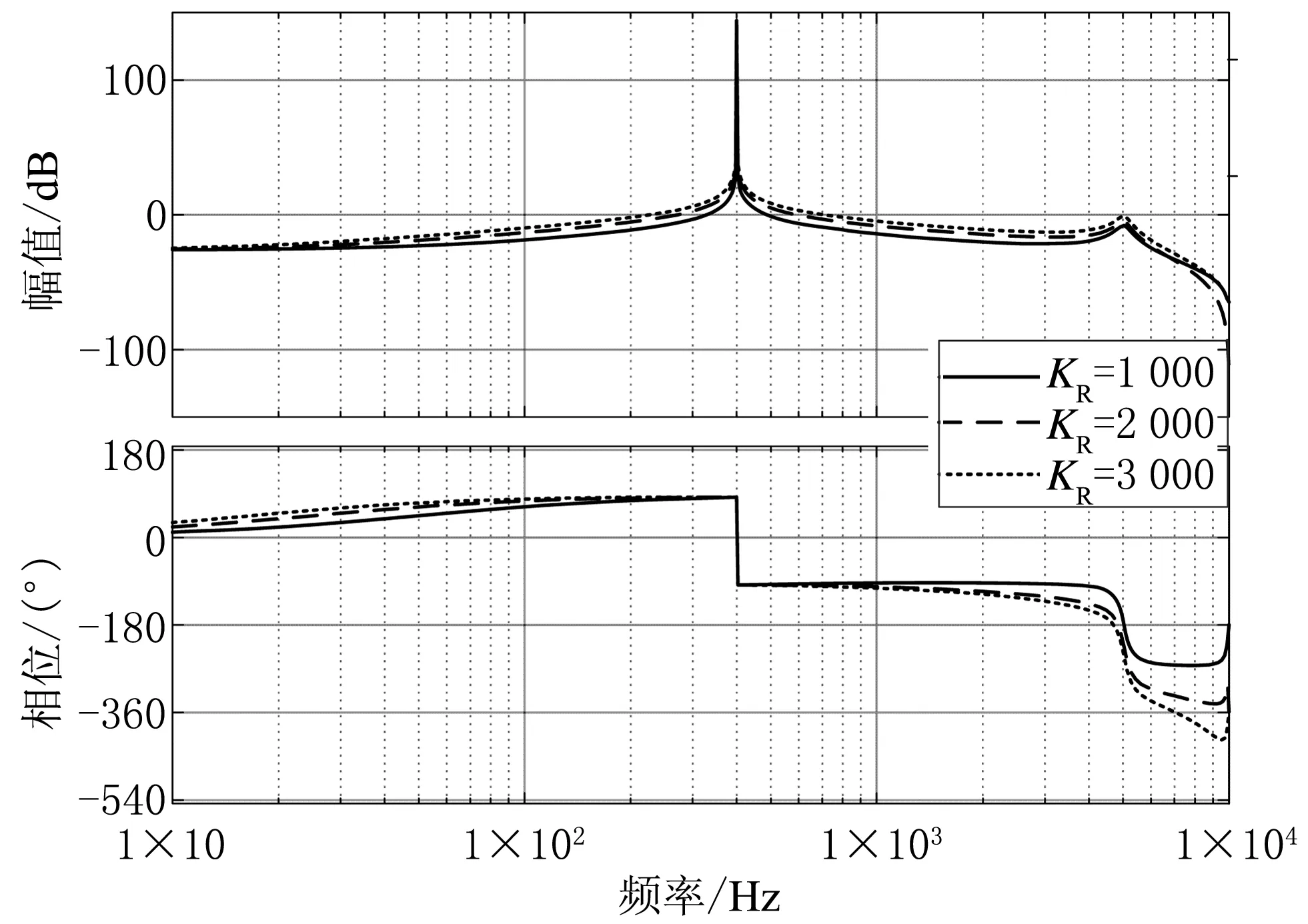
图6 KR为1 000、2 000、3 000时控制系统的伯德图Fig. 6 Bode diagrams of control systems when KR is 1 0000,2 000,3 000

由图6可知，KR取值越大，控制系统响应越快，但稳定性越差，其电感电容滤波器截止频率处的谐振峰也越大[10]。考虑到实际控制中可能存在的延时和电感电容参数的不确定性，本文取KR=2 000，以兼顾系统稳定性和响应速度的要求，并使控制系统具有较好的鲁棒性。

3.2 重复控制器设计

在设计重复控制器时，被控对象仍为Po(z)。依据重复控制的定义，其参数设计主要包括内模滤波器Q(z)、补偿器S(z)、超前环节系数k以及比例增益kR。

3.2.1 确定内模滤波器Q(z)

Q(z)是增强系统稳定性、实现指令信号无静差跟踪的关键参数，通常取略小于1的常数或者近似于低通滤波器的值。Q(z)越接近于1，控制系统的稳态误差越小，抑制谐波的能力越强，但同时会导致高频段的H2(ejω)轨迹出现在单位圆的外部，造成系统的不稳定。

比较而言，低通滤波器虽然能提高控制系统的稳定性，但会使控制系统丧失对中高频段谐波的抑制能力，并且会增加控制系统的设计复杂度。为简化设计，本文采用常数法，并根据文献[11]分析，取Q(z)=0.95，以增强控制系统的鲁棒性。

3.2.2 确定补偿器S(z)

(13)

被控对象Po(z)补偿前后的伯德图如图7所示。图7中，曲线a、b、c分别代表Po(z)、Po(z)S1(z)、Po(z)S1(z)S2(z)的伯德图。对比曲线a、b可知，虽然低通滤波器能在一定程度上抑制谐振峰，但是效果仍不太理想。为此，可采用零相移陷波器来消除谐振峰，且它不会破坏系统的稳定性。已知逆变器中电感电容滤波器的谐振角频率ωc≈31 623 rad/s，采样时间Ta=5×10-5s，可求得零相移陷波器，即

(14)

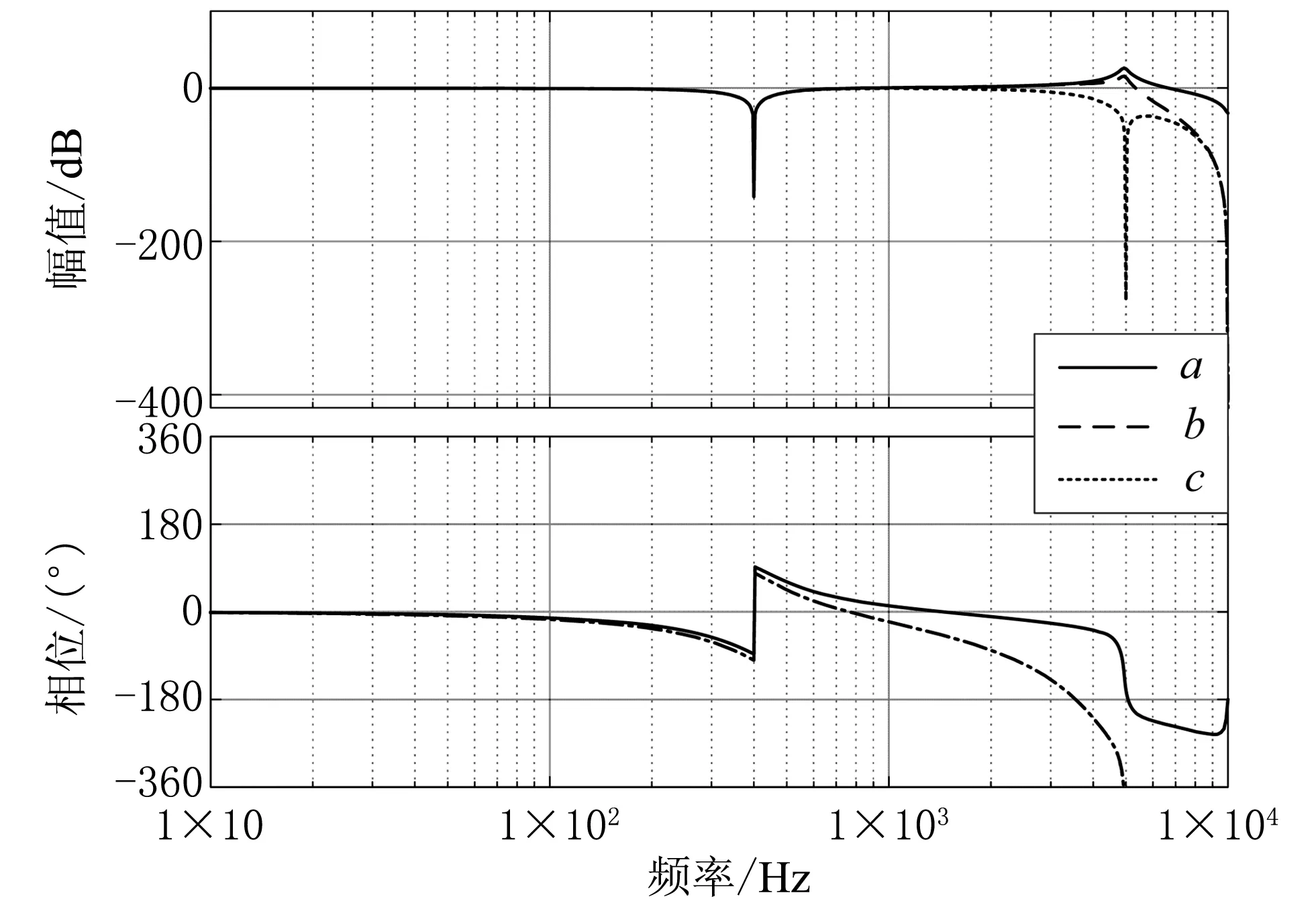
图7 被控对象Po(z)补偿前后的伯德图Fig. 7 Bode diagram of the controlled object Po(z) before and after compensation

结合图7分析可知，在陷波器的作用下，系统的谐振峰进一步得到抑制，除基频和基频附近外，控制系统在中低频段基本实现了0 dB增益的要求。

从图7可看出，在相频特性曲线中，如果不考虑基频及其附近区域的影响，则控制系统会出现明显的相移。这是由于被控对象Po(z)本身存在相位滞后，而四阶巴特沃斯滤波器会加剧这种滞后现象。显然，这不利于保持系统的稳定。

3.2.3 确定超前环节系数k

为改善控制系统的相频特性，可引入超前环节zk，因为它能够提供θ=k(ω/π)180°的相位补偿。k值为2、3、4时控制系统的相频特性曲线如图8所示。显然，选择k=3，能使控制系统在更宽频段上相位趋近于0，提供4 kHz范围内的谐波补偿能力。

图8 k值为2、3、4时控制系统的相频特性曲线Fig. 8 Phase frequency characteristic curve of control system when k is 2,3,4

3.2.4 确定比例增益kR

比例增益kR是幅值补偿的关键参数，会影响控制系统的响应速度和谐波抑制能力，且其值过大的话会造成系统的不稳定。为简化kR参数的设计过程，本文给出了图9所示kR值为0.3、0.6、0.9时H2(ejω)的轨迹。这里，H2(ejω)为重复控制器单独作用时闭环控制系统的特征值多项式。

可见现有的对RPL的改进仍存在缺陷。为解决上述问题,本文提出基于模糊层次分析法的RPL路由协议—RPL-FAHP(RPL Based on Fuzzy Analytic Hierarchy Process,RPL-FAHP)。RPL-FAHP在节点选择偏好父节点(下一跳节点)时全面综合考虑候选父节点的剩余能量、ETX、端到端时延及跳数。并构建新的复合路由度量及目标函数。同时采用模糊层次分析法[8]确定复合度量中各个路由度量的权重系数。节点根据新提出的复合路由度量和目标函数构建网络拓扑结构和选择路由,进而有效的改善网络各方面的性能。

图9 kR值为0.3、0.6、0.9时H2(ejω)的轨迹Fig. 9 H2(ejω) trajectory when kR is 0.3,0.6,0.9

从图9可看出，无论kR取何值，控制系统在基频附近都处于临界稳定的边缘，这是因为PR控制器被包含在被控对象中，但是这并不会引起系统的不稳定；随着kR值的增大，控制系统的稳定性会降低，但误差信号收敛速度会加快，抑制谐波能力也会提高。考虑到实际逆变器控制中存在的滞后现象，以及系统建模的不确定性，应保守地选择kR值，本文取kR=0.5。

4 复合控制策略的实验验证

根据上文，可确定表2所示的复合控制器参数。图10所示为重复控制和复合控制的开环幅频曲线。

表2 复合控制器参数Tab. 2 Compound controller parameters

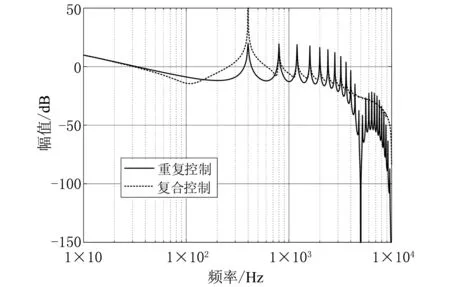
图10 重复控制和复合控制的开环幅频曲线Fig. 10 Open loop amplitude frequency curve of repetitive control and compound control

从图10可以看出，复合控制在基频处具有无穷大增益，同时在低频部分能达到与重复控制相同的谐波抑制能力，且复合控制中PR控制器的作用使其具有更好的动态响应性能。

为了验证上述复合控制理论分析以及参数设计的合理性和有效性，本文搭建了图11所示的400 Hz中频逆变器实验平台。该实验平台采用了TMS320F28335主控芯片。

图11 400 Hz中频逆变器实验平台Fig. 11 Experimental platform of 400 Hz intermediate frequency inverter

在单独的重复控制中，系统的输出静差容易受Q(z)的影响，因此实验中基波电压给定值应略高于PR控制方式和复合控制方式。逆变器空载时，PR控制、重复控制和复合控制的输出电压波形如图12所示。

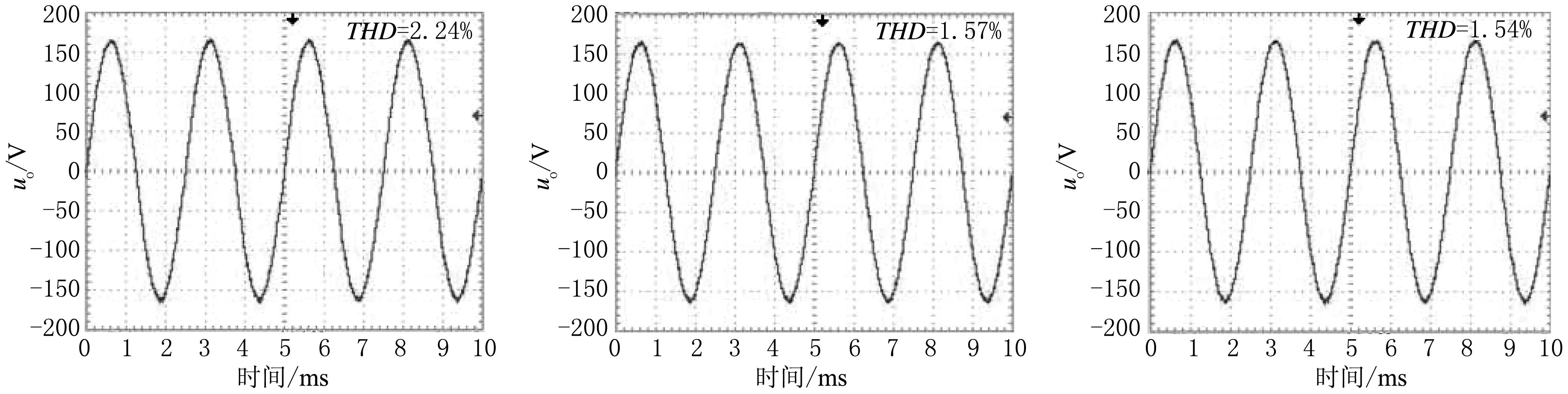
(a) PR控制方式 (b) 重复控制方式 (c) 复合控制方式图12 逆变器空载时PR控制、重复控制和复合控制的输出电压波形Fig. 12 Output voltage waveform of PR control, repetitive control and compound control under inverter no-load

从图12可知，在设计参数下，逆变器空载时复合控制的输出电压总谐波失真(Total Harmonic Distortion，THD)为1.54%，在3种控制方式中最低，达到了较好的控制效果，且具有一定的稳定性裕量。这和理论分析一致。

对逆变器施加50 Ω阻性负载时，PR控制、重复控制和复合控制的输出电压波形、电流波形、输出电压THD如图13所示。

(a) PR控制的输出电压波形、电流波形 (b) PR控制的输出电压THD

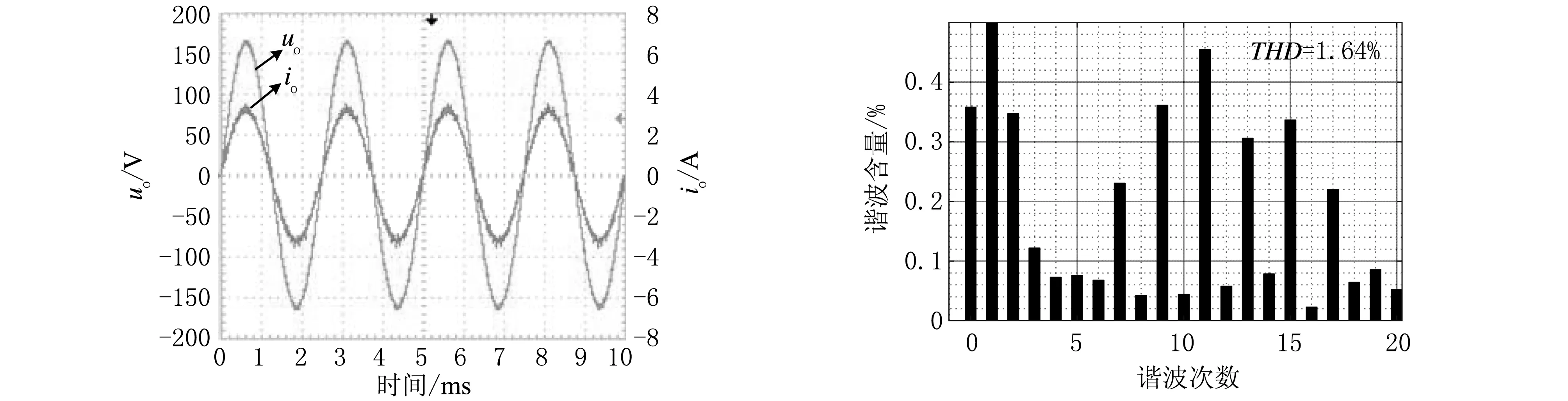
(c) 重复控制的输出电压波形、电流波形 (d) 重复控制的输出电压THD

(e) 复合控制的输出电压波形、电流波形 (f) 复合控制的输出电压THD图13 阻性负载下PR控制、重复控制和复合控制的输出电压波形、电流波形和输出电压THDFig. 13 Output voltage and current waveform and output voltage THD analysis of PR control, repetitive control and compound control under resistive load

从图13可知，阻性负载下PR控制、重复控制、复合控制的输出电压THD分别为1.87%，1.64%，1.60%。不难发现，复合控制达到了和重复控制一样的谐波抑制能力，且复合控制相对于单独重复控制来说，不受内模滤波器Q(z)的影响，兼具PR控制在基频处无穷大增益的优点。

为进一步验证复合控制方式抑制谐波的能力，本文以整流性非线性负载为对象，对3种控制方式的逆变器输出电压波形、电流波形进行了对比。所施加整流性非线性负载的直流侧滤波电容为220 μF,负载电阻为75 Ω。非线性负载下PR控制、重复控制和复合控制的输出电压波形、电流波形、输出电压THD如图14所示。

(a) PR控制输的出电压波形、电流波形 (b) PR控制的输出电压THD

(c) 重复控制的输出电压波形、电流波形 (d) 重复控制的输出电压THD

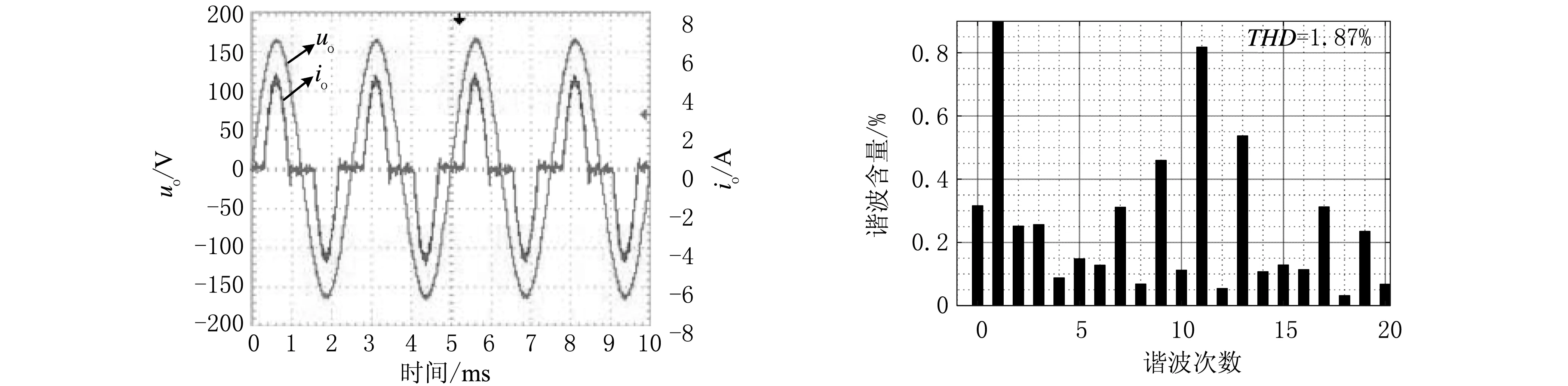
(e) 复合控制的输出电压波形、电流波形 (f) 复合控制的输出电压THD图14 非线性负载下PR控制、重复控制和复合控制的输出电压波形、电流波形和输出电压THDFig. 14 Output voltage and current waveform and output voltage THD analysis of PR control, repetitive control and compound control under nonlinear load

从图14可知：非线性负载下PR控制的输出电压THD为4.28%，而重复控制和复合控制的输出电压THD分别为1.90%和1.87%；相对于PR控制方式，重复控制和复合控制的输出电压THD分别减少了2.38个百分点和2.41个百分点，电压波形未出现明显畸变。这又一次验证了复合控制参数设计的合理性，同时证明复合控制具有与重复控制一样的波形畸变的抑制能力。

为验证复合控制的动态响应能力，本文对控制系统突加50 Ω阻性负载，对比了3种控制方式的输出电压电流动态响应波形(见图15)。对比发现，突加负载时，重复控制在瞬间有较大的电压跌落，输出电压在2～3个基波周期后才恢复正常，而PR控制和复合控制在1个基波周期内已经恢复到稳态值。这从很大程度上证明，复合控制策略具有良好的动态性能，抗扰能力较强。

(a) PR控制方式 (b) 重复控制方式 (c) 复合控制方式图15 突加负载下PR控制、重复控制和复合控制的输出电压电流动态响应波形Fig. 15 Output voltage and current dynamic response waveforms of PR control, repetitive control and compound control under sudden load

5 结语

本文设计的复合控制器采用了比例谐振控制与重复控制的并联结构。首先对复合控制器进行稳定性分析，给出了设计控制器参数的思路，然后基于单相全桥逆变器数学模型，介绍了400 Hz中频逆变系统复合控制器的参数设计过程。实验表明：复合控制策略兼具比例谐振控制和重复控制的优点，能够实现对指令信号的无静差跟踪，对负载突变有较快的响应速度，对非周期性干扰和周期性干扰都有较强的抵抗能力，且能提升波形输出质量。实验证明了所设计复合控制策略的合理性和有效性。