分布式光伏发电系统的谐波源机理模型

陈少伟，林坤杰，陈碧琳

（国网福建省漳州供电有限公司，福建 漳州 363000）

0 引言

随着大量分布式光伏发电系统（以下简称“光伏电源”）的并网，光伏电源作为一种谐波源向配电网注入大量谐波电流，严重影响了配电网的正常运行。因此，必须分析光伏电源的谐波特性，建立其谐波源模型，从而为谐波责任分摊提供理论依据［1-3］。传统的谐波源模型表征的是电弧炉、中频炉等非线性负荷的谐波发射特性，主要分为恒流源模型［4-6］、诺顿等效模型［7-10］及耦合导纳矩阵模型［11-14］。由于光伏电源与非线性负荷的谐波特性存在较大的差异，且光伏电源的发电功率存在明显的波动性与不确定性，因此现有的谐波源模型不能很好地表征其谐波特性。文献［15］分析了光伏电站谐波产生原理，计算不同工况下光伏电站输出的谐波电流，建立光伏电站动态谐波域模型，但该模型忽略了功率波动对谐波特性的影响，较难应用于光伏电源。文献［16］分析了电网参数与控制参数对分布式光伏发电谐波特性的影响，建立了电压源型逆变器的受控源等效电路模型。然而，目前鲜有文献考虑光伏电源发电功率对谐波特性的影响，难以解决功率不确定性与波动性所带来的谐波发射水平不确定的问题。故本文从机理建模的角度出发，提出一种考虑光伏电源发电功率不确定性与波动性的谐波源模型。基于光伏电源的并网控制策略，结合逆变器的谐波产生原理，分析了光伏电源发电功率与逆变器调制信号幅值的机理关系，推导出发电功率与注入电网的谐波电流的函数关系式，从而解决光伏电源谐波发射水平的不确定性。采用PSCAD搭建分布式光伏电源的仿真模型，以验证该谐波源机理模型的合理性。

1 光伏电源的工作原理

光伏电源由发电机组、逆变器、控制器、滤波器四部分构成［17-18］，图1为光伏电源的结构。发电机组将光能转化为直流电能，由于光能的不确定性导致发电机组输出功率的不确定性。光伏电源的发电机组采用的是最大功率控制策略，通过调节光伏组件的直流输出电压，使其能在各种不同的光照、温度下输出最大的发电功率。逆变器在最大发电功率已知的情况下，将直流电逆变成幅值和相角满足并网要求的交流电，但同时也会产生相应的谐波分量。滤波器由电感和电容组成，可以过滤掉部分谐波电流。由于光伏电源的逆变器并网是谐波产生的根本原因，故分析逆变器谐波产生的原因是谐波源机理建模的基础。

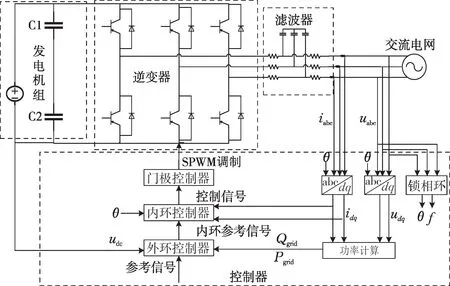
图1 光伏电源结构

2 逆变器的谐波产生机理

2.1 逆变器的工作原理分析

图2为三相逆变器等效电路，其中逆变器采用半桥式的拓扑结构，由6 个全控型开关器件组成。其基本的工作原理为：以直流电源中点O 为参考零电位，控制同一桥臂的上、下两个开关阀互补通、断。当A 相上桥臂T1导通，下桥臂T4截止时，节点A 输出电压为Vdc/2；当下桥臂T4导通，上桥臂T1截止时，节点A 输出电压为-Vdc/2，同理B 和C 点根据上、下桥臂的导通情况决定其电压。因此，三相输出的电压vAO、vBO、vCO为以导通时间为宽度，幅值为±Vdc/2的脉冲波形。

图2 三相逆变器等效电路

目前，逆变器一般选用双极性SPWM（正弦脉冲宽度调制）控制算法来控制阀的通断时间，双极性SPWM控制算法不仅能有效地控制逆变器输出的电压满足并网要求，并且产生的谐波电压畸变率在其他同类算法中最小［20］。

2.2 逆变器谐波数学分析

采用双重傅里叶积分函数分解输出的脉冲电压vAO的波形得［21］：

式中：Vrm为调制信号var的幅值；Vdc/2 为逆变器输出的直流电压幅值；ωr为调制信号var的角速度；θr为调制信号var的初始角；ωc为载波信号vc的角速度；θc为载波信号Vc的初始角。

Jn为第一类贝赛尔函数，其表达式为：

分析式（1）可得：输出电压vAO由基波电压分量、奇数倍载波频率的谐波分量和以载波倍频为中心展开的边带谐波分量3部分构成。这3部分分量的频率f可以表示为：

式中：m为非负整数，n为整数，但不为0。逆变器产生的谐波电压分量的幅值受调制信号幅值Vrm的影响。

3 控制器控制算法原理分析

鉴于光伏电源发电的不确定性，一般采用恒功率控制策略［22-23］。恒功率控制策略的实质为在追求能源利用效率最高的情况下，控制光伏电源在较短的时间内借助控制器算法控制逆变器输出给定的功率。因此，通过分析恒功率控制策略与逆变器调制信号幅值的关系，建立光伏电源发电功率与调制信号幅值的函数关系式。

3.1 外环控制器控制算法原理分析

控制器由外环控制器和内环控制器构成，外环控制器根据控制策略输出电流信号，内环控制器根据电流信号生成调制信号的幅值Vrm。图3 为恒功率外环控制器的原理图，其工作原理为：通过计算光伏电源并网的实际功率与给定的恒定功率差值，借助PI 算法进行负反馈调节，以生成电流信号，使其最终输出的实际功率为恒定功率。

图3 恒功率外环控制器原理图

其步骤为：

1）测量光伏发电并网处的三相瞬时电流iabc和三相瞬时电压uabc，将其派克变换为id、iq、ud、uq，设置d轴与电压矢量ua同方向，则uq为0，光伏电源输出的功率表达式为：

式中：Pgrid和Qgrid分别为光伏电源发出的有功功率、无功功率。

2）将有功功率Pgrid和无功功率Qgrid经过低通滤波器得到基波有功功率Pfilt和基波无功功率Qfilt。

3）将Pfilt和Qfilt与控制策略给定有功信号Pref和无功信号Qref进行比较，借助PI算法，将两者的误差生成电流控制信号idref和iqref，送入内环控制器，进一步处理。

3.2 内环控制器控制算法原理分析

内环控制器的基本原理为：通过处理电流信号和并网点的电压信号，生成逆变器的调制信号，从而控制逆变器输出给定的功率。

图4为内环控制器的原理图，其内环控制器控制算法的步骤为：

图4 内环控制器原理图

1）将三相瞬时值电流iabc经过派克变换到id和iq，并经过低通滤波器得到idfilt和iqfilt。

2）idfilt和iqfilt与将外环控制器生成的电流信号idref和iqref进行比较，将误差进行PI 控制，设置电压前馈补偿和交叉耦合补偿的参数从而得到uL1d和uL1q。借助模值限制器，将uL1d和uL1q转化成调制信号Pmd和Pmq。

3）将调制信号进行反派克变换得到调制信号Pma、Pmb和Pmc，将调制信号送入逆变器，从而控制逆变器输出给定的基波电压。

3.3 调制信号幅值与功率的函数关系

由于光伏电源最终输出控制策略给定的有功信号Pref和无功信号Qref，通过外环控制器处理生成电流控制信号idref和iqref，因此，光伏电源稳定运行时，外环控制器输出电流信号的表达式为：

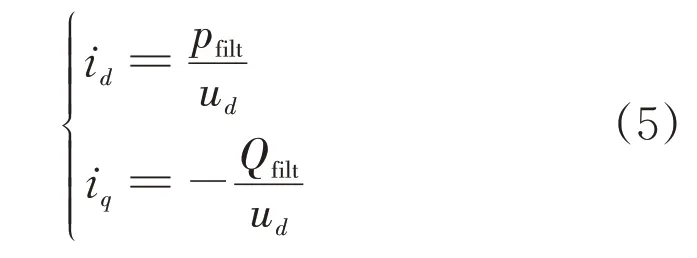
由于内环控制器的控制参数受滤波器内部电路参数的影响，因此必须分析其内部电路参数与电流信号的关系，从而建立电流信号与逆变器调制信号的函数关系。图5 为光伏电源并网的原理图，逆变器输出的电压为Ush；uLa、uLb、uLc为逆变器输出的基波电压；P1和Q1分别为逆变器输出的基波有功功率和无功功率，其中LC滤波器，其电感参数为L1，电容参数为C，由于逆变器输出的电压经L1、C并网，为了更好地分析其电路关系，分别建立L1、C的状态方程，则电感L1的状态方程为：

图5 光伏电源并网原理图

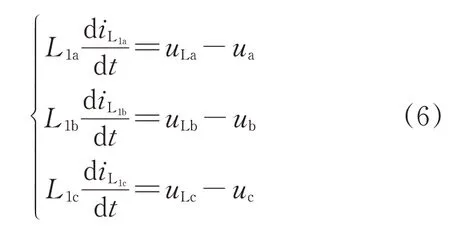
式中：L1a、L1b、L1c为LC 滤波器的三相电感；iL1a、iL1b、iL1c分别为流经L1a、L1b、L1c的三相电流；uLa、uLb、uLc分别为逆变器输出的三相电压；ua、ub、uc为电网的三相电压。

电容C的状态方程为：

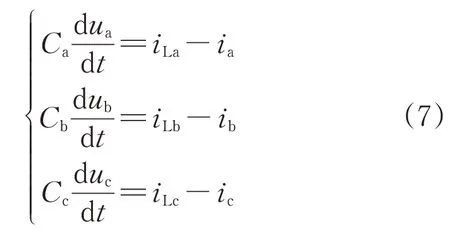
式中：Ca、Cb、Cc为LC滤波器的三相电容值；ia、ib、ic为光伏电源注入电网的三相电流。

将L1和C的状态方程进行派克变换得：

式中：iL1d和iL1q分别为iL1a、iL1b、iL1c派克变换到d、q轴的电流；uL1d和uL1q分别为uLa、uLb、uLc派克变换到d、q轴的电压；ud和uq分别为ua、ub、uc派克变换到d、q轴的电压；iLq和iLd分别为iL1a、iL1b、iL1c派克变换到d、q轴的电流。

式中：id和iq分别为ia、ib、ic派克变换到d、q轴的电流。

由于电容C的参数数值较小，因此，其注入的基波电流可以忽略，则：

将式（10）代入式（8）得：

由于iL1d和iL1q是一个常量，其微分值为0，故式（11）可以修正为：

结合式（5）和式（12）可得：

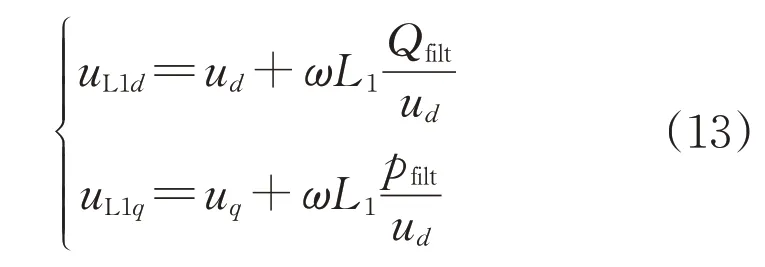
根据式（1）中调制信号幅值与基波电压幅值的线性关系，因此调制信号在派克变换后的公式为：

式中：Pmd和Pma分别为三相调制信号var、vbr、vcr派克变换后在dq坐标轴下的表达式，将其反派克变换得三相调制信号为：

式（15）为调制信号的幅值与光伏电源输出功率的函数关系，其中调制信号的幅值大小受光伏电源输出的有功功率、无功功率、并网处电压以及滤波器的电感参数的影响。

4 光伏电源的谐波源模型

通过机理分析得出调制信号幅值与功率的函数关系式，联立式（1）、式（15），将式（15）中基于恒功率控制策略获得的调制信号幅值M代入式（1）中调制信号的幅值Vrm，可得式（16），由式（15）可知调制信号幅值M的大小由pfilt、Qfilt、L1、ua、ub、uc计算可得。建立光伏电源并网的谐波电压源模型，以a相为例，光伏电源输出的a相谐波电压表达式为：

式中：Ush为逆变器输出的h次谐波电压；Pfilt和Qfilt为恒功率控制策略给定的基波有功功率和基波无功功率；Fh为函数关系式。

鉴于光伏电源经LC滤波器并网，则光伏电源注入电网的谐波电流的表达式如式（18）所示，图6为光伏电源并网的电路原理图。

图6 光伏电源并网简化原理图

式中：XL1h为LC 滤波器的h次谐波感抗；XCh为LC滤波器的h次谐波容抗；XL2h为系统的h次谐波感抗。

图7为光伏电源的谐波源模型的并网简化原理图，光伏电源的谐波源模型等效为一个受载波频率、并网处电压、发电功率、以及LC滤波器的阻抗参数、系统阻抗参数影响的受控电流源模型，Ish为谐波源发射模型发射的h次谐波电流，则其简化表达式为：

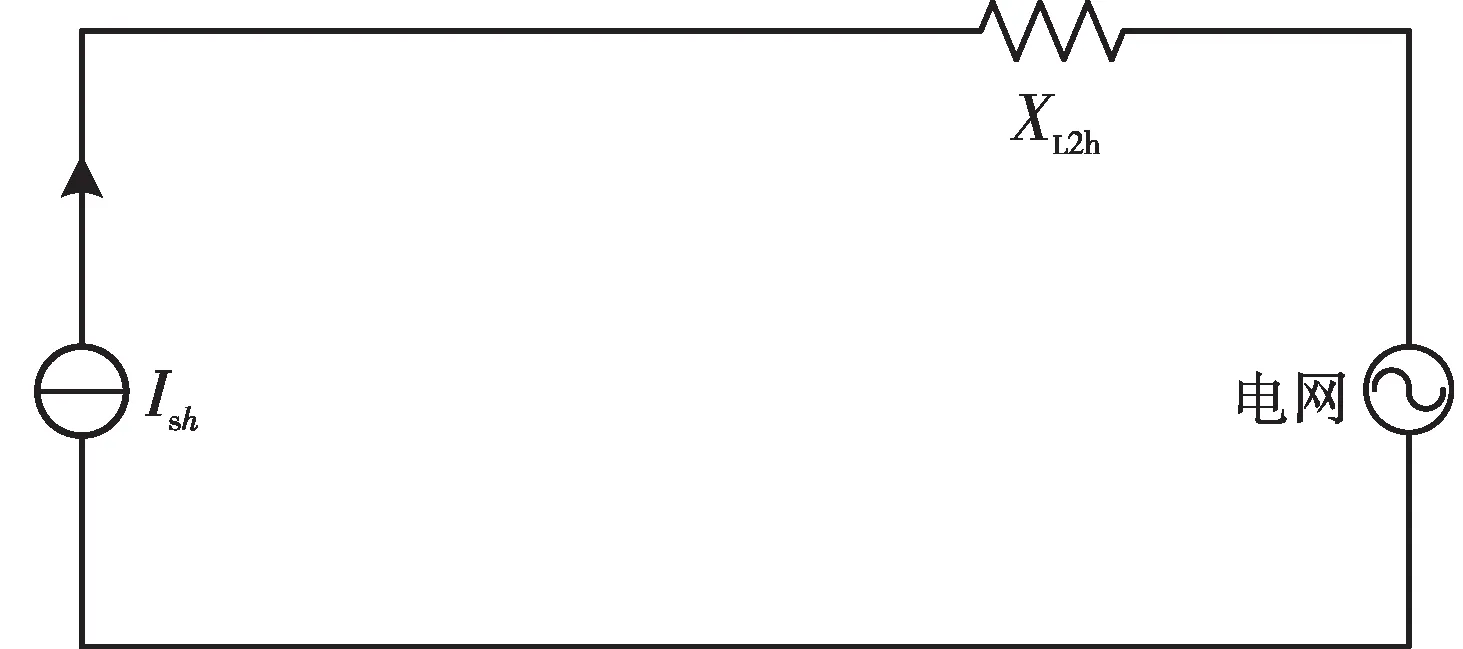
图7 光伏电源谐波源发射模型的并网简化原理图

5 仿真分析

为了验证搭建的光伏电源谐波源模型的准确性，采用PSCAD仿真软件搭建分布式光伏发电系统的并网仿真模型，如图8所示。其中，采用受控电压源模拟光伏电池的发电特性，逆变器和控制器被封装在DC-AC模块，外环控制器采用恒功率控制策略，Pref和Qref为给定的有功功率和无功功率信号。由于载波频率和LC滤波器的阻抗参数在光伏电源的实际运行是固定不变的，故仿真中将其设为固定值。光伏电源的额定有功功率为5 MW，额定无功功率为5 Mvar，载波信号的频率fc为500 Hz。仿真中测量公共连接点的电流和逆变器输出电压的瞬时值，将测量值进行FFT 分解，得到各次谐波电压和谐波电流的幅值，与式（16）计算得到的谐波电压的幅值和式（18）计算得到的谐波电流的幅值进行比较，从而验证建立的谐波源模型的准确性。

图8 分布式光伏系统并网的仿真原理图

为了衡量谐波源模型的准确度，采用平均相对误差SIF来衡量辨识谐波电流幅值的准确度，其表达式为：

式中：为采用式（18）计算的h次谐波电流幅值；为测量得到的h次谐波电流幅值；n为测量的总次数。

采用平均绝对误差SUF来衡量辨识谐波电压幅值的准确度，其表示式为：

式中：为采用公式（16）计算的h次谐波电压幅值；Uh为测量得到的h次谐波电压幅值；n为测量的总次数。

仿真实验中，SIF和SUF的参数越小，说明本文搭建的谐波源模型越准确。

受自然因素的影响，发电机组发出功率是不确定与波动的，导致给定的有功功率Pref和无功功率信号Qref是不确定的，故仿真实验随机输入分布式光伏发电系统的有功功率Pref信号和无功功率Qref信号，仿真中分布式光伏发电的额定有功功率为5 MW，额定无功功率为5 Mvar，载波信号的频率fc为500 Hz。

为了验证该谐波源模型可以较好地克服光伏电源功率的不确性与波动性，仿真中设置分布式光伏系统发出的有功和无功功率分别在额定值的0%～30%、0%～60%、0%～100%范围内随机波动，进行100次仿真实验。测量谐波电压和谐波电流的幅值，并与基于谐波源模型计算所得的值进行比较，表1为不同功率波动情况下误差值。在不同的功率波动情况下，SIF和SUF会随着功率波动范围的增大而增大，主要原因在于控制器是基于PI控制，存在一定的滞后性，且逆变器开关也存在一定的死区时间，当功率波动范围过大时，逆变器与控制器的滞后性会导致误差增大。但从仿真的数据看SIF和SUF依旧在误差允许的范围内，证明谐波源模型能较好地克服功率的波动性与不确性从而准确地计算光伏电源注入的谐波电流。

表1 不同功率波动情况下误差值%

由于8 次、10 次、12 次、19 次、21 次谐波电压和谐波电流的幅值比较显著，鉴于8 次与12 次的谐波电压的幅值接近，19次与21次的谐波电压的幅值也是接近相等的，仿真实验中，取额定值0%～60%波动的样本数据，将测量10次的谐波电压和谐波电流幅值与本文计算所得进行比较，绘制图9和图10。

图9 10次谐波电压测量值与计算值对比

从图9 和图10 中可以看出，在误差允许的范围内，理论计算和仿真测量的10 次谐波电压和谐波电流的幅值是十分接近的，在误差允许的范围内，可以认为该机理推导计算出的谐波源模型是合理的。

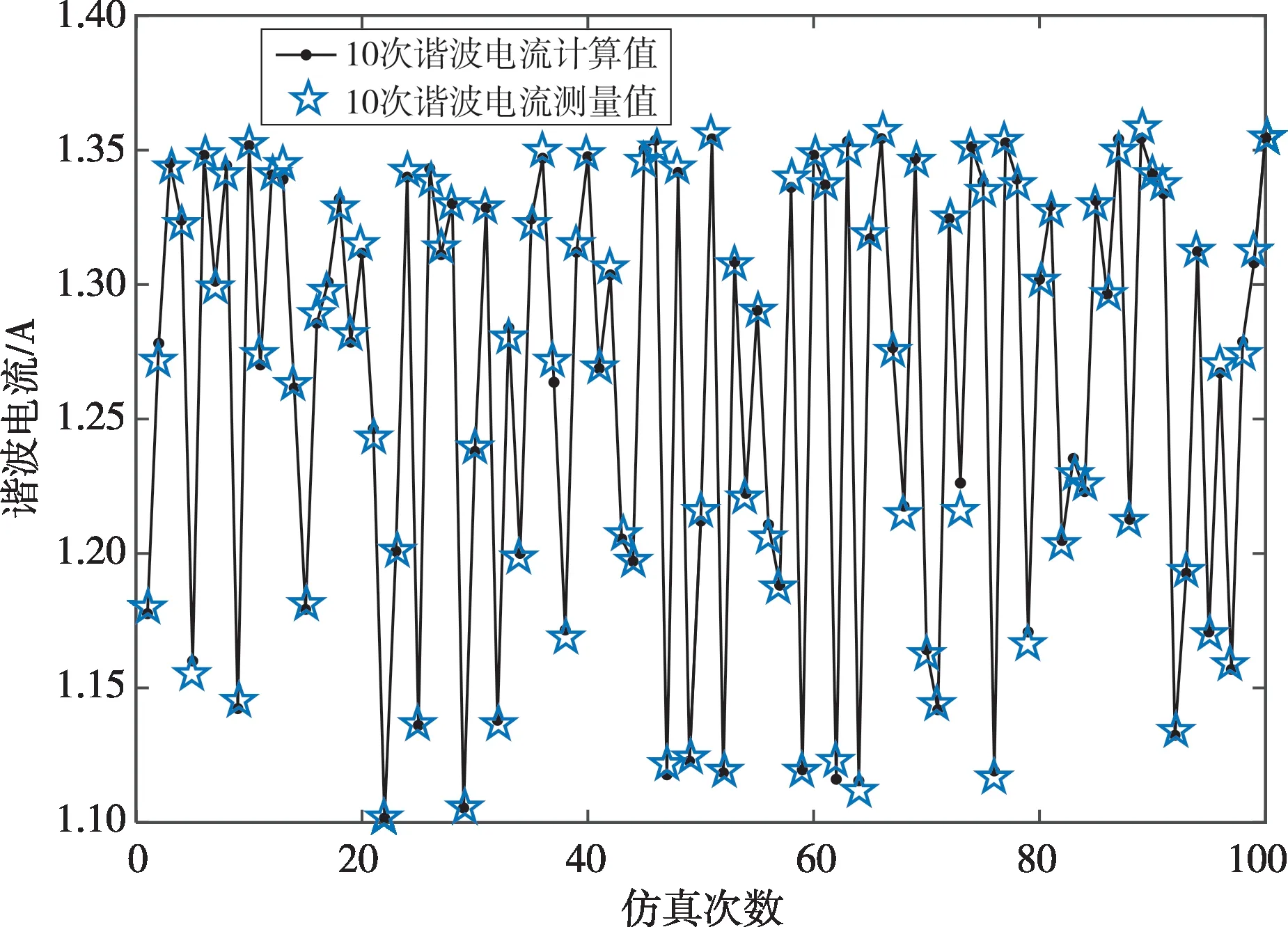
图10 10次谐波电流测量值与计算值对比

其中，任意取一组仿真情况，当分布式光伏发电发出的功功率为5 MW，无功为0 Mvar 时，图11和图12为其理论计算和仿真测量的各次谐波电压幅值和谐波电流幅值的柱状图。表2为谐波电压与电流对比值。在误差允许的范围内，理论计算和仿真测量的各次谐波电流和电压的幅值十分接近，证明了推导的谐波源发射特性的准确性以及建立的谐波源发射模型的合理性。

图11 光伏电源谐波电压计算值与仿真值的柱状图

图12 光伏电源谐波电流计算值与仿真值的柱状图

表2 谐波电压与电流对比值

6 结语

本文从机理建模的角度出发，建立了分布式光伏电源的谐波源模型，得出电源并网时注入电网的谐波电流受载波频率、并网处电压、发电功率、以及LC滤波器的阻抗参数、系统阻抗参数等因素的影响，并推导出该谐波电流的计算表达式。解决了目前分布式光伏电源谐波源模型欠缺的现状。由于模型能较好地表征光伏电源并网的谐波特性，为谐波责任分摊和谐波治理提供理论基础。