由电荷的量子性看静电场的能量计算

苑新喜

[中国地质大学(武汉)数学与物理学院 武汉 湖北 430074]

电荷的量子性是电荷最基本和最深刻的特征之一. 我们已经知道，电荷的基本量子单元就是一个电子或质子所带电荷量的绝对值，电荷的电荷量总是这个绝对值的整数倍.电子和质子不妨都可以称为基本单元电荷，简称基元电荷.

相对静止的电荷在周围空间产生的电场称为静电场. 静电场是电磁场的一种具体表现，同样具有能量、质量和动量等物质属性，电荷之间的库仑力就是经过静电场传递的.

自然，基元电荷自身固有一个静电场，该电场的能量称为基元电荷的电场固有能，也称为该电场的自能.作为基元电荷之一的电子，它的电场固有能及其对应(相对论意义上)的电磁质量至今仍然悬而未决[1].

在经典电磁场理论中带电体系的电荷由于数量巨大而通常被看成是宏观上连续分布的，从而忽略电荷微观上的量子性. 电荷的微观量子性与宏观连续性之间毕竟还是有本质区别的. 因此，应用经典电磁场理论计算宏观带电体的静电场能量时，最终计算结果只能局限于给出基元电荷之间一定体系范围内的相互作用能，根本上不包含基元电荷的固有能(自能).静电场能量计算上的这么一点局限性正是电荷微观量子性与宏观连续化之间本质区别的一种必然表现. 这点局限性让我们看到了静电场能量计算与场源特性之间所存在的一种内在关联性.

由于牛顿万有引力定律与静电场的库仑定律表达形式上的高度相似性，理论上很容易把静电场的能量密度公式推广到牛顿的万有引力场. 如果把静电场的能量计算与场源的特性之间那种关联性也同时推广到引力场，这样就可以帮助我们从一个特殊的角度认识和化解引力场的负能量问题.

1 静电场能量的计算

有关电磁学和电磁场的课程中都要涉及到一些静电场能量的计算问题[2～4]. 经典电磁场理论给出了几种不同的静电场能量计算的方法，这几种方法的计算结果彼此都可以相互呼应和验证. 其中，对静电场的能量密度进行积分是最基本和最重要的计算方法.经典电磁场理论给出真空中静电场E的能量密度

式中ε0为真空介电常数.宏观带电体的静电场总能量

由此可以求出一个半径为R、电荷量为Q的宏观均匀带电球面S的静电场总能量为

用此方法也可以求出一个半径为R、电荷量为Q的宏观均匀带电球V的静电场总能量为

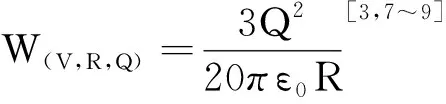
在这里，我们首先要说明的是，本文所涉及的计算都是一般电磁学和电磁场课程中的常见计算，故本文只给出计算结果，过程从略，下面也一样.其次，此处计算中带电球面S上和带电球V内电荷分布均看成是连续分布的. 最后，我们想强调的是，上面的计算结果无论W(S,R,Q)还是W(V,R,Q)肯定都不包含基元电荷的电场固有能(自能)，它们只能是组成电荷量Q的所有那些基元电荷之间一定程度或一定范围的相互作用能！也就是说用能量密度we计算静电场能量时存在一个无法突破的局限或界限.

电荷量Q所激发的静电场E从根本上说完全是由基元电荷的电场叠加构成的，但静电场E的能量却不包含基元电荷的电场固有能，这一点不能不让人觉得多少有些惊奇！造成这种情况的根本原因，就在于把电荷量Q看成是空间连续分布，这就完全忽略或屏蔽了电荷量子化的本质. 为了能更清楚地说明这个问题，下面我们再用另外一种常见的方法计算W(S,R,Q)和W(V,R,Q).

在经典电磁场理论中，也可以通过计算电势能的方法计算静电场的能量.首先，经典电磁场理论给出了由n个点电荷组成的宏观带电体系的相互作用能

式中φi为点电荷qi所在处除它之外的其他电荷所产生的电势，qiφi为qi的电势能. 这n个点电荷属于离散分布，每个点电荷单独存在时分别在空间激发各自的静电场. 不妨将点电荷qi激发的静电场记为Ei，Ei具有能量Wi，习惯上称Wi为点电荷qi的电场自能. 显然W(n,q)不包含这n个点电荷各自的电场自能Wi[6]，尽管体系的电场就是由这n个Ei叠加构成.W(n,q)只等于把这n个点电荷从当前位置移到彼此相距无穷远处时电场力所做的功.W(n,q)与点电荷各自的电场自能Wi没有任何关系，同时也就与基元电荷的电场固有能没有任何关系.

然后，将

直接推广到电荷连续分布的宏观带电体系. 不妨设宏观带电体系Q在空间的电势分布为φ，这时再将带电体系的电荷Q分割成一个个的电荷微元dQ，把W(n,q)中的累加符号相应地换成积分符号，得到公式

其中φdQ可以理解为dQ的电势能. 公式W(Q,φ)代表了计算宏观带电体系的电场能量的另外一个常见和重要方法. 由此，应用W(Q,φ)计算带电球面S和带电球V的静电场能量，同样得到与前面完全一致的计算结果W(S,R,Q)和W(V,R,Q)[2，8,9]. 既然前面的W(n,q)与基元电荷的电场固有能没有任何关联，W(S,R,Q)和W(V,R,Q)也一样与基元电荷的电场固有能没有任何关联！理论上W(S,R,Q)和W(V,R,Q)相当于这些基元电荷从当前位置移动到彼此相距无穷远时电场力所做的功.

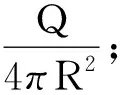
对于“宏观小，微观大”的点电荷而言，它实际上还是具有特定大小的物理尺度的，只要给出相应的物理尺度，它的静电场自能Wi就具有确定的数值. 比如当带电球面S和带电球V的半径R足够小，都可以看成是一个点电荷，但无论半径R多么小，只要给出R，其静电场自能都是一个确定的数值，但这个确定的计算结果依然只是基元电荷之间的相互作用能的总和，不包含基元电荷的各自的固有能. 电荷微元dQ在数学形式上可以趋于零(等同于“电荷可以无限细分下去”)，对应的dQ的静电场自能也可以趋于零，比如当电荷微元dQ均匀分布在球面S上时，其静电场自能也同步随dQ自身无限地趋于零. 显然，一个在数学形式上能无限地趋于零的电场自能与具有物理实在意义和大小的基元电荷的电场固有能没有任何关联.

对于微观带电体系如分子、原子，尽管单个的基元电荷也可以看成一个点电荷，但也不能计算出基元电荷的电场固有能. 并且在这些微观情形下，基元电荷的状态比较复杂，已超出经典电磁学的范畴，在此不展开讨论.

从微观粒子的内部结构上看，基元电荷的电场固有能是带电粒子质量的一个来源或组成部分，已融于物质的结构之中. 因此，不论带电体系的电磁场发生什么样的变化，基元电荷的静电场固有能(自能)都是一个保持不变的常数. 所以，在计算宏观带电体系的电磁场能量及其变化时，自然可以在形式上把基元电荷的电场自能排除在外[5].

最后，再举一个常见的计算电场能量的例子. 充电电容器存储的电场能量也是可以计算的，如板面为S、板间距为d的真空平行平板电容器存储的电场总能量

式中W(S,d,Q)也只表示电容器正极板上的电荷+Q与负极板上的电荷-Q在特定意义下的相互作用能，与基元电荷的电场固有能无关.

综上所述，静电场的能量计算与场源的特性之间存在着一种内在关联性.由于电荷的量子化本质，宏观带电体系静电场能量的计算与微观上基元电荷的电场固有能无关. 宏观带电体系的静电场能量本质上是基元电荷之间的相互作用能，在形式上可正可负；基元电荷的电场固有能作为物质结构的组成部分，只能是正的.

2 对引力场的负能量问题的一点启示

由于牛顿万有引力定律与静电场的库仑定律表达形式上的高度相似性，不可避免地引起了人们对引力场与电磁场的类比思考. 麦克斯韦不仅是经典电磁场理论的集大成者，也是引力场与电磁场类比研究的一位先行者. 1864年麦克斯韦把静电场的能量密度公式推广到引力场. 考虑到引力只有相互吸引作用，引力场的能量密度只能是负值，麦克斯韦认为这个“负能量”是不可接受的，并因此放弃了对引力的进一步研究.

在我们今天看来，电磁场是一种客观存在的特殊物质形态，具有物质实在性. 如果说，类比电磁场，传递引力作用的引力场也具有物质实在性，那么从这个角度看，引力场的“负能量”问题变得更加不可思议. 因此，引力场的负能量问题一直被看成是牛顿引力理论的一个逻辑“漏洞”或“缺陷”！

但是，如果我们在场源的特性上对引力场与电磁场进行类比，引力场的负能量问题未必不能解决. 电磁场的场源是电荷，具有量子性，那么我们是不是可以简单地设想一下引力场的场源(即引力质量)也具有和电荷一样的某些特性？假设引力质量也具有量子性，其量子化单元不妨称为“基元质量荷”， “基元质量荷”也有相应的引力场固有能(自能). 如果“基元质量荷”的引力场固有能存在，它应该是物质结构的组成部分，和基元电荷的电场自能一样.

今天我们所能探测到的引力场，都是名副其实的宏观引力体系所产生的.我们这里从3个层面将宏观引力体系与上述宏观带电体系进行类比.一是宏观引力体系的引力场可以认为是微观的“基元质量荷”的引力场的叠加构成；也就是说，宏观引力体系的引力质量分布在宏观形式上是连续的，在微观本质上是离散的.二是一旦把静电场的能量密度公式推广到引力场[11]，所计算出的宏观引力体系的引力场能量也一定都是“基元质量荷”之间的相互作用能.三是宏观引力体系的引力场能量也应该不包含“基元质量荷”的引力场固有能(自能)，也就是说，宏观上引力场能量(相互作用能)与微观上引力场固有能(自能)无关.因此不妨假设“基元质量荷”的引力场固有能(自能)恒为正，这个假设与宏观引力体系引力场的能量为负值的事实不产生矛盾，而且不影响宏观引力体系引力场能量的计算！这样我们把引力场能量问题分隔成宏观与微观两个不同层次上的问题，为在理论逻辑上化解了引力场负能量问题提供了一条可行的思路或途径.

基元电荷有正负，有电子或质子等不同的载体，因此可以说基元电荷的种类或载体不是唯一的. 那么，“基元质量荷”的种类或载体也可以类似地认为不是唯一的，电子与质子等不同的基本粒子是不是因此可以看成是不同种类或载体的“基元质量荷”呢？物质世界中基本粒子的种类毕竟是有限的，这是不是意味着引力场的场源事实上就是量子化的？其实这都是可以商榷的.

3 结论

由于宏观带电体系的电荷分布看成是连续的，完全屏蔽了电荷的量子性，所能计算出来的体系的静电场能量只是基元电荷之间一定程度或一定范围的相互作用能，不包含基元电荷的电场固有能，尽管宏观带电体系的静电场是由基元电荷的电场叠加构成. 类比电场，我们可以假设引力场的场源也是量子化的，这样就为解决引力场的负能量问题提供一个值得探讨的理论逻辑思路.