全尺寸海洋动态电缆关键物理特性试验与分析

2022-09-01郭毅,郭宏

电线电缆 2022年4期

郭毅, 郭宏

(1.上海国缆检测股份有限公司, 上海 200444; 2.中海石油(中国)有限公司北京研究中心, 北京 100028)

0 引言

随着我国海上油气田开发逐步走向深水和边际油气田,水下生产系统在我国的应用日益广泛,如陆丰22-1油田采用5口水下生产井口,采用水下增压泵回接到浮式生产储油轮(FPSO)上;流花11-1油田25口水下生产井口,使用“挑战号”半潜式平台进行生产控制并回接到“胜利号”FPSO;惠州32-5油田采用3口水下生产井口回接到已建的惠州26-1固定平台。水下生产系统作为深水海洋工程的一种重要开发模式,已经成为我国亟需研发的关键技术[1]。

典型的水下生产系统主要包括水下井口、水下采油树、水下管汇、水下处理设备、水下控制和监测系统、化学药剂注入系统、动态电缆/脐带缆、海底管线、立管、井口进入和维修系统设备等[1]。作为水下生产系统“神经生命线”的海洋动态电缆/脐带缆,长期由国外少数制造商供货,存在采购成本高、供货周期长、售后服务不及时等问题,在一定程度上制约了我国油气田的开发。

海洋动态电缆从设计、分析、生产、试验、安装与运行维护均需要对其关键物理特性有深入的了解。本工作结合数值建模与全尺寸试验,对深海油气开发中的典型动态电缆的物理特性进行了深入与全面的分析,为这类产品的国产化奠定理论基础。

1 数值分析

本工作中的海洋动态缆除了各项同性的内外护套外,各单元(如铠装钢丝、铜导体、填充等)均为螺旋缠绕非黏结结构。非黏结结构的特点是各单元在轴向对称载荷(如轴向张力作用下相互之间产生挤压),在非轴向对称载荷作用下(如弯曲载荷载荷作用下),相互之间产生相对滑移。从而导致了动态缆截面的物理特性不再像钢管一样是一个定值,而是跟载荷相关的非定值,其计算方法复杂,通常采用数值建模的方式进行计算。本工作使用UFLEX[2],该程序由挪威工业研究联盟海洋研究院(SINTEF OCEAN)开发。

1.1 物理模型与数值模型

本工作中的海洋动态缆实物截面对应的物理模型示意图见图1。

实物截面物理模型对应的数值模型见图2。

图2 海洋动态缆数值模型单元示意图

由图1、图2中可以看出:物理模型单元2,3,4,5,6被合并为数值模型中的铜导体护套单元;物理模型单元9,10被合并为数值模型中的内护套单元;物理模型单元12,13被合并为数值模型中的外护套单元;而物理模型中的光纤单元在数值模型中被忽略。在选择数值模型单元的材料时,采用了保守的处理方法,因而以上处理对于动态缆的物理特性的影响可以忽略不计。对上述物理模型单元采用合并处理后,大大减少了数值模型单元的数量,从而能够保证计算结果准确性的同时极大提高计算的效率。

动态缆在实际应用中,通常是采用两端挤压套环充填环氧树脂固定,因而截面作为一个整体承受各类载荷。UFLEX数值模型中可以通过设定截面的总体边界条件,使得截面作为一个整体加载各种载荷,包括轴对称载荷与不对称载荷,而截面内的各单元也根据各自的物理刚度分别承受相应的载荷。

1.2 单元物理特性

动态缆各单元的物理特性采用有限元程序UFLEX进行计算,数值模型中各结构的物理特性见表1,计算中采用的材料特性见表2。

表1 数值模型单元各结构的物理特性

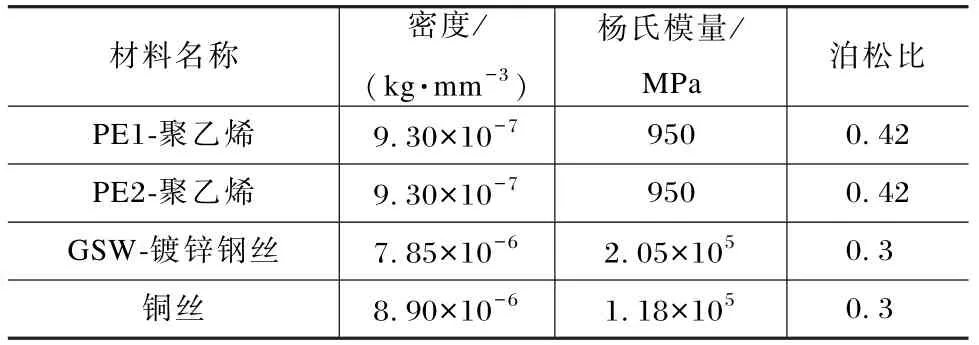
表2 材料特性

表1中的计算结果是各个单元单独计算的理想值。截面作为一个整体,其物理特性需要结合载荷与变形的关系得到。

1.3 截面物理特性

动态缆截面物理特性通常包括单位长度在空气中以及海水中的质量,截面的轴向刚度、扭转刚度、弯曲刚度以及截面的极限承载能力等[3-4]。

1.3.1 轴向刚度

截面的轴向刚度的计算可以通过截面在轴向张力下单位长度的变化率得到,即:

式中:EA为轴向刚度,MN;F为施加的轴向张力,N;Δl/l为单位长度的变化率,即应变。轴向张力与应变的关系图可通过有限元程序UFLEX得到,见图3。

图3 轴向张力与轴向应变关系图

图3中斜率即为轴向刚度。在UFLEX模型中加载时,施加轴向张力的同时,允许截面自由扭转。曲线拟合得到的轴向刚度为514 MN。

1.3.2 扭转刚度

截面扭转刚度的计算可以通过截面在扭矩作用下单位长度的转角变化得到,即:

式中:GJ为扭转刚度,kN·m2;Mx为施加的扭矩,kN·m;Δθ/l为单位长度的转角变化,即扭率,rad·m-1。扭矩与扭率的关系图可通过有限元程序UFLEX得到,见图4。其中图4(a)与图4(b)的区别在于施加的扭矩方向相反。

图4中斜率为扭转刚度。顺时针和逆时针曲线拟合得到的扭转刚度分别为211.0 kN·m2以及212.3 kN·m2,显示动态缆截面的扭转刚度在不同扭转方向并不完全一致。

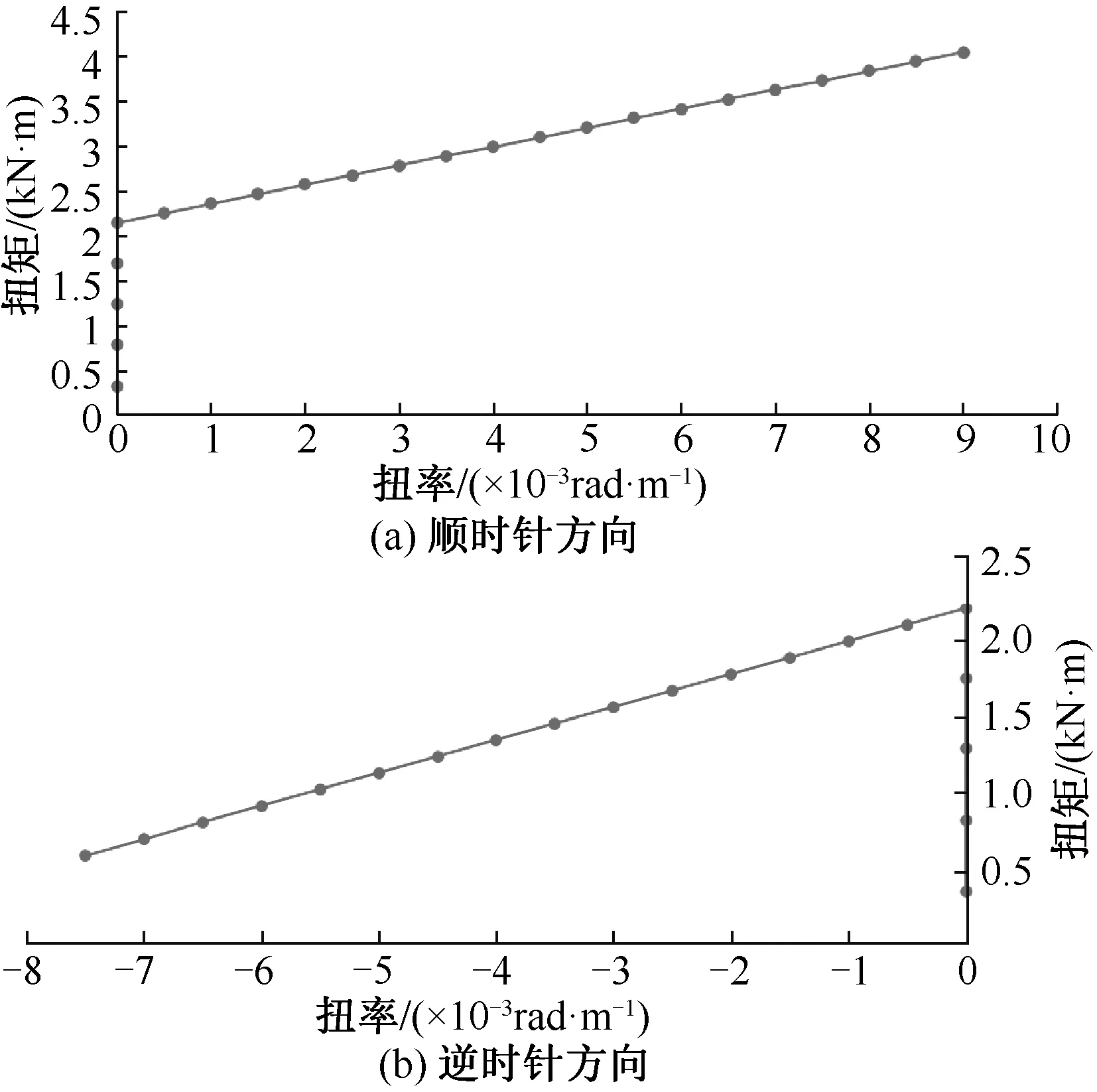
图4 扭矩与扭率关系图

1.2.3 弯曲刚度

截面的弯曲刚度的计算可以通过截面在弯矩作用下曲率的变化得到,即:

式中:EI为弯曲刚度,kN·m2;My为施加的扭矩,kN·m;κ为曲率,m-1。弯矩与曲率的关系图可通过有限元程序UFLEX得到,见图5。

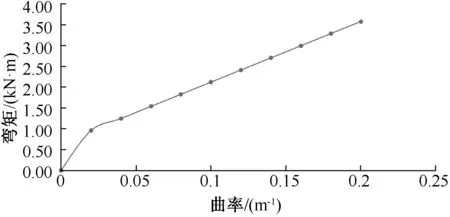
图5 弯矩与曲率关系图

由图5可知,弯矩与曲率的关系不再表现为简单的线性关系,而是呈现出明显的双线性关系。曲线的斜率,即截面的弯曲刚度有一个突变的过程,在突变点以前,截面的刚度值明显大于突变后的截面刚度值。刚度的突变点被称为非黏结螺旋结构单元的临界滑移曲率。

动态缆截面在轴向张力作用下,非黏结螺旋结构单元会产生向截面中心的位移,由于受到比螺旋单元结构更靠近截面中心的其他单元的限制,或者螺旋结构单元之间的限制,该位移被限制,从而在结构单元之间引发接触,接触压力的大小与螺旋单元的缠绕角度以及施加的轴向载荷有关。在保持轴向张力的同时,再施加非轴向对称载荷,此处为曲率及弯曲载荷,由于载荷沿截面径向的非对称性,导致螺旋结构单元内产生剪切力,如果螺旋结构单元处于不受限制的自然状态,该剪切力将导致螺旋结构沿着螺旋结构单元的螺旋缠绕方向产生运动。但事实上,该螺旋单元跟周围其他单元处于接触状态,由于材料之间存在摩擦,会在接触面上产生摩擦力,从而限制螺旋结构单元与其他结构单元的相对运动。

当弯曲载荷较小时,弯曲导致的剪切力与螺旋结构单元受到的摩擦力平衡,此时螺旋结构单元与其他单元之间不发生相对运动,尽管动态缆截面的单元之间是非黏结的,整个截面的力学特性跟刚性管类似,截面的弯曲刚度大,此时截面处于非滑移状态。黏结状态下的弯曲刚度可由动态缆截面内的所有单元的弯曲刚度叠加得到。随着弯曲载荷的增加,螺旋结构单元内的摩擦力不足以平衡单元内的剪切力时,螺旋单元发生相对运动,曲率增加的速度加快,截面的弯曲刚度降低,此时截面处于滑移状态。滑移状态下的弯曲刚度主要由动态缆截面内的同心圆结构层的弯曲刚度叠加得到,如外护套层和内护套层。

本工作中动态缆的滑移弯曲刚度为14.54 kN·m2。滑移弯曲刚度在动态缆的产品标识中被标为名义弯曲刚度,在工程设计的前期使用。名义弯曲刚度对动态缆在海洋环境中的总体响应分析影响较大,尤其是对动态缆的疲劳特性影响显著,在采用名义弯曲刚度不能满足工程设计要求时,通常采用图5所示的动态缆截面真实的弯矩与曲率关系,替代名义刚度进行总体响应分析。需要说明的是,弯矩、曲率关系与轴向张力相关联,因而总体响应分析模型中使用的弯矩、曲率关系是与截面内的张力水平有关的一个函数,该函数通过在截面分析中改变轴向张力水平得到。

2 全尺寸试验

非黏结动态缆通常截面单元构成复杂,上述采用的数值建模方法中通常会采用各种假设,比如螺旋结构单元的滑移路线假设,得到的物理特性在很多情况下并不能精确反映实际产品的情形;同时动态缆在生产的过程中,由于生产工艺导致的内力在数值模型中也难以得到精确描述,因而通常需要进行试验验证[5]。

海洋动态缆通常需要进行全尺寸的物理特性验证试验与疲劳试验。其中,物理特性的验证试验是进行疲劳试验工况设计的基础,因而有必要单独进行阐述。本工作对一种应用广泛的典型海洋动态缆进行了全尺寸的物理特性验证试验,而疲劳试验由于涉及动态缆的动力响应分析以及海洋动态载荷与试验载荷的转换,本工作暂不讨论。

2.1 试验装置

典型的全尺寸试验装置示意图见图6,其中图6(a)为试验装置的整体示意图,图6(b)为防弯器与端头连接处的放大示意图。

图6 动态缆全尺寸拉弯组合试验装置

图6(a)中左端为摆动塔,模拟动态缆跟海面浮体的连接部分,右端为轴向张力液压加载端,模拟动态缆悬挂在浮体上由于自重产生的轴向张力。试验装置中涉及了两个旋转点,以确保试验样品在轴向张力与弯曲的联合作用下其力学行为与实际悬挂在海面浮体时一致。

全尺寸试验装置需要满足美国石油协会API 17B对此类试验装置与试验样品的要求:

(1)试验样品两端需要与实际使用时一致的端头,以及需要装备防弯器。

(2)试验样品弯曲加载端的端头与防弯器固定法兰间的距离不小于动态缆外层铠装钢丝的1倍螺旋截距,除非端头与防弯器直接通过法兰连接。

(3)试验样品轴向张力加载端的端头与防弯器尾端的距离不小于动态缆外层铠装钢丝的3倍螺旋截距。

2.2 试验装置模拟

动态缆的全尺寸试验需要模拟动态缆在真实海洋环境下受到的环境载荷,即张力与弯曲载荷。在试验中,张力通过图6中右端的液压加载器实现。弯曲载荷通过液压驱动的摆动塔实现,试验中使用了两套液压加载系统,加载时采用位移控制,确保施加到试验样品上的曲率与实际总体分析得到的曲率一致。本工作采用了SINTEF OCEAN开发的SIMLA有限元软件对试验装置进行了模拟。有限元模型中,下列结构作为刚性结构处理:①试验夹具;②摆动塔;③端头;④张力液压加载器;⑤防弯器钢结构插入段。模拟情况见图7。

图7中(a)图为试验装置的有限元模型不加载荷时的情形,(b)图与(c)图为摆动塔处于最大15.0°与最小-15.0°摆动角度时的情形。

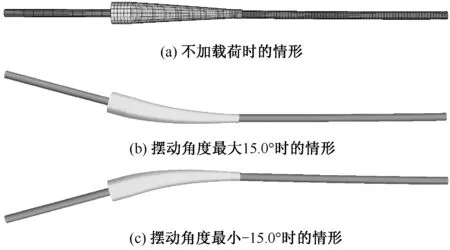
图7 动态缆全尺寸拉弯组合试验样品SIMLA模型

摆动塔处于不同位置时曲率沿着试验样品纵向的分布图见图8。图8中,曲线1~13所对应摆动塔的摆动角度依次为15.0°,12.0°,9.0°,6.0°,3.0°,1.5°,0°,-1.5°,-3.0°,-6.0°,-9.0°,-12.0°,-15.0°。

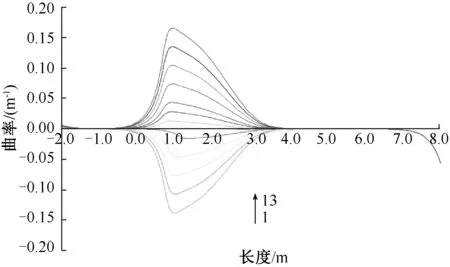
图8 试验样品曲率分布图

由图7中可以看出,摆动塔处于不同摆动角度时最大曲率点均处于防弯器内部,从而说明试验中采用的防弯器实现了将最大曲率限制在防弯器内部的目的;由图8中可以看出,最大曲率发生的位置随着摆动角度的大小变化基本保持不变。

2.3 结果与讨论

本工作重点讨论动态缆在轴对称载荷下的响应。试验步骤如下:

(1)周期1:轴向张力增加到125 kN,然后匀速将该张力增加至175 kN,保持张力水平在175 kN,最后从175 kN匀速减少至125 kN,记为125 kN—175 kN—175 kN—125 kN;

(2)周期2:重复125 kN—175 kN—175 kN—125 kN;

(3)周期3:重复125 kN—175 kN—175 kN—125 kN;

试验样品的轴向张力与加载端转角加载图谱见图9。

图9 试验样品中轴向张力与加载端转角加载图谱

由于试验样品的截面设计在扭转方向上的不平衡,当截面在轴向张力的作用下截面发生耦合扭转,从而导致截面加载端转角产生一定角度的转动。

本工作第二部分讨论扭转刚度时已经看到动态缆的扭转刚度在不同扭转载荷作用略微有些差异,显示了截面的扭转不平衡。从而在轴向张力作用下,动态缆的截面将发生一定角度的旋转。

试验样品张力加载端的位移与轴向张力的关系见图10,两者的关系反映了试验样品的轴向刚度,如公式(1)所示。

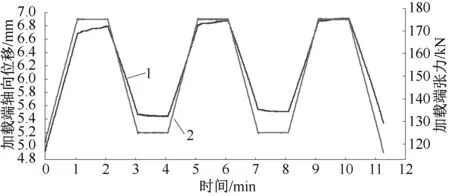
图10 试验样品中加载端位移与轴向张力关系图

根据图9与图10,可以得到试验样品中轴向张力与轴向位移的关系,见图11。图11中显示了轴向张力从125 kN—175 kN—125 kN—175 kN—125 kN—175 kN—125 kN变化时,试验样品张力加载端的位移变化情况。

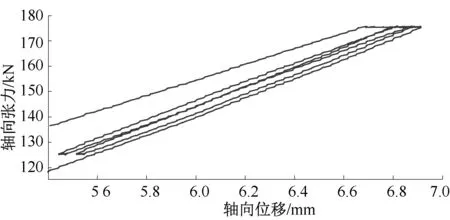
图11 试验样品中轴向张力与轴向位移的关系

由图11可以看出,加载阶段的曲线与卸载阶段的曲线不重合,张力保持期间试验样品依然有位移产生;图11中还显示出,不同加载周期时加载曲线与卸载曲线的距离随着加载周期的增加而减少。

动态缆加载阶段和卸载阶段的轴向刚度可以通过计算轴向张力增加与减少阶段的斜率得到,结果见表3。

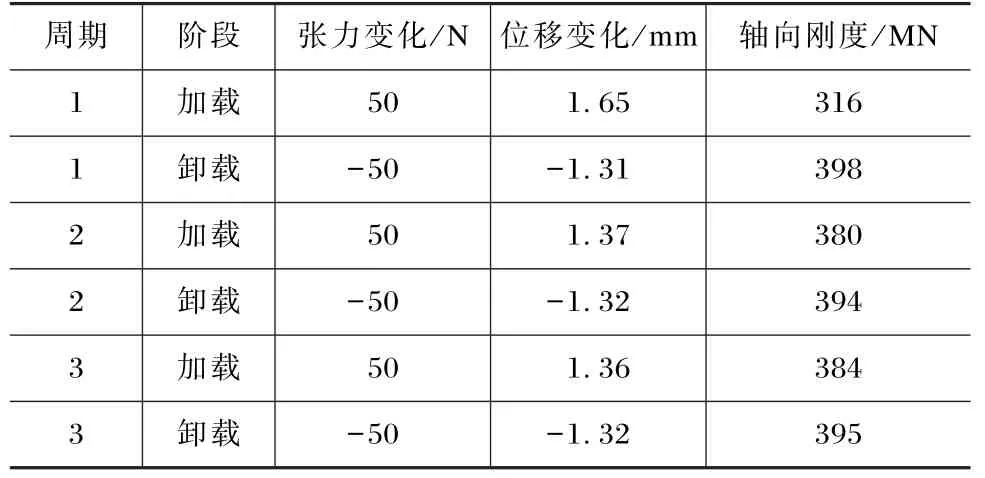
表3 试验样品轴向刚度试验值

由表3中试验数据可知,动态缆的轴向刚度在380~400 MN之间,在加载阶段与卸载阶段的轴向刚度略有不同,第一个加载阶段的轴向刚度明显低于后面两个加载阶段的测量值,3个卸载阶段的轴向刚度值吻合良好。试验数据还显示动态缆轴向刚度随着加载周期的增加而略有增加,预计随着加载周期的增加,试验值将趋向于收敛(加载曲线与卸载曲线趋向重合)。

图3中数值分析得到的轴向刚度为514 MN,相比试验得到的刚度约超过25%。造成这一差异的原因之一是数值模型中,在轴向张力作用下,轴向位移小于实际结构在轴向张力下的轴向位移。试验样品因成缆工序导致截面内单元之间结合紧密度降低,从而导致在同样张力下的位移增加;另一个原因是数值模型中,螺旋结构单元之间的接触刚度的取值基于经验估计而不是实际测量值,即使采用测量值,单元之间的具体接触情况(如接触面积)也会受到成缆工艺的影响,从而影响轴向刚度的试验数值。