高速列车运行场景监测数据融合算法研究
2022-09-01胥如迅马军惠孟建军李德仓陈晓强
胥如迅,马军惠,孟建军,2,3,李德仓,2,3,陈晓强
(1.兰州交通大学机电技术研究所,兰州 730070;2.甘肃省物流及运输装备信息化工程技术研究中心,兰州 730070;3.甘肃省物流与运输装备行业技术中心,兰州 730070;4.兰州交通大学机电工程学院,兰州 730070)
近年来随着我国铁路建设网愈加庞大,列车运行环境也愈加复杂,列车设施设备的复杂性、人的不可预测性以及环境的不确定性,有时会引发严重的铁路交通事故[1].例如,2007年2月,开往阿克苏的5806次列车途径新疆戈壁大风地区时遭遇强风袭击造成11节车厢倾覆、34名旅客死亡的严重事故;2020年3月途径郴州市永兴县的T179次列车与入侵线路的滑塌体相撞,造成严重的人员伤亡事故;2021年5月,因大风吹扬地膜致接触网故障造成部分高铁晚点,导致成千上万旅客滞留北京西站;由此可见,监测铁路沿线环境保证列车运行安全至关重要.铁路运行环境易受自然环境与人为失误因素的威胁,自然因素方面,强风致使列车脱轨、雨天致使行车轨道湿滑、大雾干扰行车视线以及山体滑坡入侵线路等;人为失误因素方面,塑料薄膜等异物入侵铁路限界、铁路沿线违章作业以及禁牧区违规放牧等[2].
多传感器数据融合技术作为一种重要的数据处理手段,在医疗诊断、遥感测绘、环境监测等方面有着广泛的应用[3],尤其在长距离带状区域如铁路沿线、煤矿内部巷道、高速公路沿线以及电网监测等[4]方面具有显著优势.我国高速列车运行环境复杂多变,通过部署多传感器得到的监测数据,其可靠性和准确度比单一传感器更能达到要求,数据融合技术既能够适应环境的动态变化又能降低干扰因素对系统的影响[5].因此,研究适用于高速列车运行场景监测的数据融合算法可为后续铁路数据融合平台架构提供重要参考.
1 多传感器数据融合技术
数据融合技术是运用单模型算法或多种模型组合算法,对多传感器采集信息进行融合分析处理,使得决策结果的准确度和可靠度更有利于对实际情况的判断[6].加权算法是众多学者研究的算法之一,所谓加权是对测量数据分配以合理的权重,其难点是如何分配最优权重以达到最佳的融合结果.文献[7]在数据传输前,利用Grubbs准则排除测量数据中的过失误差,自适应加权算法融合之前用算术平均和批量估计进行数据预处理,提高了融合精度;文献[8]在分批估计的基础上引入修正因子来调节自适应加权因子,提高了融合精度;文献[9]为克服提前给定的权重因子不适应环境的变化致使决策结果错误,综合考虑数据的一致性、当前权重以及综合影响因子,使融合结果更加准确;文献[10]提出了一种ADAEWF算法,提高了融合精度,但该算法只有监测到足够多的异常数据才能触发运行;文献[11]采用分布图法找到并淘汰异常数据,采用自适应加权融合算法,并通过关系矩阵寻找支持度最高的测量数据代替淘汰的异常数据,该算法提高了数据的完整性.文献[12]为克服传统的自适应加权融合算法中测量值选取的弊端,用数值迭代的思想改进对测量值的选取.
综上所述,在采用数据融合算法之前需要进行一致性判断,通过定义距离函数求取一致性矩阵,同时求取各传感器的综合支持度,从而判定是否存在异常数据并选择最佳数据集参与融合过程.一方面,阈值的选取依赖大量的数据处理经验且过于绝对化,导致数据融合结果受主观因素影响较大,对实际情况易造成误判;另一方面,异常数据的剔除减少了精度较低的传感器参与数据融合的可能性,这有违采用多传感器数据融合的初衷.
本文提出的数据融合算法基于文献[13]提出的在线迭代与局部融合思想,以一种新的置信距离和自适应加权估计算法为理论基础,一方面扩大参与数据融合的传感器数量,增加精度较低的传感器参与数据融合的可能性,从而提高数据融合精度;另一方面采用自适应加权融和估计算法,自适应的为各个传感器分配最优加权因子,从而提高融合结果的可靠性,可应用于测量数据庞大的铁路运行环境数据级融合过程.
2 算法模型及原理
2.1 自适应加权融合算法
自适应加权融合算法的核心思想是:基于总均方误差最小的前提,利用各传感器采集数据及测量精度,自适应的为各传感器分配最优加权因子[14],加权因子分配的越精确,数据融合结果则越贴近真实值,图1为自适应加权融和估计模型.
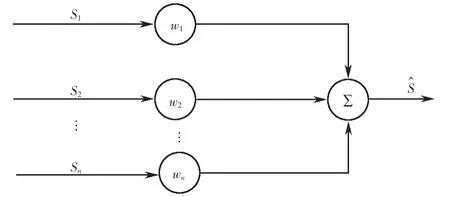
图1 自适应加权融和估计模型Fig.1 Adaptive weighted fusion and estimation model

2.2 关系矩阵



3 算法仿真
3.1 算法处理流程
本文算法是根据新的置信距离测度将关系矩阵变换成对称矩阵,依据关系矩阵寻找支持度最大的传感器组,若通过判定处理将传感器组的测量数据采用自适应加权算法融合处理,融合结果记为复合传感器的测量数据,并与剩余传感器的测量数据建立关系矩阵,重复上述步骤,直至不再具有通过判定处理的数据为止;在线迭代过程中发现某些局部融合结果与其它传感器的测量数据间具有潜在一致性,可以更充分地发掘多传感器测量数据的效用,有效地改善多传感器判定数据一致性后直接剔除异常数据的弊端.具体的算法处理流程如图2所示.
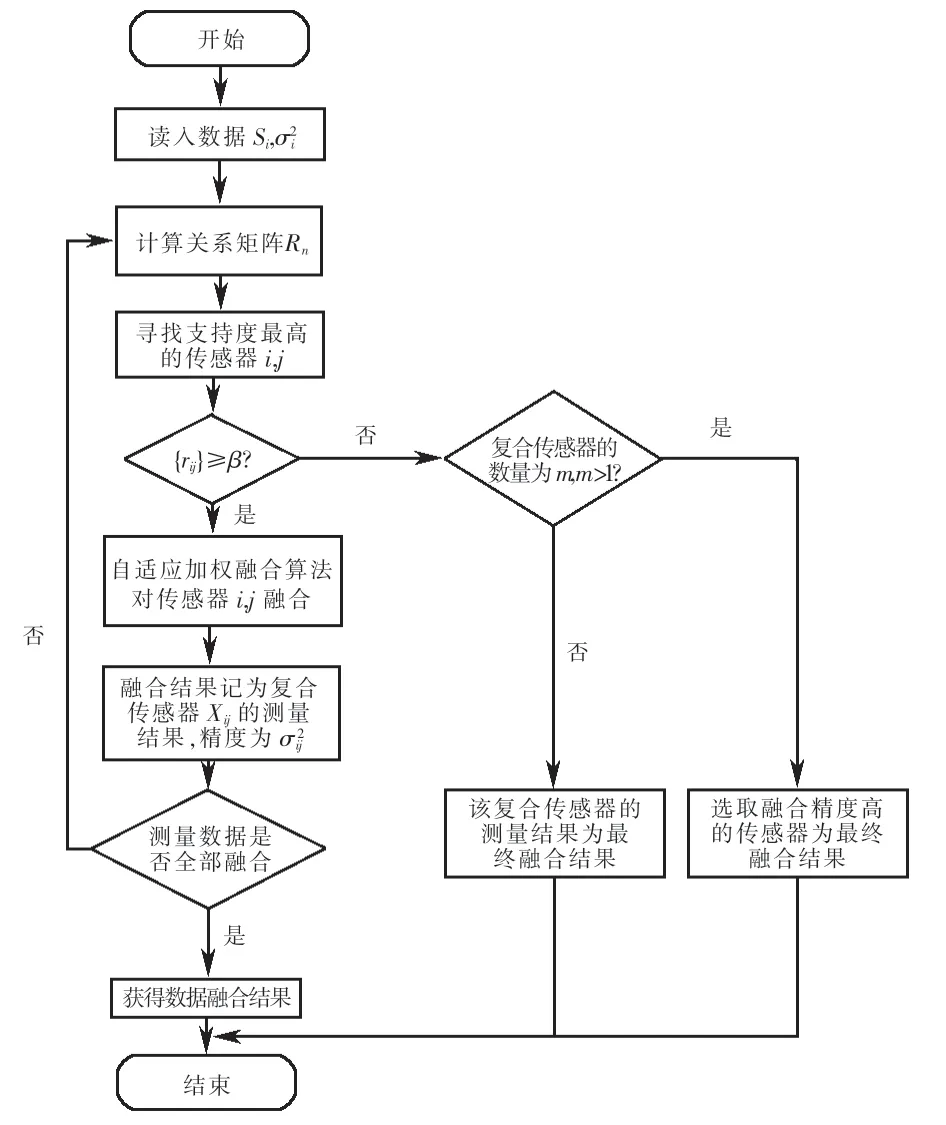
图2 算法处理流程Fig.2 Algorithm processing flow chart
3.2 算法仿真
本文使用Matlab进行仿真,表1为6个传感器在7个采样时刻测量的同一特性参数,特性参数的实际值为50.表2为各传感器的测量精度.
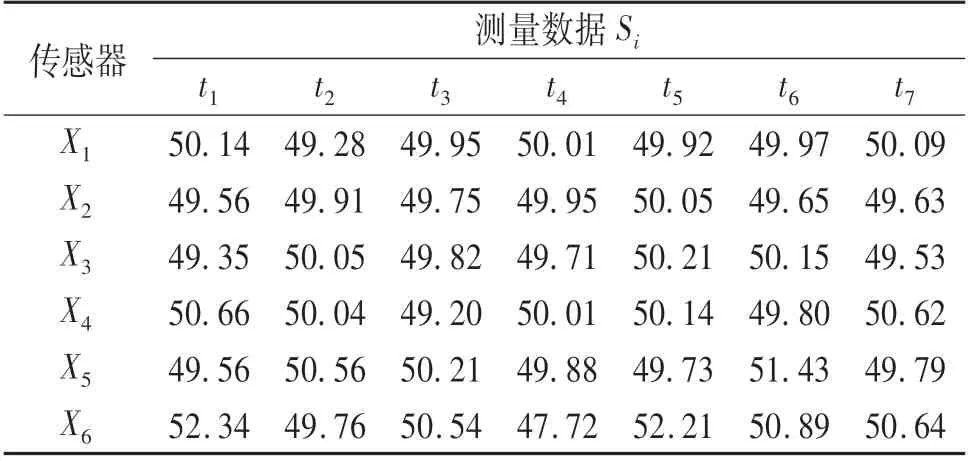
表1 传感器采集数据Tab.1 Data collected by sensors

表2 传感器测量精度Tab.2 Sensor measurement accuracy
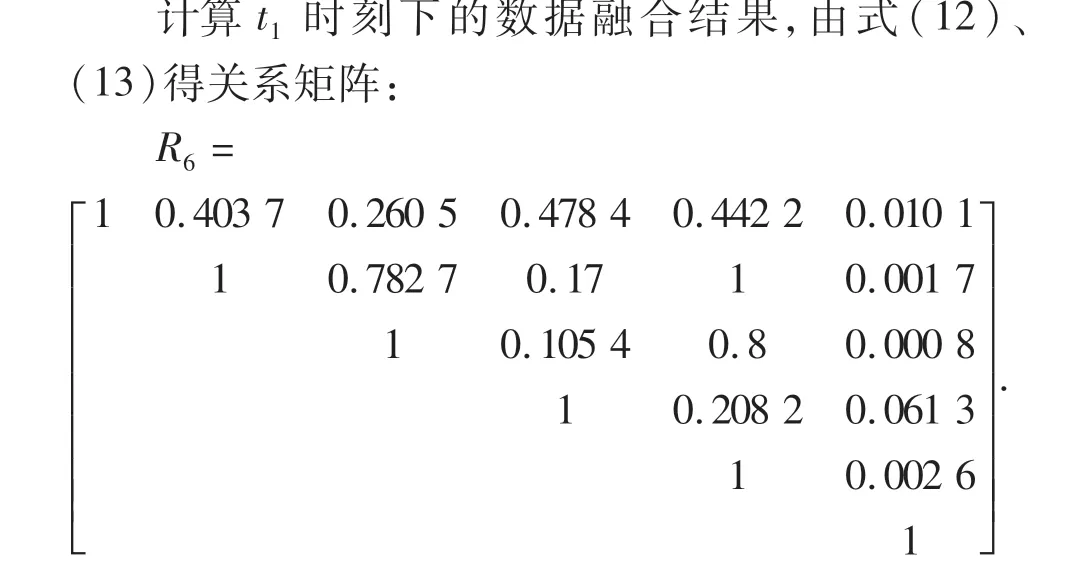
可见,r25=1为上三角矩阵中最大值且大于门限值0.01(此例中上限值取0.01),表明传感器X2和传感器X5的支持度最大,对这组传感器采用自适应加权方法融合,得到:
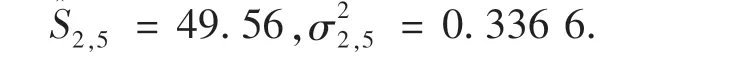
将上式计算结果看作是复合传感器X(2,5)的一次测量数据,此时变成了一个5传感器组,表3为5传感器组的测量数据及其精度.将上式结果看作是复合传感器X(2,3,5)的一次测量结果,此时还剩4传感器组,限于篇幅,这里不再赘述关系矩阵的计算结果,仅列出每次得到的上三角矩阵中支持度最大值以及自适应加权融合结果.
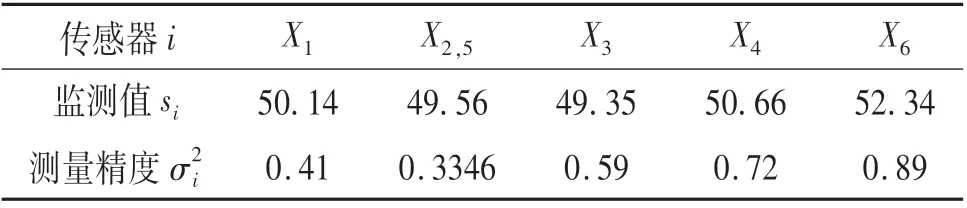
表3 5传感器组采集数据及精度表Tab.3 Data collection and precision table of 5 sensor group

1)进行局部融合后剩余为4传感器组,计算关系矩阵,得出传感器X1和传感器X4支持度(r14=0.478 4)最大且大于门限值0.01,因此将传感器X1和传感器X4的监测数据采用自适应加权进行局部融合得到:
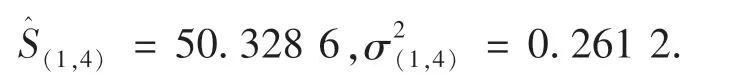
2)进行局部融合后剩余为3传感器组,计算关系矩阵,得出复合传感器X(1,4)和复合传感器X(2,3,5)支持度(r=0.082 9)最大且大于门限值0.01,因此将传感器X(1,4)和传感器X(2,3,5)的测量数据采用自适应加权进行局部融合得到:
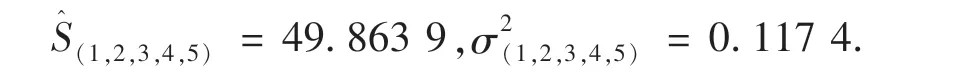
3)进行局部融合后剩余为2传感器组,计算关系矩阵矩阵,得出复合传感器X(1,2,3,4,5)和传感器X6支持度(r=0.004 3)最大但小于门限值0.01,因此不再进行融合,通过比较剩余的2个传感器组,选取融合精度最高的一个,即复合传感器X(1,2,3,4,5),最终融合结果为:

为验证本文算法的有效性,将数据融合结果与算数平均值法(算法1)、传统自适应加权估计算法(算法2)所得结果进行对比,如表4所示.由表4可以看出本文所提算法极大的提高了估计的参数精度且误差更小,具有较高的可靠度和准确性.图3是表4中对应的算法仿真结果对比图,本文算法在融合结果上更趋于实际值,且更收敛,而使用算法1和算法2得出的融合结果将大打折扣.

表4 各融合算法数据融合结果对比Tab.4 Comparison of data fusion results of each fusion algorithms
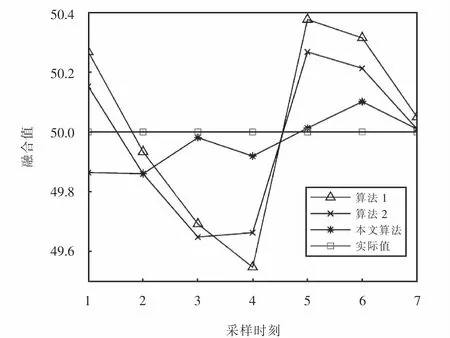
图3 各融合算法数据融合结果对比Fig.3 Comparison of data fusion results of each fusion algorithms
图4为不同融合算法在各采样时刻下的绝对误差与相对误差变化过程,从绝对误差变化过程来看:使用算法1仿真后的融合结果与实际相差较大,且绝对误差变化剧烈;使用算法2对数据进行处理后,系统的绝对误差显著降低,但仍然存在较大误差且变化幅度有所缓和;使用本文算法绝对误差低于前两种算法且变化平缓呈收敛趋势.在时刻精度最低的传感器测量数据误差大,使用算法1和算法2得到的融合结果绝对误差过大,而使用本文算法可以在迭代的过程中有效的避免该数据参与数据融合,在、时刻,传感器的其测量数据误差小,在迭代过程中参与了数据融合,有效的证明了本文算法抗干扰能力强,增加了精度较低的传感器参与数据融合的可能性,因此,本文提出的数据融合算法估计的参数精度明显提高且误差小.
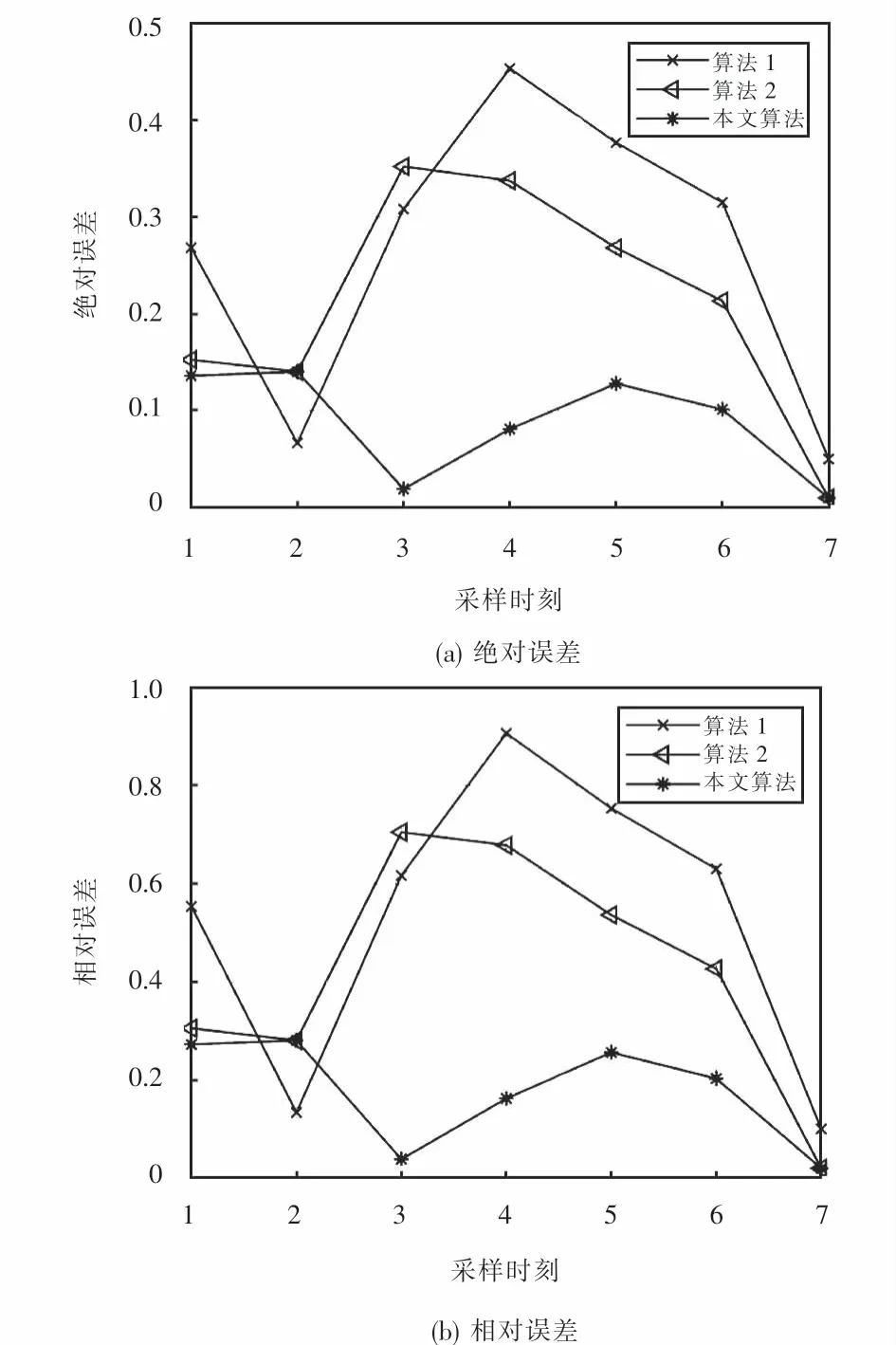
图4 各融合算法的误差对比Fig.4 Error comparison of each fusion algorithm
4 结束语
本文探讨了高速列车运行场景监测数据融合问题,针对现有数据融合方法的缺点,运用在线迭代与局部融合的思想,将支持度高的传感器组进行局部融合,其结果记为复合传感器测量数据,以发现更多的潜在数据一致性,既避免异常数据参与融合处理,又提高了融合结果的准确性和可靠度,可应用于测量数据庞大的铁路运行环境数据级融合过程.需要指出的是虽然本文提出的方法需要付出一定的计算代价,每次局部融合后产生的新的复合传感器要与其他传感器进行一致性判定,增加了一定的计算量,但是由于计算机水平的发展,这是可以克服的.
