兰新高铁桥梁挡风屏对正馈线气动特性的影响
2022-09-01何亚萍张友鹏赵珊鹏王思华
何亚萍,张友鹏,赵珊鹏*,2,王思华
(1.兰州交通大学 自动化与电气工程学院,兰州 730070;2.兰州交通大学 甘肃省轨道交通电气自动化工程实验室,兰州 730070)
兰新高铁位于甘肃、青海和新疆境内,东起兰州,途径西宁,西至乌鲁木齐,线路全长1 776 km,其中大风区线路长579.6 km,占线路总长的32.6%.沿线地形地貌复杂,经过荒漠、戈壁和山谷等特殊地形,常年遭受风灾侵扰.兰新高铁沿线风区主要有甘肃境内安西风区和新疆境内百里风区、烟墩风区、三十里风区及达坂城风区[1-2].大风区段内风速高、风期长、起风速度快且季节性强,大风引起的风沙流易导致轨道积沙、钢轨磨损增大,迫使列车停运,旅客被滞留,严重时可导致列车脱轨或倾覆等事故频发[3-4].
为保证列车安全稳定运行,兰新高铁大风区段沿线设置了挡风墙(屏).“防车不防网”设置的挡风墙(屏)虽然能够有效阻止轨道积沙与列车倾覆,但是也导致了大风沿挡风墙向上爬升,对挡风墙(屏)后方区域风速产生了增速效应,而接触网正馈线正好位于此增速区域内,因此致使正馈线发生舞动现象[5],如图1所示.大风引起的舞动造成线索、金具磨损严重,正馈线与保护线线间距离不足,引起放电跳闸事故,对列车安全稳定运行造成一定的干扰,因此有必要进一步明确兰新高铁正馈线舞动的激发因素.

图1 兰新高铁正馈线舞动现场图Fig.1 Galloping site diagram of positive feeder of Lanzhou-Urumqi high-speed railway
针对桥梁结构下的挡风屏气动特性问题,相关学者已做了一定程度的探索.文献[6]针对日本铁路沿线强风引起的列车车辆事故,研究分析了作用在列车车辆上的空气动力和强风特征;文献[7]通过全尺寸、风洞试验及计算流体力学方法得到了横风空气动力和力矩系数等信息,然后给出了测量和计算得出的车辆周围流场图,并描述了稳态和非稳态气动力特性;文献[8]通过风洞试验测试了桥梁上方的流场分布,并分析了高架桥上挡风屏的遮蔽效率;文献[9-10]研究了高架桥上声屏障高度变化对高速列车头车、中车及尾车侧风运行气动特性的影响,研究仅限于对列车的气动特性分析,未能对接触网正馈线进行分析研究;文献[11]以百里风区桥梁挡风屏为研究对象考虑挡风墙、防风明洞等相邻挡风设施及风向角、线路布局等影响因素对挡风屏遮蔽效应的影响;文献[1]根据挡风板对列车气动特性的影响规律,设计了一种适用于桥梁挡风结构的挡风板,并确定了挡风板波高和板厚等技术参数;文献[12]通过风洞数值模拟研究分析了挡风屏设置形式对列车侧力系数与倾覆力矩系数的影响规律;文献[13-14]针对兰新高铁路堤结构下挡风墙对正馈线产生的影响进行了研究,包括挡风墙高度、宽度及正馈线位置等因素,但未考虑桥梁结构下挡风屏对正馈线产生的影响;文献[15]在桥梁结构上选用透风率为30%的挡风屏,对比分析了无挡风屏、单侧挡风屏及双侧挡风屏的高度与接触线处风速间的关系.分析当前研究现状可知:针对大风区桥梁挡风屏的研究大多为分析挡风屏对列车气动特性以及对接触线的影响,而对桥梁挡风屏增速效应引起的接触网正馈线舞动问题鲜有研究.
本文以兰新高铁为研究对象,建立桥梁仿真模型,对比分析无挡风屏和有挡风屏两种形式下接触网正馈线气动特性,同时分析不同的挡风屏高度、挡风屏透风率时正馈线气动特性的差异与规律.
1 计算模型与网格分布
兰新高铁沿线桥梁结构和接触网正馈线是一个复杂的细长结构,同时为了减小模型网格数量,降低计算量和计算时间,本文采用ANSYS有限元软件,基于兰新高铁线路横截面实际尺寸进行二维建模分析.
1.1 模型的选择
由于Transition SST模型在模拟圆柱绕流问题方面可以很好地捕捉到圆柱绕流尾迹近壁区的流动特征,能更好地表现速度、压力梯度、流动分离等变化[16],因此本文湍流模型选择Transition SST模型.速度压力耦合采用SIMPLEC算法,时间步长0.005 s,计算1 000步,仿真时间为5 s.
定义升力系数为

1.2 网格分布
兰新高铁线路挡风屏高4.0 m,宽0.08 m,正馈线高7.2 m,正馈线距挡风屏内侧水平距离1.05 m.因本文以正馈线为研究对象,所以在保证正馈线(关注区)网格数量的前提下,尽量降低非关注区网格密度,进而减少无关网络,网格总数约为100万个.桥梁模型和正馈线周围网格划分如图2~3所示.计算域边界设置:左侧设置为速度入口边界,气流从左向右垂直进入;右侧设置为压力出口边界;正馈线表面设置为无滑移壁面边界.
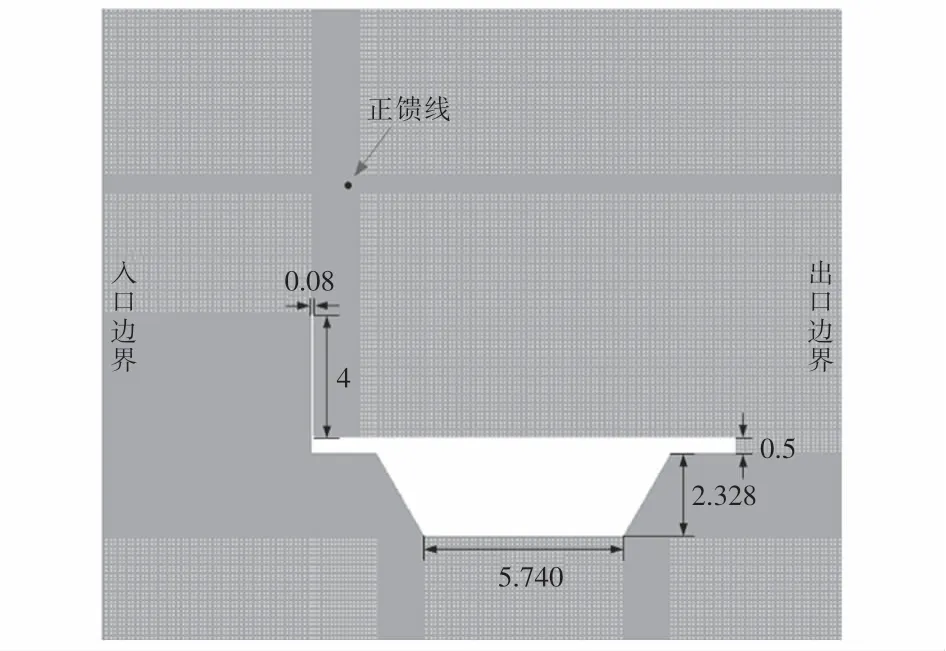
图2 桥梁计算域网格示意图(单位:m)Fig.2 Computational domain grid of bridge(unit:m)
2 风洞试验与仿真验证
基于相似原理设计制作风洞试验装置,对挡风墙后方正馈线处的风速进行测量.建立与风洞试验装置相同尺寸的模型进行仿真分析,对比并验证正馈线气动特性时流体仿真方法的正确性与可行性[17-19].建立的风洞模型为典型的开路式风洞,由风机、大开角段、稳定段、收缩段、实验段以及扩散段几部分组成,风洞试验装置如图4所示.

图3 正馈线周围计算域网格示意图Fig.3 Computing domain grid around positive feeder

图4 风洞试验装置Fig.4 Wind tunnel test device
在试验中需要测量挡风墙后方正馈线处的实际风速,因此需考虑整体模型的几何相似,即考虑挡风墙和接触网正馈线的相似设计.考虑到风洞实验段的大小等条件限制,最终按照1∶59的几何相似比设计并制作实验段模型(见图5).图6为风速测量仪,用于测量实验过程中正馈线处风速.

图5 风洞实验段模型Fig.5 Wind tunnel test section model

图6 风速测量仪Fig.6 Anemometer
对比表1中试验与仿真数据可知:试验结果与仿真结果存在一定的误差,且相对误差随着入口风速的增大而逐渐增大,考虑到试验装置的气密性及其他因素,该误差在允许范围内,且试验结果与仿真结果所获得的风速均为入口风速的2倍左右,说明了该流体仿真方法能够反映出实际中挡风墙对气流的影响效果,验证了本文中求解正馈线气动特性流体仿真方法的正确性与可行性.
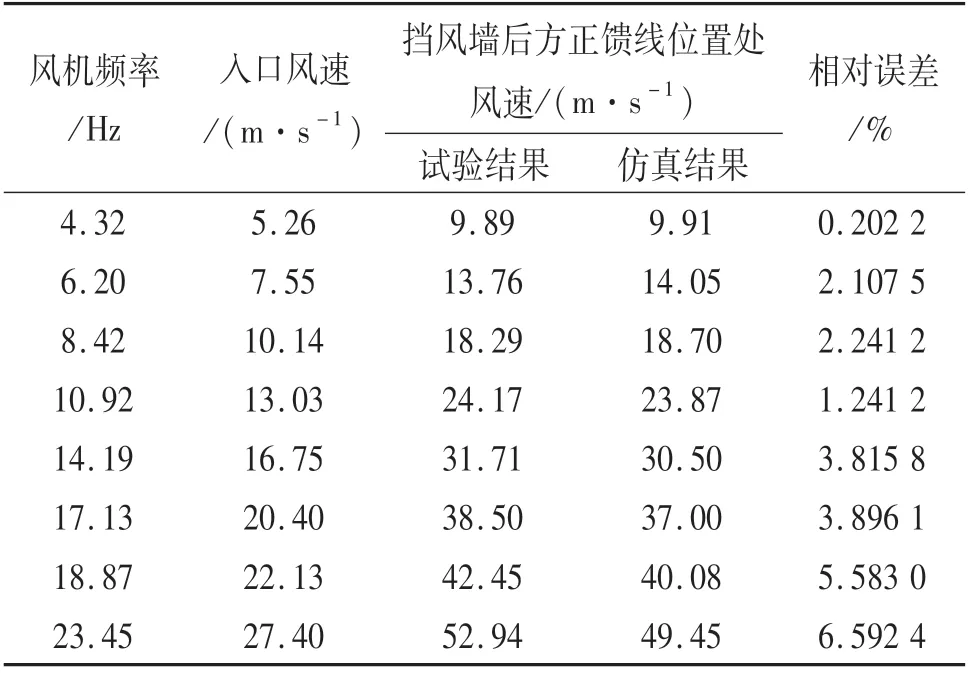
表1 缩尺模型下正馈线处风速试验与仿真结果对比Tab.1 Comparison of wind speed test and simulation results at positive feeder under scale model
3 挡风屏对接触网正馈线的影响
3.1 挡风屏对正馈线的影响
桥梁上多采用较轻薄的挡风屏结构,挡风屏高4.0 m,宽0.08 m,由于挡风屏对来流的增速效应影响,横风在流经桥梁时会形成分布不均匀的漩涡结构.风速为1 m/s及15 m/s时无挡风屏和有挡风屏条件下速度云图如图7~8所示.
对比图7~8可以看出:桥梁无挡风屏时来流紧贴桥梁表面通过,正馈线后方出现卡门涡街现象,漩涡呈现上下交替脱落;桥梁设置挡风屏后,来流受到挡风屏的阻碍作用不再紧贴桥梁表面通过,而是从挡风屏上方通过,并在其后方形成增速区域,正馈线正好位于增速区域内,同时正馈线后方卡门涡街现象逐渐消失.
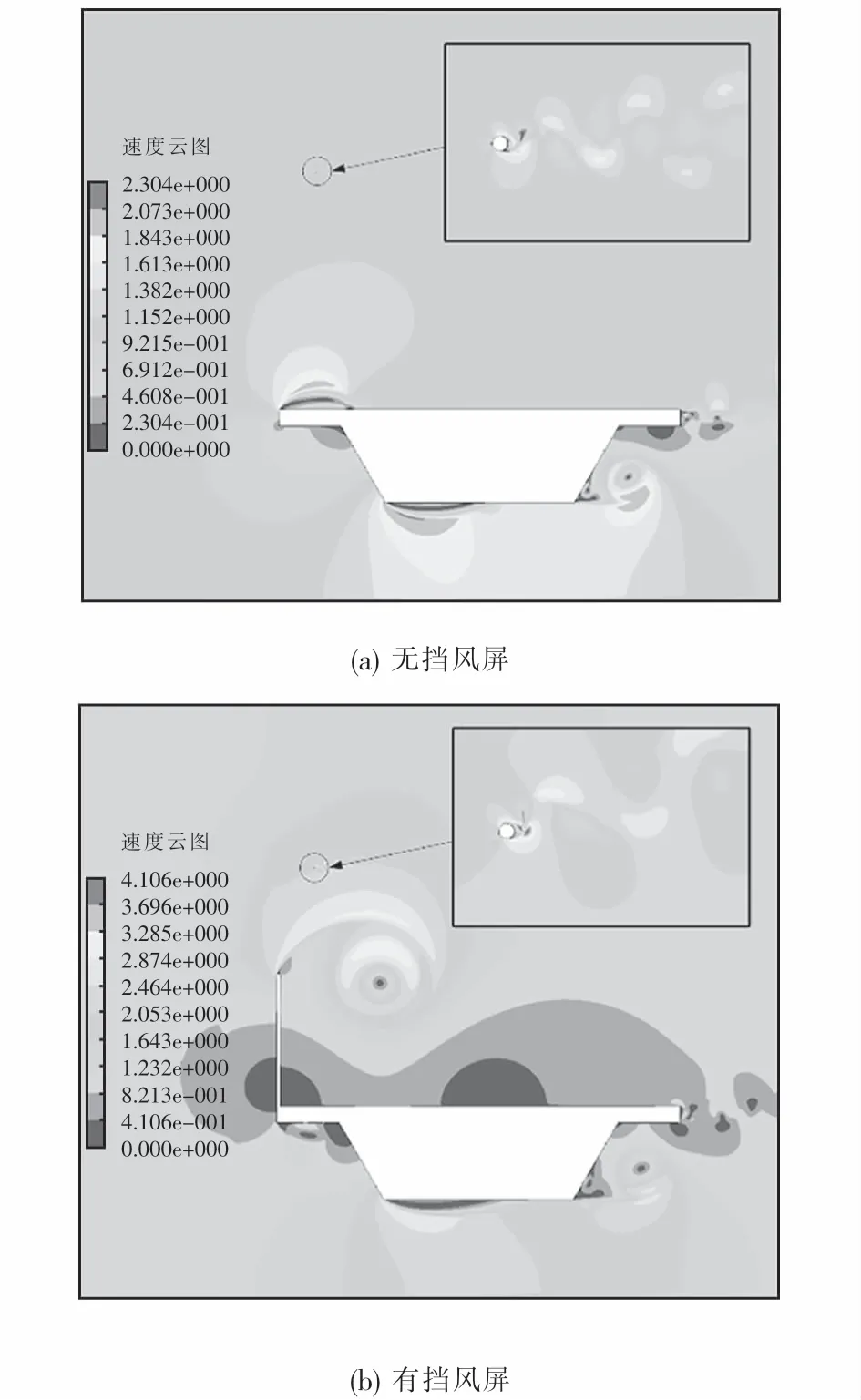
图7 风速1 m/s时桥梁速度云图(单位:m·s-1)Fig.7 Velocity contour of bridge at the wind speed of 1 m/s(unit:m·s-1)
为了充分研究挡风屏结构对正馈线气动性能的影响,分别对无挡风屏和4.0 m高挡风屏结构在风速1,5,10,15,20,25及30 m/s条件下进行仿真计算,得到1 m/s风速和15 m/s风速时无挡风屏和4.0 m高挡风屏条件下升、阻力时程如图9~10所示.
通过对比图9~10可知:风速1 m/s、桥梁无挡风屏时接触网正馈线气动升力系数在-3~3之间交替变化,正馈线阻力系数在2附近交替变化;同风速下桥梁有挡风屏时接触网正馈线气动升力系数在-10~15之间交替变化,正馈线阻力系数增大至3~10之间.风速15 m/s、桥梁无挡风屏时接触网正馈线气动升力系数变化区间为-6~6,阻力系数变化范围为0~4之间;同风速下桥梁有挡风屏时接触网正馈线气动升力系数变化区间为-10~20,阻力系数变化范围为-5~20之间.因此桥梁挡风屏的存在增大了接触网正馈线气动升力系数和阻力系数,加剧了正馈线舞动现象的发生.
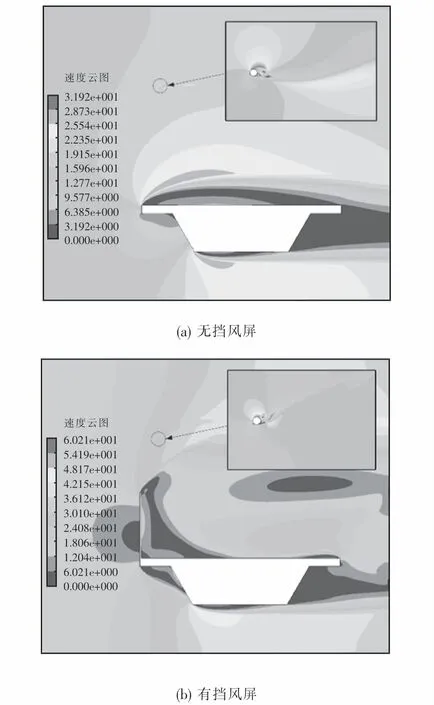
图8 风速15 m/s时桥梁速度云图(单位:m·s-1)Fig.8 Velocity contour of bridge at the wind speed of 15 m/s(unit:m·s-1)
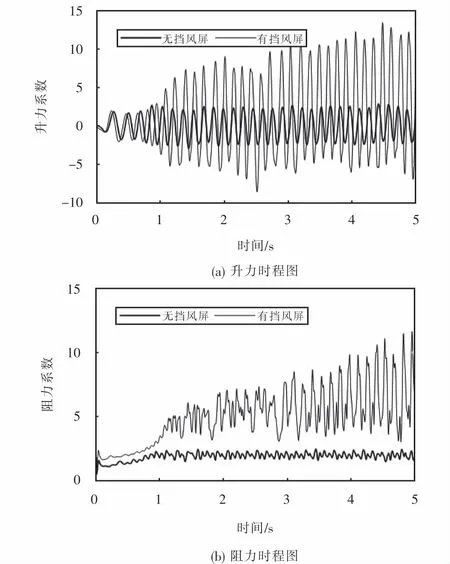
图9 风速1 m/s时正馈线升、阻力时程图Fig.9 Time history of positive feeder lift and drag coefficient at the wind speed of 1 m/s
由于接触网正馈线升力时程曲线呈正负交替变化,故采用均方根值计算,而正馈线阻力时程曲线位于正值部分居多,故采用平均值计算.不同风速时桥梁无挡风屏和有挡风屏条件下的正馈线升力、阻力系数变化曲线如图11所示.
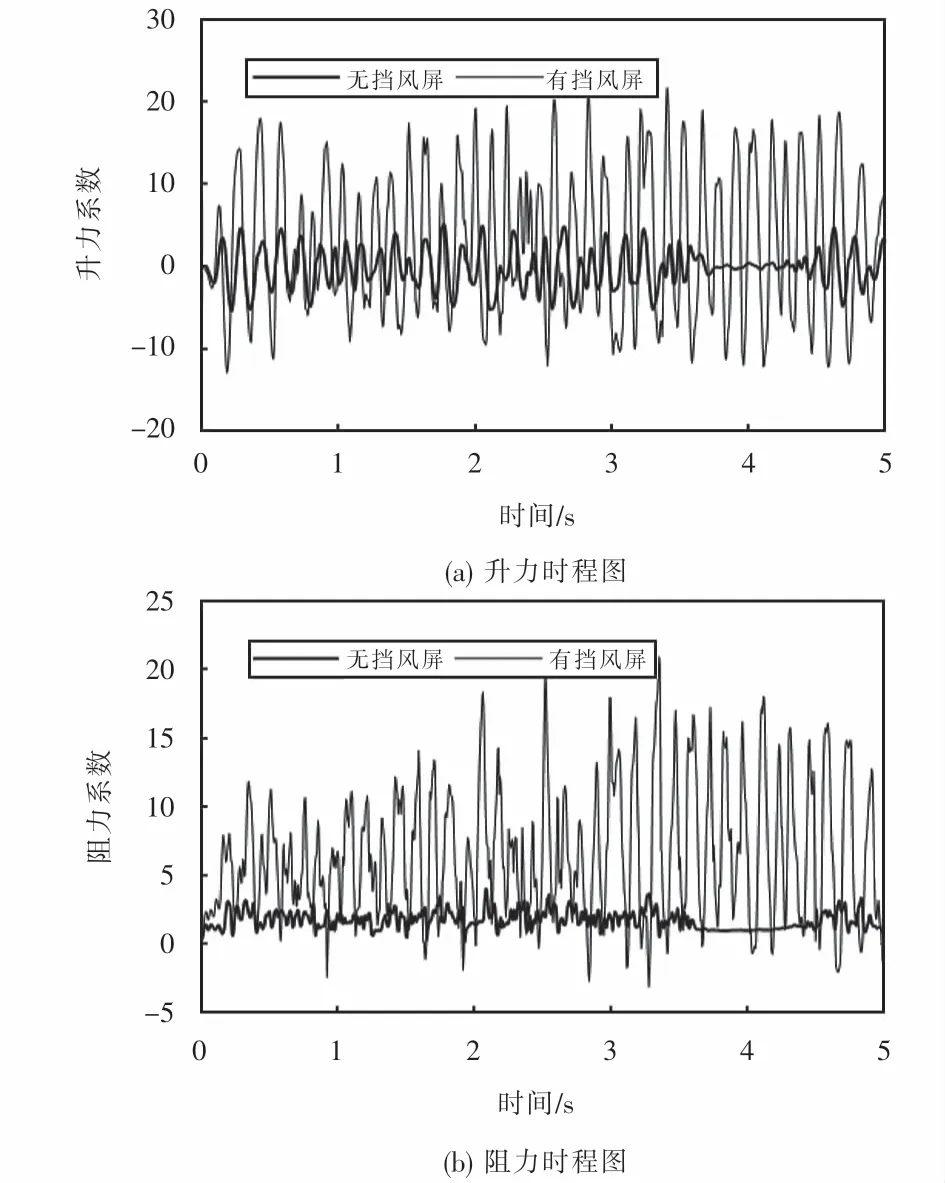
图10 风速15 m/s时正馈线升、阻力时程图Fig.10 Time history of positive feeder lift and drag coefficient at the wind speed of 15 m/s
由图11可知:正馈线气动升力系数最大倍数为15 m/s风速时的3.84倍,最小倍数为5 m/s风速时的2.99倍;同理正馈线气动阻力系数最大倍数为25 m/s风速时的3.81倍,最小倍数为1 m/s风速时的2.62倍.可见在入口风速相同时,无论是正馈线的气动升力系数还是气动阻力系数,都是有挡风屏条件下比无挡风屏条件下的数值大,进一步表明挡风屏的存在对正馈线气动力的变化有着较大的影响.
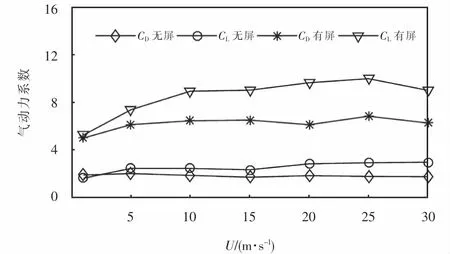
图11 无挡风屏和有挡风屏条件下的气动力系数Fig.11 Aerodynamic coefficients without and with windshield
3.2 挡风屏高度对正馈线的影响
为进一步研究分析挡风屏高度对正馈线气动特性的影响规律,选取高度为2.5,3.0,3.5,4.0及4.5 m五种挡风屏结构,分别在风速15 m/s条件下进行气动性能仿真计算,仿真结果如图12所示.
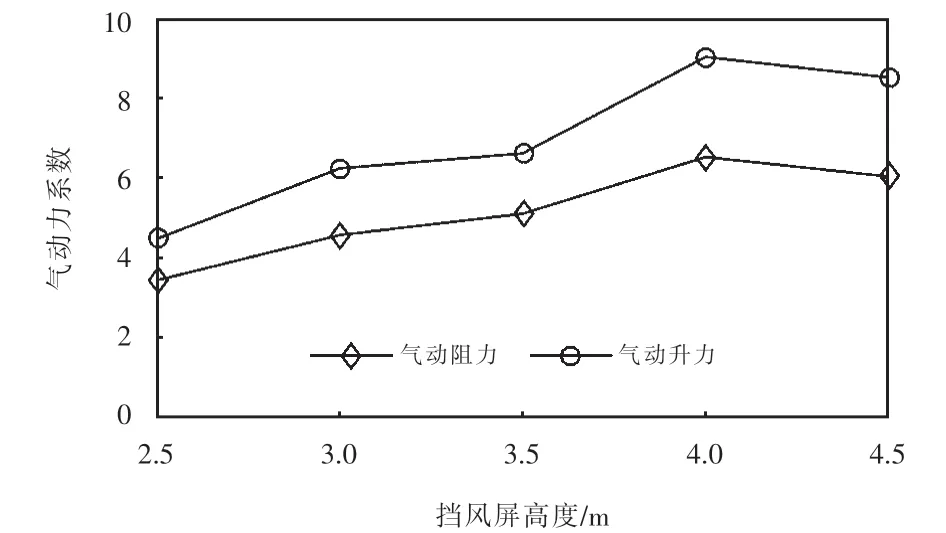
图12 挡风屏不同高度时正馈线气动力系数Fig.12 Aerodynamic coefficient of positive feeder at different heights of windshield
从图12可以看出:随着桥梁挡风屏高度的增加,正馈线的气动升、阻力系数均呈现先增大后减小的趋势,并在挡风屏高度为4 m时达到最大值,此时的正馈线升力系数是2.5 m高挡风屏时的2.01倍,正馈线阻力系数是2.5 m高挡风屏时的1.90倍;当挡风屏高度从2.5 m升高到3.5 m时,正馈线升力系数和阻力系数增加较少;而当挡风屏高度从3.5 m继续增加到4 m的过程中,升力系数和阻力系数变化较大.综合考虑列车与正馈线可知[20],挡风屏高度小于3.5 m时对接触网正馈线气动特性的影响较小.
3.3 挡风屏透风率对正馈线的影响
为了研究分析挡风屏透风率对接触网正馈线气动特性的影响,图13给出了挡风屏高度为4.0 m时,设置4种不同透风率时的模型示意图.通过仿真可以得到风速为15 m/s,透风率分别为30%,40%,50%,60%时正馈线速度云图,如图14所示.
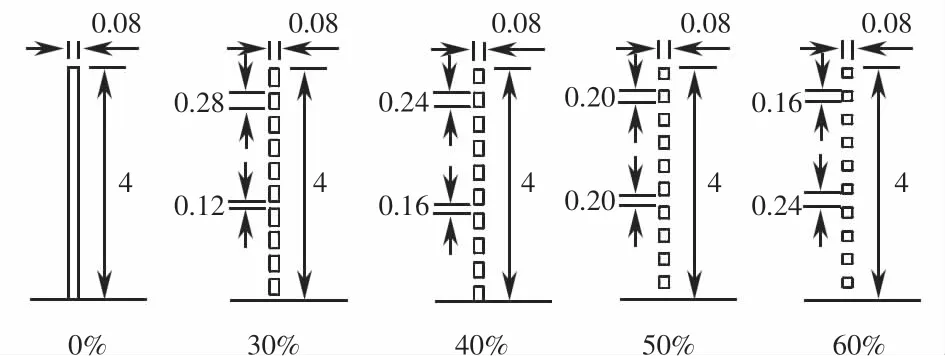
图13 挡风屏透风率模型示意图(单位:m)Fig.13 Schematic diagram of windshield ventilation rate model(unit:m)
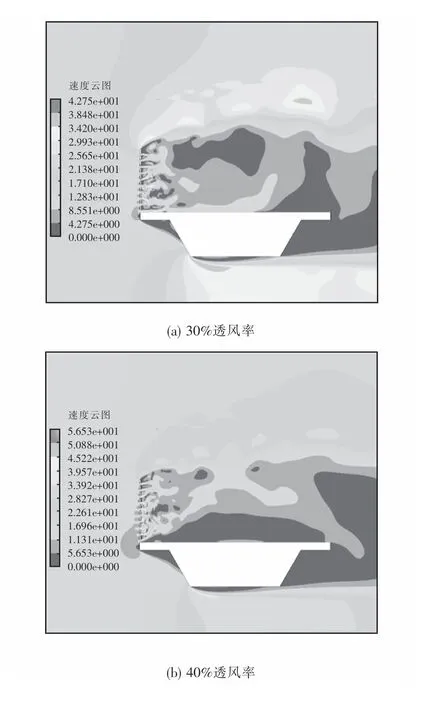
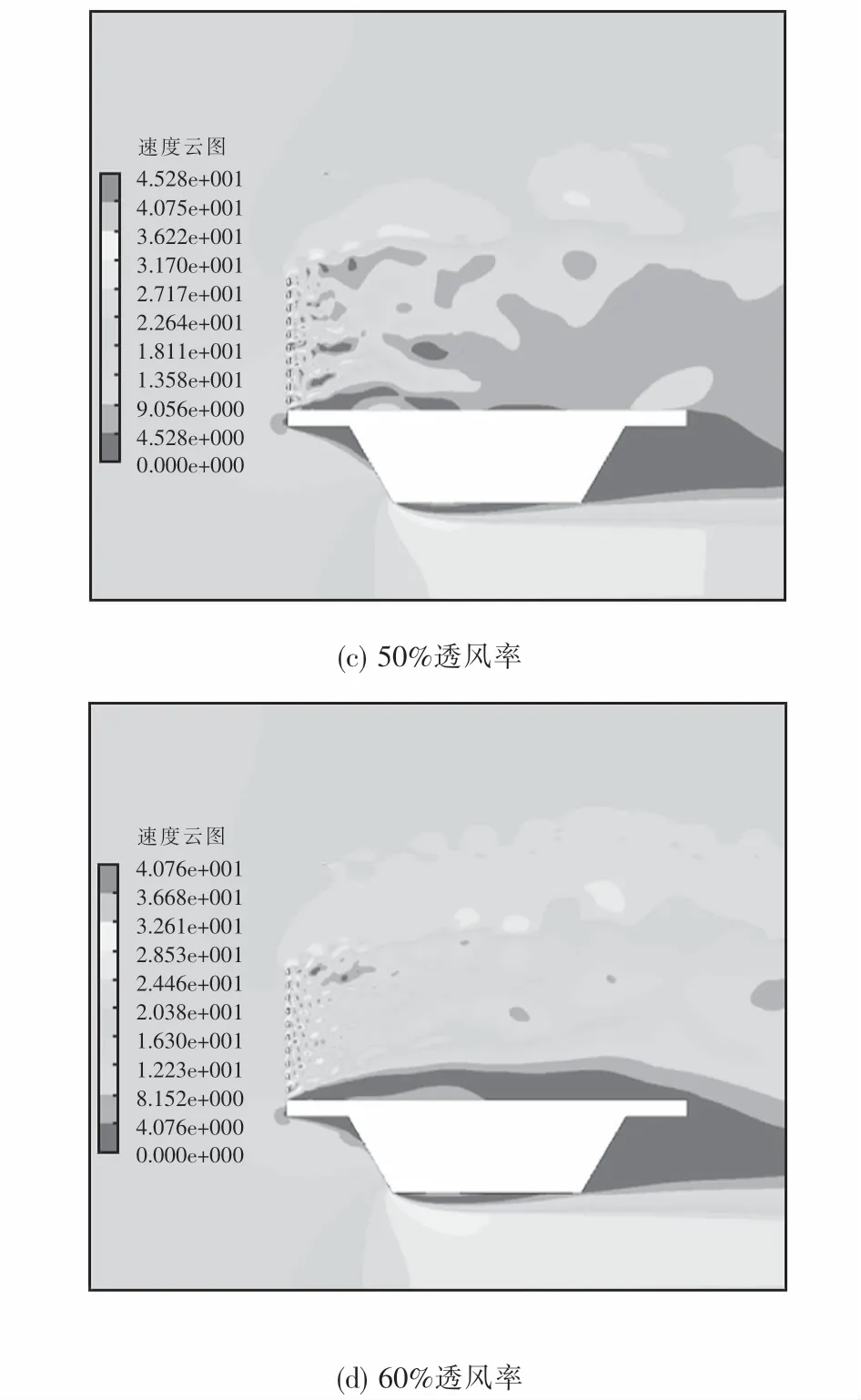
图14 挡风屏不同透风率时桥梁速度云图(单位:m·s-1)Fig.14 Velocity contour of bridge with different ventilation rate(unit:m·s-1)
通过图14可以看出:相较于未设置透风结构的挡风屏,具有透风效果的挡风屏在一定程度上减小了挡风屏对来流的阻碍作用,使更多来流从挡风屏透风结构中穿过,同时,挡风屏透风率越大气流通过挡风屏越多,气流对位于挡风屏后方的影响越大,而对位于上方的正馈线的影响则越小,减少了接触网正馈线舞动的发生.入口风速不同时,正馈线升力系数、阻力系数在不同透风率挡风屏作用下的变化状况如图15~16所示.
通过图15~16可以明显看出:当入口风速不同时,挡风屏透风率为0%时的正馈线升力系数和阻力系数均明显大于其它透风率时的升力系数和阻力系数;同时,挡风屏透风率越小,正馈线升力系数和阻力系数越大;挡风屏透风率越大,正馈线升力系数和阻力系数越小.这也证明在保持挡风屏高度不变的情况下,挡风屏透风率这一因素减小了正馈线所受的气动力,因此应该控制挡风屏的透风率以保证透风效果.通过对比30%~60%透风率下正馈线的升力、阻力系数可以看出:40%的挡风屏透风率在不同风速下具有很好地降低正馈线气动升力、阻力的效果.
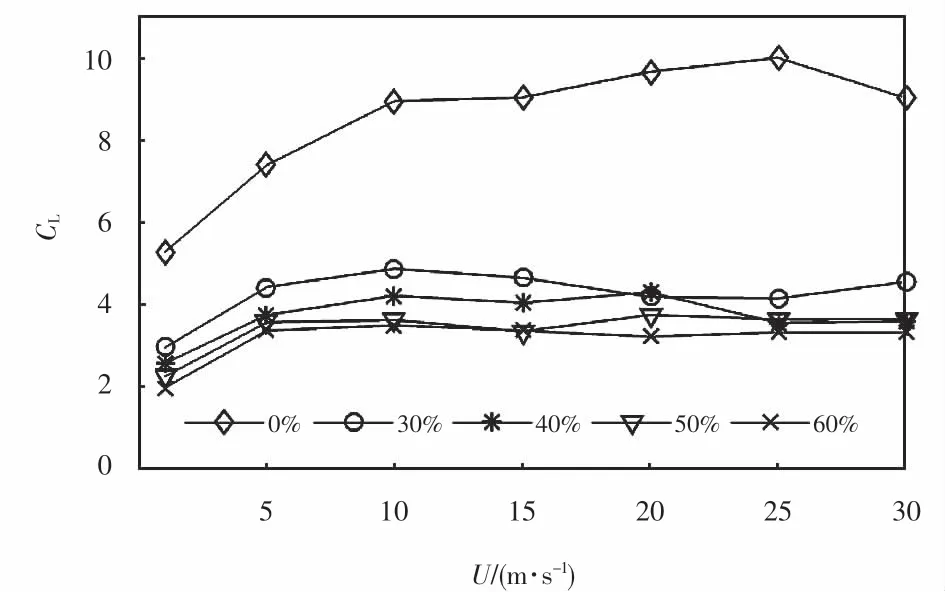
图15 不同透风率时正馈线升力系数变化Fig.15 Coefficient of the lift of the positive feeder with different ventilation rate
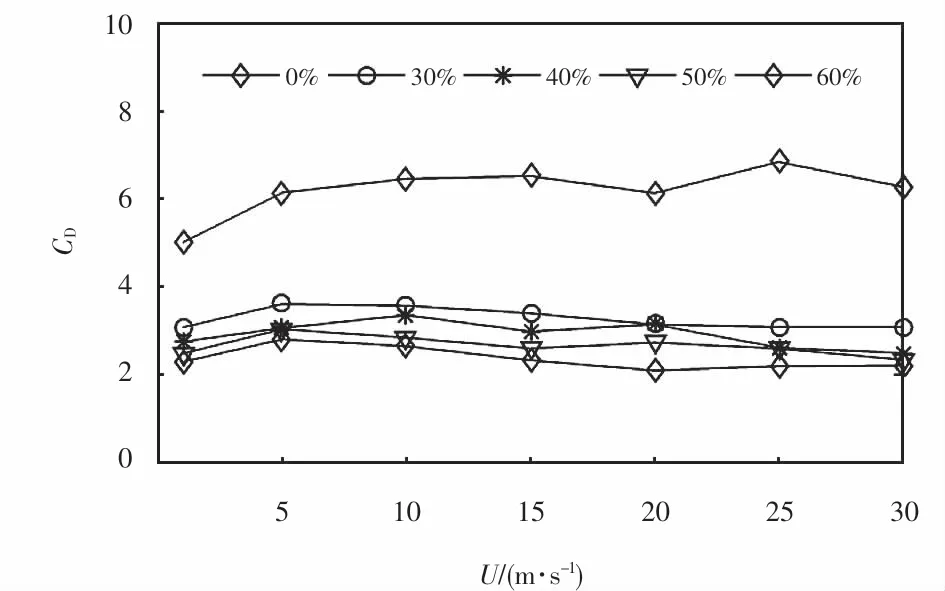
图16 不同透风率时正馈线阻力系数变化Fig.16 Coefficient of the drag of positive feeder with different ventilation rate
4 结论
1)桥梁无挡风屏时,来流紧贴桥梁表面通过对接触网正馈线影响较小;而桥梁设置挡风屏后,来流受到挡风屏的阻碍作用不在紧贴桥面通过,并在其后上方形成增速区域,来流经过挡风屏的增速效应提高了接触网正馈线处风速,造成接触网正馈线舞动现象.
2)在一定范围内桥梁挡风屏设置越高,接触网正馈线升力、阻力系数越大,因此挡风屏高度越低接触网正馈线发生舞动现象的可能性也越低,但列车受到大风的影响越大,故挡风墙高度的设置需综合这两方面的需求合理设置.综合考虑挡风屏高度对列车和正馈线气动性能的影响,挡风屏合理高度设置范围为2.5~3.5 m.
3)桥梁挡风屏无透风结构时,接触网正馈线气动特性明显大于挡风屏设置透风结构时的气动特性;挡风屏透风率越大来流通过越多,接触网正馈线升力系数和阻力系数越小.对比不同挡风屏透风率下正馈线的升力、阻力系数得出,40%的挡风屏透风率在不同风速下具有很好地降低正馈线气动升力、阻力的效果.
